Application Solutions of Plane Elasticity Professor M H

Application Solutions of Plane Elasticity Professor M. H. Sadd

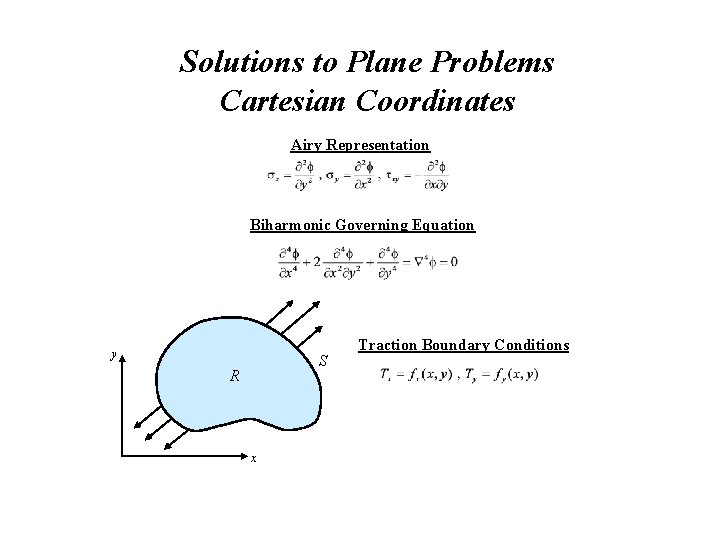
Solutions to Plane Problems Cartesian Coordinates Airy Representation Biharmonic Governing Equation y S R x Traction Boundary Conditions

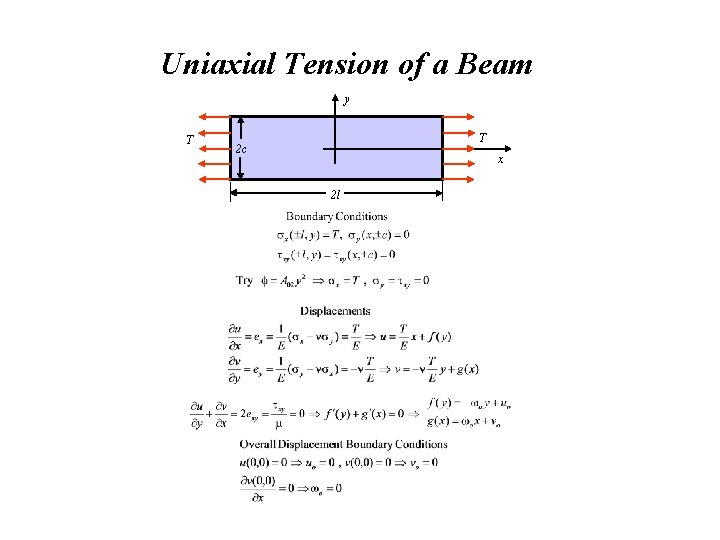
Uniaxial Tension of a Beam y T T 2 c x 2 l

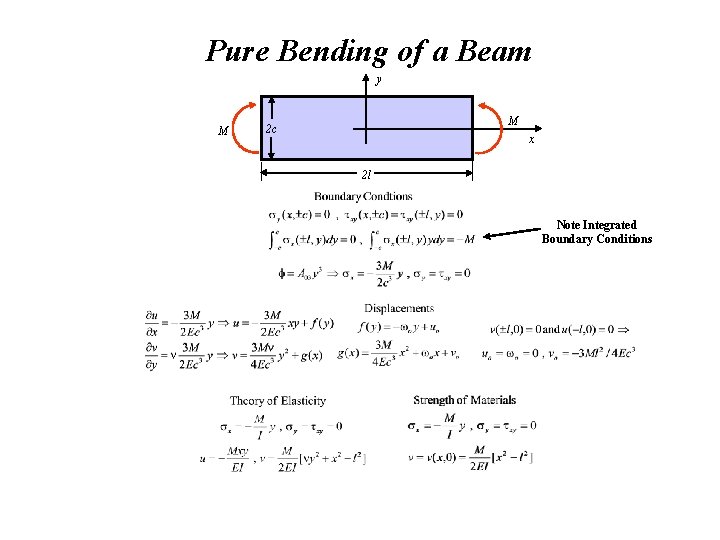
Pure Bending of a Beam y M M 2 c x 2 l Note Integrated Boundary Conditions

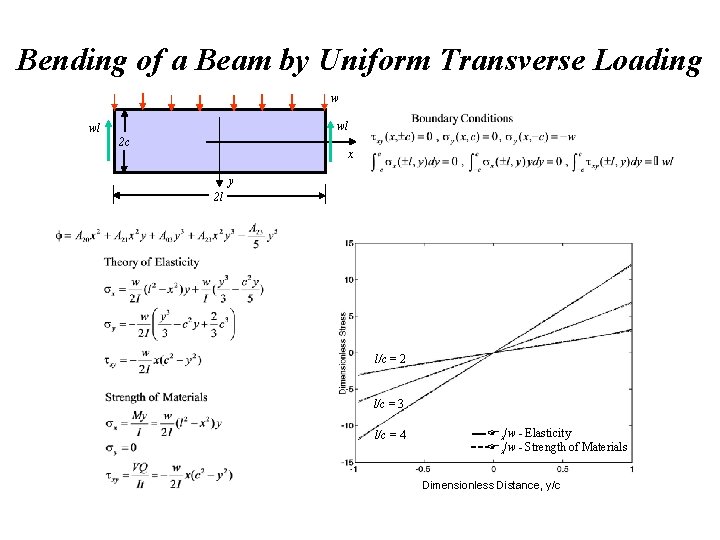
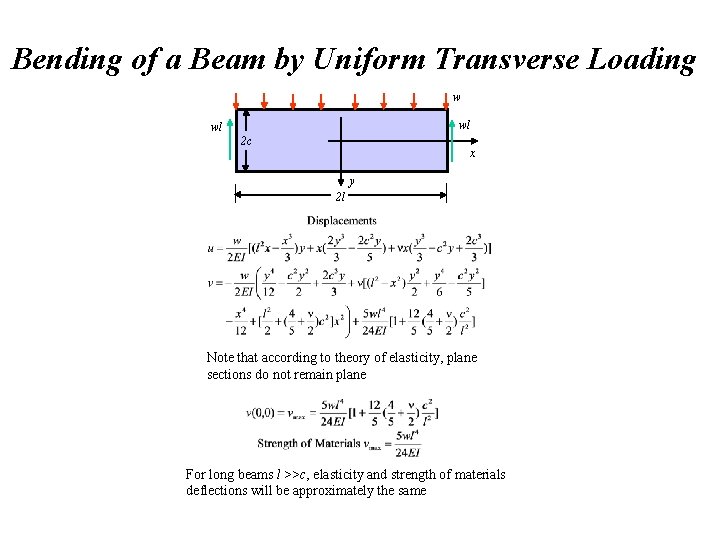
Bending of a Beam by Uniform Transverse Loading w wl wl 2 c x y 2 l l/c = 2 l/c = 3 l/c = 4 x/w - Elasticity x/w - Strength of Materials Dimensionless Distance, y/c

Bending of a Beam by Uniform Transverse Loading w wl wl 2 c x y 2 l Note that according to theory of elasticity, plane sections do not remain plane For long beams l >>c, elasticity and strength of materials deflections will be approximately the same

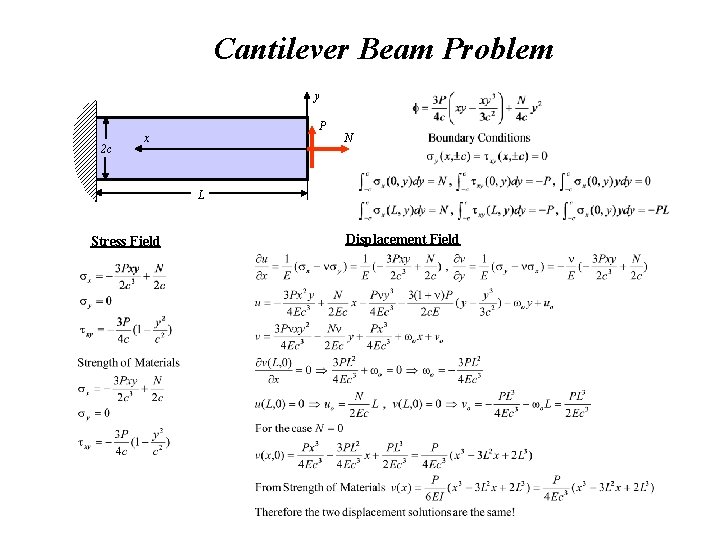
Cantilever Beam Problem y 2 c P x N L Stress Field Displacement Field

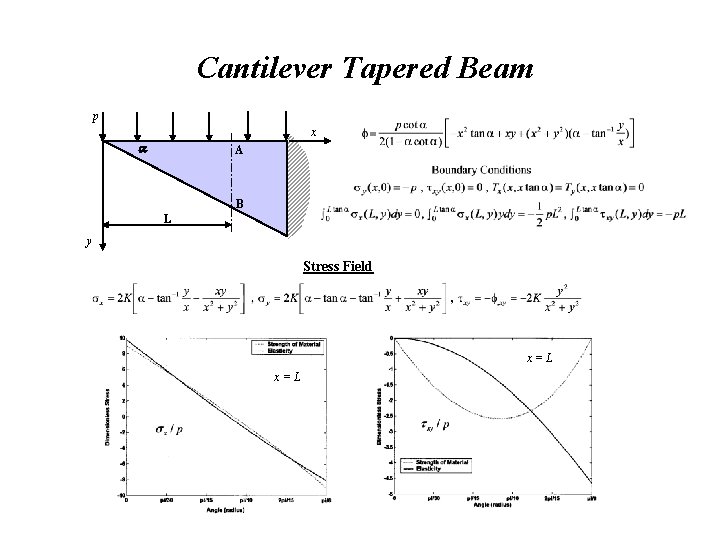
Cantilever Tapered Beam p x A B L y Stress Field x=L

Solutions to Plane Problems Polar Coordinates Airy Representation Biharmonic Governing Equation S R y r x Traction Boundary Conditions

General Solutions in Polar Coordinates

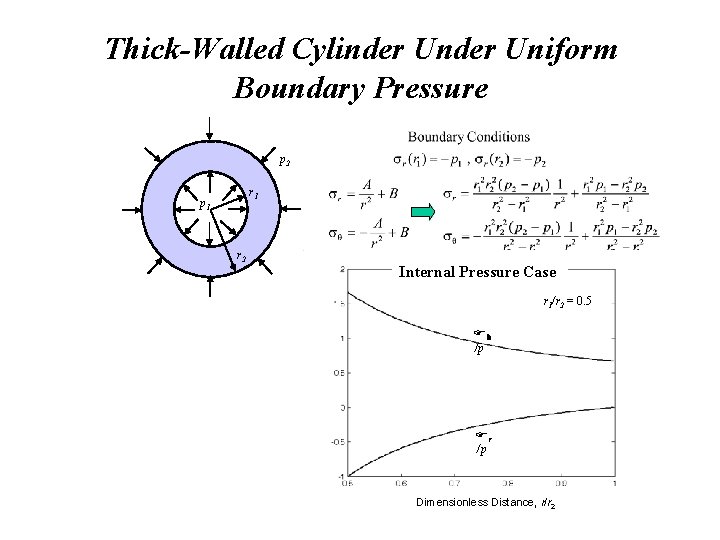
Thick-Walled Cylinder Uniform Boundary Pressure p 2 r 1 p 1 r 2 Internal Pressure Case r 1/r 2 = 0. 5 /p r /p r/r 2 Dimensionless Distance, r/r 2

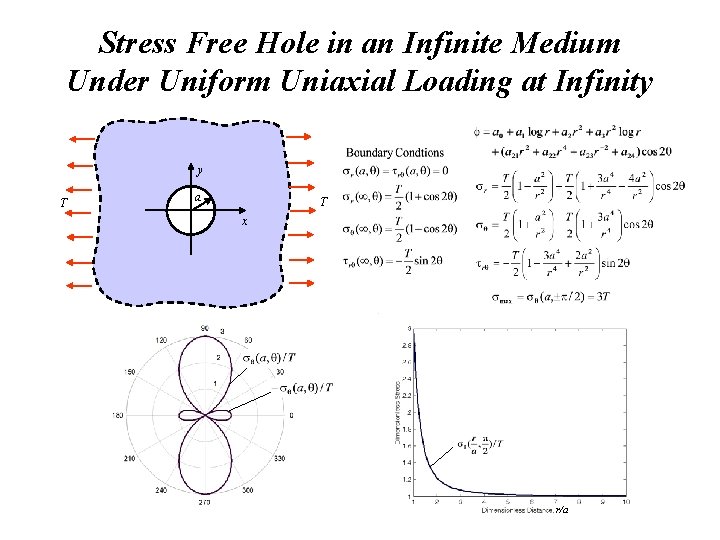
Stress Free Hole in an Infinite Medium Under Uniform Uniaxial Loading at Infinity y T a T x r/a

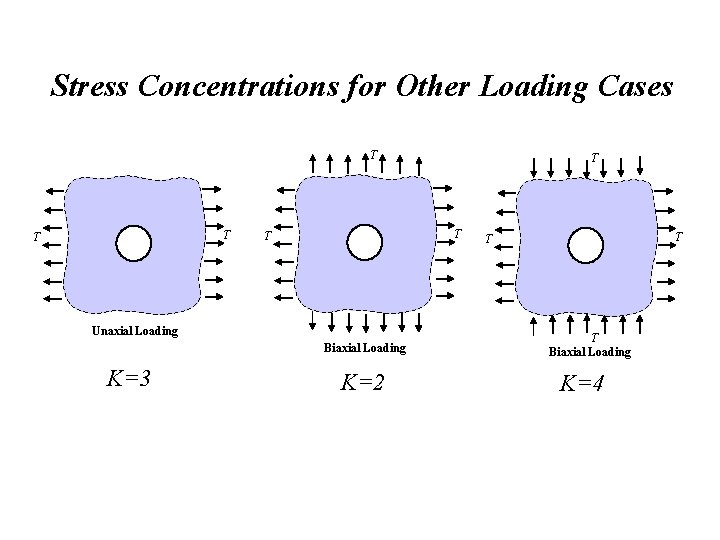
Stress Concentrations for Other Loading Cases T T T Unaxial Loading Biaxial Loading K=3 T K=2 T T T Biaxial Loading K=4

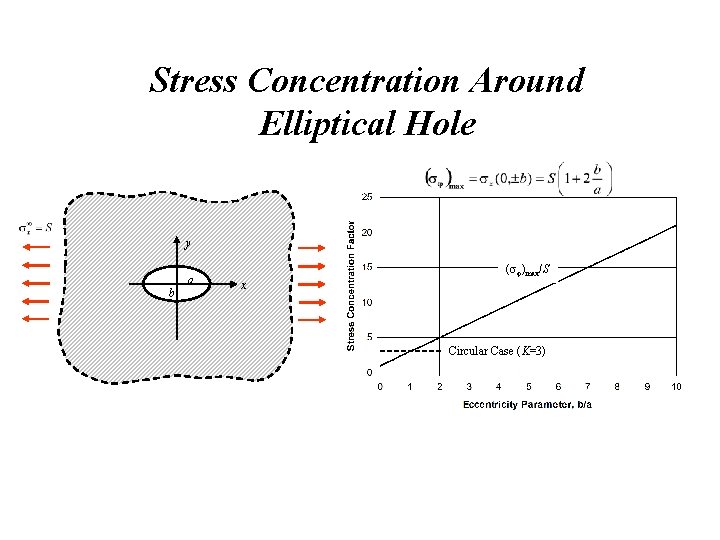
Stress Concentration Around Elliptical Hole y b a ( )max/S x Circular Case (K=3)

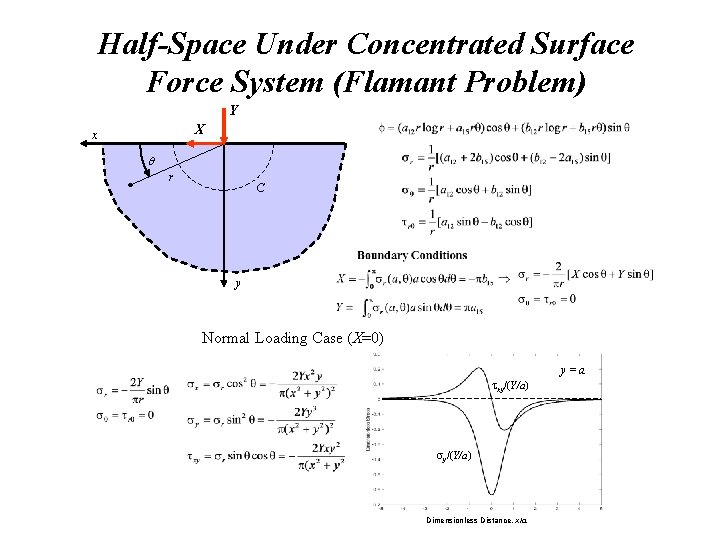
Half-Space Under Concentrated Surface Force System (Flamant Problem) Y X x r C y Normal Loading Case (X=0) y=a xy/(Y/a) Dimensionless Distance, x/a

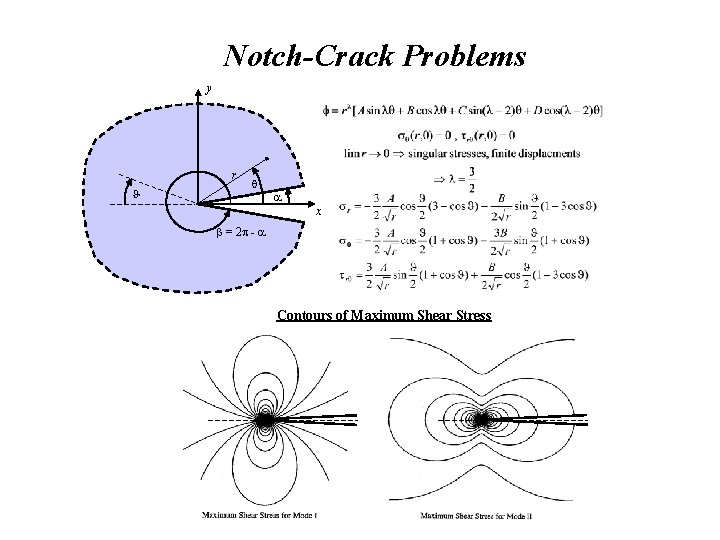
Notch-Crack Problems y r x = 2 - Contours of Maximum Shear Stress

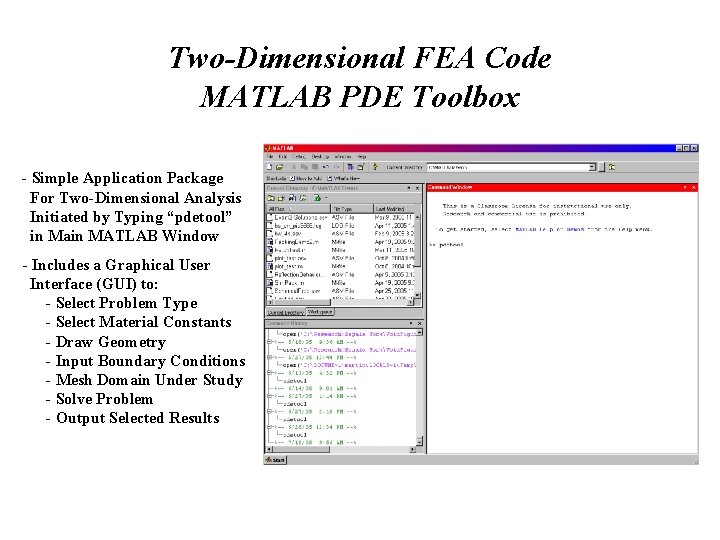
Two-Dimensional FEA Code MATLAB PDE Toolbox - Simple Application Package For Two-Dimensional Analysis Initiated by Typing “pdetool” in Main MATLAB Window - Includes a Graphical User Interface (GUI) to: - Select Problem Type - Select Material Constants - Draw Geometry - Input Boundary Conditions - Mesh Domain Under Study - Solve Problem - Output Selected Results

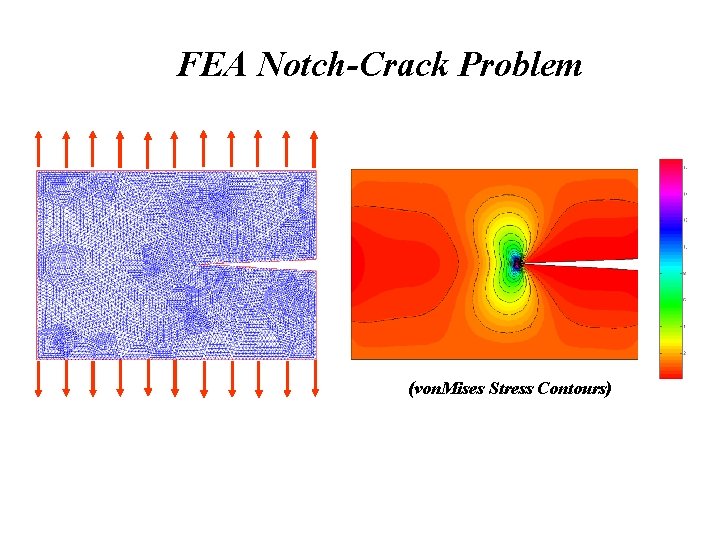
FEA Notch-Crack Problem (von. Mises Stress Contours)

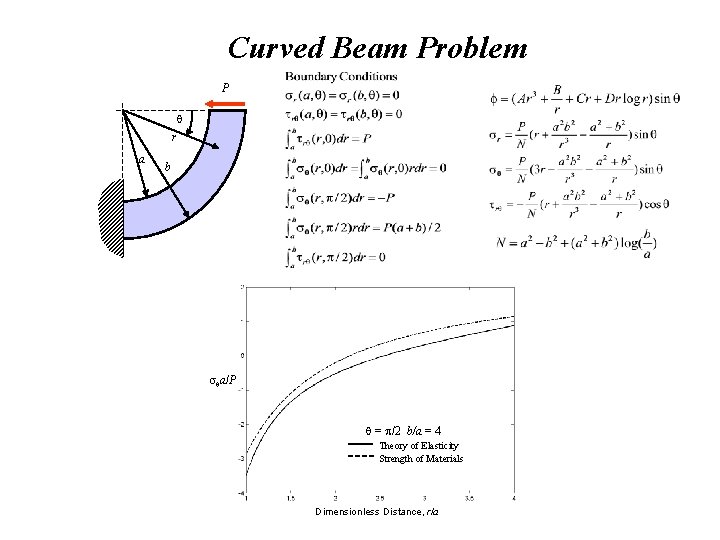
Curved Beam Problem P r a b a/P = /2 b/a = 4 Theory of Elasticity Strength of Materials Dimensionless Distance, r/a

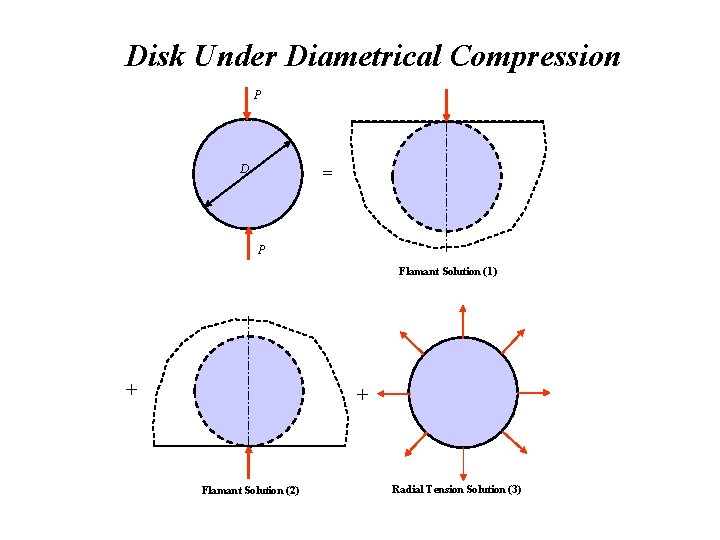
Disk Under Diametrical Compression P = D P Flamant Solution (1) + + Flamant Solution (2) Radial Tension Solution (3)

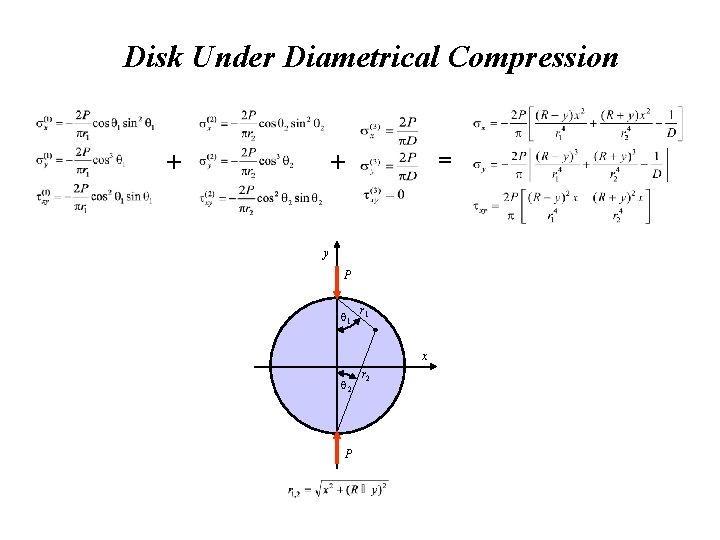
Disk Under Diametrical Compression + = + y P 1 r 1 x 2 P r 2

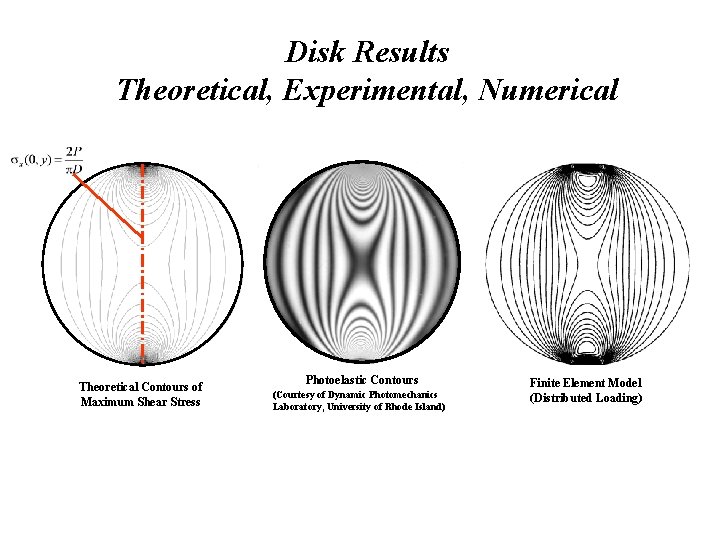
Disk Results Theoretical, Experimental, Numerical Theoretical Contours of Maximum Shear Stress Photoelastic Contours (Courtesy of Dynamic Photomechanics Laboratory, University of Rhode Island) Finite Element Model (Distributed Loading)