APPLICATION of the DFT Estimation of Frequency Spectrum

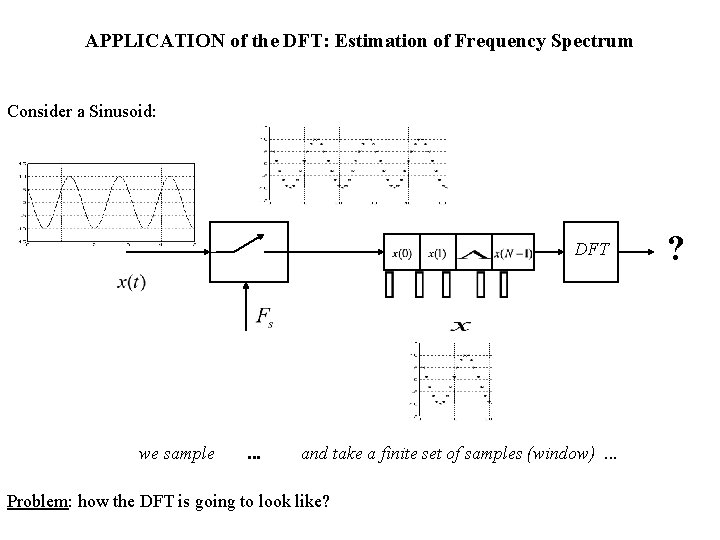
APPLICATION of the DFT: Estimation of Frequency Spectrum Consider a Sinusoid: DFT we sample . . . and take a finite set of samples (window). . . Problem: how the DFT is going to look like? ?

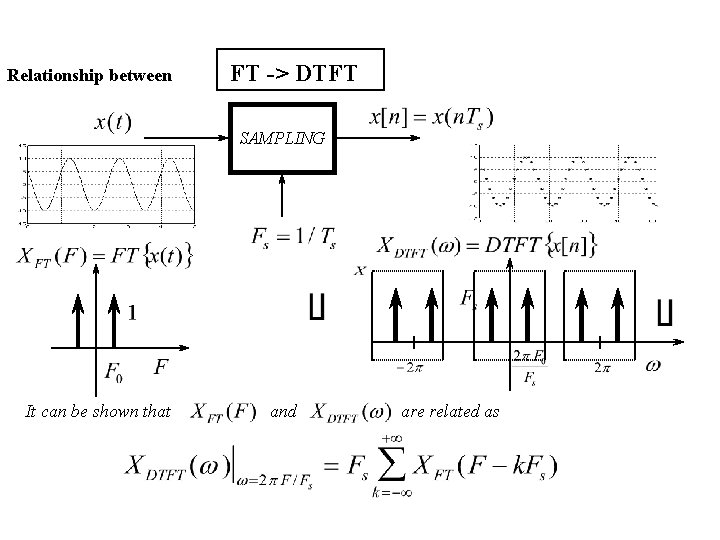
Relationship between FT -> DTFT SAMPLING It can be shown that and are related as

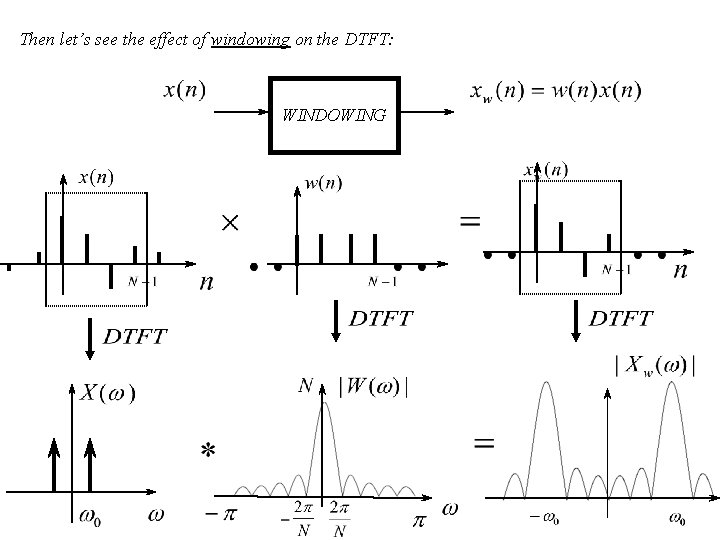
Then let’s see the effect of windowing on the DTFT: WINDOWING

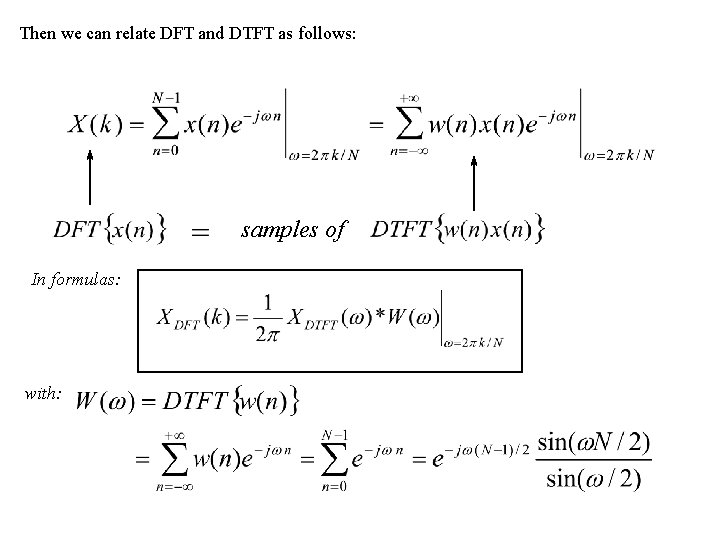
Then we can relate DFT and DTFT as follows: samples of In formulas: with:

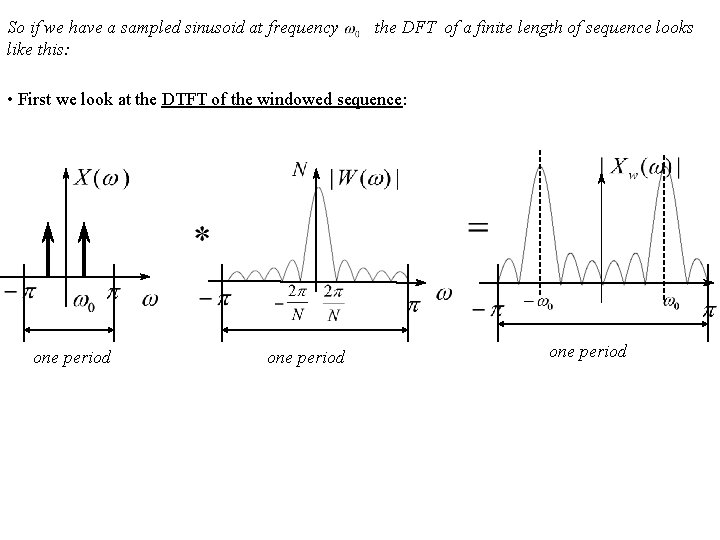
So if we have a sampled sinusoid at frequency like this: the DFT of a finite length of sequence looks • First we look at the DTFT of the windowed sequence: one period

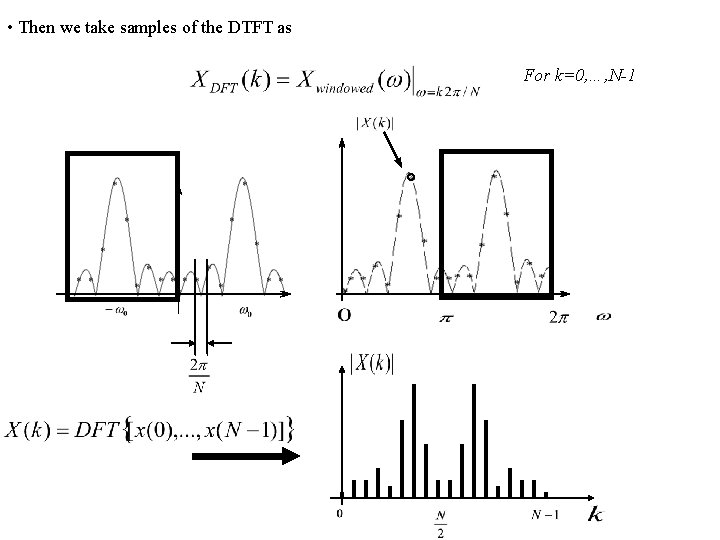
• Then we take samples of the DTFT as For k=0, …, N-1

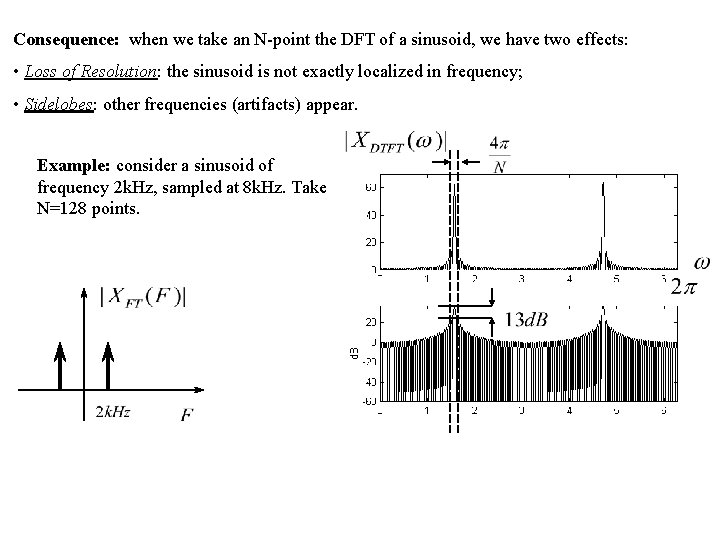
Consequence: when we take an N-point the DFT of a sinusoid, we have two effects: • Loss of Resolution: the sinusoid is not exactly localized in frequency; • Sidelobes: other frequencies (artifacts) appear. Example: consider a sinusoid of frequency 2 k. Hz, sampled at 8 k. Hz. Take N=128 points.

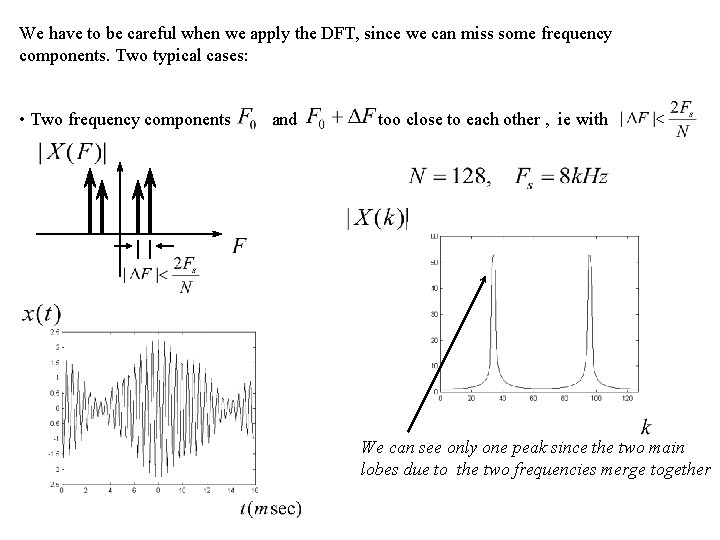
We have to be careful when we apply the DFT, since we can miss some frequency components. Two typical cases: • Two frequency components and too close to each other , ie with We can see only one peak since the two main lobes due to the two frequencies merge together

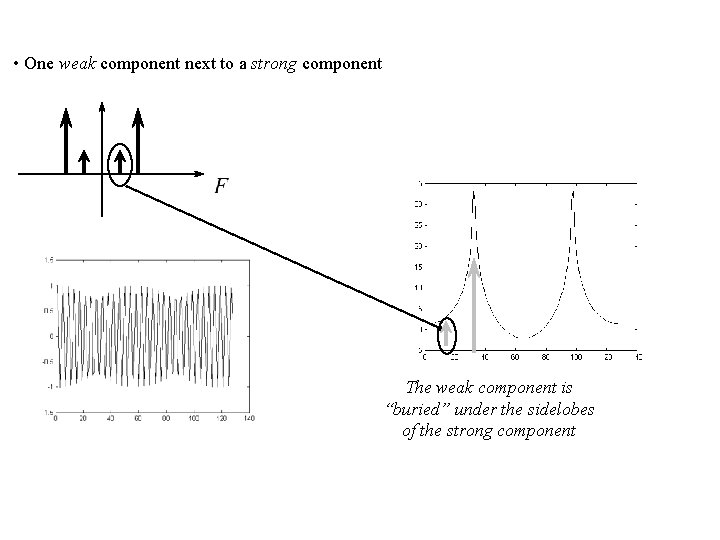
• One weak component next to a strong component The weak component is “buried” under the sidelobes of the strong component

As seen, there are two main problems when we want to estimate the frequency spectrum using the DFT: • Loss of resolution: a peak of the DFT at an index can be anywhere in the interval signifies a sinusoid at a frequency which in digital frequency (radians), or in analog frequency (Hz) To improve the resolution: use more data points! (ie. larger N)

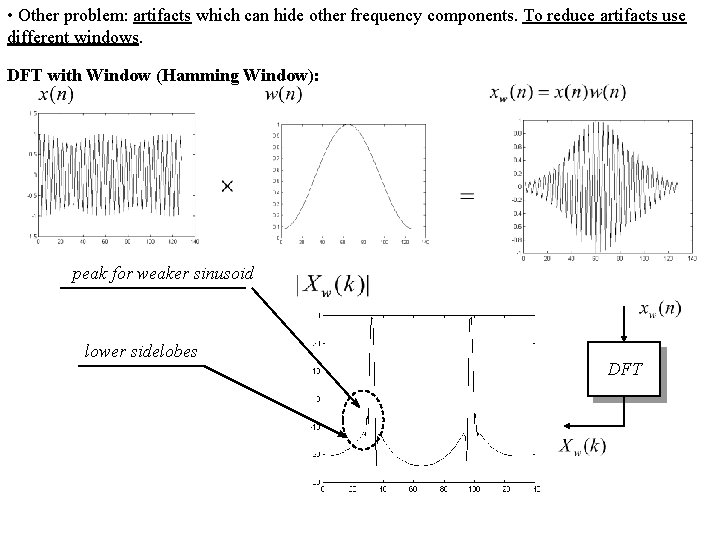
• Other problem: artifacts which can hide other frequency components. To reduce artifacts use different windows. DFT with Window (Hamming Window): peak for weaker sinusoid lower sidelobes DFT

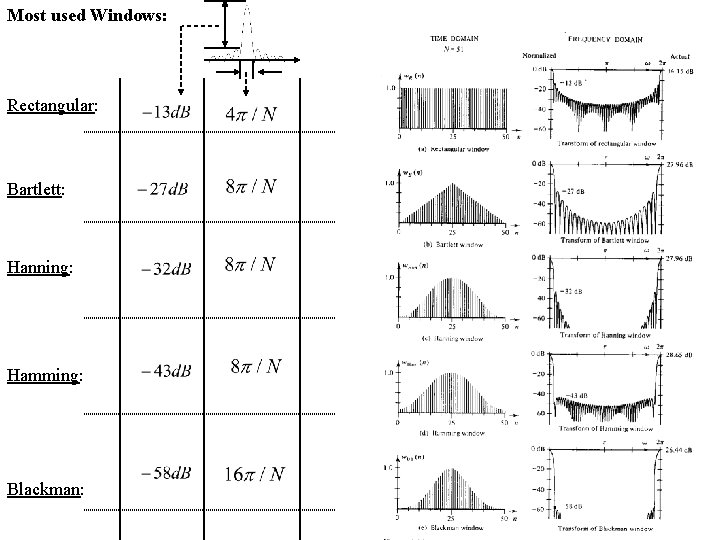
Most used Windows: Rectangular: Bartlett: Hanning: Hamming: Blackman: