Application of quantum universal composability th 1 Motivation

Application of quantum universal composability th 1. Motivation : e. g. is QKD secure? 2. Tool : universal composability 3. Application 1: composability of QKD 4. Application 2: composability of variants of quantum authentication + key recycling

Recitation session for the workshop Unruh’s talk, Renner’s talk 1. Motivation : e. g. is QKD secure? 2. Tool : universal composability Unruh’s talk 3. Application 1: composability of Unruh’s QKD talk, Renner’s talk Oppenheim’s talk 4. Application 2: composability of variants of quantum authentication + key recycling No need to give the talk ! No surprise Too repetitive for some Too brief for others Easier talk since the audience ar well acquainted with the subject Can work through a couple of examples in detail The results are actually complementary ! Give me hints throughout the talk which case it is.

Application of quantum universal composability th 1. Motivation : e. g. is QKD secure? 2. Tool : universal composability 3. Application 1: composability of QKD 4. Application 2: composability of variants of quantum authentication + key recycling

Application of quantum universal composability th 1. Motivation : e. g. is QKD secure? 2. Tool : universal composability 3. Application 1: composability of QKD 4. Application 2: composability of variants of quantum authentication + key recycling Michael Ben-Or 2, 3 Patrick Hayden 4 Michal Horedecki 3 Debbie Leung 3, 4 Dominic Mayers 2, 3, 4 Jonathan Oppenheim 3 MB audience PH DM

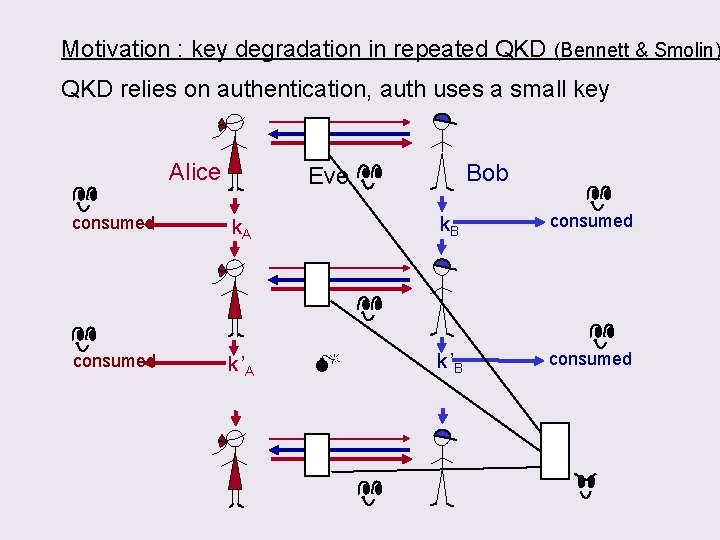
Motivation : key degradation in repeated QKD (Bennett & Smolin) QKD relies on authentication, auth uses a small key Alice Bob Eve consumed k. A consumed k ’A k. B consumed k ’B consumed

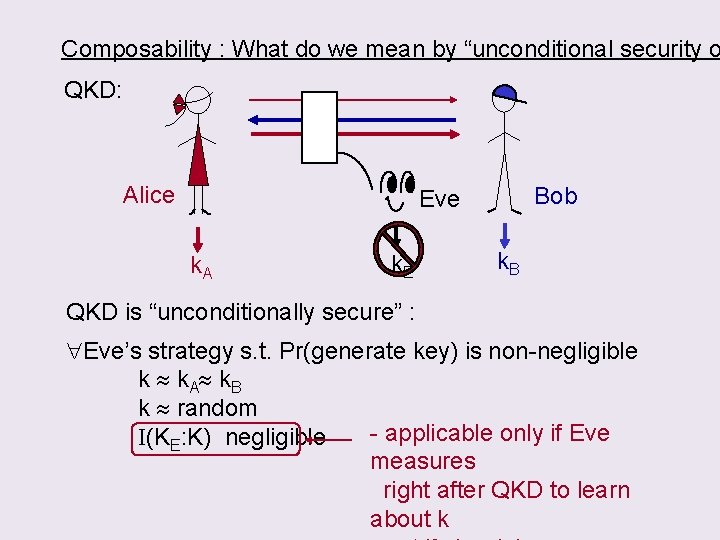
Composability : What do we mean by “unconditional security o QKD: Alice Bob Eve k. A k. E k. B QKD is “unconditionally secure” : Eve’s strategy s. t. Pr(generate key) is non-negligible k k. A k. B k random - applicable only if Eve I(KE: K) negligible measures right after QKD to learn about k

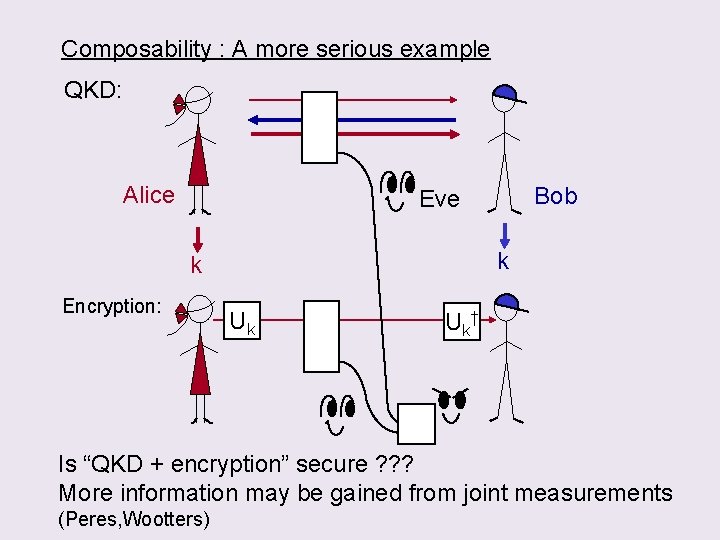
Composability : A more serious example QKD: Alice Bob Eve k k Encryption: Uk U k† Is “QKD + encryption” secure ? ? ? More information may be gained from joint measurements (Peres, Wootters)

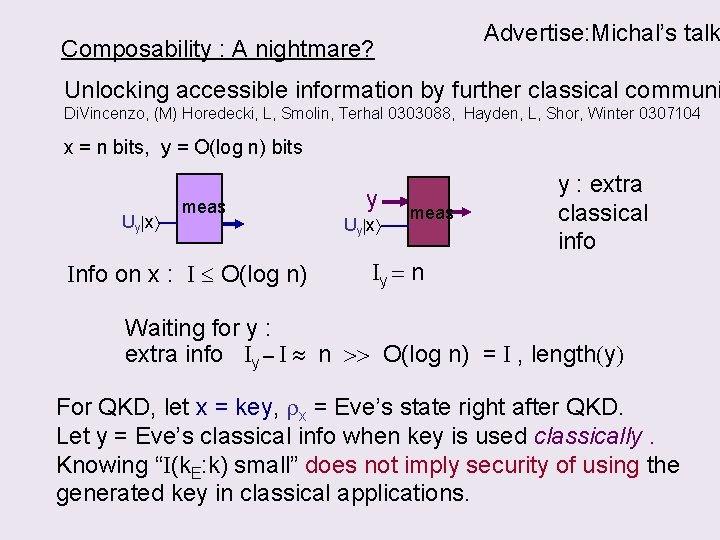
Advertise: Michal’s talk Composability : A nightmare? Unlocking accessible information by further classical communi Di. Vincenzo, (M) Horedecki, L, Smolin, Terhal 0303088, Hayden, L, Shor, Winter 0307104 x = n bits, y = O(log n) bits Uy x meas Info on x : I O(log n) y Uy x meas y : extra classical info Iy = n Waiting for y : extra info Iy – I n >> O(log n) = I , length(y) For QKD, let x = key, rx = Eve’s state right after QKD. Let y = Eve’s classical info when key is used classically. Knowing “I(k. E: k) small” does not imply security of using the generated key in classical applications.

Pre-conclusions : 1. Life can be bad -- be ultra paranoid (about composability) 2. QKD is composable, fortunately (BUT REMEMBER TO USE better security criterion e. g. singlet-fidelity. . . at least until Iacc is “vindicated”, if at all. )

When is a crytographic primitive “safe-to-use”? Wait. . . used in what?

Universal Composability Michael Ben-Or & Dominic Mayers 02 Alternative model by Unruh & Mueller-Quade

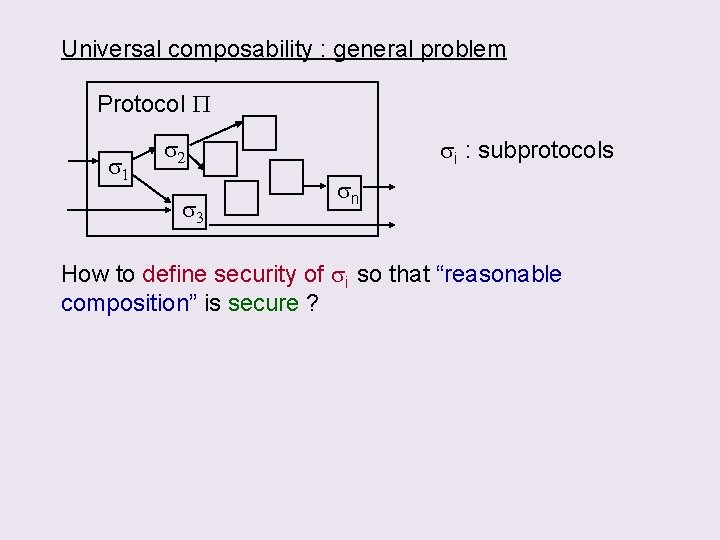
Universal composability : general problem Protocol P s 1 s 2 s 3 si : subprotocols sn How to define security of si so that “reasonable composition” is secure ?

Notations: s : protocol s. I : ideal task attempted by s P+s : protocol calling s as subroutine, trying to perform (imperf. . . s. I P+s. I e. g. PI = perfect encryption, s. I = perfect key distribution, s = Q P+s. I or P+s = encryption with perfect key or QKD key. Wanted : e. g. s, P+s. I, P+s Security definition of protocols should imply secure basic composition P If s. Composable & P+s. I both “secure” then P+s is security definition. Universal “secure” Security definition & security of composition: a pair of related co

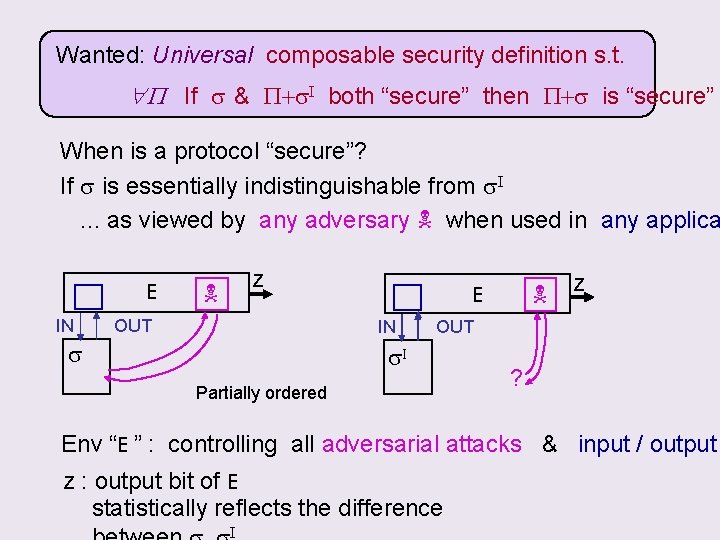
Wanted: Universal composable security definition s. t. P If s & P+s. I both “secure” then P+s is “secure” When is a protocol “secure”? If s is essentially indistinguishable from s. I. . . as viewed by any adversary when used in any applica E IN z OUT IN s E z OUT s. I Partially ordered ? Env “E ” : controlling all adversarial attacks & input / output z : output bit of E statistically reflects the difference I

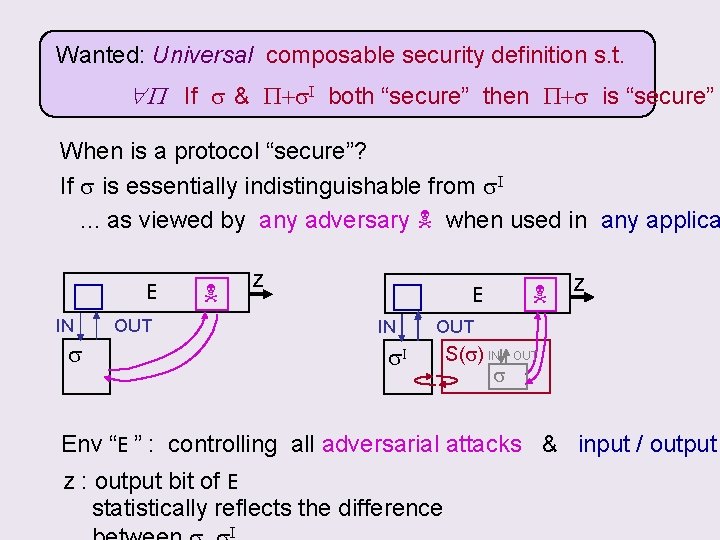
Wanted: Universal composable security definition s. t. P If s & P+s. I both “secure” then P+s is “secure” When is a protocol “secure”? If s is essentially indistinguishable from s. I. . . as viewed by any adversary when used in any applica E IN z OUT E IN s z OUT s. I S(s) IN s OUT Env “E ” : controlling all adversarial attacks & input / output z : output bit of E statistically reflects the difference I

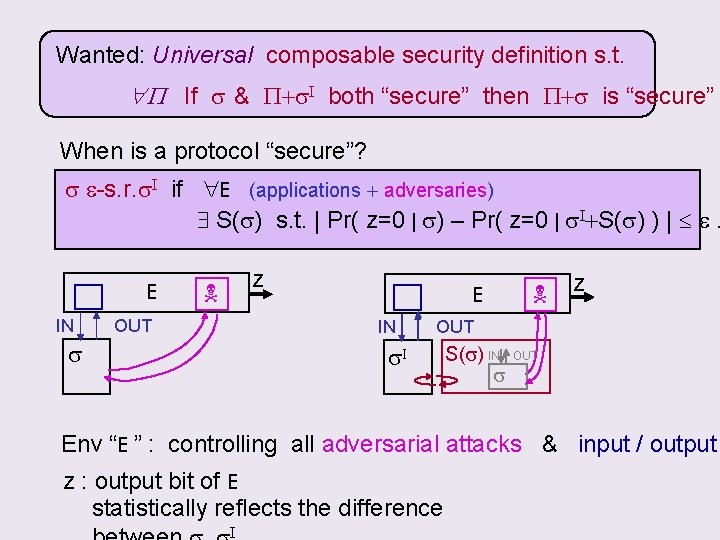
Wanted: Universal composable security definition s. t. P If s & P+s. I both “secure” then P+s is “secure” When is a protocol “secure”? s e-s. r. s. I if E (applications + adversaries) S(s) s. t. | Pr( z=0 | s) – Pr( z=0 | s. I+S(s) ) | e. E IN z OUT E IN s z OUT s. I S(s) IN s OUT Env “E ” : controlling all adversarial attacks & input / output z : output bit of E statistically reflects the difference I

CLAIM: using the following Universal composable security definition s e-s. r. s. I if E (applications + adversaries) S(s) s. t. | Pr( z=0 | s) – Pr( z=0 | s. I+S(s) ) | e. will imply the basic composition P+s. I I eboth “secure” If. If s &P+s PI andthen s e. P+s s. I “secure” P - s. r. s-s. r. is then P+s ( e. P+es ) -s. r. PI.

Universal composable security definition secure basic comp Let P+s be a protocol calling subprotocol s, trying to perform P P+s. I e. P - s. r. PI and s es-s. r. s. I P+s ( e. P+es ) -s. r. PI. If then Proof: E IN P s OUT z

Universal composable security definition secure basic comp Let P+s be a protocol calling subprotocol s, trying to perform P P+s. I e. P - s. r. PI and s es-s. r. s. I P+s ( e. P+es ) -s. r. PI. If then Proof: E IN P s z OUT IN Es E OUT P s. I s es-s. r. s. I Pr(z=0 | P+s) differ by es z Es S(s) Pr(z=0 | P+s. I)

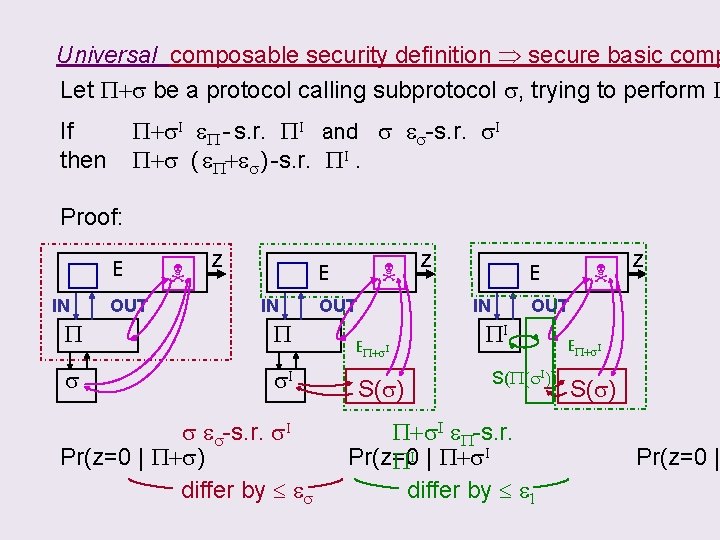
Universal composable security definition secure basic comp Let P+s be a protocol calling subprotocol s, trying to perform P P+s. I e. P - s. r. PI and s es-s. r. s. I P+s ( e. P+es ) -s. r. PI. If then Proof: E IN OUT z E IN P P s s. I s es-s. r. s. I Pr(z=0 | P+s) differ by es OUT z IN EP+s. I S(s) E z OUT PI S(P(s. I)) P+s. I e. P-s. r. Pr(z=0 PI | P+s. I) differ by e 1 EP+s. I S(s) Pr(z=0 |

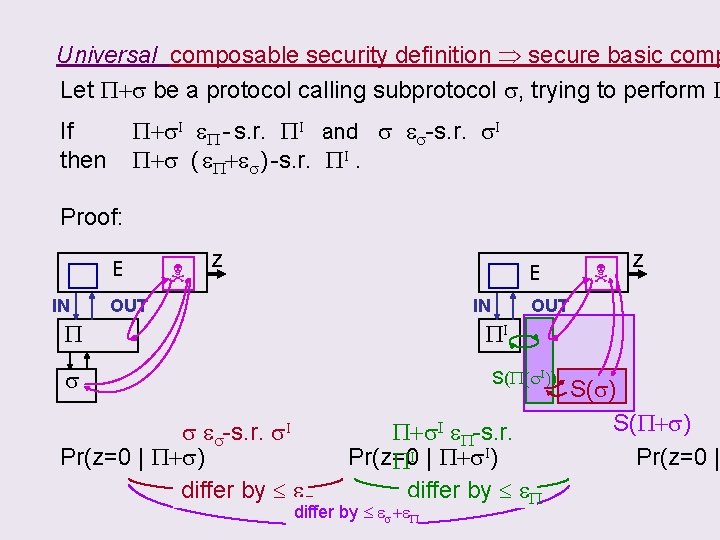
Universal composable security definition secure basic comp Let P+s be a protocol calling subprotocol s, trying to perform P P+s. I e. P - s. r. PI and s es-s. r. s. I P+s ( e. P+es ) -s. r. PI. If then Proof: E IN z E OUT IN P z OUT PI s S(P(s. I)) s es-s. r. s. I Pr(z=0 | P+s) differ by es P+s. I e. P-s. r. Pr(z=0 PI | P+s. I) differ by e. P differ by es+e. P S(s) S(P+s) Pr(z=0 |

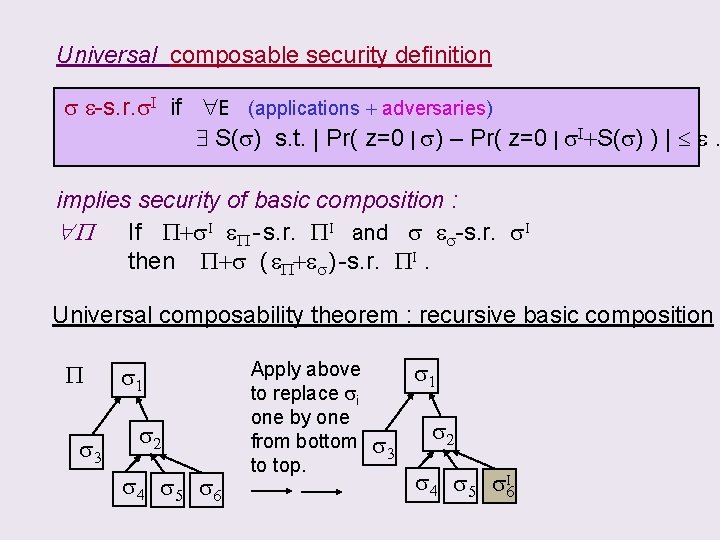
Universal composable security definition s e-s. r. s. I if E (applications + adversaries) S(s) s. t. | Pr( z=0 | s) – Pr( z=0 | s. I+S(s) ) | e. implies security of basic composition : P If P+s. I e. P - s. r. PI and s es-s. r. s. I then P+s ( e. P+es ) -s. r. PI. Universal composability theorem : recursive basic composition P s 3 s 1 s 2 s 4 s 5 s 6 Apply above to replace si one by one from bottom to top. s 1 s 3 s 2 s 4 s 5 s. I 6

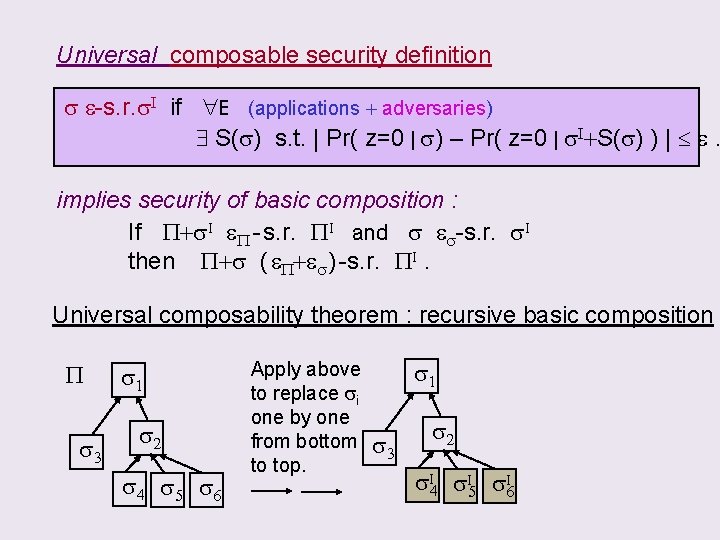
Universal composable security definition s e-s. r. s. I if E (applications + adversaries) S(s) s. t. | Pr( z=0 | s) – Pr( z=0 | s. I+S(s) ) | e. implies security of basic composition : If P+s. I e. P - s. r. PI and s es-s. r. s. I then P+s ( e. P+es ) -s. r. PI. Universal composability theorem : recursive basic composition P s 3 s 1 s 2 s 4 s 5 s 6 Apply above to replace si one by one from bottom to top. s 1 s 3 s 2 s. I 4 s. I 5 s. I 6

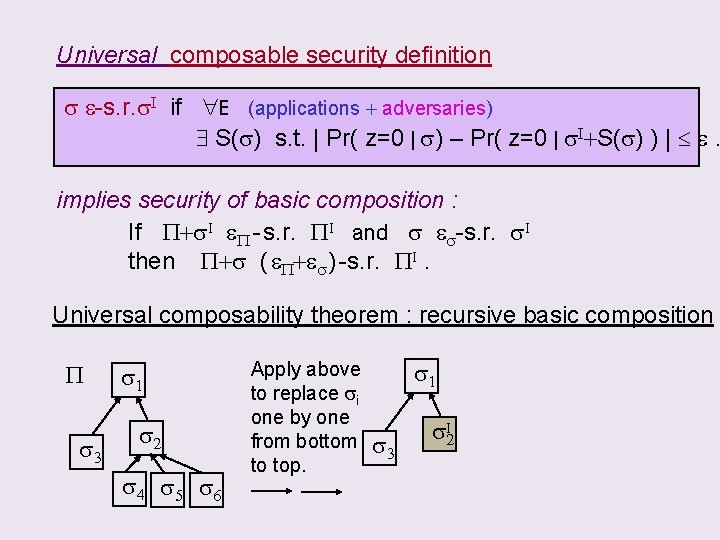
Universal composable security definition s e-s. r. s. I if E (applications + adversaries) S(s) s. t. | Pr( z=0 | s) – Pr( z=0 | s. I+S(s) ) | e. implies security of basic composition : If P+s. I e. P - s. r. PI and s es-s. r. s. I then P+s ( e. P+es ) -s. r. PI. Universal composability theorem : recursive basic composition P s 3 s 1 s 2 s 4 s 5 s 6 Apply above to replace si one by one from bottom to top. s 1 s 3 s. I 2

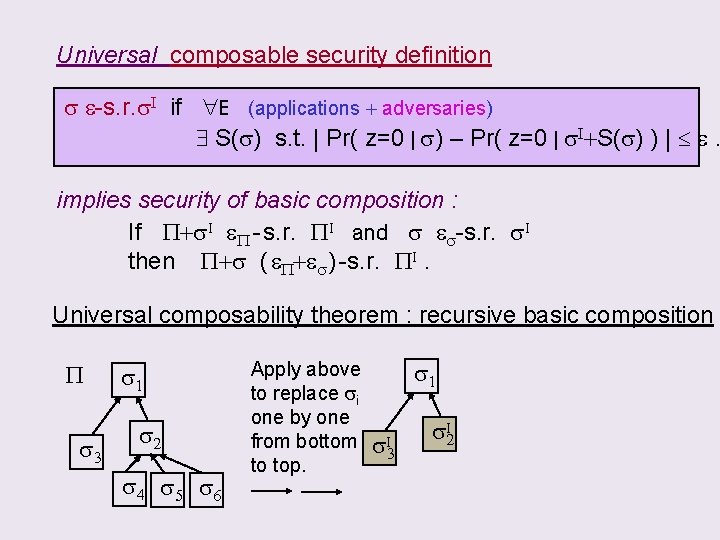
Universal composable security definition s e-s. r. s. I if E (applications + adversaries) S(s) s. t. | Pr( z=0 | s) – Pr( z=0 | s. I+S(s) ) | e. implies security of basic composition : If P+s. I e. P - s. r. PI and s es-s. r. s. I then P+s ( e. P+es ) -s. r. PI. Universal composability theorem : recursive basic composition P s 3 s 1 s 2 s 4 s 5 s 6 Apply above to replace si one by one from bottom to top. s 1 s 3 I s. I 2

Universal composable security definition s e-s. r. s. I if E (applications + adversaries) S(s) s. t. | Pr( z=0 | s) – Pr( z=0 | s. I+S(s) ) | e. implies security of basic composition : If P+s. I e. P - s. r. PI and s es-s. r. s. I then P+s ( e. P+es ) -s. r. PI. Universal composability theorem : recursive basic composition P s 3 s 1 s 2 s 4 s 5 s 6 Apply above to replace si one by one from bottom to top. s. I 1

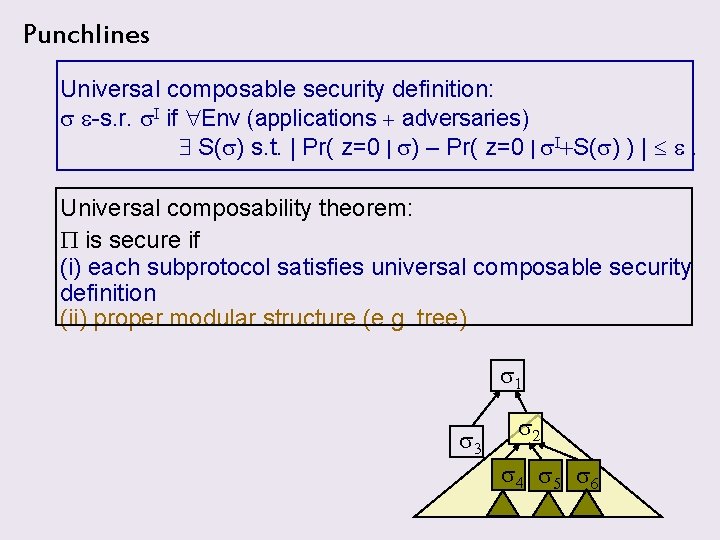
Punchlines Universal composable security definition: s e-s. r. s. I if Env (applications + adversaries) S(s) s. t. | Pr( z=0 | s) – Pr( z=0 | s. I+S(s) ) | e. Universal composability theorem: P is secure if (i) each subprotocol satisfies universal composable security definition (ii) proper modular structure (e. g. tree) s 1 s 3 s 2 s 4 s 5 s 6

Application 1 : composability of QKD 1. Composable security definition for QKD 2. Relation between composable & usual security definition 3. Sufficient conditions for composable security defintion for QKD 2 & 3 QKD is composable 4. Corollary: slow key degradation in repeated QKD Michael Ben-Or, Michal Horedecki, L, Dominic Mayers, Jonathan Oppenheim 02 Renner & Konig 04 : alternative proof for composability of QKD showing composability of quantum privacy amplication Also : Christandl, Renner, & Ekert 04 In the talk: privacy & uniformity condition only, omit equality cond (See paper for full treatment. )

Application 1: Composability of QKD (security Auth: a Ideal auth: a. I k I)Ideal KD : k. I of. QKD: k+a QKD k+a. I E k, m QKD Eve z rk QKD: k+a where a = composable authentication (e. g. Wegman-Carter 81) k+a s. r k+a. I if a is composable (thus consider the latter) Input : none Output : key k, key length m (random variable, m=0 means “fail” or “abort”) Best application for E : just accept k

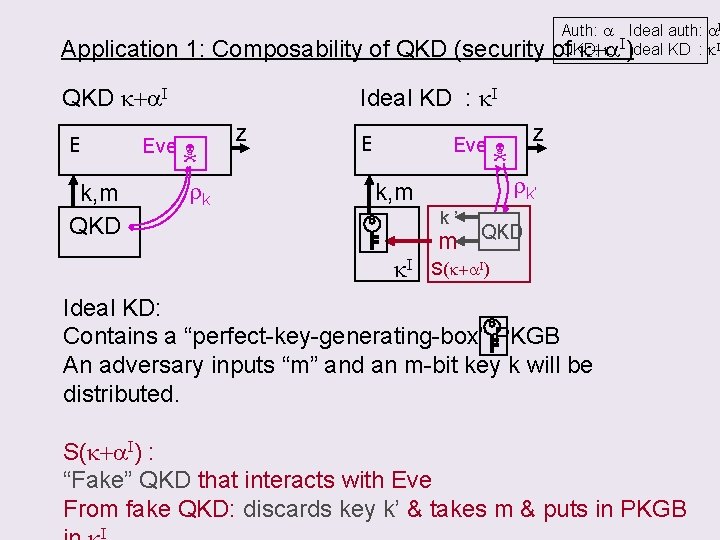
Application 1: Composability of QKD (security QKD k+a. I E Ideal KD : k. I Eve k, m QKD Auth: a Ideal auth: a. I k I)Ideal KD : k. I of. QKD: k+a rk z Eve rk’ k, m k’ k. I m QKD S(k+a. I) Ideal KD: Contains a “perfect-key-generating-box” PKGB An adversary inputs “m” and an m-bit key k will be distributed. S(k+a. I) : “Fake” QKD that interacts with Eve From fake QKD: discards key k’ & takes m & puts in PKGB I

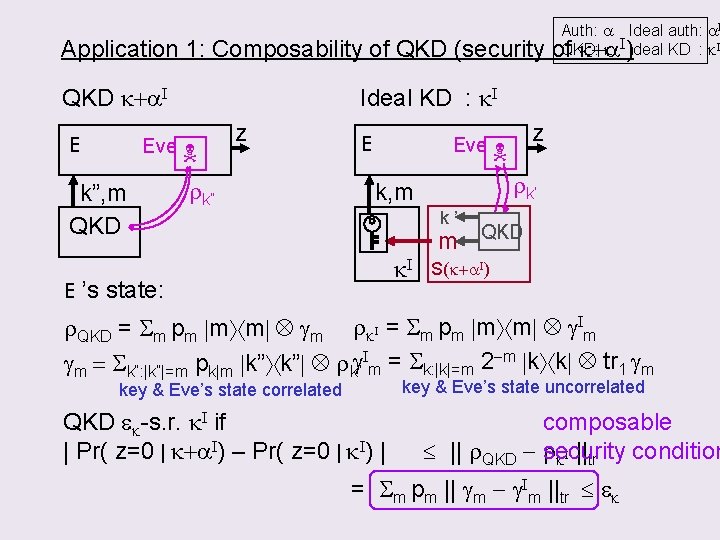
Application 1: Composability of QKD (security QKD k+a. I E Ideal KD : k. I Eve k”, m QKD Auth: a Ideal auth: a. I k I)Ideal KD : k. I of. QKD: k+a z rk” E z Eve rk’ k, m k’ k. I E ’s state: m QKD S(k+a. I) r. QKD = Sm pm m m gm rk. I = Sm pm m m g. Im gm = Sk”: |k”|=m pk|m k” k” rk”g. Im = Sk: |k|=m 2 -m k k tr 1 gm key & Eve’s state uncorrelated key & Eve’s state correlated QKD ek-s. r. k. I if | Pr( z=0 | k+a. I) – Pr( z=0 | k. I) | composable || r. QKD - security rk. I ||tr condition = Sm pm || gm - g. Im ||tr ek

Application 1: Composability of QKD (security Auth: a Ideal auth: a. I k I)Ideal KD : k. I of. QKD: k+a gm = Sk: |k|=m pk|m k k rk g. Im = Sk: |k|=m 2 -m k k tr 1 gm QKD ek-s. r. k. I if Security : correlation Sm pm || gm - g. Im ||tr indistinguishable ek from none (assuming uniformity : pk|m 2 security: Sufficient conditions for composable 1. Usual security If Sm pm I(KE: K | M=m) m , then, ek (2 max(m)+2 m)1/2 2. Small Holevo info of Eve Let Em = {pk|m , rk}k: |k|=m If Sm pm c(Em) m , then, ek (2 ln 2 m)1/2 3. High singlet fidelity (if proof by EPP) Let hm be state of Alice & Bob , F m m-singlet state equality + If Sm pm F(hm , F m) 1 -m , then, ek m 1/2 uniformity

Punchlines QKD does provide a key that can be safely used in quantum / classical applications designed to use a perfect key !!! Bounds for Eve’s Holevo info or singlet fidelity may be tighter in the context of composability, compared to those for mutual info Proofs for sufficient conditions are relations between corelation measures

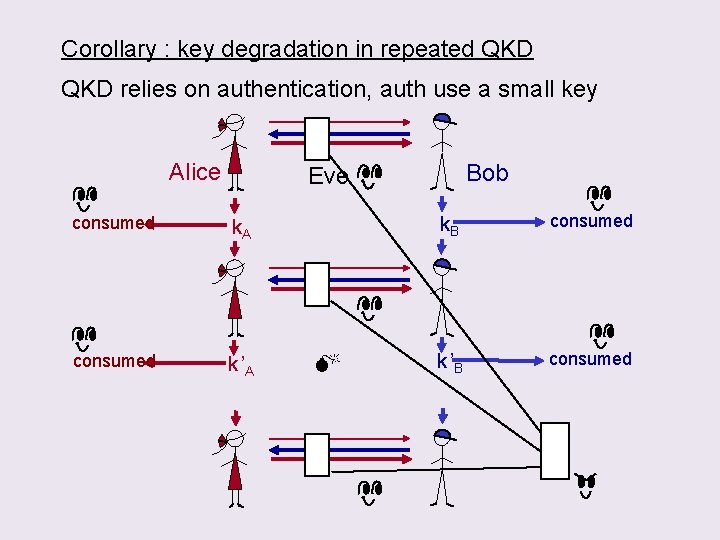
Corollary : key degradation in repeated QKD relies on authentication, auth use a small key Alice Bob Eve consumed k. A consumed k ’A k. B consumed k ’B consumed

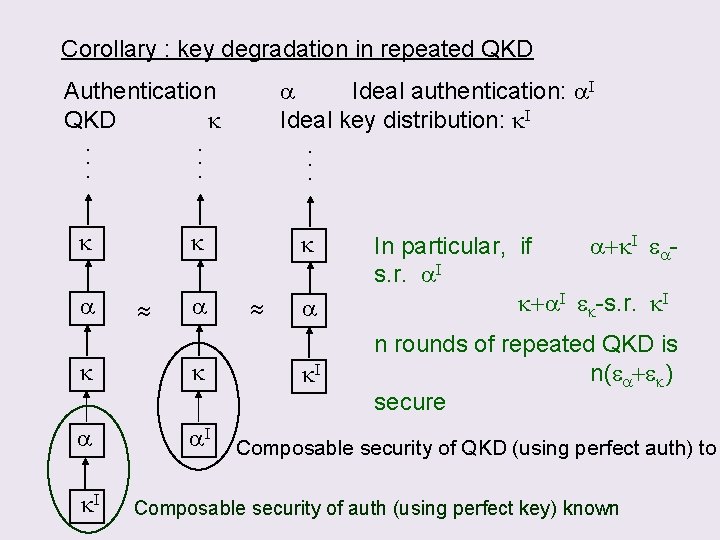
Corollary : key degradation in repeated QKD a Ideal authentication: a. I Ideal key distribution: k. I . . Authentication QKD k k a a. I k. I a k. I In particular, if a+k. I eas. r. a. I k+a. I ek-s. r. k. I n rounds of repeated QKD is n(ea+ek) secure Composable security of QKD (using perfect auth) to Composable security of auth (using perfect key) known

Composability of “Quantum Auth + key recycling” Patrick Hayden, L, Dominic Mayers 04 Oppenheim & Horodecki 03 : proof for secure key recycling via bounds on information theoretic quantities

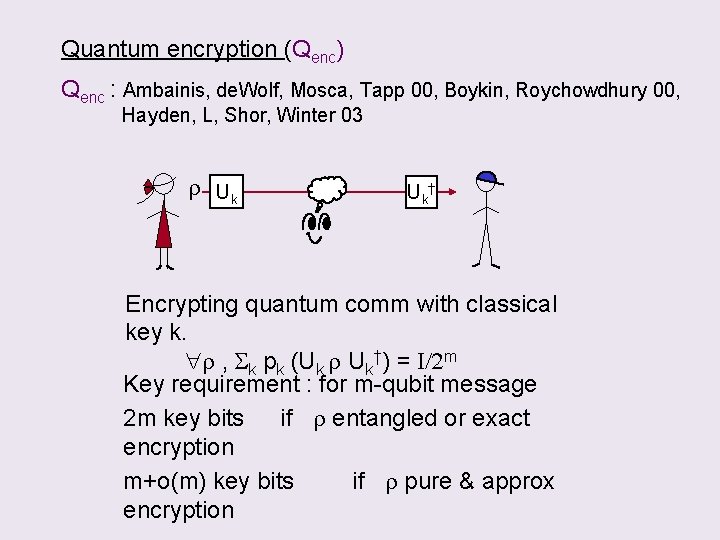
Quantum encryption (Qenc) Qenc : Ambainis, de. Wolf, Mosca, Tapp 00, Boykin, Roychowdhury 00, Hayden, L, Shor, Winter 03 r Uk Uk † Encrypting quantum comm with classical key k. r , Sk pk (Uk r Uk†) = I/2 m Key requirement : for m-qubit message 2 m key bits if r entangled or exact encryption m+o(m) key bits if r pure & approx encryption

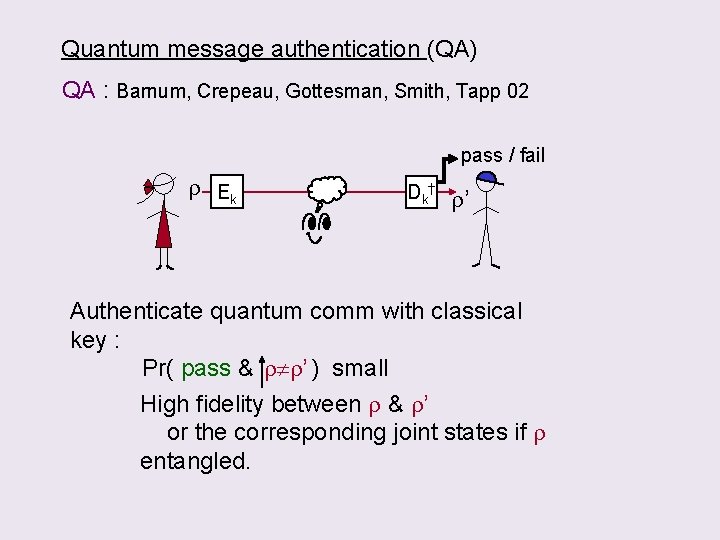
Quantum message authentication (QA) QA : Barnum, Crepeau, Gottesman, Smith, Tapp 02 pass / fail r Ek Dk † r’ Authenticate quantum comm with classical key : Pr( pass & r r’ ) small High fidelity between r & r’ or the corresponding joint states if r entangled.

Eavesdropping a quantum state disturbs it. 2 interpretations of key recycling in 2. Add QA to Qenc , passing the auth test suggests QAno eavesdropping 1. QA always requires Qenc (BCGST 02) Can we eliminate this cost? Can we recycle the key ? Prob(authentication passes and eavesdropped) negligible. Key recycling : intuitive (BBBW 82) & obvious ? Hard to analyze joint attacks over different uses of the key. Result : QA +“key reuse if auth test passes (w/o privacy amplification)” is secure specific scheme in BCGST 02 Main ideas: 1. Redefine BCGST 02 as BCGST 02+KD 2. Show BCGST 02+KD composable (exploiting special structures of B

Composability of “BCGST 02+KD” 1. Review BCGST 02 2. “Equate” BCGST 02 & TQA (auth by teleportation) 3. Prove composability of TQA+KD = composability of “ebits” For same token: 1. BCGST 02’ for pure states using approx encryption for half the price. 2. Quantum composability of Wegman-Carter scheme

Scenario for BCGST 02 Alice & Bob has : 1. Classical key 2. Insecure quantum channel 3. Forward classical channel (Alice → Bob) (WLOG authenticated) 4. No back comm (non interactive, e. g. quantum storage) We use 1 bit of back comm for key recycling – to tell Alice if auth passes. Still applies to quantum storage & not too interactive.

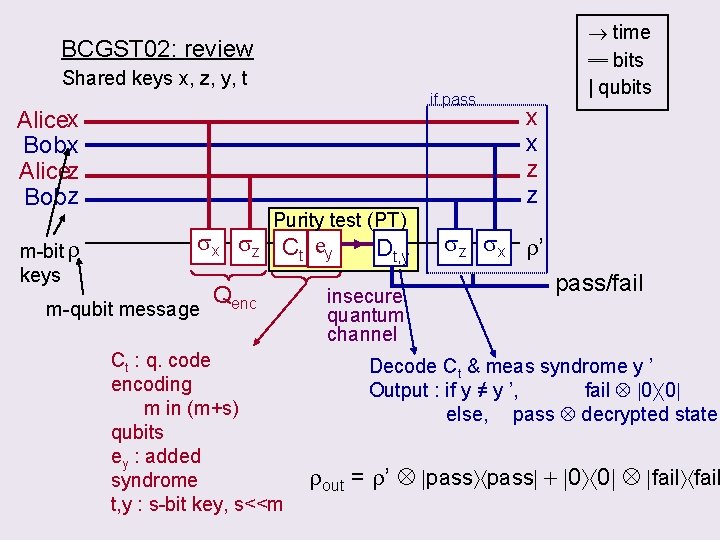
time ═ bits | qubits BCGST 02: review Shared keys x, z, y, t if pass Alicex Bob x Alicez Bobz m-bit r keys Purity test (PT) sx sz C t e y m-qubit message Qenc Ct : q. code encoding m in (m+s) qubits ey : added syndrome t, y : s-bit key, s<<m Dt, y insecure quantum channel x x z z sz sx r’ pass/fail Decode Ct & meas syndrome y ’ Output : if y ≠ y ’, fail 0 0 else, pass decrypted state rout = r’ pass + 0 0 fail

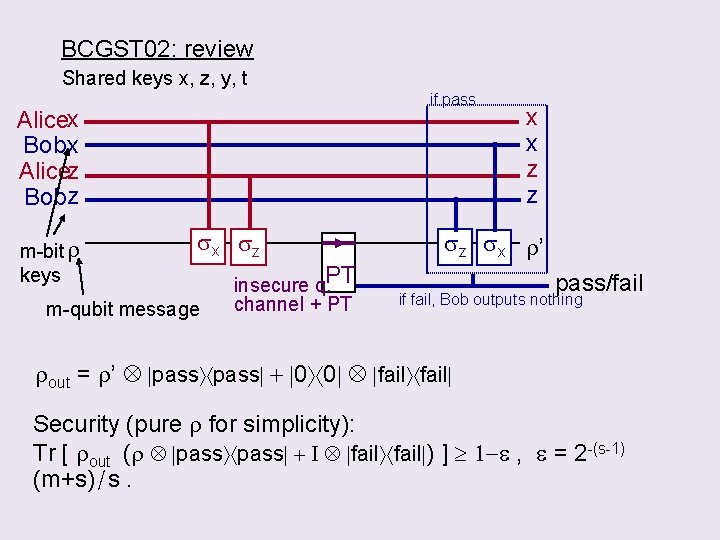
BCGST 02: review Shared keys x, z, y, t if pass Alicex Bob x Alicez Bobz m-bit r keys sx sz m-qubit message insecure q. PT channel + PT x x z z sz sx r’ pass/fail if fail, Bob outputs nothing rout = r’ pass + 0 0 fail Security (pure r for simplicity): Tr [ rout (r pass + I fail ) ] 1 -e , e = 2 -(s-1) (m+s)/s.

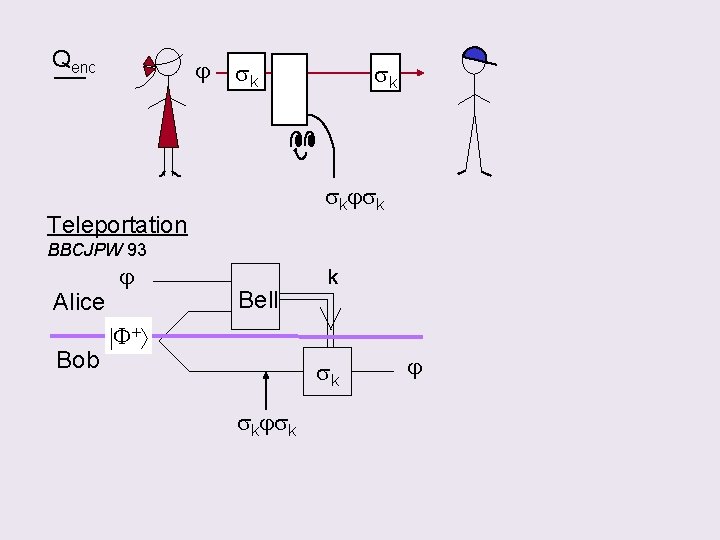
Qenc j sk sk skjsk Teleportation BBCJPW 93 Alice Bob j Bell k F+ sk skjsk j

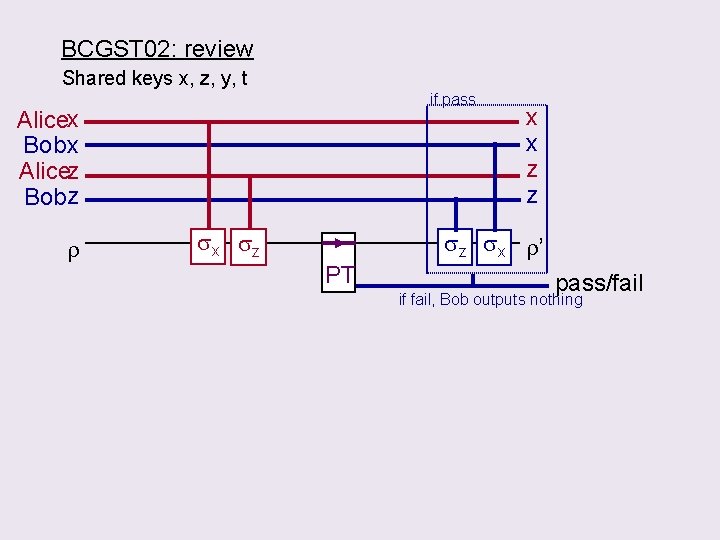
BCGST 02: review Shared keys x, z, y, t if pass Alicex Bob x Alicez Bobz r sx sz x x z z sz sx r’ PT pass/fail if fail, Bob outputs nothing

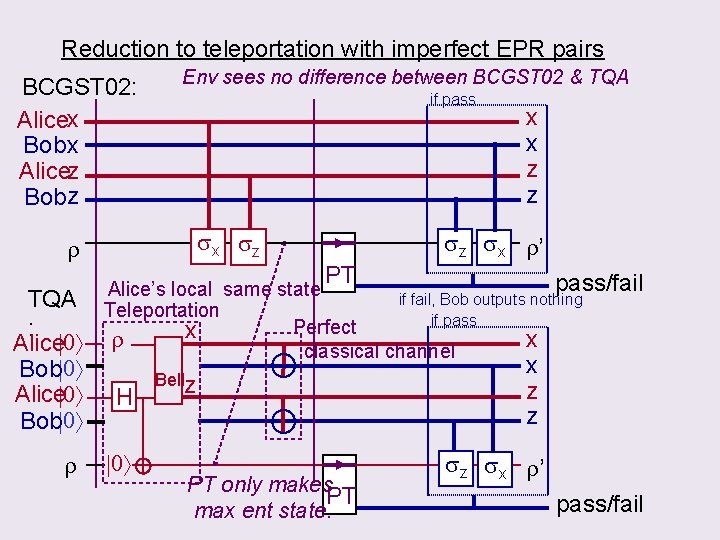
Reduction to teleportation with imperfect EPR pairs BCGST 02: Alicex Bob x Alicez Bobz Env sees no difference between BCGST 02 & TQA if pass sx sz r TQA : Alice 0 Bob 0 r x x z z sz sx r’ PT pass/fail Alice’s local same state if fail, Bob outputs nothing Teleportation if pass Perfect x x r classical channel H 0 Bellz PT only makes PT max ent state. x z z sz sx r’ pass/fail

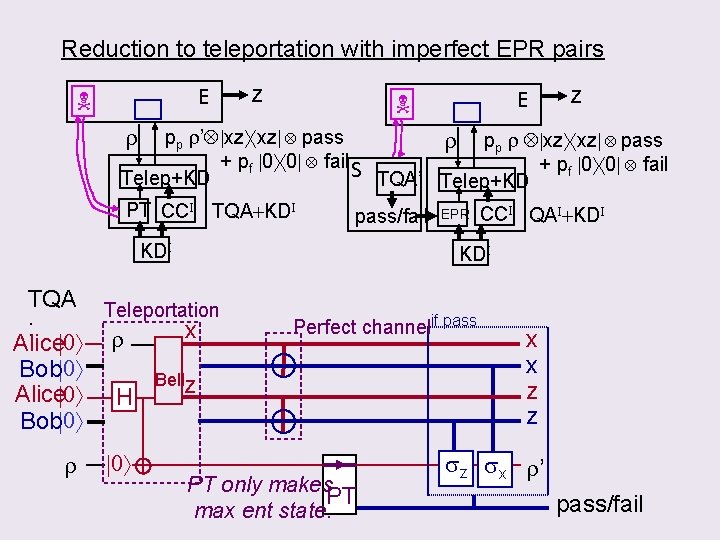
Reduction to teleportation with imperfect EPR pairs E z r pp r’ xz xz pass r pp r xz xz pass + pf 0 0 fail S + pf 0 0 fail Telep+KD TQA’ Telep+KD PT CCI TQA+KDI pass/fail EPR CCI QAI+KDI KDI TQA Teleportation : x Alice 0 r Bob 0 Bellz Alice 0 H Bob 0 r 0 Perfect channelif pass PT only makes PT max ent state. x x z z sz sx r’ pass/fail

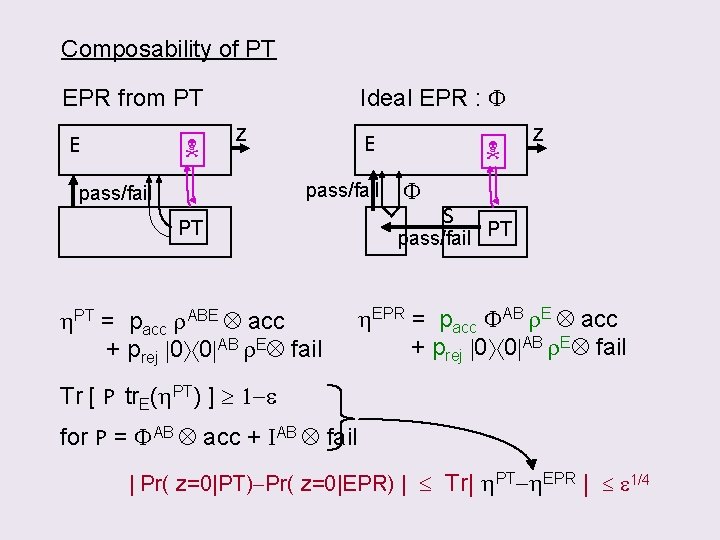
Composability of PT Ideal EPR : F EPR from PT E z E pass/fail PT h. PT = pacc r. ABE acc + prej 0 0 AB r. E fail F z S pass/fail PT h. EPR = pacc FAB r. E acc + prej 0 0 AB r. E fail Tr [ P tr. E(h. PT) ] 1 -e for P = FAB acc + IAB fail | Pr( z=0|PT)-Pr( z=0|EPR) | Tr| h. PT-h. EPR | e 1/4

Bonus materials: Lower bounds for QA & pure state authentication Qenc : r , Sk pk (Uk r Uk†) = I/2 m key size 2 m bits (Ambainis, de. Wolf, Mosca, Tapp 00 Boykin, Roychowdhury 00) Approx Pure state APQenc : j || (1/n) Σk Uk j j Uk† - I/2 m ||tr ≤ ε key size m + o(m) bits (Hayden, L, Shor, Winter 03) APQenc Remote state preparation ┊ ┊ Qenc Teleportation Can we replace Qenc in BCGST 02 by APQenc securely?

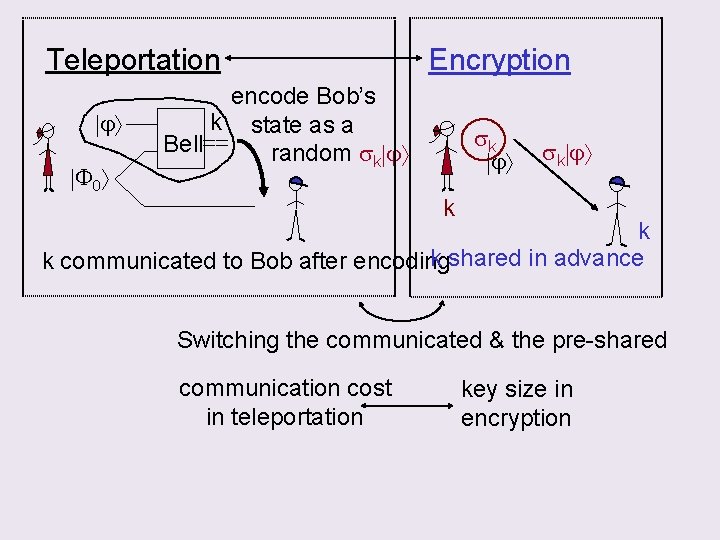
Teleportation j F 0 Encryption encode Bob’s k state as a Bell== random sk j k k k shared in advance k communicated to Bob after encoding Switching the communicated & the pre-shared communication cost in teleportation key size in encryption

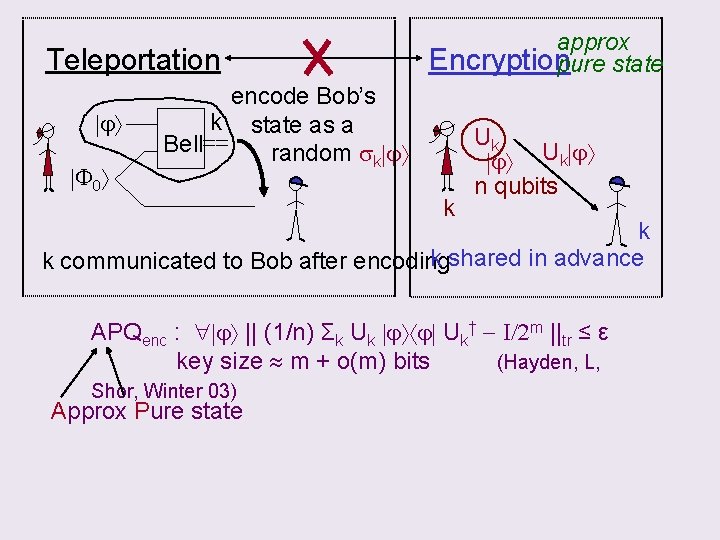
Teleportation j F 0 approx Encryptionpure state encode Bob’s k state as a Bell== random sk j k Uk j n qubits k k shared in advance k communicated to Bob after encoding APQenc : j || (1/n) Σk Uk j j Uk† - I/2 m ||tr ≤ ε key size m + o(m) bits (Hayden, L, Shor, Winter 03) Approx Pure state

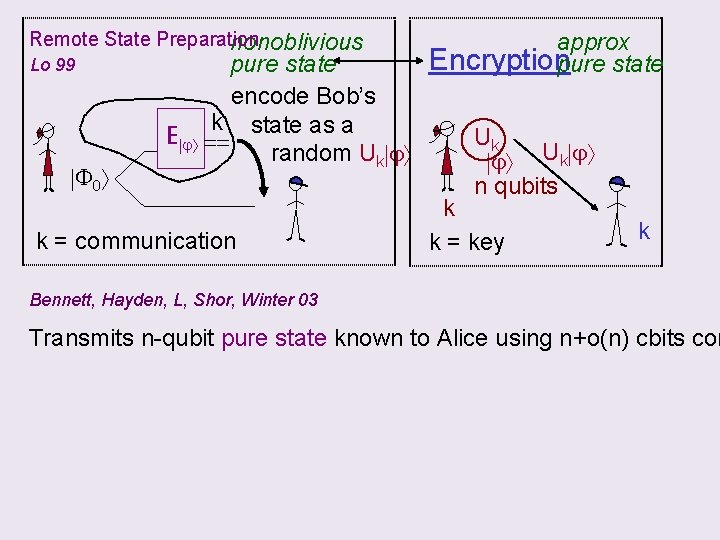
Remote State Preparation nonoblivious Lo 99 E j F 0 pure state encode Bob’s k state as a == random Uk j k = communication approx Encryptionpure state Uk j n qubits k k = key k Bennett, Hayden, L, Shor, Winter 03 Transmits n-qubit pure state known to Alice using n+o(n) cbits com

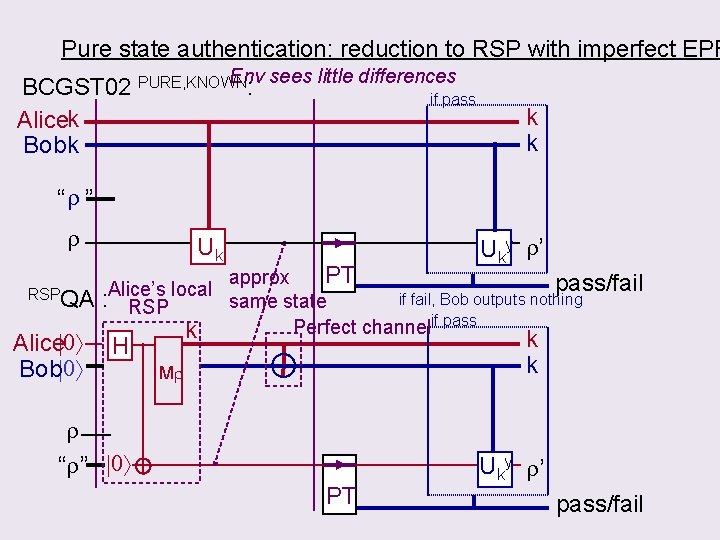
Pure state authentication: reduction to RSP with imperfect EPR Env sees little differences BCGST 02 PURE, KNOWN: Alicek Bob k if pass k k “r ” r RSPQA Alice 0 Bob 0 Uky r’ Uk PT approx pass/fail Alice’s local if fail, Bob outputs nothing : RSP same state Perfect channelif pass k k k H Mr r “r” 0 PT Uky r’ pass/fail

Conclusion Composability – gives a prescription for organizing our security into components, each simple and well-defined. To achieve composable security, we find out what will make th work – it is a systematic method to select secure variations. QKD & BCGST 02 work better than we thought. How do the difficulties disappear?