Application of Network Flows Matrix Rounding CSE IIT
![Feasible Flow Problem Formulation x 1 [18, 19] s [9, 10] [6, 7] [4,](https://slidetodoc.com/presentation_image_h/841f604a8fab48f4af2383fedff61741/image-5.jpg "Feasible Flow Problem Formulation x 1 [18, 19] s [9, 10] [6, 7] [4,")
![Feasible Circulation Problem Add an edge from t → s with bounds [0, ∞]](https://slidetodoc.com/presentation_image_h/841f604a8fab48f4af2383fedff61741/image-7.jpg "Feasible Circulation Problem Add an edge from t → s with bounds [0, ∞]")
![Transportation Problem c(x 1, y 1) = 1 x 1 [18, 19] l-(v) =](https://slidetodoc.com/presentation_image_h/841f604a8fab48f4af2383fedff61741/image-9.jpg "Transportation Problem c(x 1, y 1) = 1 x 1 [18, 19] l-(v) =")
- Slides: 11
Application of Network Flows: Matrix Rounding CSE, IIT KGP
Matrix Rounding • y 1 y 2 y 3 x 1 x 2 x 3 Ʃ CSE, IIT KGP [16, 17] 10. 9 16. 5 [14, 15] 14. 4 [10, 11] Ʃ [18, 19] 18. 5 [9, 10] 9. 8 [13, 14] 13. 5
Solution • Step 1: Represent the consistent rounding problem as a feasible flow problem. • Step 2: Convert the feasible flow problem into a feasible circulation problem. • Step 3: Convert the feasible circulation problem into a transportation problem. • Step 4: Convert the transportation problem into a network flows problem. CSE, IIT KGP
Solution • Step 1: Represent the consistent rounding problem as a feasible flow problem. • Step 2: Convert the feasible flow problem into a feasible circulation problem. • Step 3: Convert the feasible circulation problem into a transportation problem. • Step 4: Convert the transportation problem into a network flows problem. CSE, IIT KGP
Feasible Flow Problem Formulation x 1 [18, 19] s [9, 10] [6, 7] [4, 5] x 2 [4, 5] y 1 [7, 8] [5, 6] y 2 [2, 3] [16, 17] [14, 15] [2, 3] [13, 14] y 1 x 3 y 2 [4, 5] y y 3 [3, 4] 3 [18, 19] x 2 [9, 10] x 3 [13, 14] CSE, IIT KGP [16, 17] [14, 15] [10, 11] t
Solution • Step 1: Represent the consistent rounding problem as a feasible flow problem. • Step 2: Convert the feasible flow problem into a feasible circulation problem. • Step 3: Convert the feasible circulation problem into a transportation problem. • Step 4: Convert the transportation problem into a network flows problem. CSE, IIT KGP
Feasible Circulation Problem Add an edge from t → s with bounds [0, ∞] x 1 [18, 19] s [9, 10] [6, 7] [4, 5] x 2 [4, 5] [13, 14] [7, 8] [5, 6] [2, 3] y 2 [2, 3] x 3 [16, 17] [14, 15] [10, 11] [4, 5] [3, 4] [0, ∞] CSE, IIT KGP y 1 y 3 t
Solution • Step 1: Represent the consistent rounding problem as a feasible flow problem. • Step 2: Convert the feasible flow problem into a feasible circulation problem. • Step 3: Convert the feasible circulation problem into a transportation problem. • Step 4: Convert the transportation problem into a network flows problem. CSE, IIT KGP
Transportation Problem c(x 1, y 1) = 1 x 1 [18, 19] l-(v) = 18 l+(v) = 6+7+4=17 b(v) = 18 -17 = 1 s [9, 10] [6, 7] [4, 5] x 2 [4, 5] [13, 14] [7, 8] [5, 6] [2, 3] y 2 [2, 3] x 3 [16, 17] [14, 15] [10, 11] [4, 5] [3, 4] CSE, IIT KGP y 1 [0, ∞] y 3 t
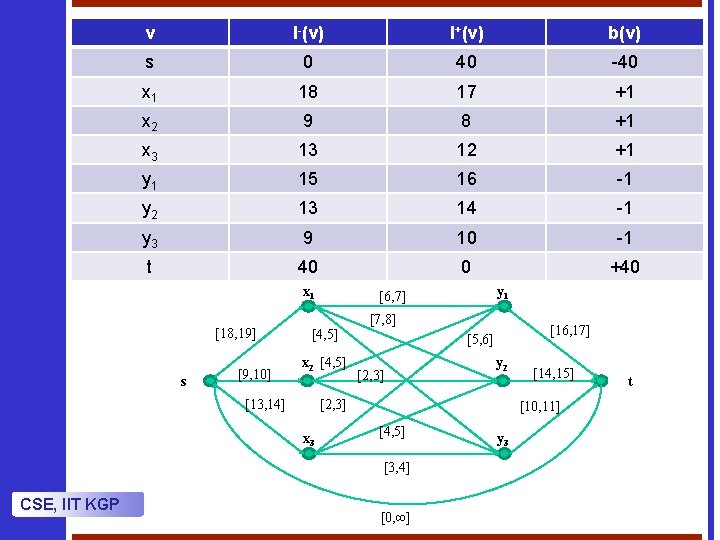
v l-(v) l+(v) b(v) s 0 40 -40 x 1 18 17 +1 x 2 9 8 +1 x 3 13 12 +1 y 1 15 16 -1 y 2 13 14 -1 y 3 9 10 -1 t 40 0 +40 x 1 [18, 19] s [9, 10] [4, 5] x 2 [4, 5] [13, 14] [7, 8] [16, 17] [5, 6] [2, 3] y 2 [2, 3] x 3 [14, 15] [10, 11] [4, 5] [3, 4] CSE, IIT KGP y 1 [6, 7] [0, ∞] y 3 t
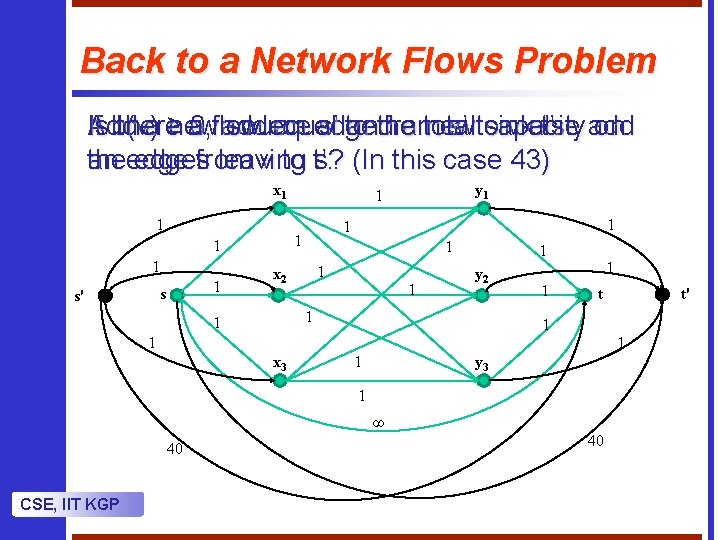
Back to a Network Flows Problem Add a new source s’ and a new sink t’. If b(v) ≥ 0, add an edge from s’ to v else add Is there a flow equal to the total capacity on an edge from v to t’. the edges leaving s? (In this case 43) x 1 1 s s' 1 1 y 1 1 x 2 1 1 y 2 1 1 t 1 1 1 x 3 1 y 3 1 ∞ 40 CSE, IIT KGP t' 40