Application of linked list Geletaw S Linked list

Application of linked list Geletaw S.

Linked list can be used in various environment. Some of the common examples are l Creation of a polynomial l Polynomial manipulation l Sorting l Creation of a tree l Tree Traversals l Multilist Organization

Creation of a Polynomial l. A node is used to create a list which consist of various components of the polynomial l Example of a polynomial 4 x^3 + 3 x^2 + 2 x + 1 Node 2 Node 3 Node 4

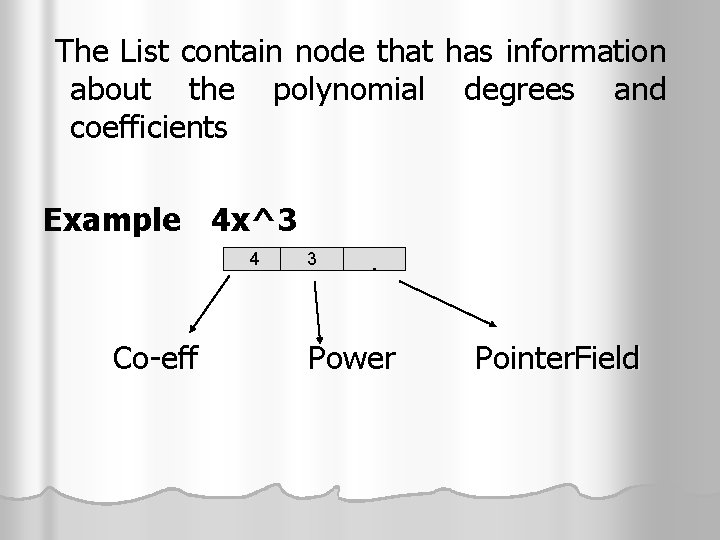
The List contain node that has information about the polynomial degrees and coefficients Example 4 x^3 4 Co-eff 3 . Power Pointer. Field

Similarly for the polynomial 4 x^3 + 3 x^2 + 2 x + 1, the linked list created is as follows 4 3 3 2 2 1 1 Structure used to create a node: Struct node { int power; int coeff; struct node * next; } // to point the next node in the list 0

Procedure to create a polynomial Void create( ) { int s, c 1; Struct node * p 1, *n; root = p 1 = NULL; cout<<“ enter the higher degree”; cin>>deg; s = sizeof ( struct node *); for (I = deg; i>+0; I - - ) { cout<<“co-efficient : ”; cin>> c 1; n=(struct node *) new(s); n -> coeff = c 1; n -> pow = I; n -> next = NULL; if (root = = NULL) root = n; else p 1 -> next = n; p 1=n; }

Algorithm to create a polynomial l The highest degree of the polynomial is obtained first l Based on the degree the node is created l The co-efficient and the corresponding power value is stored in the node l The NEXT pointer is updated accordingly

Type declaration for array implementation of the polynomial ADT Typedef struct { int coeffarray[ Maxdegree + 1 ]; int Highpower; } *Polynomial; Procedure to initialize a polynomial to zero Void zero. Polynomial( Polynomial Poly ) { int i; for( i=0; i<=Maxdegree; i++ ) Poly -> Coeff. Array[ i ] = o Poly -> High. Power = o; }

Procedure to add two Polynomials Void Add. Polynomial( const Polynomial Poly 1, const Polynomial Poly 2, Polynomail Poly. Sum) { int i; zero. Polynomial( Poly. Sum ); Polysum -> High. Power = Max( Poly 1 -> High. Power, Poly 2 -> Highpower); for( i= Poly. Sum -> High. Power; i>=0; i++) Poly. Sum ->Coeff. Array[ i ] = Poly 1 -> coeff. Array [ i ] + Poly 2 ->coeff. Array[ i ]; }

Poly. Sum Poly 1 Poly 2 4 x^3 + 3 x^2 + 2 x + 1 5 x^2 + 6 x + 3 (+) -----------------Poly. Sum 4 x^3 + 8 X^2 + 8 x + 4

Procedure to Multiply 2 Polynomials Void Mult. Polynomial( const Polynomial Poly 1, const Polynomial Poly 2, Polynomial Poly. Prod) { int i, j; zero. Polynomial( Poly. Prod ); Poly. Prod -> High. Power = Poly 1 -> high. Power + Poly 2 ->High. Power; if( Poly. Prod -> High. Power > Max. Degree) error( “ Exceeded array Size”); else for( i=0; i<= Poly 1 -> high. Power; i++) for( j=0; j<= Poly 2 -> High. Power; J++) Poly. Prod -> coeff. Array [ i+j ] = Poly 1 -> coeff. Array [i] * Poly 2 -> coeff. Array [j]; }

Poly. Prod Poly 1 Poly 2 4 x^3 + 3 x^2 + 2 x + 1 5 x^2 + 6 x + 3 (*) -----------------20 x^5 + 24 x^4 + 12 x^3 + 15 x^4 + 18 x^3 + 6 x^2 + 10 x^3 + 12 x^2 + 6 x + 5 x^2 + 6 x + 3 Poly. Prod 20 x^5 + 39 x^4 + 40 x^3 + 23 x^2 + 12 x + 3

Radix Sort l It is performed using buckets from 0 to 9 l The digit position of a number is used to perform sorting l The number of passes in a radix sort depends on the number of digits in the given number l It is also called as Card Sort

Example 42, 24, 11, 36, 54, 10, 19, 27, 45. The number of digits n the numbers are 2, hence the number of passes are 2 Pass 1 32 54 24 45 36 27 4 5 6 7 10 11 42 0 1 2 3 19 8 9

The number has been placed in their corresponding pockets based on their unit digit. 10 is placed in pocket 0 27 is placed in pocket 7 Collect back all the nos from the pockets 10, 11, 42, 32, 24, 54, 45, 36, 27, 19

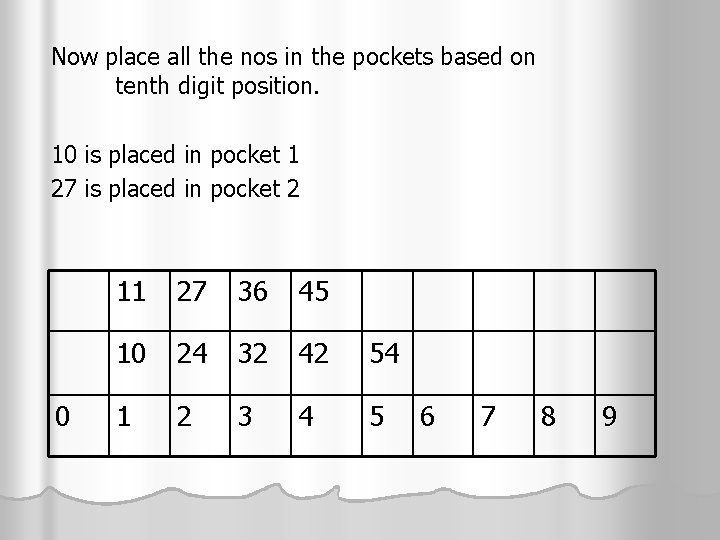
Now place all the nos in the pockets based on tenth digit position. 10 is placed in pocket 1 27 is placed in pocket 2 0 11 27 36 45 10 24 32 42 54 1 2 3 4 5 6 7 8 9