Application of Data Compression to the MILSTD1553 Data

Application of Data Compression to the MIL-STD-1553 Data Bus Scholar’s Day Feb. 1, 2008 By Bernard Lam

Overview n Background n MIL-STD-1553 Bus Trace Analysis n Solutions – Compression Algorithms n n Zero-Tracking, Modified Run-Length, and Differential Error Analysis n Conclusions & Future Research n

Goal Of Research n To extend the bandwidth capabilities of MILSTD-1553 Bus, using compression techniques. n Develop algorithms suitable for legacy systems n Demonstrate that the time to compress and decompress data is offset by the overall savings in data transmission time.

Timing Analysis Timing Diagram

Background ~ MIL-STD-1553 n MIL-STD-1553 serial data bus Developed in the late 1960’s and early 1970’s n Limited/Low Bandwidth n n 1 Mb/s n Has lead to development of multiple independent busses n Time division multiple (TDM) access System Model

Background ~ MIL-STD-1553 n MIL-STD-1553 (cont’d) Manchester Bi-phase encoding n Data word size: 16 bit Message Format n Sync Waveform n Parity Bit n

Background ~ MIL-STD-1553 n MIL-STD-1553 (cont’d) Max. single-command transmission size of 32 words n Safety and Mission Critical System n Real-Time System n n Replacement of MIL-STD-1553 with updated bus protocol, such as Fibre Channel, not a viable solution because of extensive costs.

Bus Trace Analysis n Analysis was conducted using data from multiple bus traces of data captured at the F/A – 18 Advanced Weapons Laboratory. n Each trace represented roughly 30 seconds of flight data and included examples of mode changes and start-up conditions.

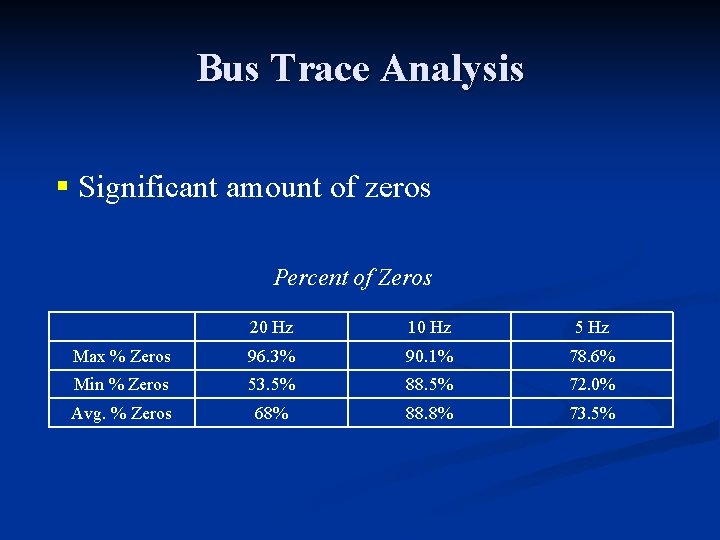
Bus Trace Analysis § Significant amount of zeros Percent of Zeros 20 Hz 10 Hz 5 Hz Max % Zeros 96. 3% 90. 1% 78. 6% Min % Zeros 53. 5% 88. 5% 72. 0% Avg. % Zeros 68% 88. 8% 73. 5%

Bus Trace Analysis § Limited number of changes between consecutive message transmissions Percent of Changes 20 Hz 10 Hz 5 Hz Max % Changes 21. 7% 27. 5% 78. 6% Min % Changes 2. 0% 0% 2% Avg. % Changes 3. 9% 3. 3%

Data Compression n Lossless vs. Lossy Compression n Lossless n Original data is completely retrievable by means of decompression n Ex. Winzip, GIF n Lossy n Lose information; original data not retrievable when decompressed n Higher Compression Ratios n E. g. , jpeg, mp 3

Data Compression n Coding Performance and Efficiency n Measured by compression ratio FFFF AFC 1 FFFF xxxx FFFF compress yyyy decompress AFC 1

Data Compression n Criteria n Lossless Compression n Take advantage of message format of MIL-STD 1553 n Limit worst case expansion n Limit computational and memory requirements

Compression Algorithms n Common Value Tracking n Zero-Tracking n Modified Run-Length Encoding n Differential Encoding

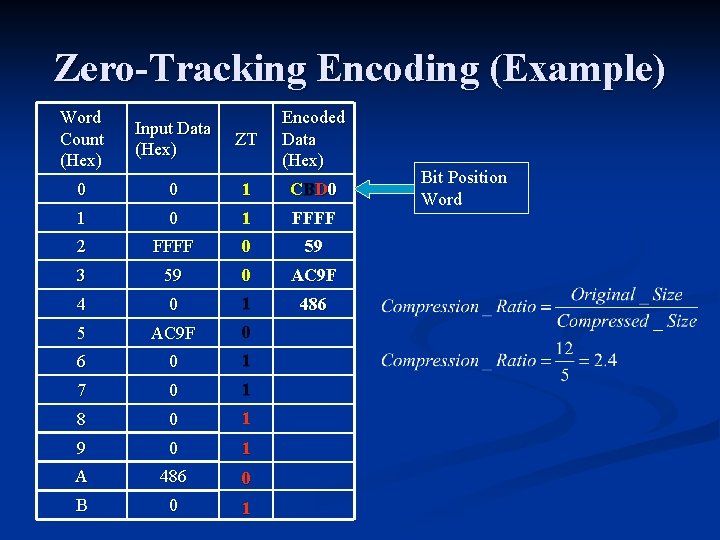
Zero Tracking n Encodes long sequences containing mostly zeros Uses marker sequence to indicate the position of zeros n Transmits n Position Address (marker sequence) n Non-Zero Data Words n

Zero-Tracking Encoding (Example) Word Count (Hex) Input Data (Hex) ZT Encoded Data (Hex) 0 0 1 CB D 0 1 FFFF 2 FFFF 0 59 3 59 0 AC 9 F 4 0 1 486 5 AC 9 F 0 6 0 1 7 0 1 8 0 1 9 0 1 A 486 0 B 0 1 Bit Position Word

Zero Tracking n If a 32 -word block is compressed 2 data words are required to indicate positions n Can transmit maximum of 31 uncompressed data words n n Most significant bit in 1 st address word is used to indicate if uncompress/compressed n Worst Case Compression Ratio n comp. ratio = 31/32

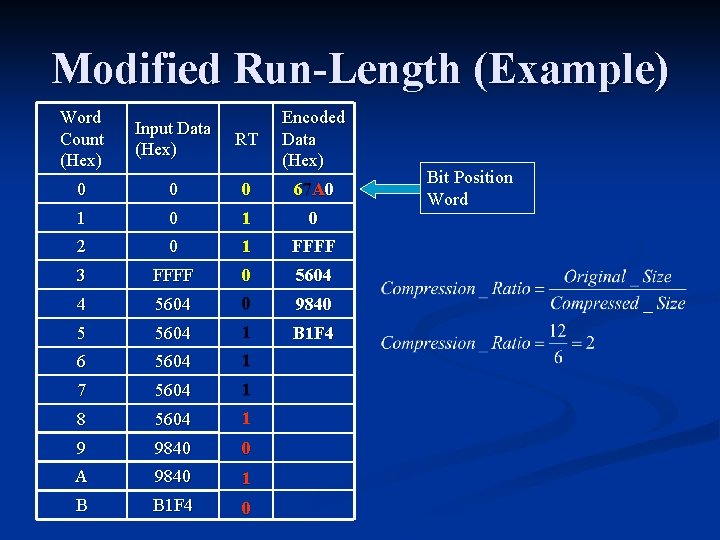
Modified Run-Length Encoding n Encodes consecutive sequences of identical words n Uses marker sequence to indicate the presence of repeated sequences within block set n For block of 32 words n Worst Case Expansion – 31/32

Modified Run-Length (Example) Word Count (Hex) Input Data (Hex) RT Encoded Data (Hex) 0 0 0 67 A 0 1 0 2 0 1 FFFF 3 FFFF 0 5604 4 5604 0 9840 5 5604 1 B 1 F 4 6 5604 1 7 5604 1 8 5604 1 9 9840 0 A 9840 1 B B 1 F 4 0 Bit Position Word

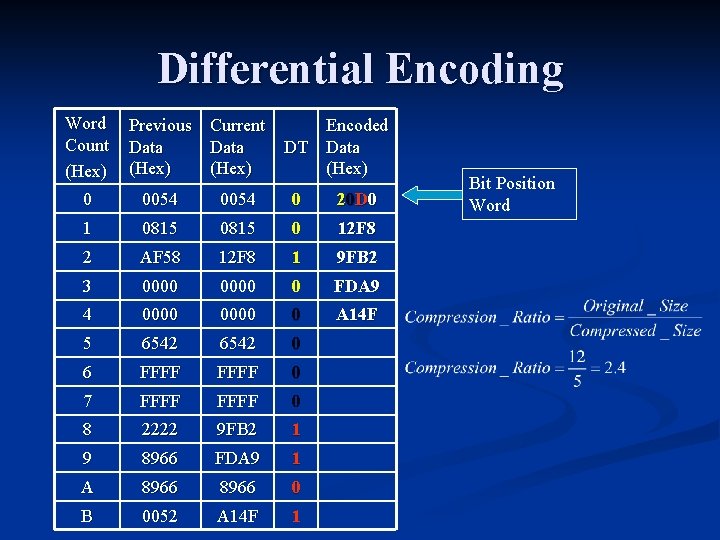
Differential Encoding Encodes only changes of previous vs. current word locations n A differential scheme takes advantage of the fact that for a given rate group one transmission to the next does not change n Two buffers are required for comparison of previous and current transmissions n

Differential Encoding Word Count (Hex) Previous Current Data (Hex) Encoded DT Data (Hex) 0 0054 0 20 D 0 1 0815 0 12 F 8 2 AF 58 12 F 8 1 9 FB 2 3 0000 0 FDA 9 4 0000 0 A 14 F 5 6542 0 6 FFFF 0 7 FFFF 0 8 2222 9 FB 2 1 9 8966 FDA 9 1 A 8966 0 B 0052 A 14 F 1 Bit Position Word

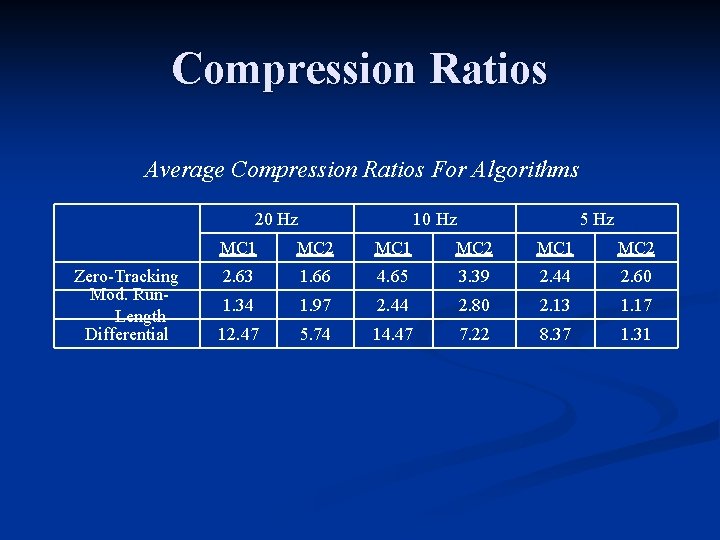
Compression Ratios Average Compression Ratios For Algorithms 20 Hz Zero-Tracking Mod. Run. Length Differential 10 Hz 5 Hz MC 1 MC 2 2. 63 1. 66 4. 65 3. 39 2. 44 2. 60 1. 34 1. 97 2. 44 2. 80 2. 13 1. 17 12. 47 5. 74 14. 47 7. 22 8. 37 1. 31

Compression Bit Status n 1 st Bit of 1 st 16 -bit word indicates the compression status n n ‘ 1’ - equals uncompressed ‘ 0’ – equals compressed Block Set Format Compressio n Status 10 15 bits 16 bits 31 30 Data Words Bit Position Word 31 – 16 bit Data 30 Words – 16 bit Data Words

Transmission Error Effects n Effects of data errors can be amplified when using data compression n If higher levels of error detection and correction (EDAC) are needed, one or more data words can be dedicated to EDAC

Transmission Error Effects n Standard 1553 Error Checking Bit Errors can be detected n Exception – multiple-bit errors without parity change cannot be detected n n Common Value Tracking If an undetected error is in the bit position word, multiple words can be corrupted. n If an undetected error is in the data word, only that word location is impacted n

Transmission Error Effects n Modified Run-Length Compression Like zero tracking a error in the bit position word can invalidate a run n Error dramatically worse result than that of zerotracking n n Differential Encoding Error in address word can result incorrect updating n Worst Case – All data words are updated n n Further Research Required

Future Research n Error Handling Routines n Effects of mode-changing and start-up n Timing analysis for Run-Length and Differential Encoding

Conclusions n Reviewed Statistical Analysis of Trace Data n Able to achieve compression ratios greater than one for all algorithms n Discussed Error Analysis n Preliminary timing simulations of timing look promising

Acknowledgements n Dr. Russell Duren n Dr. Michael Thompson

QUESTIONS?