Application Digital Logic Circuits Lecture 5 Section 1

Application: Digital Logic Circuits Lecture 5 Section 1. 4 Wed, Jan 24, 2007

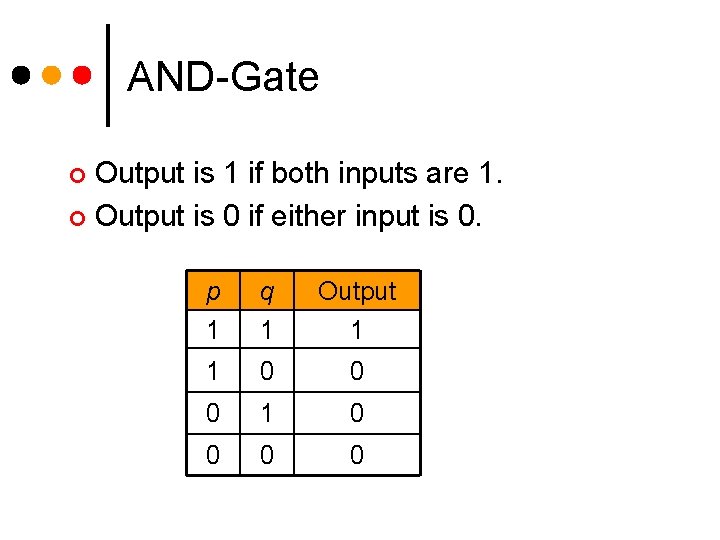
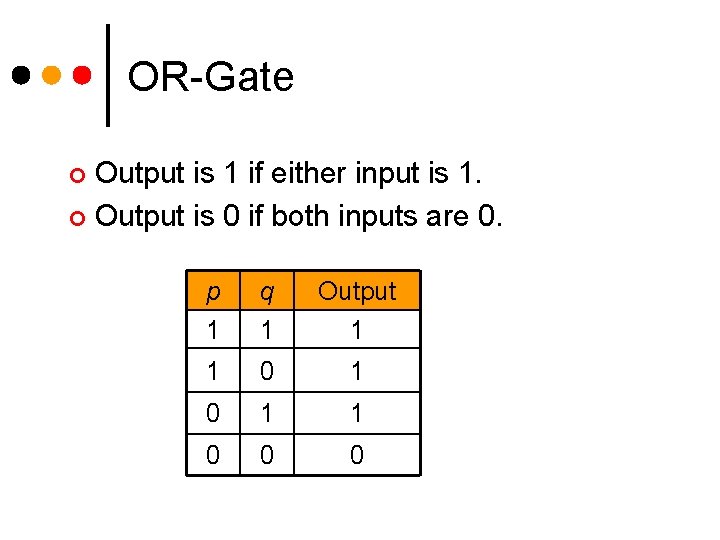
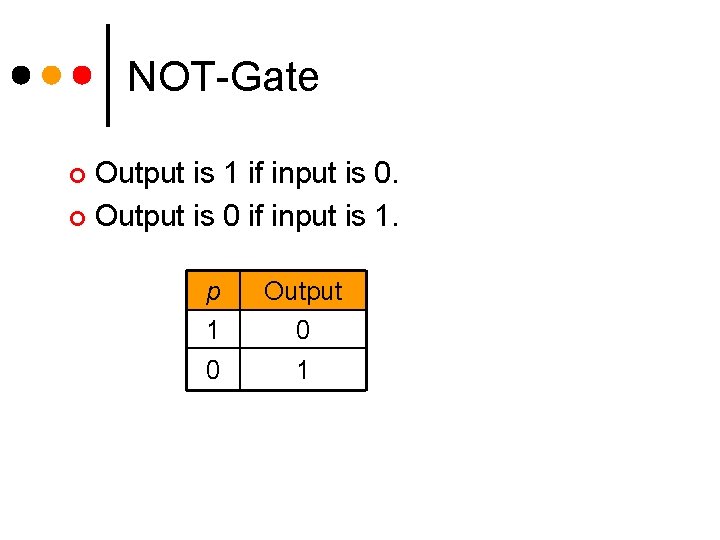
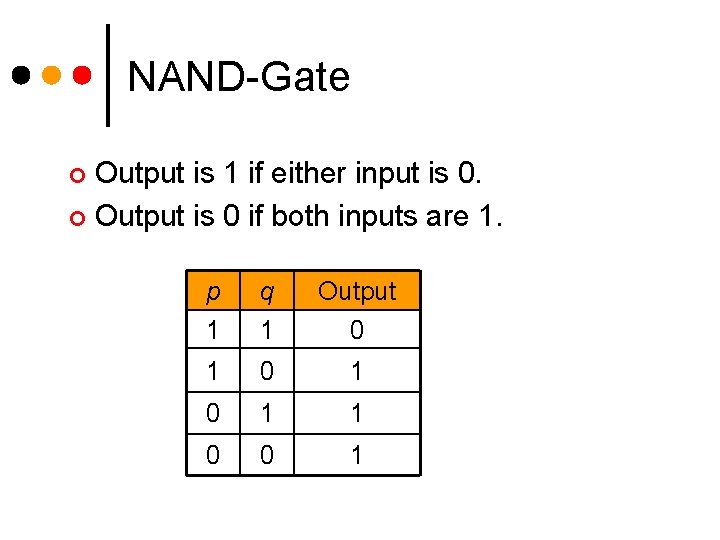
Logic Gates ¢ Three basic logic gates AND-gate l OR-gate l NOT-gate l ¢ Two other gates NAND-gate (NOT-AND) l NOR-gate (NOT-OR) l

AND-Gate Output is 1 if both inputs are 1. ¢ Output is 0 if either input is 0. ¢ p q Output 1 1 0 0 0 1 0 0

OR-Gate Output is 1 if either input is 1. ¢ Output is 0 if both inputs are 0. ¢ p q Output 1 1 0 0 0

NOT-Gate Output is 1 if input is 0. ¢ Output is 0 if input is 1. ¢ p Output 1 0 0 1

NAND-Gate Output is 1 if either input is 0. ¢ Output is 0 if both inputs are 1. ¢ p q Output 1 1 0 1 0 1 1 0 0 1

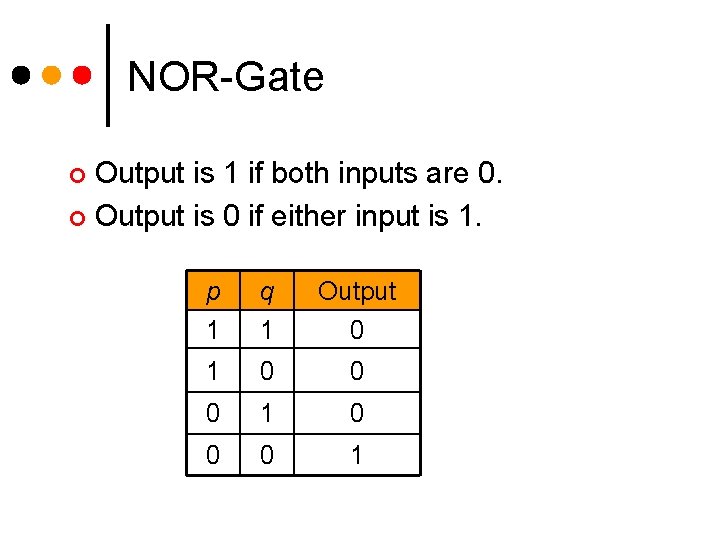
NOR-Gate Output is 1 if both inputs are 0. ¢ Output is 0 if either input is 1. ¢ p q Output 1 1 0 0 0 1

Disjunctive Normal Form ¢ A logical expression is in disjunctive normal form if It is a disjunction of clauses. l Each clause is a conjunction of variables and their negations. l Each variable or its negation appears in each clause exactly once. l

Examples: Disjunctive Normal Form p q (p q) ( p q). ¢ p | q (p q) ( p q). ¢ p q. ¢

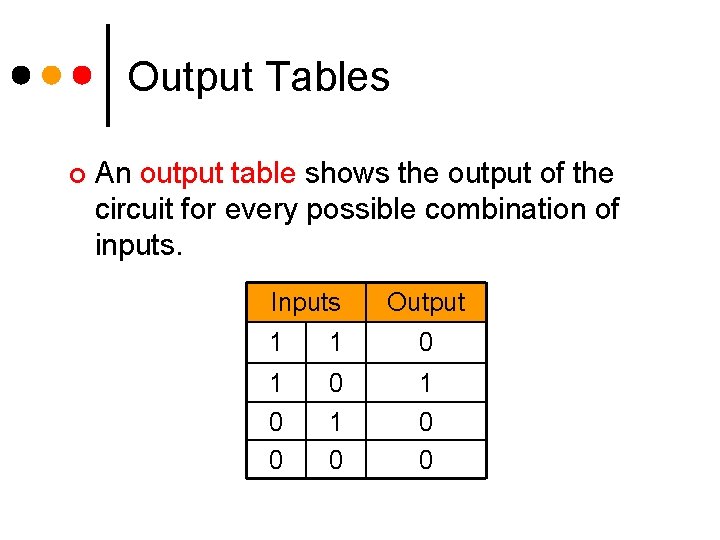
Output Tables ¢ An output table shows the output of the circuit for every possible combination of inputs. Inputs Output 1 1 0 0 0 1 0 0

Designing a Circuit Write an output table for the circuit. ¢ Write the expression in disjunctive normal form. ¢ Simplify the expression as much as possible. ¢ Write the circuit using AND-, OR-, and NOT-gates. ¢

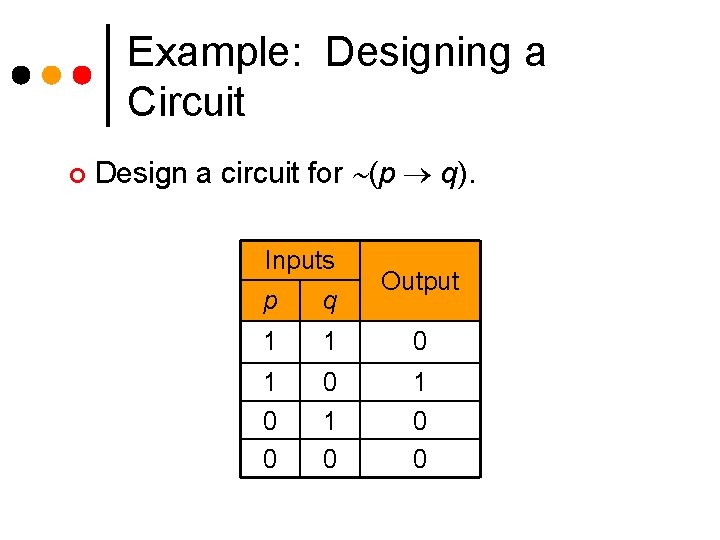
Example: Designing a Circuit ¢ Design a circuit for (p q). Inputs Output p q 1 1 0 0 0 1 0 0

Example: Designing a Circuit ¢ ¢ (p q) is equivalent to p q. Draw the circuit using an AND-gate and a NOT-gate.

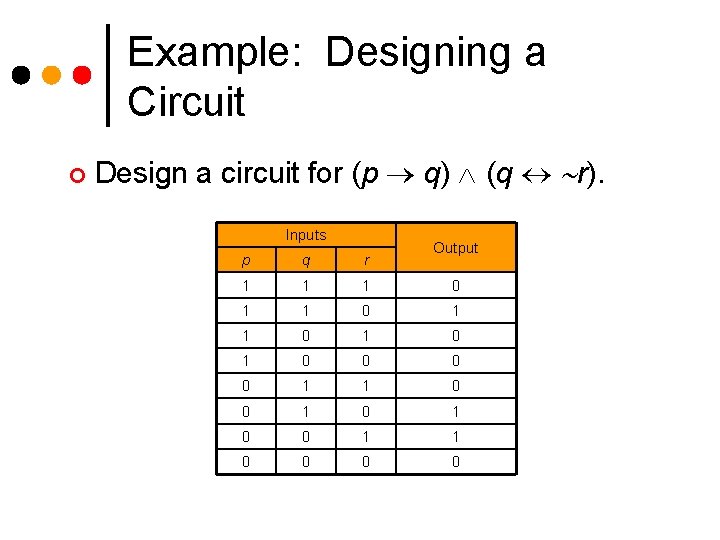
Example: Designing a Circuit ¢ Design a circuit for (p q) (q r). Inputs Output p q r 1 1 1 0 1 0 0 1 1 0 0

Example: Designing a Circuit (p q) (q r) is equivalent to (p q r) ( p q r). ¢ Does this simplify? ¢ In any case, we can draw a circuit, although it may not be optimal. ¢

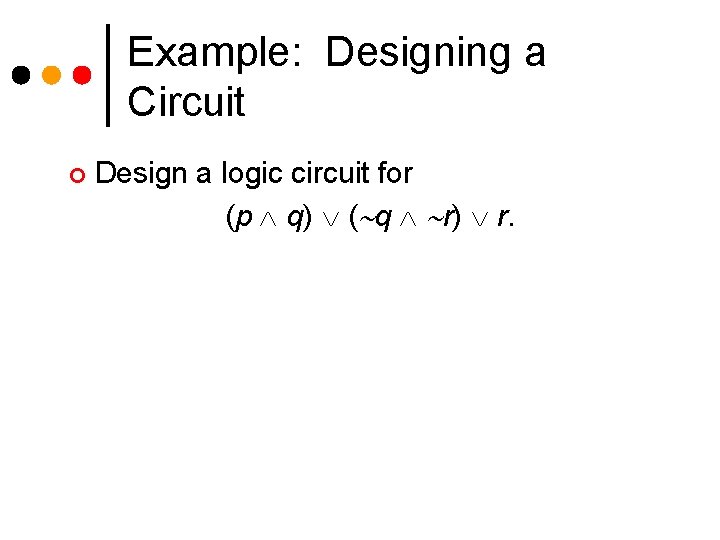
Example: Designing a Circuit ¢ Design a logic circuit for (p q) ( q r) r.

Conjunctive Normal Form ¢ A logical expression is in conjunctive normal form if It is a conjunction of clauses. l Each clause is a disjunction of variables and their negations. l Each variable or its negation appears in each clause exactly once. l

Examples: Conjunctive Normal Form p q. ¢ p q (p q) ( p q). ¢ p | q p q. ¢ p q (p q) ( p q). ¢

Conjunctive Normal Form ¢ To write an expression in CNF, Write the output table (truth table). l Follow the procedure for writing the expression in DNF, except l Reverse the rolls of 0 and 1 and . l

Example: Using CNF ¢ Re-do the previous example (p q) ( q r) r. using the conjunctive normal form.

The Red Dot-Blue Dot Puzzle ¢ ¢ ¢ Three men apply for a job. They are equally well qualified, so the employer needs a way to choose one. He tells them l l l “On the forehead of each of you I will put either a red dot or a blue dot. ” “At least one of you will have a red dot. ” “The first one who can tell me the color of the dot on his forehead gets the job. ”

The Red Dot-Blue Dot Puzzle The employer proceeds to put a red dot on each man’s forehead. ¢ After a few moments, one of them says, “I have a red dot. ” ¢ How did he know? ¢