Application Algorithms Lecture 17 Section 3 8 Thu

Application: Algorithms Lecture 17 Section 3. 8 Thu, Feb 16, 2006

Algorithms ¢ An algorithm is a step-by-step procedure that is guaranteed to stop after a finite number of steps for all legitimate inputs.

Example: Max Algorithm Describe an algorithm for finding the maximum value in a list of numbers. ¢ Special cases: ¢ What if the list is empty? l Others? l

An Algorithmic Language An algorithmic language is much like a computer language. ¢ Its primary purpose is to express unambiguously the steps of an algorithm, including all decisions and special cases that may arise. ¢

Assignment Statements ¢ An assignment statement is of the form x : = expr where x is a variable and expr is an expression. ¢ Examples found : = true l count : = count + 1 l

Conditional Statements ¢ One-way conditional statements: if condition then sequence of statements ¢ Two-way conditional statements: if condition then sequence of statements else sequence of statements

Iterative Statements ¢ While loops: while condition sequence of statements end while ¢ For loops: for var : = init expr to final expr sequence of statements next var

For Loops ¢ A for loop can always be rewritten as a while loop. var : = init expr while var final expr sequence of statements var : = var + 1 end while

A Notation for Algorithms ¢ An algorithm will be organized into three parts: Input – List all input variables and any special assumptions about them. l Algorithm body – Describe the step-by-step procedure. l Output – List the output variables. l

Example: Finding the Max ¢ Input: a, n a is a list of numbers. l n is the size of the list, n 1. l ¢ Algorithm body: ¢ Output: max : = a[1] for i : = 2 to n if a[i] > max then max = a[i] next i

Tracing an Algorithm ¢ Write a trace table for the Max algorithm and the input a = {7, 3, 8, 6, 4}, n = 5. Iteration a n max i 0 {7, 3, 8, 6, 4} 5 7 2 1 2 3 4

Tracing an Algorithm ¢ Write a trace table for the Max algorithm and the input a = {7, 3, 8, 6, 4}, n = 5. Iteration a n max i 0 {7, 3, 8, 6, 4} 5 7 2 7 3 1 2 3 4

Tracing an Algorithm ¢ Write a trace table for the Max algorithm and the input a = {7, 3, 8, 6, 4}, n = 5. Iteration a n max i 0 {7, 3, 8, 6, 4} 5 7 2 1 7 3 2 8 4 3 4

Tracing an Algorithm ¢ Write a trace table for the Max algorithm and the input a = {7, 3, 8, 6, 4}, n = 5. Iteration a n max i 0 {7, 3, 8, 6, 4} 5 7 2 1 7 3 2 8 4 3 8 5 4

Tracing an Algorithm ¢ Write a trace table for the Max algorithm and the input a = {7, 3, 8, 6, 4}, n = 5. Iteration a n max i 0 {7, 3, 8, 6, 4} 5 7 2 1 7 3 2 8 4 3 8 5 4 8 6

Greatest Common Divisors Let a and b be integers that are not both 0. ¢ The greatest common divisor of a and b, denoted gcd(a, b), is the unique positive integer d with the following properties: ¢ d | a and d | b. l For every integer c, if c | a and c | b, then c | d. l

Least Common Multiples Let a and b be nonzero integers. ¢ The least common multiple of a and b, denoted lcm(a, b), is the unique positive integer m with the following properties: ¢ a | m and b | m. l For every integer c, if a | c and b | c, then m | c. l

The High-school gcd Algorithm The high-school method is very inefficient. ¢ Factor each number into standard form. ¢ For each prime that appears in both factorizations, use it as a factor of the gcd along with the smaller of the two exponents. ¢

Example Find the gcd of 81900 and 54810. ¢ We factor them as ¢ 81900 = 22 32 52 71 131 290 l 54810 = 21 33 51 71 130 291 l ¢ Therefore, the gcd is l 2 32 5 7 = 630

The Euclidean Algorithm ¢ Factoring is inefficient; therefore, this algorithm is inefficient. l ¢ This algorithm is O( 10 d), where d is the number of digits in the number. Euclid had a much better idea. l Use the Euclidean Algorithm is O(d), where d is the number of digits in the number.

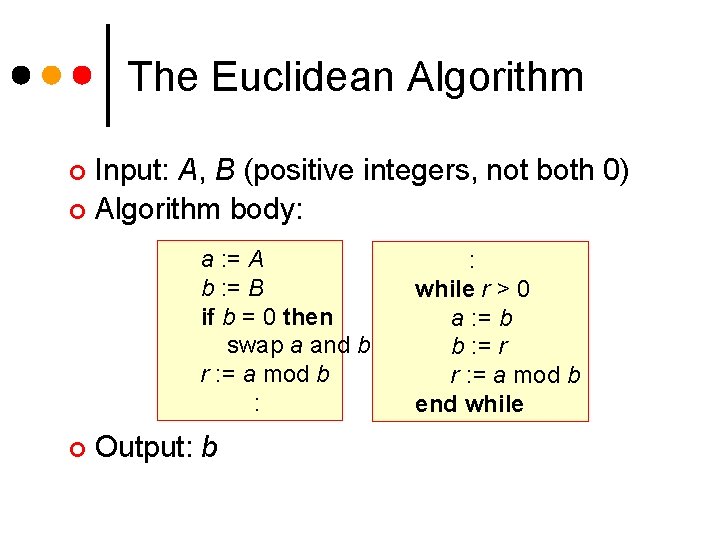
The Euclidean Algorithm Input: A, B (positive integers, not both 0) ¢ Algorithm body: ¢ a : = A b : = B if b = 0 then swap a and b r : = a mod b : ¢ Output: b : while r > 0 a : = b b : = r r : = a mod b end while

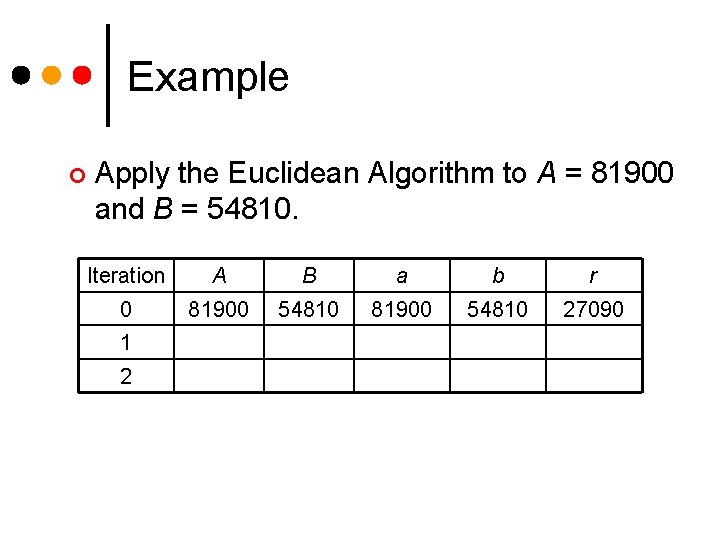
Example ¢ Apply the Euclidean Algorithm to A = 81900 and B = 54810. Iteration A B a b r 0 81900 54810 27090 1 2

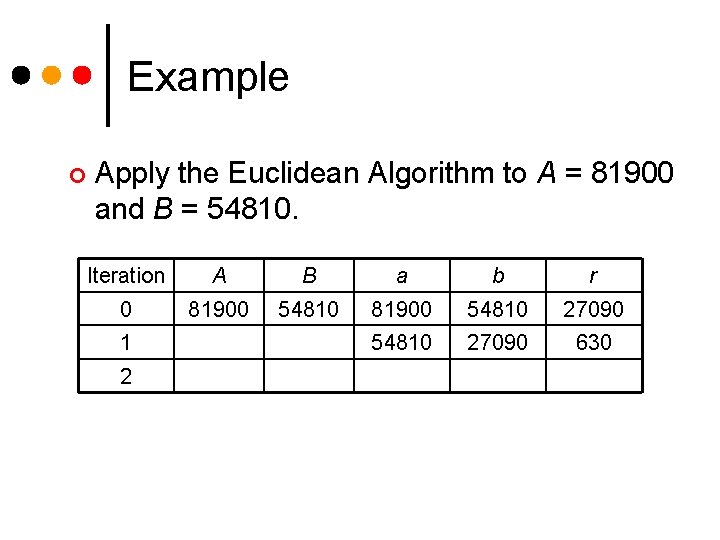
Example ¢ Apply the Euclidean Algorithm to A = 81900 and B = 54810. Iteration A B a b r 0 81900 54810 27090 630 1 2

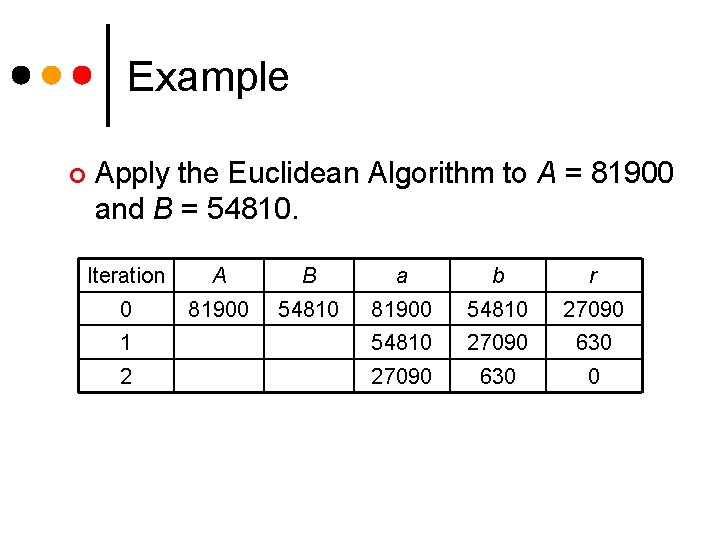
Example ¢ Apply the Euclidean Algorithm to A = 81900 and B = 54810. Iteration A B a b r 0 81900 54810 27090 1 54810 27090 630 2 27090 630 0

Least Common Multiples What is the efficient way to find lcm’s? ¢ What is the lcm of 81900 and 54810? ¢

Proof of the Euclidean Algorithm Theorem: The Euclidean Algorithm terminates for all legitimate inputs A and B. ¢ Proof: ¢ WOLOG, WMA B > 0. l After the first iteration of the while loop, 0 b<B since b is the remainder of A divided by B. l

Proof of the Euclidean Algorithm Each iteration produces a nonnegative remainder that is smaller than the previous remainder. l This cannot happen more than B times before the remainder is 0. l

Proof of the Euclidean Algorithm Lemma 1: If b > 0, then gcd(b, 0) = b. ¢ Proof: ¢ b | b and b | 0. l For all integers c, if c | 0 and c | b, then c | b. l Therefore, b = gcd(b, 0). l

Proof of the Euclidean Algorithm Lemma 2: If a and b are integers, with b 0, and q and r are integers such that a = qb + r then gcd(a, b) = gcd(b, r). ¢ Proof: ¢ Let d = gcd(b, r). l Then d | b and d | r and any integer that divides b and r must also divide d. l

Proof of the Euclidean Algorithm We must show that d | a and d | b and any integer that divides a and b must also divide d. l We already know that d | b. l Since a = qb + r, it follows that d | a. l Let c be an integer such that c | a and c | b. l Since r = a – qb, it follows that c | r and so c | d. l Therefore, d = gcd(a, b). l

Proof of the Euclidean Algorithm Theorem: The Euclidean Algorithm produces the gcd of A and B. ¢ Proof: ¢ After the final iteration of the while loop, r = 0. l By Lemma 1, the output b is the gcd of b and r. l By Lemma 2, that is equal to the gcd of “a” and “b” in the final iteration. l

Proof of the Euclidean Algorithm But “a” and “b” on the last iteration were “b” and “r” on the previous iteration. l Therefore, gcd(a, b) on the last iteration equals gcd(b, r) on the previous iteration, which equals gcd(a, b) on the previous iteration, and so on. l Following this argument all the back to the first iteration, we see that the output is gcd(A, B). l

Proof of the Euclidean Algorithm In a later chapter, we will study mathematical induction. ¢ At that point, we will be able to make this argument more rigorous. ¢