Appetizers What do you notice about these triangles

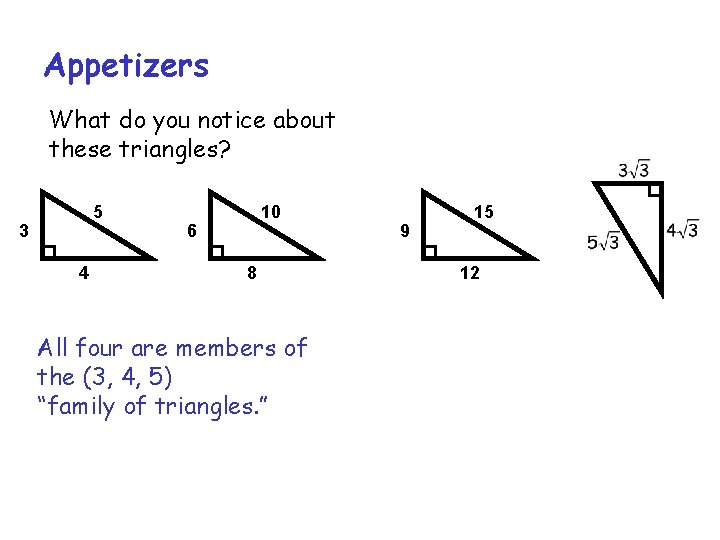
Appetizers What do you notice about these triangles? 5 3 4 10 6 8 All four are members of the (3, 4, 5) “family of triangles. ” 9 15 12

Chapter 7 Families of Right Triangles By the end of this lesson you will be able to *recognize Pythagorean triples *apply the Principle of the Reduced Triangle

Pythagorean Triples 5 3 Definition: Any three whole numbers that satisfy the equation a 2 + b 2 = c 2 form a Pythagorean triple. (3, 4, 5) are Pythagorean triples (6, 8, 10) are Pythagorean triples (9, 12, 15) are Pythagorean triples ( , , ) are NOT Pythagorean triples. Why not? They are not whole numbers. 6 4 9 10 8 15 12

Pythagorean Triples (cont. ) There are infinitely many families. Some common families are: (5, 12, 13) OR (15, 36, 39) (7, 24, 25) OR (14, 48, 50) (8, 15, 17) OR (4, 7½, 8½) The GREATEST number is the hypotenuse, NOT the third number! 24 7 x NOTE: Problems involving Pythagorean triples frequently appear on standardized tests. Don’t be fooled. You may think the answer is 25 from the family (7, 24, 25), but 25 represents the hypotenuse! You are stuck with the long way to solve the problem!

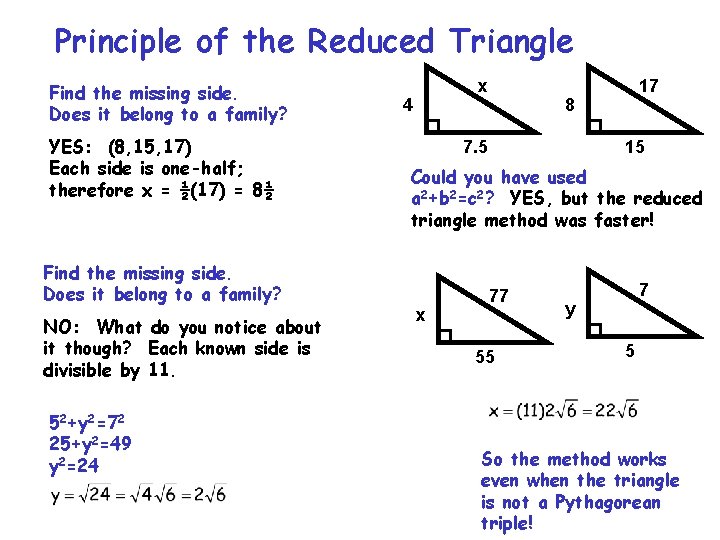
Principle of the Reduced Triangle Find the missing side. Does it belong to a family? YES: (8, 15, 17) Each side is one-half; therefore x = ½(17) = 8½ Find the missing side. Does it belong to a family? NO: What do you notice about it though? Each known side is divisible by 11. 52+y 2=72 25+y 2=49 y 2=24 x 4 17 8 7. 5 15 Could you have used a 2+b 2=c 2? YES, but the reduced triangle method was faster! x 77 55 7 y 5 So the method works even when the triangle is not a Pythagorean triple!

Principle of the Reduced Triangle 1. Reduce the level of difficulty of the problem by multiplying or dividing the three sides of the triangle by the same number to obtain a similar, but simpler, triangle in the same family. 2. Solve for the missing side of the easier triangle. 3. Convert back to the original problem.