APPENDIX B Transformation of RV Functional Transformation of

APPENDIX B Transformation of RV Ø Ø Functional Transformation of RV Sinusoidal Transformation Diode characteristic Rayleigh distribution Huseyin Bilgekul EEE 461 Communication Systems II Department of Electrical and Electronic Engineering Eastern Mediterranean University EEE 461 1

Homework Assignment I • Homework Problems • B-5, B-7, B 10, B-26, B-32 • To be returned 25 October 2005 EEE 461 2

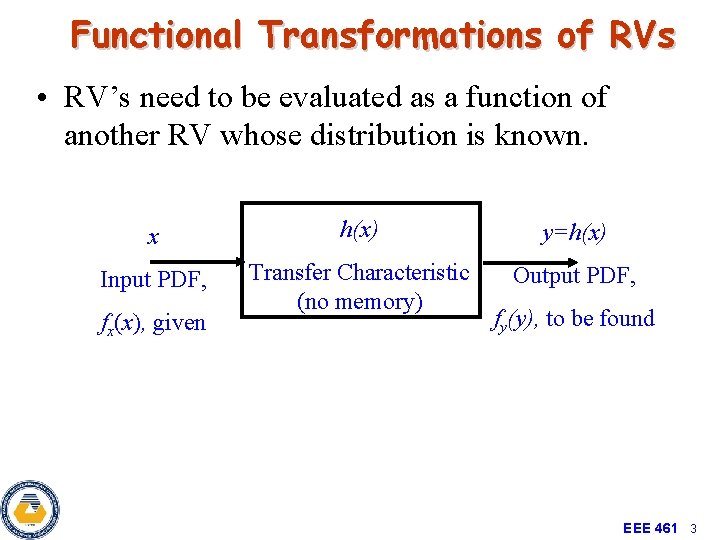
Functional Transformations of RVs • RV’s need to be evaluated as a function of another RV whose distribution is known. x h(x) y=h(x) Input PDF, Transfer Characteristic (no memory) Output PDF, fx(x), given fy(y), to be found EEE 461 3

Transformation of RVs-Finding f. Y(y) • Define an event around a point y, over a small interval increment, dy. • – This used rectangle area approximation, and is exact for incremental dy. • The inverse image of this event in Y maps to an even X with the same probability. EEE 461 4

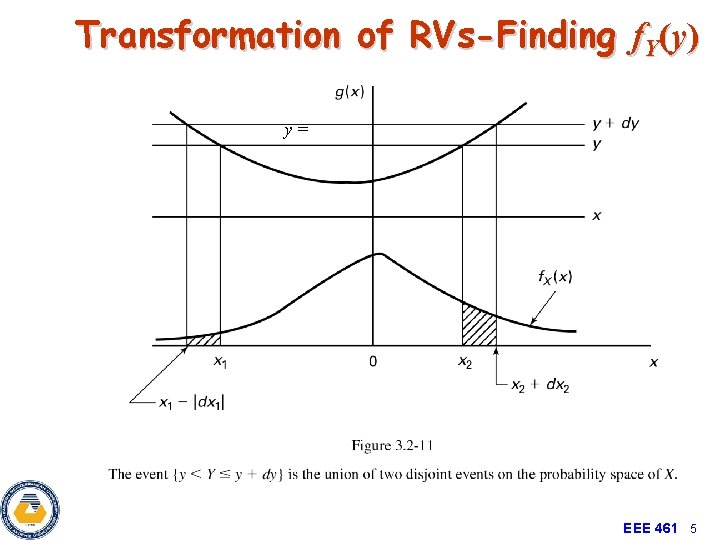
Transformation of RVs-Finding f. Y(y) y= EEE 461 5

Transformation of RVs-Finding f. Y(y) • Points between y and y+dy map in this example to 2 corresponding segments in x, thus the corresponding event is disjoint: • Therefore: EEE 461 6

Transformation of RVs-Finding f. Y(y) PDF after transformation y= Transformation of y=g(x) EEE 461 7

Transforming RVs • Theorem: If y=h(x) where h( ) is the transfer function of a memoryless device, Then the PDF of the output, y is: – fx(x) is the PDF of the input. – M is the number of real roots of y=h(x), which means that the inverse of y=h(x) gives x 1, x 2, . . . , x. M for a single value of y. Single vertical line denotes the evaluation of the quantity at EEE 461 8

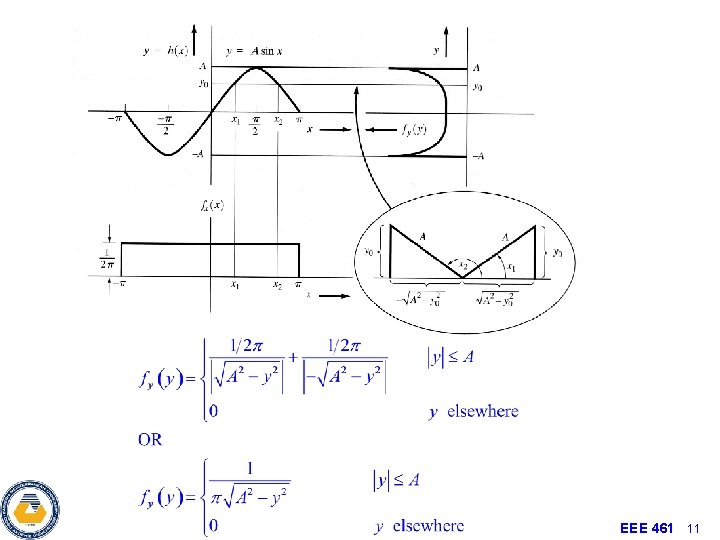
Example Sinusoidal Distribution • Let • x is uniformly distributed from –π to π. What is the PDF of y Output PDF Input PDF EEE 461 9

Example Sinusoidal Distribution • For some value of y, say y 0, there are two possible values of x, say x 1 and x 2 • Simplify by replacing pdf of x with fx(x)=1/2 p • Evaluating cosine terms, see figure EEE 461 10

EEE 461 11

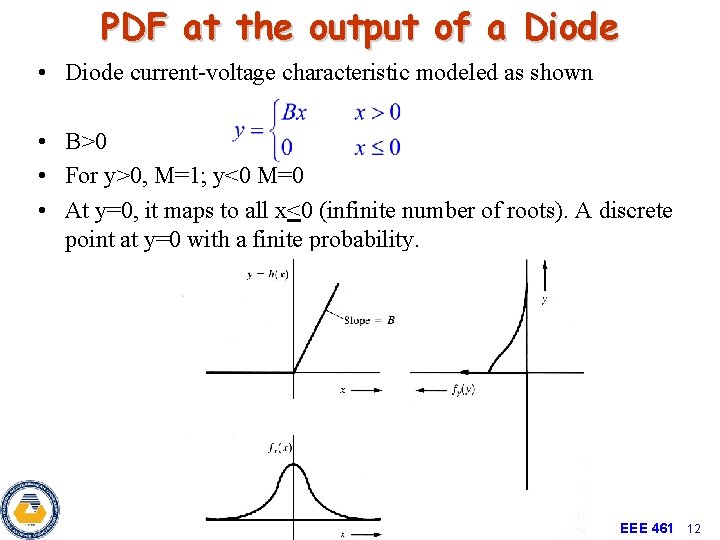
PDF at the output of a Diode • Diode current-voltage characteristic modeled as shown • B>0 • For y>0, M=1; y<0 M=0 • At y=0, it maps to all x<0 (infinite number of roots). A discrete point at y=0 with a finite probability. EEE 461 12

PDF at the output of a Diode • For y>0, M=1; y<0 M=0 • At y=0, it maps to all x<0 (infinite number of roots). A discrete point at y=0 with a finite probability. EEE 461 13

Exercise 1 1. y=Kx • X is normal, N(0, sx 2) • Find the pdf of y EEE 461 14

Dart Board • Randomly throw darts at a dart board • More likely to throw darts in center each coordinate is a Gaussian RV y x EEE 461 15

Rayleigh Distribution • Given two independent, identically distributed (IID) Gaussian RVs, x and y: • Find the PDFs of the amplitude and phase of these variables (polar coordinates): EEE 461 16

Rayleigh Distribution • Joint density of x and y is: • Transform from (x, y) to polar coordinates: EEE 461 17

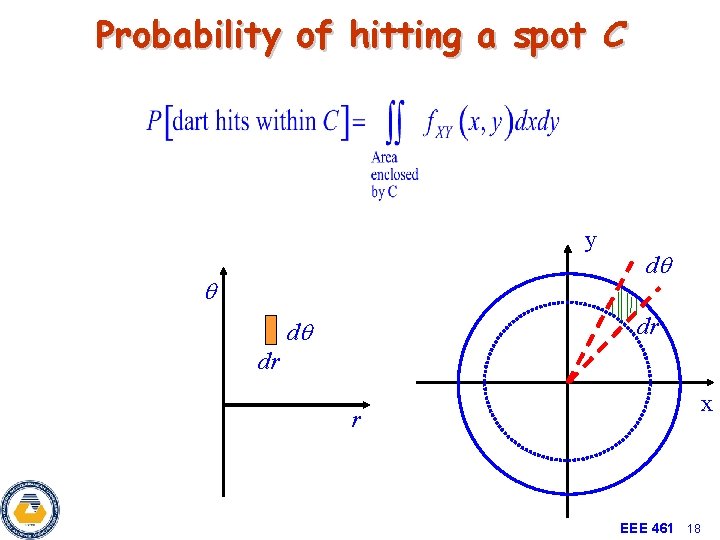
Probability of hitting a spot C y q dq dr x r EEE 461 18

Rayleigh Distribution • From calculus recall that this integral can be converted to polar coordinates: EEE 461 19

Rayleigh Distribution • Relationship between density functions is: EEE 461 20

Change Coordinates • Relationship between density functions is: Take the joint distribution and integrate out one of the variables to obtain MARGINAL DENSITIES. EEE 461 21

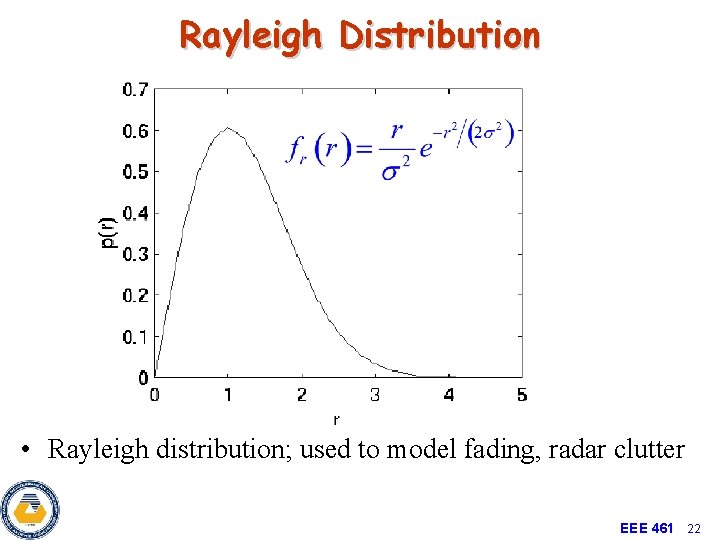
Rayleigh Distribution • Rayleigh distribution; used to model fading, radar clutter EEE 461 22

Exercise 2 1. y=x 2 • Find the pdf of y • X is normal, N(0, sx 2) EEE 461 23