APLICACIONES DE LAS DERIVADAS Por Jorge Snchez MONOTONA

APLICACIONES DE LAS DERIVADAS Por Jorge Sánchez

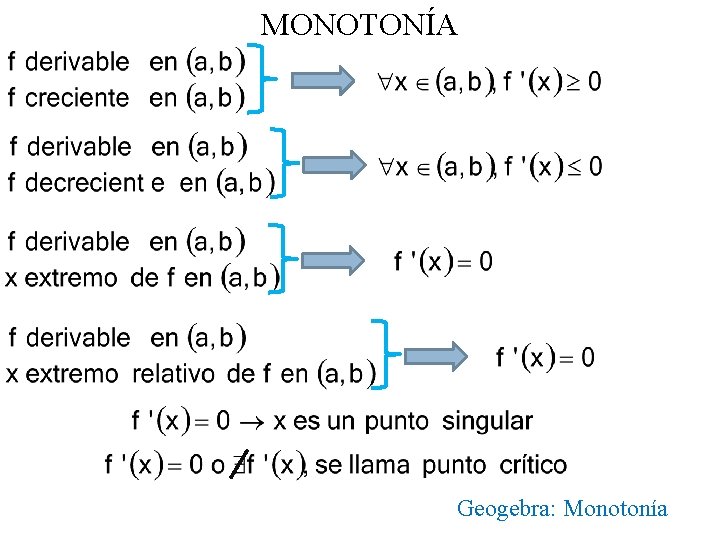
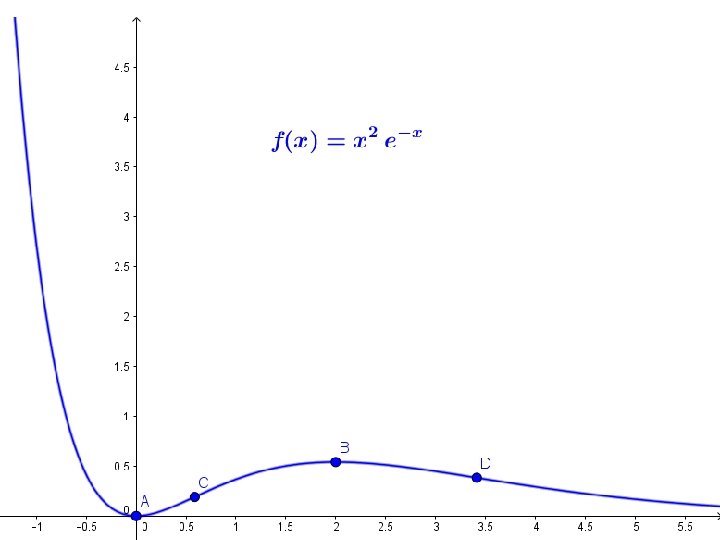
MONOTONÍA Geogebra: Monotonía

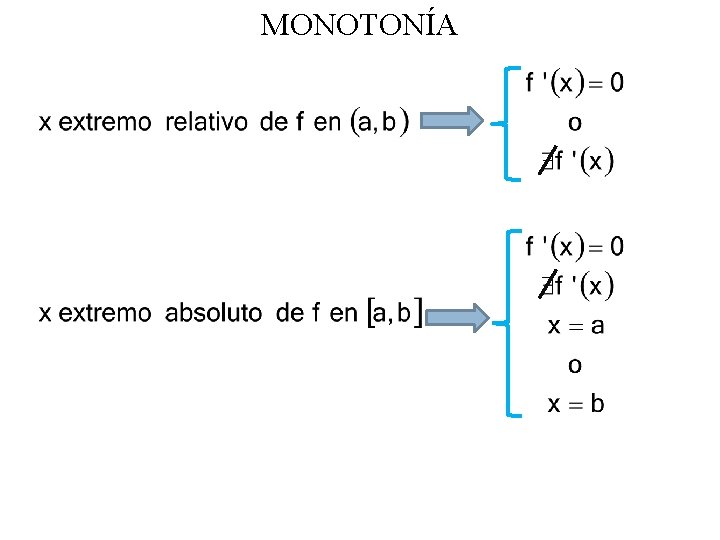
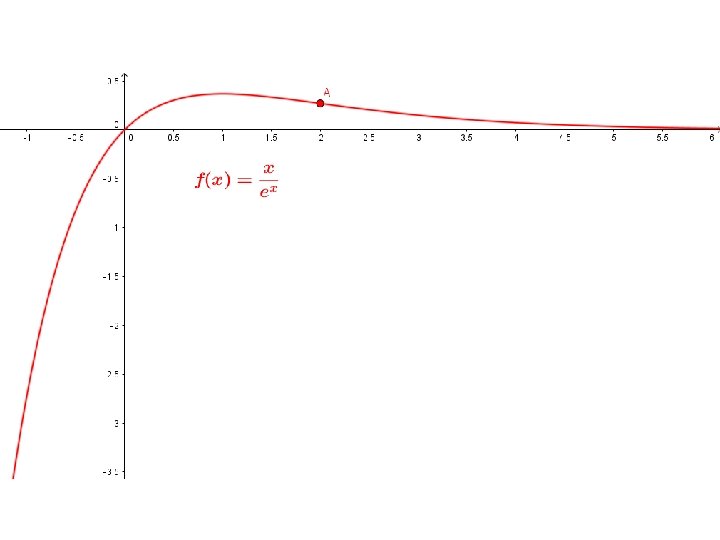
MONOTONÍA

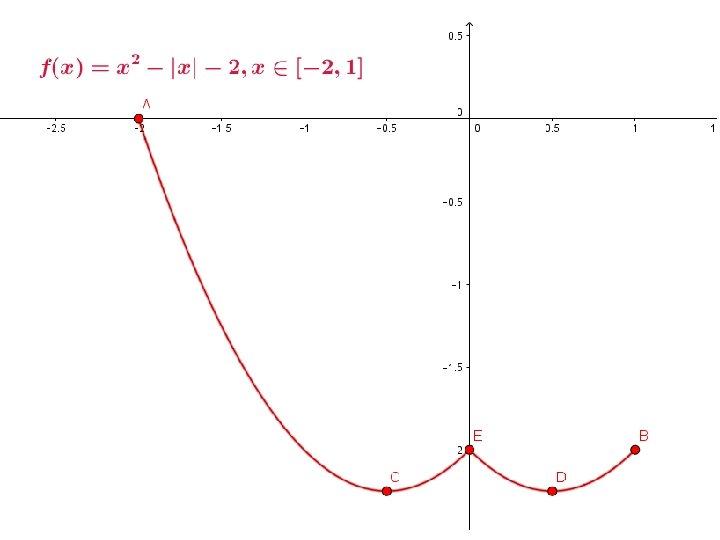
Actividad 2 de la página 238 v, 234 n

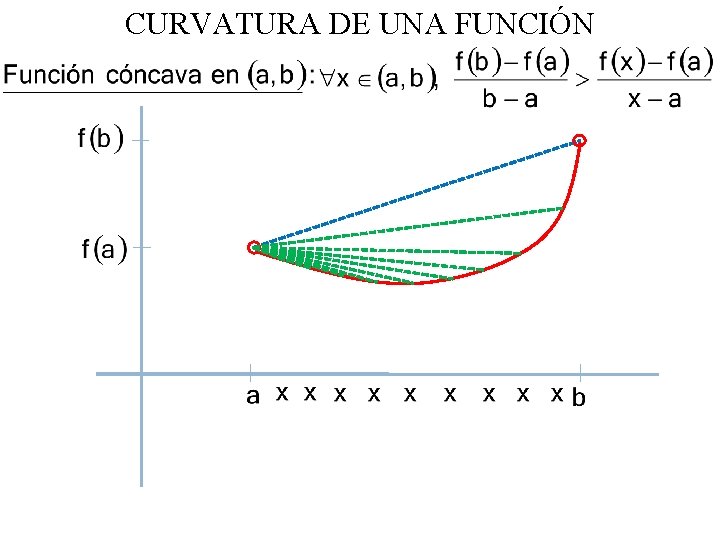
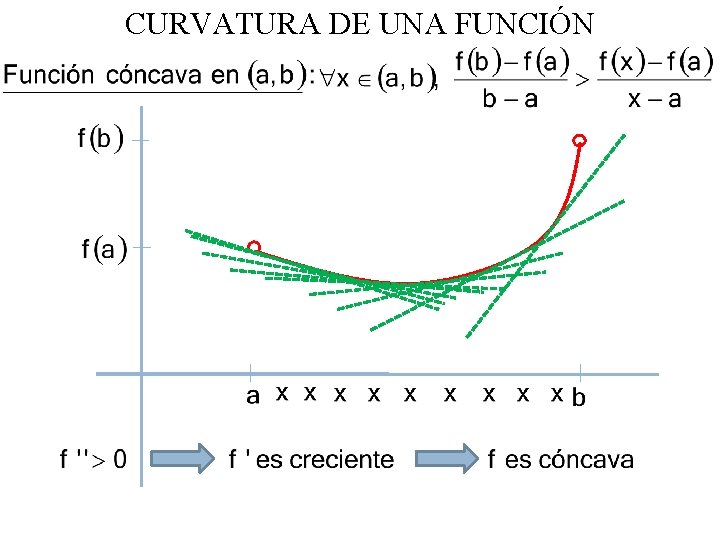
CURVATURA DE UNA FUNCIÓN

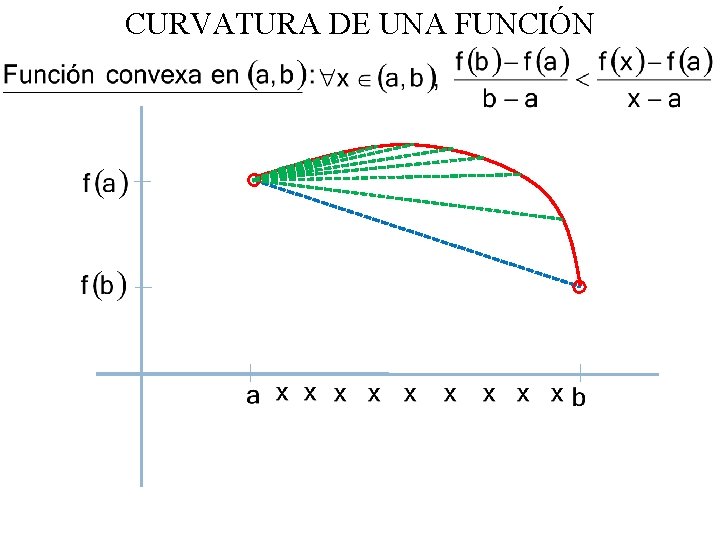
CURVATURA DE UNA FUNCIÓN

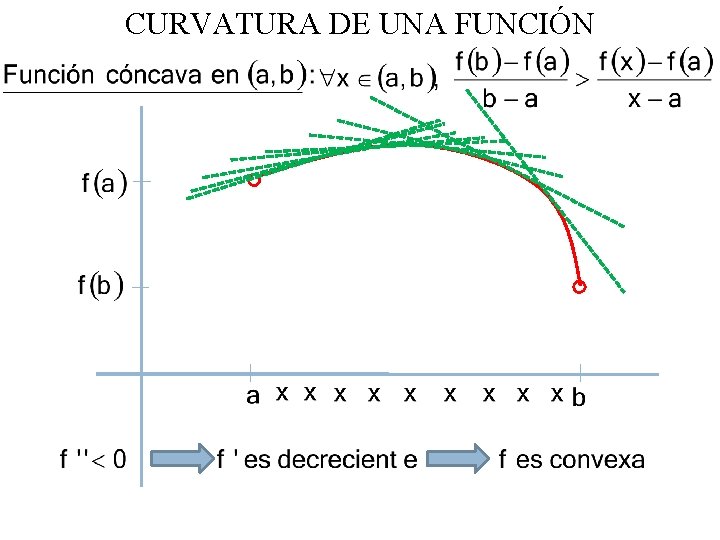
CURVATURA DE UNA FUNCIÓN

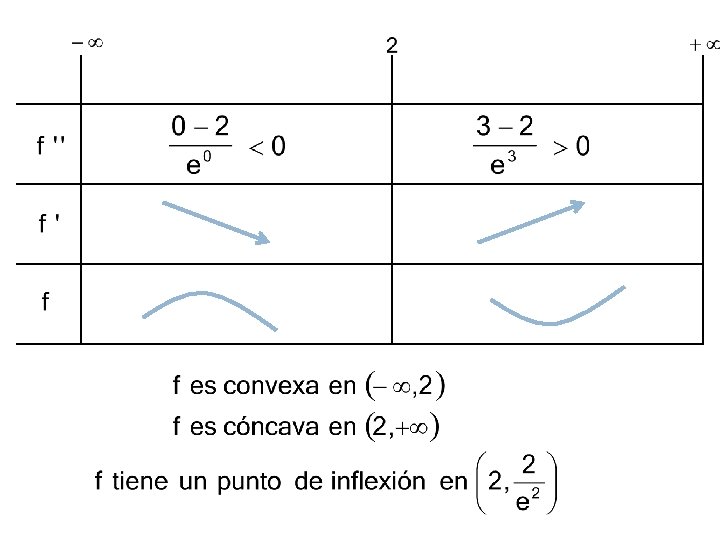
CURVATURA DE UNA FUNCIÓN

CURVATURA DE UNA FUNCIÓN Geogebra: Curvatura

Actividad 4 b); 13 b) de la página 248 v, 4 b) de 236 n

EJERCICIOS PARA CASA Actividad 4 g)

TEOREMA DE ROLLE Michel Rolle (21 de abril de 1652 - 8 de noviembre de 1719) Matemático francés nacido en Ambert

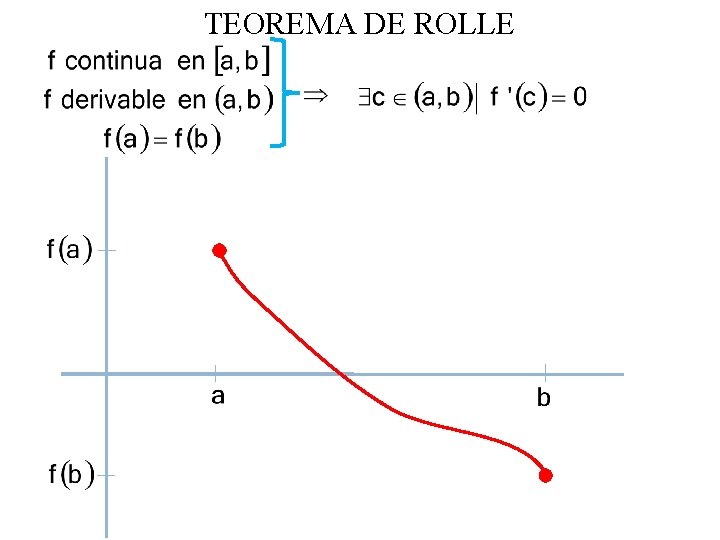
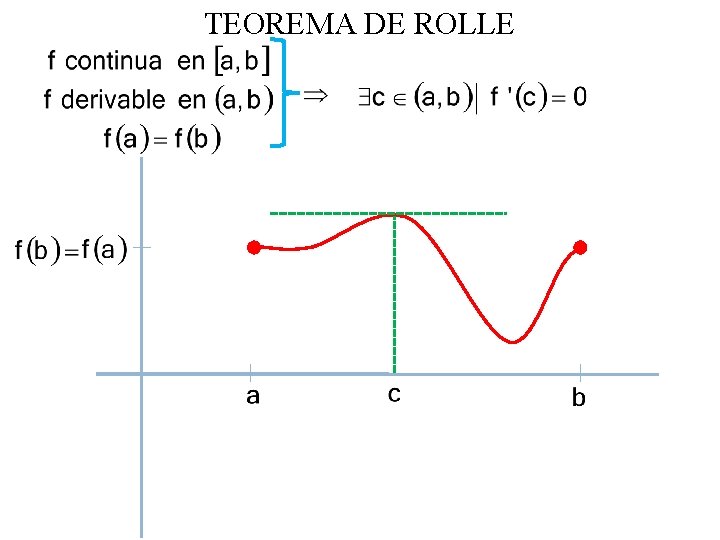
TEOREMA DE ROLLE

TEOREMA DE ROLLE

EJERCICIOS PARA CASA Actividad 6

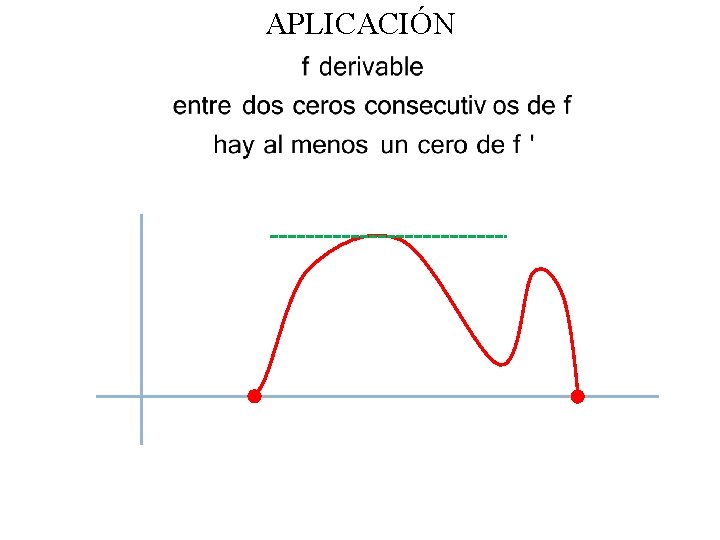
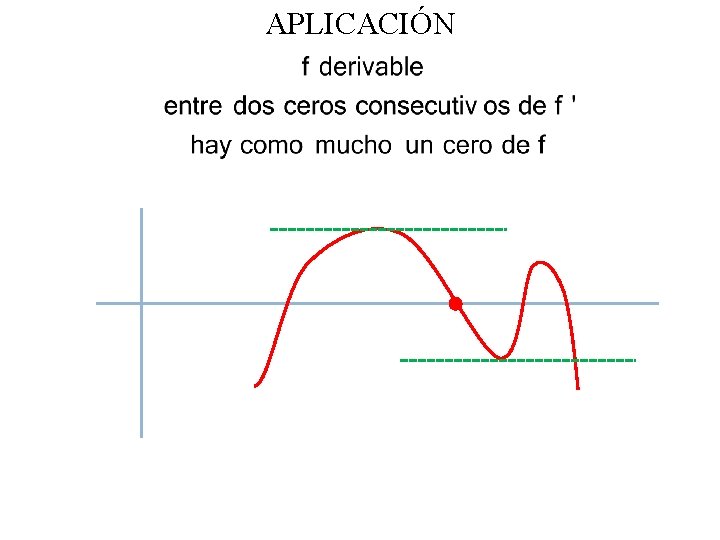
APLICACIÓN

APLICACIÓN

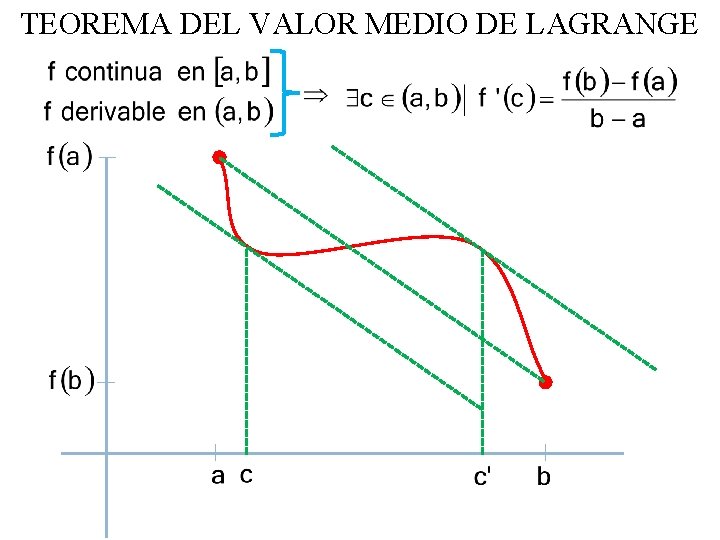
TEOREMA DEL VALOR MEDIO DE LAGRANGE Giuseppe Lodovico Lagrangia (25 de enero de 1736 - 10 de abril de 1813) Matemático italiano nacido en Turín

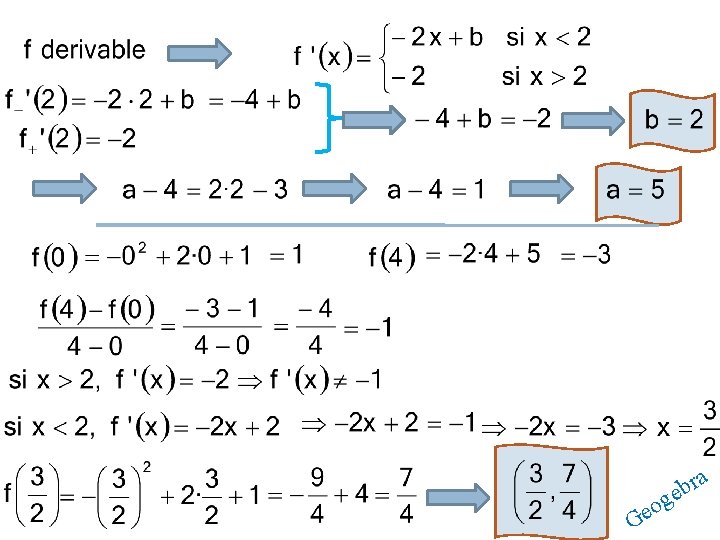
TEOREMA DEL VALOR MEDIO DE LAGRANGE

Actividad 12; 11 de la página 242 v, 12 de 240 n

og e G ra b e

EJERCICIOS PARA CASA Actividad 11

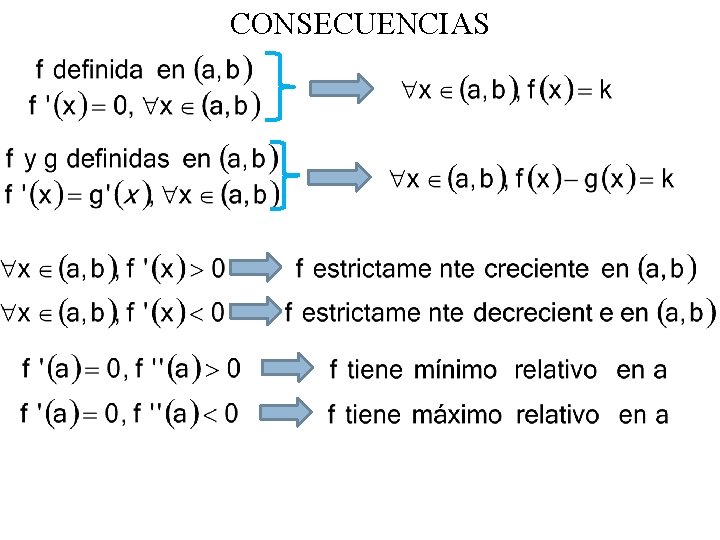
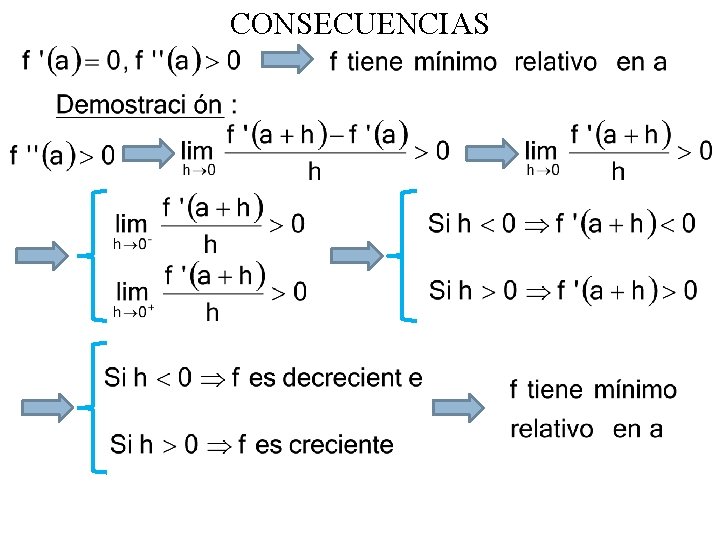
CONSECUENCIAS

CONSECUENCIAS

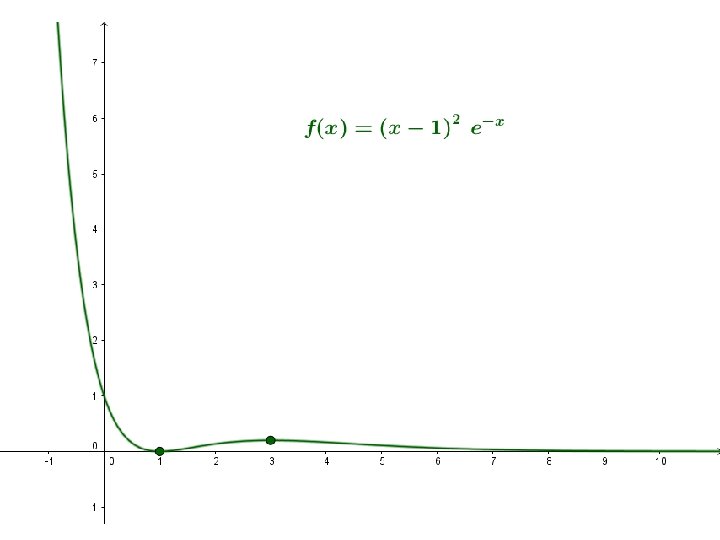
MÁXIMOS, MÍNIMOS Y PUNTOS DE INFLEXIÓN

Actividad 29; 36 de la página 257 v, 4 de 257 n

EJERCICIOS PARA CASA Actividad 13 a) y e)

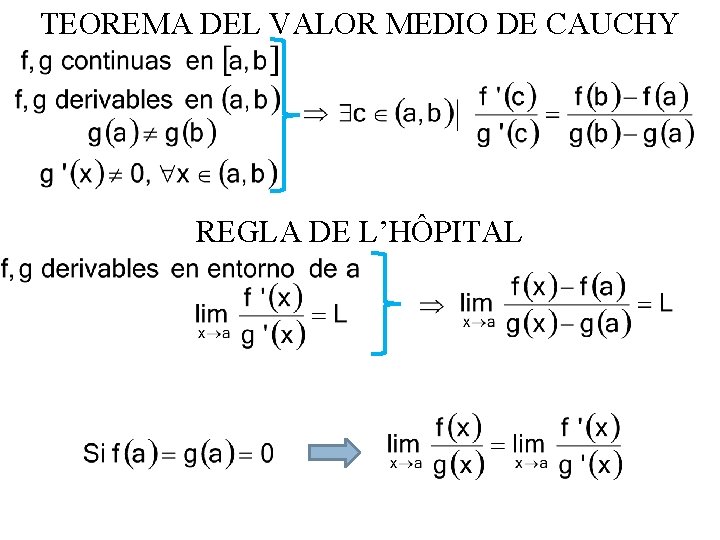
TEOREMA DEL VALOR MEDIO DE CAUCHY Augustin Louis Cauchy (21 de agosto de 1789 - 23 de mayo de 1857) Matemático francés nacido en París

TEOREMA DEL VALOR MEDIO DE CAUCHY REGLA DE L’HÔPITAL Guillaume François Antoine, marqués de l'Hôpital (1661 - 2 de febrero de 1704) Matemático francés nacido en París

TEOREMA DEL VALOR MEDIO DE CAUCHY REGLA DE L’HÔPITAL

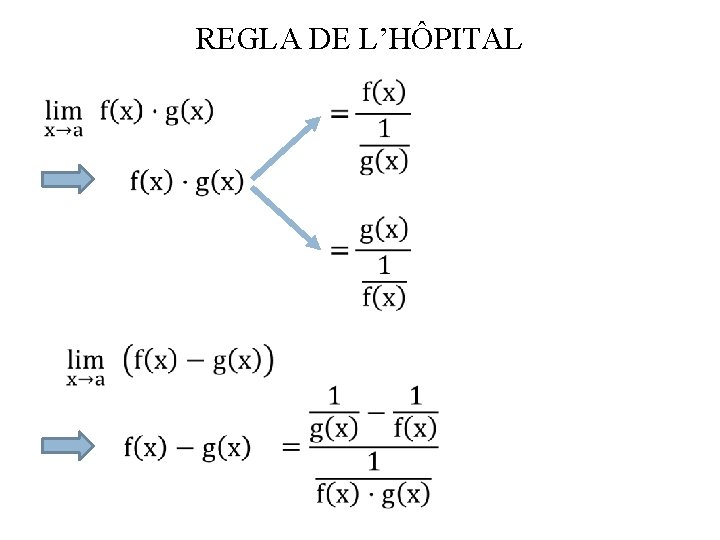
REGLA DE L’HÔPITAL

Actividad 14 b); 15 b) de la página 251 v, 14 b) de 245 n

EJERCICIOS PARA CASA Actividad 14 Todos menos b)

REPRESENTACIÓN GRÁFICA DE FUNCIONES

EJERCICIOS PARA CASA Actividad 95 a) y c)

OPTIMIZACIÓN 1. 6. 7. Poner letras (x, y, h, t, …) a las variables que intervienen en el problema Poner cuál es la función que tenemos que optimizar (maximizar o minimizar) Si solo hay una variable pasar al paso 6 Si hay varias variables buscar relaciones entre ellas Despejar variables y sustituir en la función de manera que solo quede una variable Derivar la función Igualar a cero la derivada y resolver 8. Comprobar que la solución es lo que se pide (máximo o mínimo) 2. 3. 4. 5. 9. Si solo hay una variable pasar al paso 11 10. Sustituir el resultado en las relaciones para hallar el valor del resto de variables si es necesario 11. Contestar a las preguntas del problema

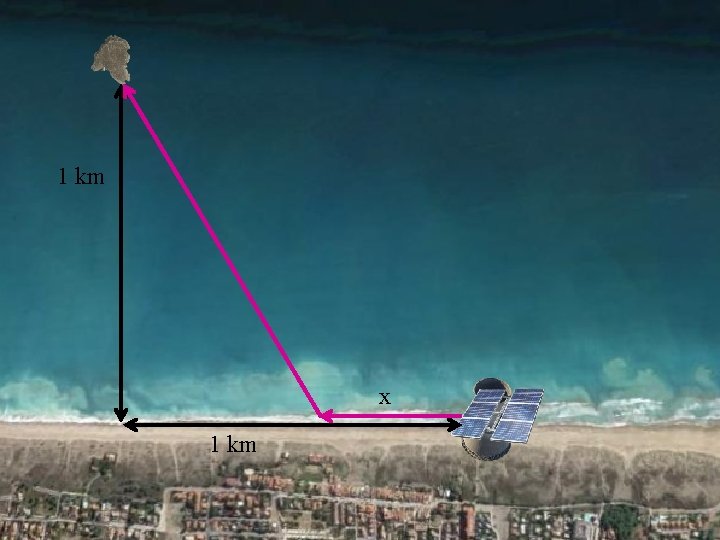
OPTIMIZACIÓN Actividad 80; 33 de la página 287 v, 55 de 260 n Un pequeño islote dista 1 km de una costa rectilínea. Se quiere instalar en dicho islote una señal luminosa que se ha de alimentar con un tendido eléctrico. La fuente de energía está situada en la costa, en un punto distante 1 km del punto de la costa más próximo al islote. El coste del tendido submarino por unidad de longitud es 5/3 del tendido en tierra. ¿A qué distancia de la fuente de energía debe empezar el tendido submarino para conseguir un coste mínimo?

1 km x 1 km

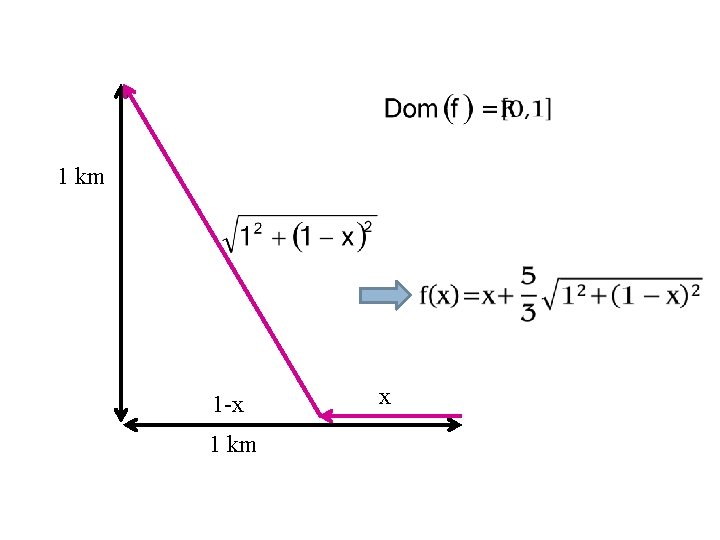
1 km 1 -x 1 km x

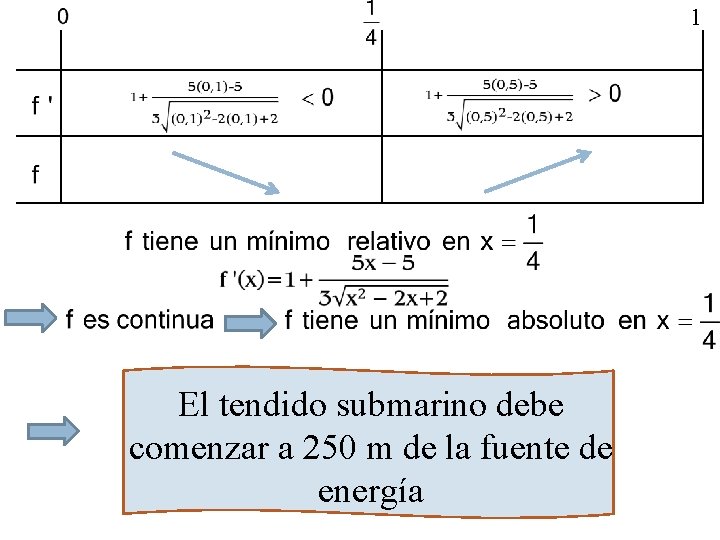
1 El tendido submarino debe comenzar a 250 m de la fuente de energía

Para que los ingresos de ese día sean máximos se debe vender 1 tonelada de acero de baja calidad y 2 toneladas de acero de alta calidad

El ingreso máximo que se puede obtener por las ventas de acero en un día es de 2100 €

EJERCICIOS PARA CASA Actividad 15 Actividad 16 Actividad 19

EJERCICIOS PARA CASA Actividad 46

EJERCICIOS PARA CASA Actividad 63 Actividad 73

EJERCICIOS PARA CASA Actividad 79 Geogebra