AP STATISTICS LESSON 3 3 LEAST SQUARES REGRESSION

AP STATISTICS LESSON 3 – 3 LEAST – SQUARES REGRESSION

Regression Line l. A regression line is a straight line that describes how a response variable y changes as an explanatory variable x changes. We often use a regression line to predict the value of y for a given value of x. Regression, unlike correlation, requires we have an explanatory variable and a response variable. l LSRL – Is the abbreviation for least squares regression line. LSRL is a mathematical model.

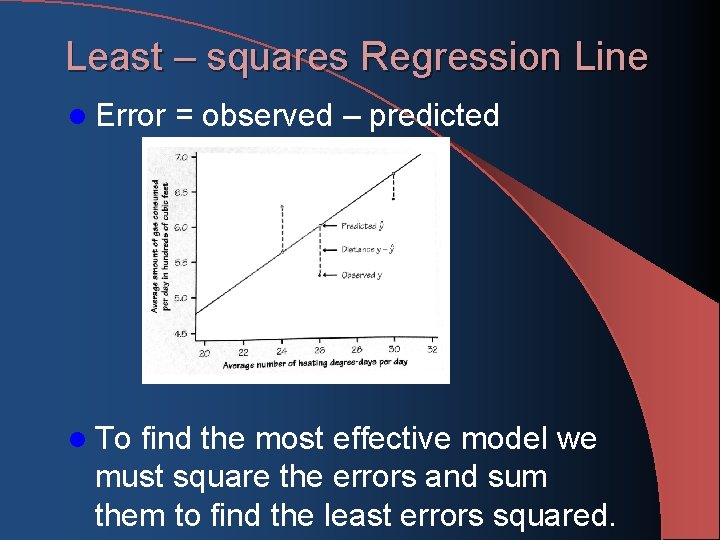
Least – squares Regression Line l Error l To = observed – predicted find the most effective model we must square the errors and sum them to find the least errors squared.

Least – squares Regression Line l The least – squares regression line of y on x is the line that makes the sum of the squares of the vertical distances of the data points from the line as small as possible.

Equation of the LSRL l We have data on an explanatory variable x and a response variable y for n individuals. From the data, calculate the means ¯x and y¯ and the standard deviations sx and sy, and their correlation r.

What happened to y = mx+b? ly represents the observed (actual) values for y, and yˆ represents the predicted values for y. We use y hat in the equation of the regression line to emphasize that the line gives predicted values for any x. l When you are solving regression problems, ˆ be sure to distinguish between y and y. ¯¯ Hot tip: (x, y) is always a point on the regression line!

AP STATISTICS LESSON 3 – 3 (DAY 2) The role of r 2 in regression

Essential Question: How is the r 2 used to determine the reliability of a linear regression line? l To calculate r 2. find the SST, the SSE and find the r 2 from them.

Definitions and Abbreviations r 2 = coefficient of determination ( The proportion of the total sample variability that is explained by the least-squares regression of y on x. LSRL – Least squares regression line. SST – (Total Sum of Squares) 2 SST = ∑ ( y – y ) SSE – (Sum of squares of errors) 2 SSE = ∑ ( y – ŷ)

Exercises Small r 2 and Large r 2 Page 158: Example 3. 10 SMALL r 2 Page 160: Example 3. 11 LARGE r 2

r 2 in Regression The coefficient of determination r 2, is the fraction of the variation in the values of y that is explained by least-squares regression of y on x. r 2 = SST - SSE SST

Facts about Least-squares Regressions l Fact 1: The distinction between explanatory and response variable is essential in regression. l Fact 2: There is a close connection between correlation and the slope of the least-squares line. A change of one standard deviation of x corresponds to a change of r standard deviations in y.

Facts of Regression (continued) l Fact 3. The least-squares regression line always passes through the point ( x, y ). l Fact 4. The square of the correlation, r 2, is the fraction of the variation in the values of y that is explained by the least -squares regression of y on x.

A P STATISTICS LESSON 3 – 3 (DAY 3) RESIDUALS

ESSENTIAL QUESTION: What is a residual and what can a residual graph tell us about linear regression lines? Objective: To define and use residuals in the analysis of linear regression lines.

Residuals l. A residual is the difference between an observed variable and the value predicted by the regression line. That is, residual = observed y – predicted y =y-ŷ

Residual Facts l The mean of the least-square residuals is always zero. l The sum is not exactly 0 because the software rounded the residuals to four decimal places. l This is roundoff error. l The horizontal line of the residual plot is at zero.

Residual Plots l A residual plot is a scatterplot of the regression residuals against the explanatory variable. Residual plots help us assess the fit of a regression line. l If the regression line captures the overall relationship between x and y, the residuals should have no systematic pattern. The residual plot will look something like the simplfied pattern. That plot shows a uniform scatter of the points about the fitted line, with no unusual individual observations.