AP Physics Unit 7 Part 1 Rotational Kinematics

AP Physics Unit 7 Part 1 Rotational Kinematics Textbook 7. 1 Angular Measure Textbook 7. 2 Angular Speed and Velocity Textbook 7. 4 Angular Acceleration

7. 1 Angular Measure

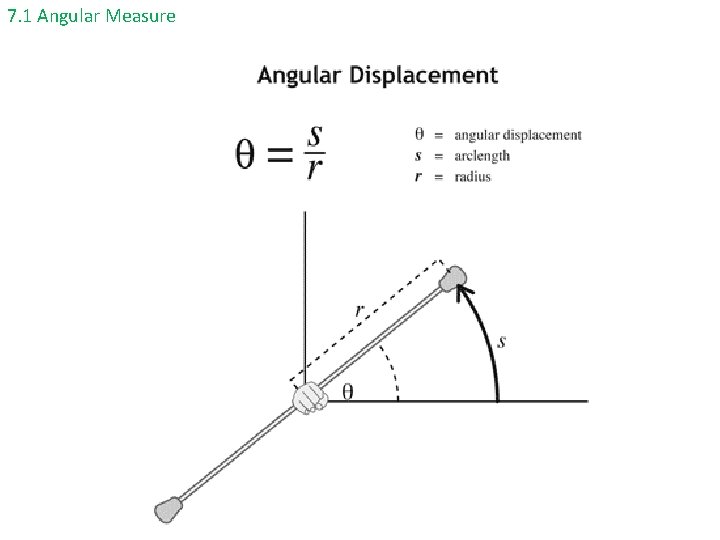
7. 1 Angular Measure rotation – axis of rotation lies within the body (example: Earth rotates on its axis) The object spins. revolution – axis of rotation lies outside the body (example: Earth revolves around the Sun). The object moves around another object in a circle. • Circular motion is conveniently described using polar coordinates (r, Ө) because r is a constant and only Ө varies. • Ө is measured counter-clockwise from the +x axis. The relationship between rectangular coordinates and polar coordinates are: x = r cos Ө y = r sin Ө

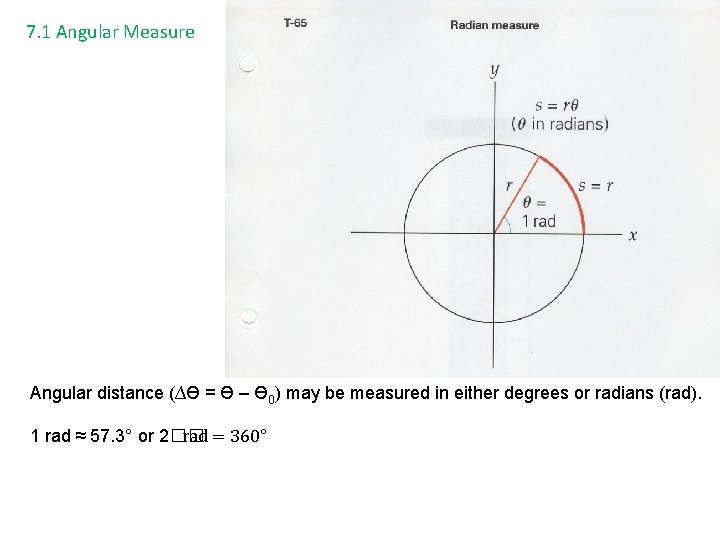
7. 1 Angular Measure Angular distance (∆Ө = Ө – Ө 0) may be measured in either degrees or radians (rad). 1 rad ≈ 57. 3° or 2�� rad = 360°

7. 1 Angular Measure

7. 1 Angular Measure

7. 2 Angular Speed and Velocity

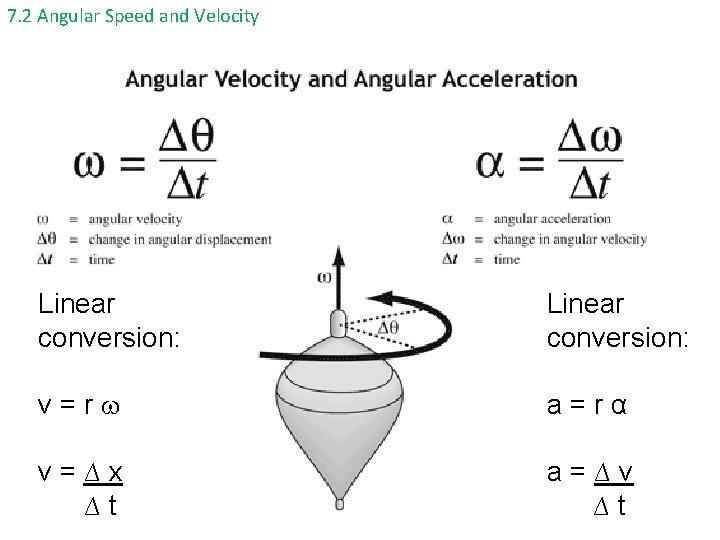
7. 2 Angular Speed and Velocity Linear conversion: v=r a=rα v=∆x ∆t a=∆v ∆t

7. 2 Angular Speed and Velocity The units of angular acceleration are rad/s 2.

Please Do Now Say these equations in English: 1. 2. 3. 4. 5. s=r v=r a=rα = / t α= / t

7. 2 Angular Speed and Velocity a) Tangential and angular speeds are related by v = rω, with ω in radians per second. Note, all of the particles rotating about a fixed axis travel in circles. All of the particles have the same angular speed (ω). Particles at different distances from the axis of rotation have different tangential speeds. b) Sparks from a grinding wheel illustrate instantaneous tangential velocity.

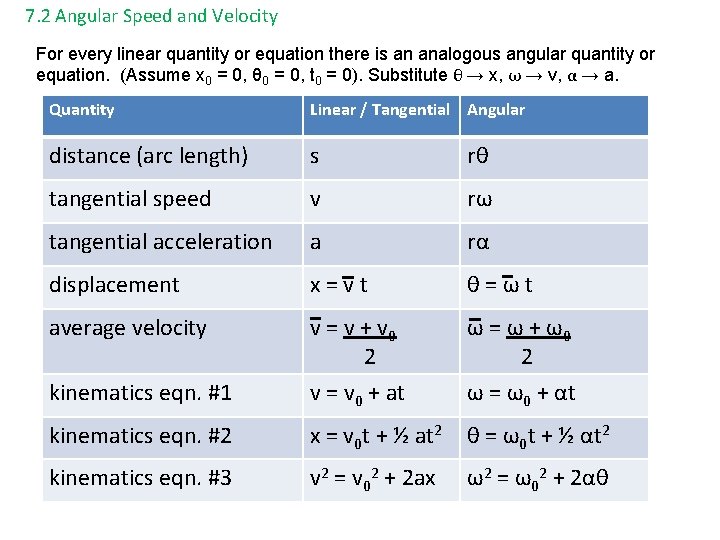
7. 2 Angular Speed and Velocity For every linear quantity or equation there is an analogous angular quantity or equation. (Assume x 0 = 0, θ 0 = 0, t 0 = 0). Substitute θ → x, ω → v, α → a. Quantity Linear / Tangential Angular distance (arc length) s rθ tangential speed v rω tangential acceleration a rα displacement x=vt θ=ωt average velocity kinematics eqn. #1 v = v + v 0 2 v = v 0 + at ω = ω + ω0 2 ω = ω0 + αt kinematics eqn. #2 x = v 0 t + ½ at 2 θ = ω0 t + ½ αt 2 kinematics eqn. #3 v 2 = v 02 + 2 ax ω2 = ω02 + 2αθ

7. 2 Angular Speed and Velocity • When angular speed and velocity are given in units of rpm (revolutions per minute) you should first convert them to rad/s before trying to solve the problem. Example 7. 2 a: Convert 33 rpm to rad/s.

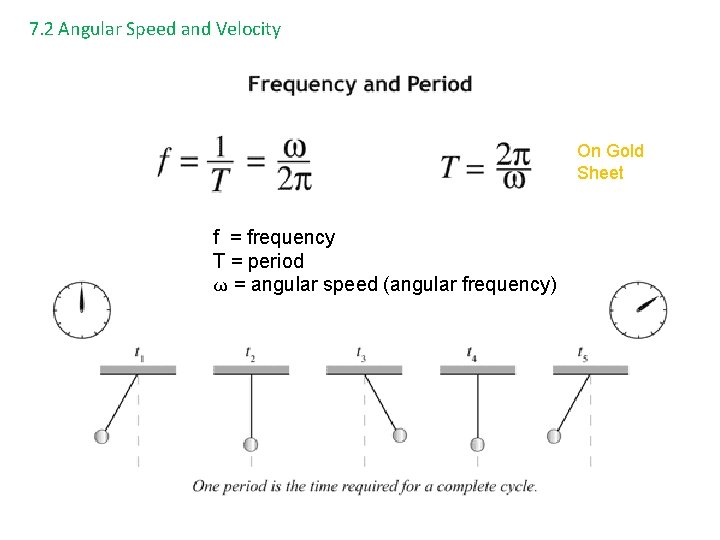
7. 2 Angular Speed and Velocity On Gold Sheet f = frequency T = period ω = angular speed (angular frequency)

7. 2 Angular Speed and Velocity (speed) • The SI unit of frequency is 1/sec or hertz (Hz).

7. 2 Angular Speed and Velocity Example 7. 2 b: A bicycle wheel rotates uniformly through 2. 0 revolutions in 4. 0 s. a) What is the average angular speed of the wheel? b) What is the tangential speed of a point 0. 10 m from the center of the wheel? c) What is the period? d) What is the frequency?

Check for Understanding

Check for Understanding

Check for Understanding

Check for Understanding

Please Do Now Answer in full sentences: 1) What is the difference between linear and angular displacement? Give an example. 2) What is the difference between angular and tangential speed? Give an example. You. Tube: Tangential velocity and acceleration www. youtube. com/watch? v=jyoeo 94 Cj. HY (17 min)

7. 4 Angular Acceleration

7. 4 Angular Acceleration • Average angular acceleration ( ) is = t • The SI unit of angular acceleration is rad/s 2. • The relationship between tangential and angular acceleration is at = r (This is not to be confused with centripetal acceleration, ac).

7. 4 Angular Acceleration speed

7. 4 Angular Acceleration

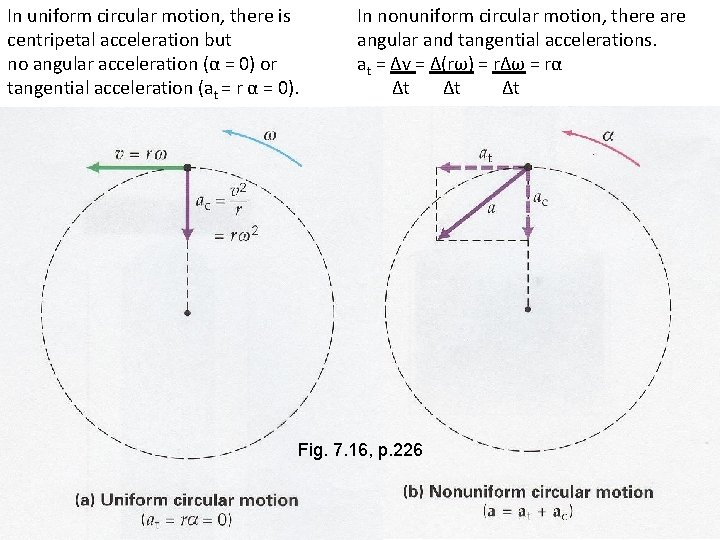
In uniform circular motion, there is centripetal acceleration but no angular acceleration (α = 0) or tangential acceleration (at = r α = 0). In nonuniform circular motion, there angular and tangential accelerations. at = ∆v = ∆(rω) = r∆ω = rα ∆t ∆t ∆t Fig. 7. 16, p. 226

7. 4 Angular Acceleration • There is always centripetal acceleration no matter whether the circular motion is uniform or nonuniform. • It is the tangential acceleration that is zero in uniform circular motion. Example 7. 4: A wheel is rotating with a constant angular acceleration of 3. 5 rad/s 2. If the initial angular velocity is 2. 0 rad/s and is speeding up, find a) the angle the wheel rotates through in 2. 0 s b) the angular speed at t = 2. 0 s

7. 4 Angular Acceleration Example 7. 5: The power on a medical centrifuge rotating at 12, 000 rpm is cut off. If the magnitude of the maximum deceleration of the centrifuge is 50 rad/s 2, how many revolutions does it rotate before coming to rest?

7. 4 Angular Acceleration Check for Understanding: 1. The angular acceleration in circular motion a. is equal in magnitude to the tangential acceleration divided by the radius b. increases the angular velocity if in the same direction c. has units of rad/s 2 d. all of the above Answer: d

7. 4 Angular Acceleration Check for Understanding: 2. Can you think of an example of a car having both centripetal acceleration and angular acceleration? Answer: Yes, when a car is changing its speed on a curve.

7. 4 Angular Acceleration Check for Understanding: 3. Is it possible for a car in circular motion to have angular acceleration but not centripetal acceleration? Answer: No, this is not possible. Any car in circular motion always has centripetal acceleration.

Homework 7. A • HW 7. A: Textbook pages 244 – 248: 8, 9, 24, 26, 27, 30, 35, 61, 63, 64.

Homework 7. A • HW 7. A: Textbook pages 244 – 248: 8, 9, 24, 26, 27, 30, 35, 61, 63, 64. Answers: 24) 3. 1 rad/s 26) 0. 087 rad/s 27) 1. 8 s 30) 0. 42 s 63) 7. 5 rev 64) 8. 40 x 10 -3 rad/s 2