AP Physics Motion in Two Dimensions Motion in

AP Physics Motion in Two Dimensions

Motion in Two Dimensions Relative Velocity Projectile Motion

Learning Objectives • Students should understand the motion of projectiles in a uniform gravitational field so they can: 1. Write down expressions for the horizontal and vertical components of velocity and position as functions of time, and sketch or identify graphs of these components.

Check for Understanding Fill in the blanks using the word bank. magnitude-angle trigonometry component kinematic tip-to-tail components 1. To analyze motion in two dimension, quantities are usually resolved into rectangular _________. 2. Once displacement, velocity, and acceleration vectors are resolved into their respective components, we can apply __________equations. 3. Vectors may be added graphically using the __________method. 4. If your vectors are at right angles, you may use the _______ method. 5. After breaking vectors down into their components, you may perform vector addition by using the analytical _________method. 6. Two ways to express the resultant vector is the ________ form and the component form.

Check for Understanding Fill in the blanks using the word bank. magnitude-angle trigonometry component kinematic tip-to-tail components 1. To analyze motion in two dimension, quantities are usually resolved into rectangular components. 2. Once displacement, velocity, and acceleration vectors are resolved into their respective components, we can apply kinematic equations. 3. Vectors may be added graphically using the tip-to-tail method. 4. If your vectors are at right angles, you may use the trigonometry method. 5. After breaking vectors down into their components, you may perform vector addition by using the analytical component method. 6. Two ways to express the resultant vector is the magnitude-angle form and the component form.

Warmup: Decipher each language equation. 1. 1 = E on C One Eye on a Cyclops 2. 1 = G. L. for M. One Giant Leap for Mankind 3. 1 = K. K on the E. S. B One King Kong on the Empire State Building 4. 1 = S. C. in D. P. One Single Calorie in Diet Pepsi 5. 1 = S. S. One Singular Sensation 6. 1 = T. that O. K One Time that Opportunity Knocks 7. 1 = W. on a U. Wheel on a Unicycle 8. 1 = if by L. One if by Land

Projectile • An object that moves through space acted upon only by the earth’s gravity.

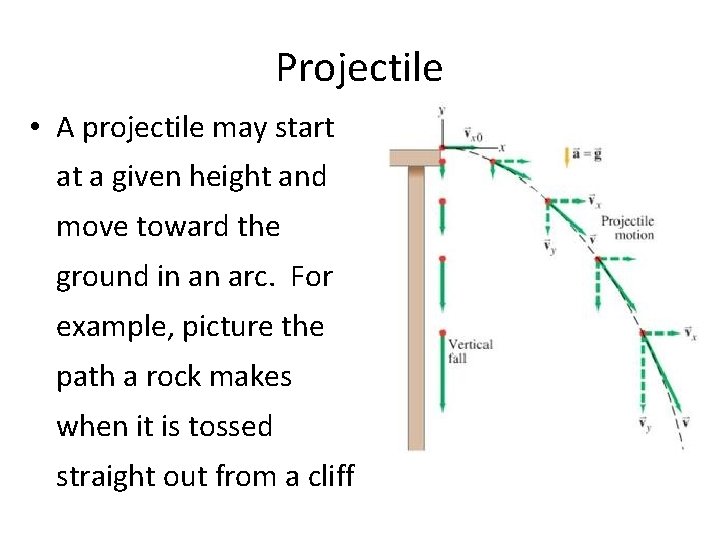
Projectile • A projectile may start at a given height and move toward the ground in an arc. For example, picture the path a rock makes when it is tossed straight out from a cliff

Projectile • A projectile may also start at a given level and the move upward and downward again as does a football that has been thrown.

Projectile Rules #1 • Projectiles always maintain a constant horizontal velocity (neglecting air resistance)

Projectile Rules #2 Projectiles always experience a constant vertical acceleration of 10 m/s 2 downward (neglecting air resistance)

Projectile Rules #3 • Horizontal and vertical motion are completely independent of each other. Therefore, the velocity of a projectile can be separated into horizontal and vertical components.

Projectile Rules #4 • For a projectile beginning and ending at the same height, the time it takes to rise to it’s highest point equals the time it takes to fall from it’s highest point back to the original position.

Projectile Rules #5 • Objects dropped from a moving vehicle have the same velocity as the moving vehicle.

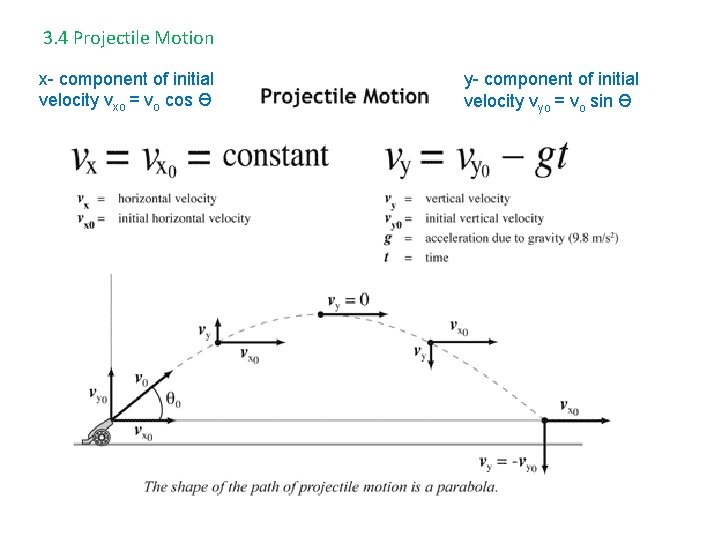
3. 4 Projectile Motion The key to projectile motion problems is recognizing the vertical and horizontal components of motion are independent. • The vertical motion, or y- component is free fall, so a = -9. 80 m/s 2 • The horizontal motion, or x- component, has zero acceleration. Why? • Time is the common factor, and can be use to link the two equations. Use kinematics equations 1 & 2 for the y- direction: vy = vyo + a t y = yo + vyo t + ½ ay t 2 Use the same equations for the x- direction: vx = vxo t

Solving Projectile Problems • To simplify calculations, the term for initial vertical velocity, vyo , will be left out of all equations in which a object is projected horizontally. For example, Δdy =vyo Δt + (1/2)gt 2 will be written as Δdy = (1/2)gt 2

3. 4 Projectile Motion x- component of initial velocity vxo = vo cos Ө y- component of initial velocity vyo = vo sin Ө

Projectile Problem # 1 • In her Physics lab, Melanie rolls a 10 g marble down a ramp and off the table with a horizontal velocity of 1. 2 m/s. The marble falls in a cup placed. 51 m from the table’s edge. How high is the table?

Projectile Problem # 1 Solution • The first thing you should note about projectile problems is that you do not need to consider the mass of the object projected. Remember, if you ignore air resistance, all bodies fall exactly the same rate regardless of their mass.

Projectile Problem # 1 • In her Physics lab, Melanie rolls a 10 g marble down a ramp and off the table with a horizontal velocity of 1. 2 m/s. The marble falls in a cup placed. 51 m from the table’s edge. How high is the table? Given: vx=1. 2 m/s dx=. 51 m Unknwn: t Equ: vx= dx / t t= dx/ vx=. 43 s

Projectile Problem # 2 • Bert is standing on a ladder picking apples in his grandfather’s orchard. As he pulls each apple off the tree, he tosses it into a basket that sits on the ground 3. 0 m below at a horizontal distance of 2 m from Bert. How fast must Bert throw the apples (horizontally) in order for them to land in the basket?

Projectile Problem # 3 Emanuel Zacchini, the famous human cannonball of Ringling Bros. And Barnum & Bailey Circus, was fired out of a cannon with a speed of 24 m/s at an angle of 40 to the horizontal. If he landed in a net 56. 6 m away at the same height from which he was fired, how long was Zacchini in the air?

Projectile Problem #4 A world record motorcycle jump occurred on August 31, 1986 when Chris Bromham took on his Yamaha and jumped a horizontal distance of 74 m across a row of cars. Assuming that he started and landed at the same level and was airborne for 1. 3 s, what height from his starting point did this daredevil achieve?

Projectile Problem #5 A package is dropped from an airplane travelling with a constant horizontal speed of 120 m/s at an altitude of 500 m. What is the horizontal distance the package travels before hitting the ground (range)?

Example: A package is dropped from an airplane travelling with a constant horizontal speed of 120 m/s at an altitude of 500 m. What is the horizontal distance the package travels before hitting the ground (range)? Solution: Given: horizontal motion vxo = 120 m/s vertical motion vyo = 0 y = -500 m y vo = vxo x 500 m Find: range Since the range is given by x = vxo t , we have to find the time of flight t first. From the vertical motion, we use y = vyot + ½ ayt 2 So, -500 m = 0 + ½ (-9. 80 m/s 2) t 2, solving, t = 10. 1 s Therefore, x = (120 m/s)(10. 1 s) = 1. 21 x 103 m = 1. 21 km Hint: The quantities such as initial velocities and displacements have to be treated independently. For example, the initial horizontal velocity is 120 m/s and the initial vertical velocity is zero. The 12. 0 m/s can only be used in the horizontal motion and the 0 m/s can only be used in the vertical motion. A common mistake is to mix up these quantities or not treat them as independent.

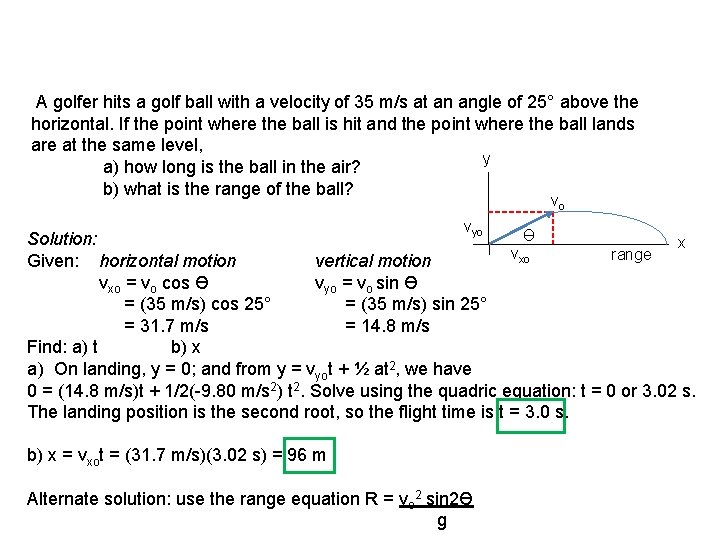
Projectile Problem #6 A golfer hits a golf ball with a velocity of 35 m/s at an angle of 25° above the horizontal. If the point where the ball is hit and the point where the ball lands are at the same level, a) how long is the ball in the air? b) what is the range of the ball?

A golfer hits a golf ball with a velocity of 35 m/s at an angle of 25° above the horizontal. If the point where the ball is hit and the point where the ball lands are at the same level, y a) how long is the ball in the air? b) what is the range of the ball? vo vyo Ө Solution: x v range xo Given: horizontal motion vertical motion vxo = vo cos Ө vyo = vo sin Ө = (35 m/s) cos 25° = (35 m/s) sin 25° = 31. 7 m/s = 14. 8 m/s Find: a) t b) x a) On landing, y = 0; and from y = vyot + ½ at 2, we have 0 = (14. 8 m/s)t + 1/2(-9. 80 m/s 2) t 2. Solve using the quadric equation: t = 0 or 3. 02 s. The landing position is the second root, so the flight time is t = 3. 0 s. b) x = vxot = (31. 7 m/s)(3. 02 s) = 96 m Alternate solution: use the range equation R = vo 2 sin 2Ө g

Check for Understanding:

vy = vyo + at ; vy = 0 at peak. x = vxo t