AP Physics Chapter 7 Energy of a System




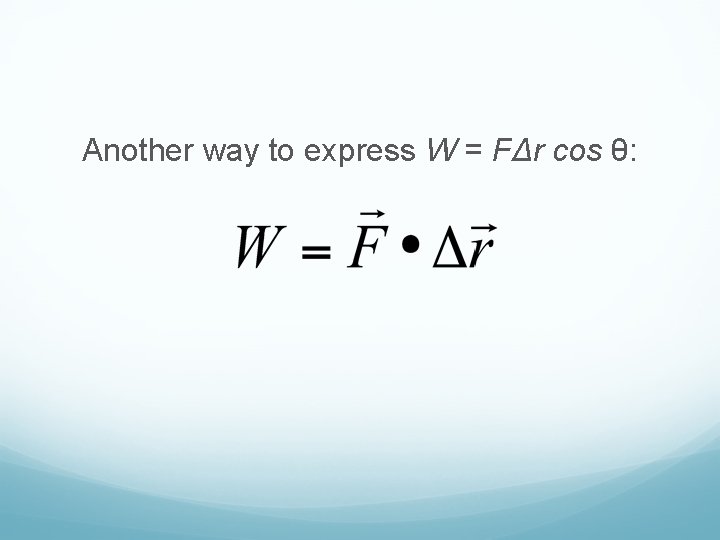




































- Slides: 51

AP Physics: Chapter 7 Energy of a System

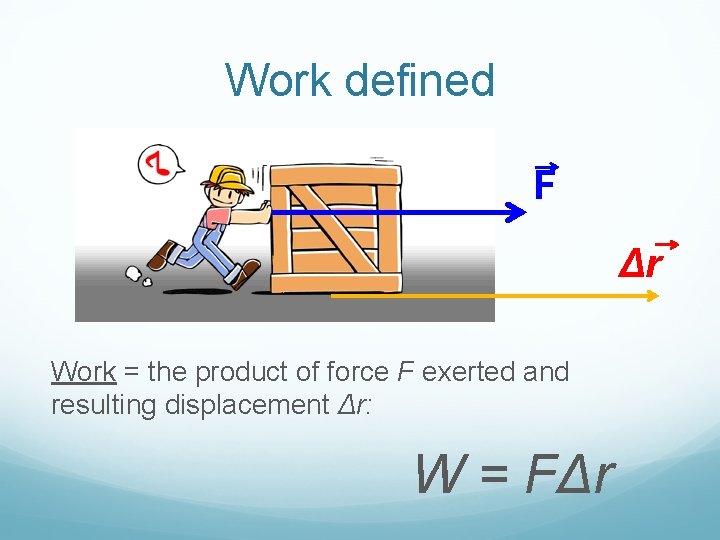
Work defined F Δr Work = the product of force F exerted and resulting displacement Δr: W = FΔr

Units: W = FΔr Joules (J) meters (m) Newtons (N)

Remember… If you work hard… …you can make a lot of money… … and buy a lot of jewels joules!

Displacement is sometimes indicated by the symbol d, so, W = Fd Recall Newton’s 2 nd law: F = ma. If you substitute Newton’s 2 nd Law into the formula for work you get: W = mad A simple, yet elegant proof that work makes you mad!

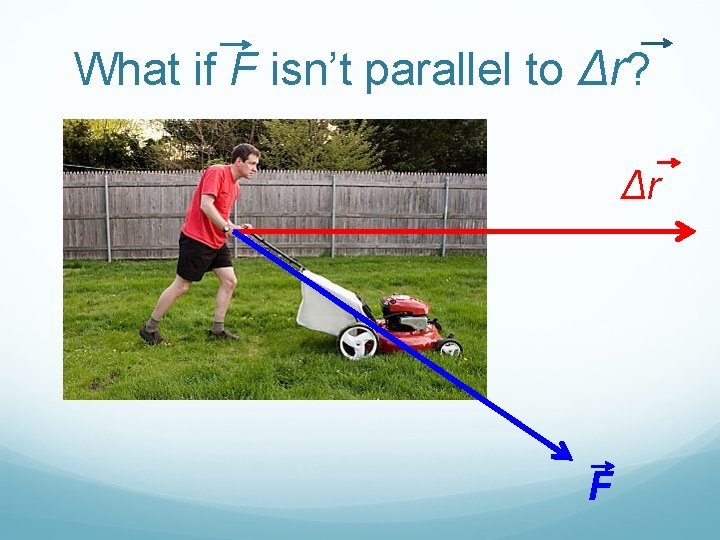
What if F isn’t parallel to Δr? Δr F

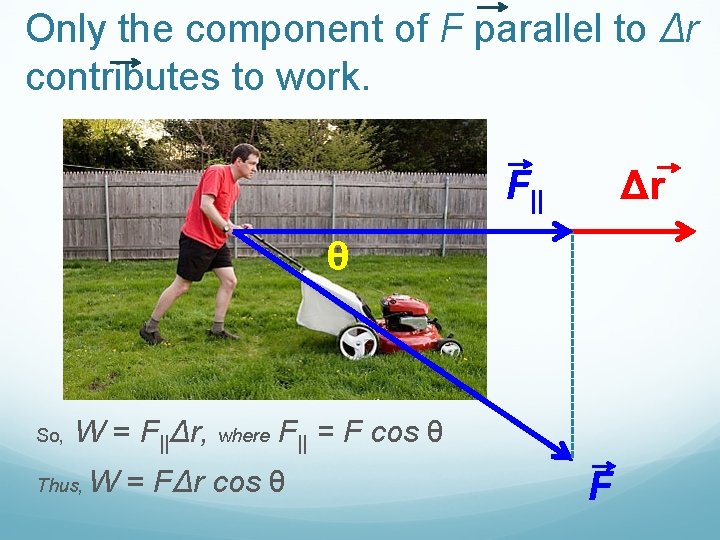
Only the component of F parallel to Δr contributes to work. F|| Δr θ So, W = F||Δr, where F|| = F cos θ Thus, W = FΔr cos θ F
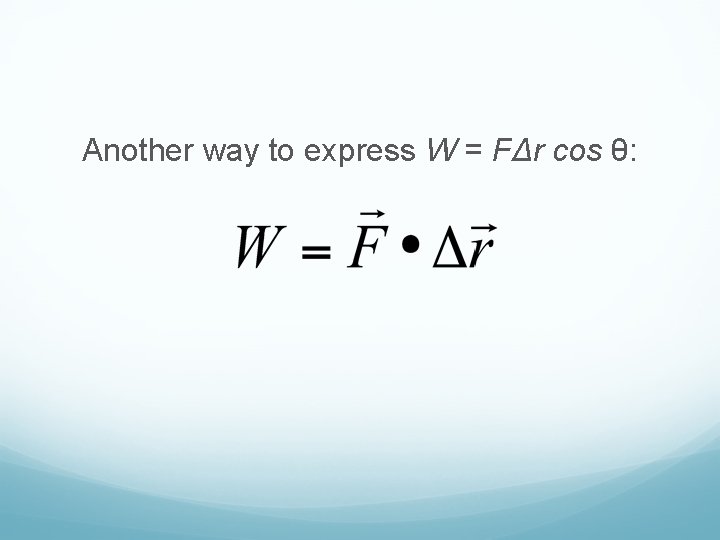
Another way to express W = FΔr cos θ:

A Mathemagical Interlude: Dot Products Consider the following two vectors: The dot product (also known as “scalar product”) is defined as: And the dot product may be calculated:

Ex) Find the angle between the following two vectors:

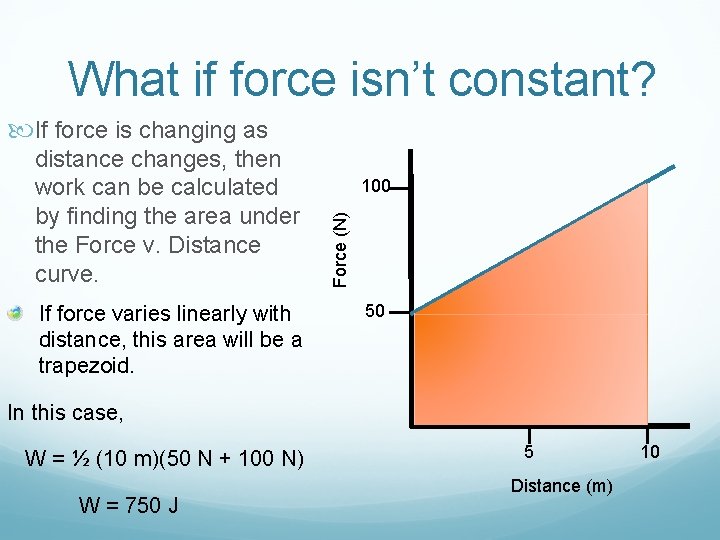
What if force isn’t constant? If force is changing as If force varies linearly with distance, this area will be a trapezoid. 100 Force (N) distance changes, then work can be calculated by finding the area under the Force v. Distance curve. 50 In this case, W = ½ (10 m)(50 N + 100 N) W = 750 J 5 Distance (m) 10

What if force v. displacement is a nonlinear curve? In general:

Example: Work Done by a Spring Force Spring force = force due to the stretching or compressing of a spring away from an equilibrium position.

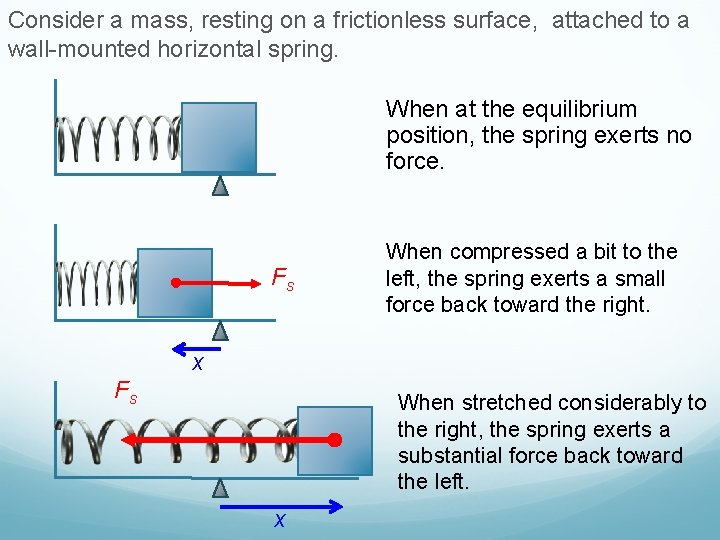
Consider a mass, resting on a frictionless surface, attached to a wall-mounted horizontal spring. When at the equilibrium position, the spring exerts no force. Fs When compressed a bit to the left, the spring exerts a small force back toward the right. x Fs When stretched considerably to the right, the spring exerts a substantial force back toward the left. x

Hooke’s Law Note: Spring force is always proportional to displacement, but in the opposite direction. So, Fs ~ –x Insert a constant of proportionality: Fs = –kx This equation is known as “Hooke’s Law” k = “spring constant” and is a measure of how rigid the spring is.

Calculating Work Done by a Spring Apply Hooke’s Law to find work done by a spring moving a mass from xi to xf:

Work Done by the Spring v. Work Done by Person In the previous slide we calculated the work done by the spring. If you consider the work done by an external force, such as a person stretching the spring, now the force and displacement vectors point in the same direction. So now, F = kx, not –kx:

Work & Machines No device can perform more joules of work in order to accomplish a task than the number of joules of work that are input into the machine by the user. (In other words, machines cannot create energy. ) A simple machine, however, is a device that can alter the magnitude or direction of the force it takes to accomplish a task. Since W = Fd, if a machine lessens the amount of force F necessary to accomplish a task, and W must remain the same (or even greater – but we’ll get to that in a moment!), the price you pay for using the machine is having to exert your force over a longer distance d.

Example of a Simple Machine: The Inclined Plane Suppose you want to lift a 1000 -N refrigerator into the back of a moving truck 0. 75 m off the ground. Without the ramp, you’d Fout dout have to actually exert 1000 N of force straight up over a distance of 0. 75 m. These values can be considered the output force and output distance of the machine, respectively.

Example of a Simple Machine: The Inclined Plane The ramp, however, lets the user apply a force much smaller than the actual weight of the fridge. Fin Fout The price the user din dout pays is having to exert that smaller force over a longer distance, in this case the length of the ramp.

In an ideal machine, Wout = Win If the ramp is 3. 0 m long, how much effort force should the user need to input? Fin Fout Assuming ideal conditions, Foutdout = Findin N)(0. 75 m) = F din dout (1000 m) in(3 So, Fin = 250 N

Realistically, no machine is ideal Instead of ideal conditions, suppose the user has to overcome 50 N of friction on the ramp Fin Fout In this case, the actual din dout input force would be Fin = 250 + 50 = 300 N.

Work in v. Work out Win = Findin = (300 N)(3 m) = 900 J Wout = Foutdout = (1000 N)(0. 75 m) = 750 J Fin Fout Efficiency is defined as the ratio of useful output work to amount of input work: η = Wout/Win dout In this case, η = 750 J/900 J = 0. 83, or 83%

Work in v. Work out 83% of the energy exerted by the user translated into actual useful work done; the other 17% was used overcoming friction. So 900 J of work was input in order to accomplish a 750 J task Fin Fout Was it worth it? din dout Probably, unless you want a back injury! 300 N of effort force is still way less than 1000 N!

Mechanical Advantage The ratio of output force to input force is called mechanical advantage: MA = Fout/Fin In this case, MA = 1000 N / 300 N Fin Fout = 3. 3 So this machine can din dout be thought to amplify a user’s strength by a factor 3. 3

Ideal Mechanical Advantage Recall, when we assumed this machine was ideal, we computed 250 N as our estimate for input force. We did this using the known input and output distances. Fin Fout Ideal Mechanical Advantage is defined as the ratio of the input to output distances: IMA = din/dout din dout In this case, IMA = 3 m/0. 75 m = 4

Another example of a simple machine: The Lever Give me a lever long enough and a place to stand, and I shall move the Earth. - Archimedes

More Simple Machines Screw Pulley Wheel & Axle Wedge

Compound Machines A compound machine is composed of 2 or more simple machines connected in such a way that the output force of one simple machine becomes the input force of the next component. Note: ηtotal = η 1η 2η 3… MAtotal = MA 1 MA 2 MA 3… IMAtotal = IMA 1 IMA 2 IMA 3…

Work & Energy is defined as the capacity to do work. Conversely, if work is done on an object, that object has gained energy: W = ΔE Like work, energy is measured in Joules

Types of Energy Mechanical Energy Kinetic Energy (K) – energy due to motion Potential Energy (U) – energy due to location Gravitational Potential Energy – energy due to height Spring Potential Energy – energy due to being on a stretched or compressed spring Thermal Energy (Q) – energy due to heat (i. e. movement of particles making up the body) Other forms of energy include radiant energy (i. e. light), chemical energy (Duracells and donuts), nuclear energy, and “rest energy” (i. e. mass).

Kinetic Energy If work is done accelerating an object, that object has gained kinetic energy – the energy of motion. Recall: vf 2 = vi 2 + 2 aΔx Here, W = ΔE, i. e. W = Kf – Ki But F = ma, so a = F/m Since FΔx = W, Kf must = ½mvf 2 and Ki must = ½mvi 2 Thus, vf 2 = vi 2 + 2(F/m)Δx vf 2 - vi 2 = 2(F/m)Δx FΔx = ½mvf 2 -½mvi 2 So the general formula for kinetic energy is K = ½mv 2

Alternate Derivation of Kinetic Energy Equation: If work is done accelerating an object, then F = ma, so Note: dx/dx cancels; dx/dt = v

So once again we obtain the formula for kinetic energy: K = ½mv 2 Work-Kinetic Energy Theorem: If work is done to accelerate an object, W = ΔK

Skidding distance Car A and Car B are identical except Car B is going twice as fast as Car A. Both cars slam on the brakes at the same time. How far will Car B skid compared to Car A? a. ) The same distance b. ) Twice as far c. ) Four times as far

Skidding distance Car A and Car B are identical except Car B is going twice as fast as Car A. Both cars slam on the brakes at the same time. How far will Car B skid compared to Car A? a. ) The same distance b. ) Twice as far c. ) Four times as far

Skidding distance EK = ½ mv 2, so if Car B has twice the speed as Car A, it has 4 x the kinetic energy. Therefore, 4 times as much work must be done stopping it. W = Fd Since both cars are identical, both experience the same amount of braking force, so Car B must experience that force for 4 times the distance!

Gravitational Potential Energy If work is done lifting an object of mass m up a height y, that object has gained gravitational potential energy Recall W = Fd. In this case, d = y. The force required to lift mass m is mg. So the formula for gravitational PE is: Ugrav = mgy

U is relative Suppose a 1. 0 -kg book is on top of a 1. 0 -m tall desk on the roof of a 100. 0 -m tall building on top of a 200. 0 -m tall hill in a city 500. 0 m above sea level which is 6, 378, 000 m from the center of the Earth. What is the potential energy of the book? Answer: Relative to what? Now suppose we move the book from the 1. 0 -m tall desk to a 1. 5 -m tall shelf. What is the book’s change in potential energy? Regardless of where our line of reference is, the book has moved 0. 5 m, so ΔU = mgΔy = (1. 0 kg)(9. 8 m/s 2)(0. 5 m) = 4. 9 J The moral of the story: U is relative; ΔU is not.

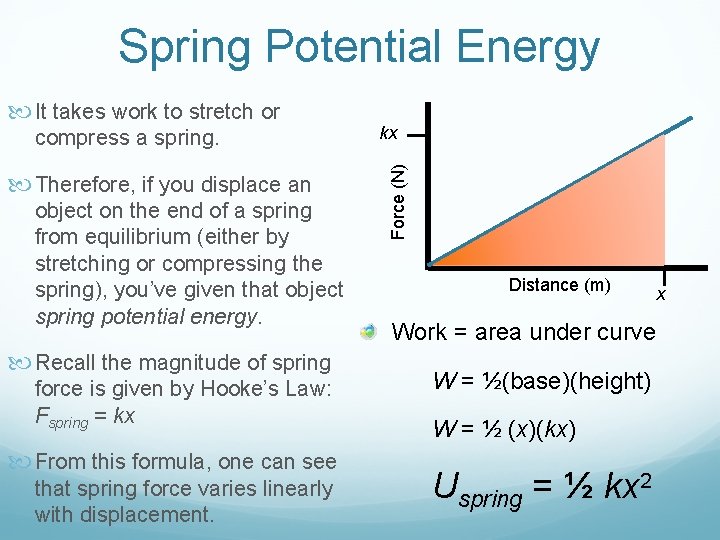
Spring Potential Energy compress a spring. Therefore, if you displace an object on the end of a spring from equilibrium (either by stretching or compressing the spring), you’ve given that object spring potential energy. Recall the magnitude of spring force is given by Hooke’s Law: Fspring = kx From this formula, one can see that spring force varies linearly with displacement. kx Force (N) It takes work to stretch or Distance (m) Work = area under curve W = ½(base)(height) W = ½ (x)(kx) Uspring = ½ kx 2 x

“Conservative” Forces may be classified as “conservative” or “nonconservative” Conservative Forces have these two equivalent properties: The work done by a conservative force on a particle moving between any two points is independent of the path taken The work done by a conservative force on particle moving through a closed path is zero. So what’s conserved by a “conservative” force? The answer is: Mechanical Energy Recall: Emech = K + U

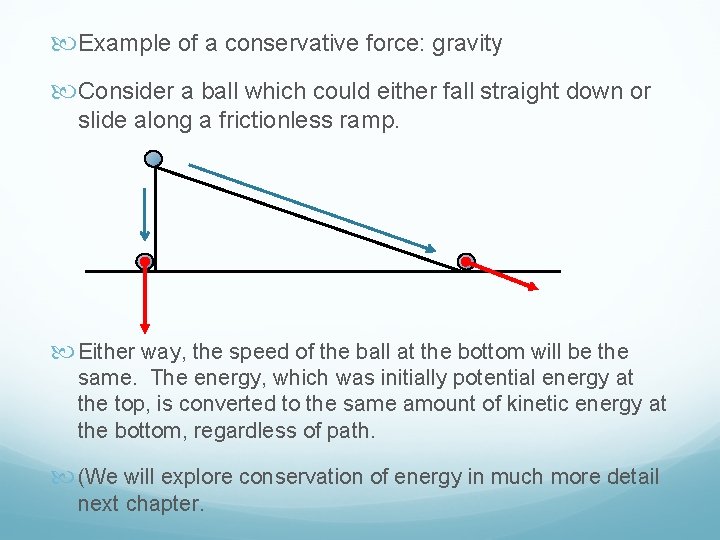
Example of a conservative force: gravity Consider a ball which could either fall straight down or slide along a frictionless ramp. Either way, the speed of the ball at the bottom will be the same. The energy, which was initially potential energy at the top, is converted to the same amount of kinetic energy at the bottom, regardless of path. (We will explore conservation of energy in much more detail next chapter.

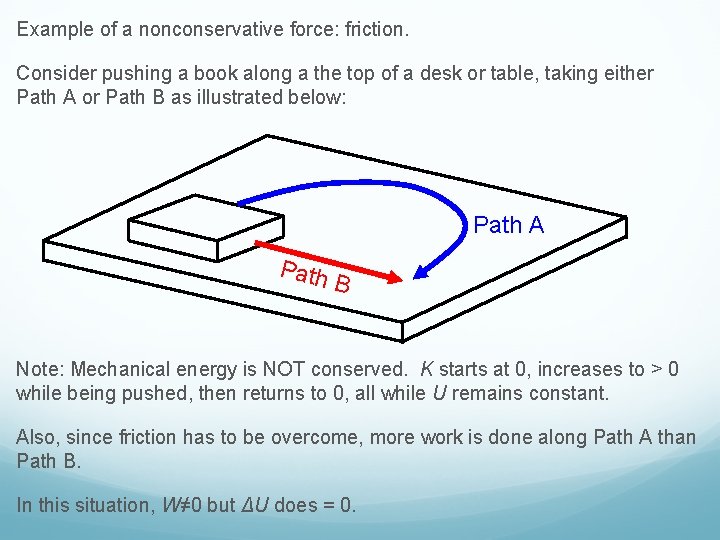
Example of a nonconservative force: friction. Consider pushing a book along a the top of a desk or table, taking either Path A or Path B as illustrated below: Path A Path B Note: Mechanical energy is NOT conserved. K starts at 0, increases to > 0 while being pushed, then returns to 0, all while U remains constant. Also, since friction has to be overcome, more work is done along Path A than Path B. In this situation, W≠ 0 but ΔU does = 0.

So if a force is conservative, we can say: W = –ΔU That is to say, work done = loss in potential energy. Recall: So for a conservative force, Conversely,

That is easily confirmed with springs:

Energy & Stability Recall: An object is in equilibrium if Fnet = 0. An object is in stable equilibrium if any movement results in a force directing the object back to where it was. Example: A marble in a bowl An object is in unstable equilibrium if any movement results in a force directing the object to continue accelerating away. Example: A marble on a hill An object is in neutral equilibrium if any movement results in neither a force back nor force away. Example: A marble on a tabletop

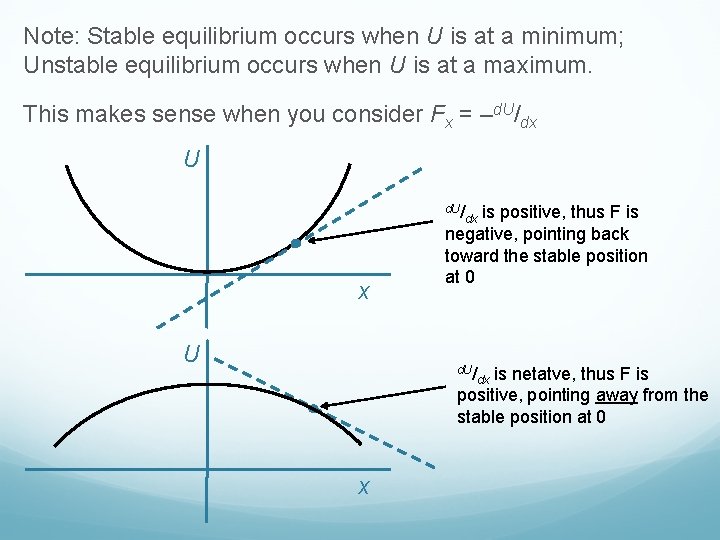
Note: Stable equilibrium occurs when U is at a minimum; Unstable equilibrium occurs when U is at a maximum. This makes sense when you consider Fx = –d. U/dx U d. U/ x U is positive, thus F is negative, pointing back toward the stable position at 0 dx d. U/ is netatve, thus F is positive, pointing away from the stable position at 0 x dx

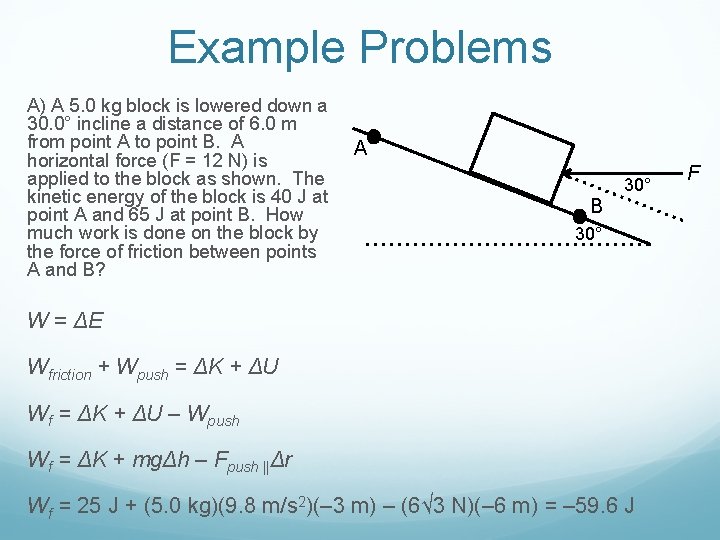
Example Problems A) A 5. 0 kg block is lowered down a 30. 0° incline a distance of 6. 0 m from point A to point B. A horizontal force (F = 12 N) is applied to the block as shown. The kinetic energy of the block is 40 J at point A and 65 J at point B. How much work is done on the block by the force of friction between points A and B? A 30° B 30° W = ΔE Wfriction + Wpush = ΔK + ΔU Wf = ΔK + ΔU – Wpush Wf = ΔK + mgΔh – Fpush ||Δr Wf = 25 J + (5. 0 kg)(9. 8 m/s 2)(– 3 m) – (6√ 3 N)(– 6 m) = – 59. 6 J F

B) As a 6. 0 -kg object moves from (4 i – 7 j)m to (12 i + 3 j)m, the constant force acting on it is (5 i + 6 j)N. If the initial speed of the object is 8 m/s, what is its kinetic energy at its final position?

C) For the potential U = x 3 – 12 x 2 + 36 x + 42, find the points of equilibrium and label stable or unstable. Stable equilibrium occurs if U is a minimum; Unstable equilibrium occurs if U is a maximum. d. U/ dx = 0 for x = 2, 6

C) For the potential U = x 3 – 12 x 2 + 36 x + 42, find the points of equilibrium and label stable or unstable. Stable equilibrium occurs if U is a minimum; Unstable equilibrium occurs if U is a maximum. Concave down Maximum Concave up Minimum Stable equilibrium @ x = 6; unstable equilibrium @ x = 2