AP Physics Chapter 3 Motion in Two Dimensions

AP Physics Chapter 3 Motion in Two Dimensions

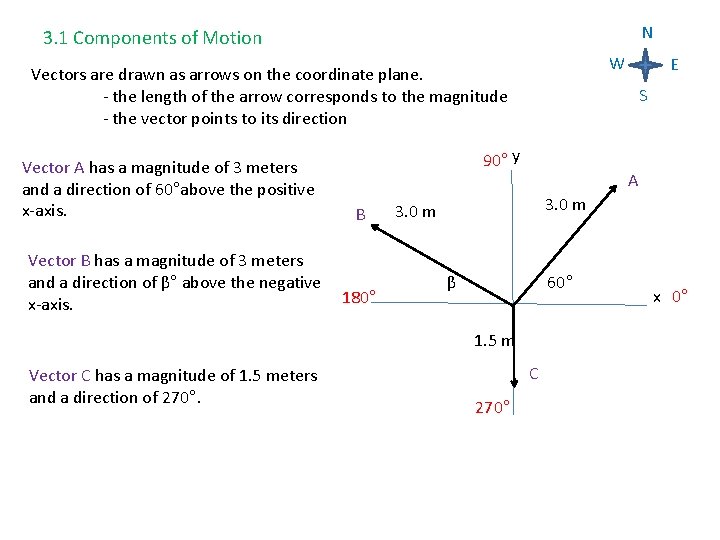
N 3. 1 Components of Motion W Vectors are drawn as arrows on the coordinate plane. - the length of the arrow corresponds to the magnitude - the vector points to its direction Vector A has a magnitude of 3 meters and a direction of 60°above the positive x-axis. S 90° y B Vector B has a magnitude of 3 meters and a direction of β° above the negative 180° x-axis. A 3. 0 m 60° β 1. 5 m Vector C has a magnitude of 1. 5 meters and a direction of 270°. E C 270° x 0°

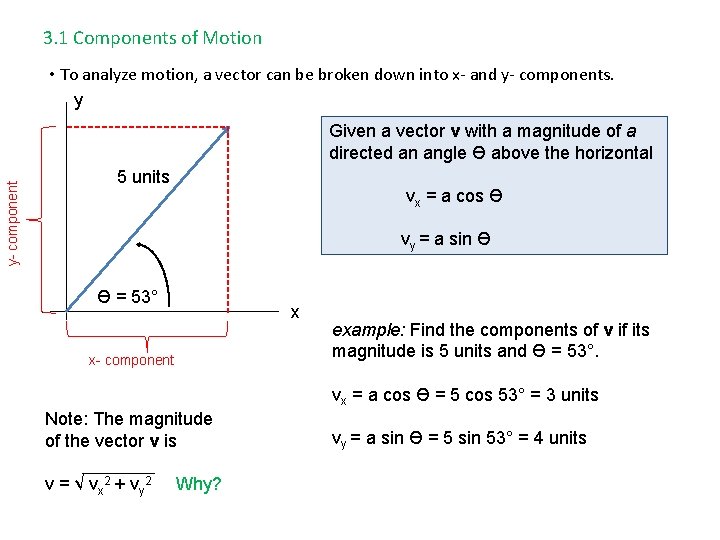
3. 1 Components of Motion • To analyze motion, a vector can be broken down into x- and y- components. y y- component Given a vector v with a magnitude of a directed an angle Ө above the horizontal 5 units vx = a cos Ө vy = a sin Ө Ө = 53° x x- component example: Find the components of v if its magnitude is 5 units and Ө = 53°. vx = a cos Ө = 5 cos 53° = 3 units Note: The magnitude of the vector v is v = √ v x 2 + vy 2 Why? vy = a sin Ө = 5 sin 53° = 4 units

3. 1 Components of Motion • Kinematics problems in two-dimensions can be solved by: • resolving the displacement, velocity, and acceleration vectors into their respective components. • using the three constant acceleration equations separately for the x and y directions. • using the Pythagorean theorem to find the magnitude of your resultant vector. • using an inverse trig function to find the angle of your resultant vector

3. 1 Components of Motion Example 1: A boat travels with a speed of 5. 0 m/s in a straight path on a still lake. Suddenly, a steady wind pushes the boat perpendicularly to its straight line path with a speed of 3. 0 m/s for 5. 0 s. Relative to its position just when the wind started to blow, where is the boat at the end of this time? Solution: List givens for x and y directions separately. x-direction vo = 5. 0 m/s a=0 y-direction vo = 3. 0 m/s a=0 Unknowns: x and y Common to both: t = 5. 0 s Analysis: Both motions are motion with constant velocity. Choose the straight path of the boat as the x axis and the direction of the wind as the y axis. Sketch: wind y boat d Ө x

x-direction vo = 5. 0 m/s a=0 y-direction vo = 3. 0 m/s a=0 Unknowns: x and y wind y d Common to both: t = 5. 0 s boat Ө x-component: (use equation 1) x = vot + ½ at 2 = (5. 0 m/s)(5. 0 s) + 0 = 25 m y-component: (use equation 1) y = vot + ½ at 2 = (3. 0 m/s)(5. 0 s) + 0 = 15 m Now, d = √ x 2 + y 2 = √ (25 m)2 + (15 m)2 = 29 m And Ө = tan-1 y = 15 m = 31° 25 m x

3. 2 Vector Addition and Subtraction vector addition – combining vector quantities by using one of several techniques • geometric methods (triangle, parallelogram, polygon) • vector components and the analytical component method vector subtraction – a special case of vector addition • A - B = A + (-B) • subtracting a vector is the same as adding a negative vector resultant – the overall effect of combining vectors; the vector sum Example: Add vectors A + B + C = R Solution: Use tip-to-tail method

3. 2 Vector Addition and Subtraction • Geometric (Graphical) Methods • use a convenient scale (ex: 1 cm = 10 meters) • To add vectors A and B, draw them tip-to-tail, starting at the origin. • The vector that extends from the tail of A to the tip of B, completing the triangle, is the resultant R = A + B. • When drawn to scale, the magnitude of R can be found by measuring R and using the scale conversion. • Use a protractor to measure the direction of the resultant, ӨR. • You may add on as many vectors as you like; the order doesn’t matter! Example: Add three vectors graphically. Solution:

3. 2 Vector Addition and Subtraction • Analytical (Trigonometry) Method • When vectors make a right triangle with each other, • use the Pythagorean theorem to find the magnitude of your resultant vector. • use the inverse trig function to find the angle of your resultant vector. H Ө A O A = side adjacent to angle Ө O = side opposite to angle Ө H = hypotenuse of triangle SOH – CAH - TOA sin Ө = O A cos Ө = A H tan Ө = O A Ө = sin-1 O A Ө = cos-1 A H Ө = tan-1 O A

3. 2 Vector Addition and Subtraction Example: Eric leaves the base camp and hikes 11 km, north and then hikes 11 km east. Determine Eric's resulting displacement and express in the magnitude-angle form. Solution: Magnitude of displacement = 16 km

3. 2 Vector Addition and Subtraction

3. 2 Vector Addition and Subtraction

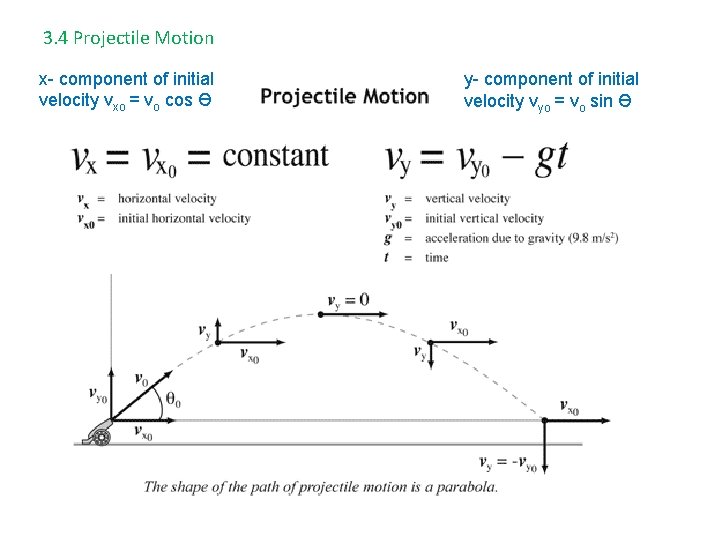
3. 4 Projectile Motion projectile – an object upon which the only force is gravity. The key to projectile motion problems is recognizing the vertical and horizontal components of motion are independent. • The vertical motion, or y- component is free fall, so a = -9. 80 m/s 2 • The horizontal motion, or x- component, has zero acceleration. Why? • Time is the common factor, and can be use to link the two equations. Use kinematics equations 1 & 2 for the y- direction: vy = vyo + a t y = yo + vyo t + ½ ay t 2 Use the same equations for the x- direction: vx = vxo t

3. 4 Projectile Motion x- component of initial velocity vxo = vo cos Ө y- component of initial velocity vyo = vo sin Ө

Example: A package is dropped from an airplane travelling with a constant horizontal speed of 120 m/s at an altitude of 500 m. What is the horizontal distance the package travels before hitting the ground (range)? Solution: Given: horizontal motion vxo = 120 m/s vertical motion vyo = 0 y = -500 m y vo = vxo x 500 m Find: range Since the range is given by x = vxo t , we have to find the time of flight t first. From the vertical motion, we use y = vyot + ½ ayt 2 So, -500 m = 0 + ½ (-9. 80 m/s 2) t 2, solving, t = 10. 1 s Therefore, x = (120 m/s)(10. 1 s) = 1. 21 x 103 m = 1. 21 km Hint: The quantities such as initial velocities and displacements have to be treated independently. For example, the initial horizontal velocity is 120 m/s and the initial vertical velocity is zero. The 12. 0 m/s can only be used in the horizontal motion and the 0 m/s can only be used in the vertical motion. A common mistake is to mix up these quantities or not treat them as independent.

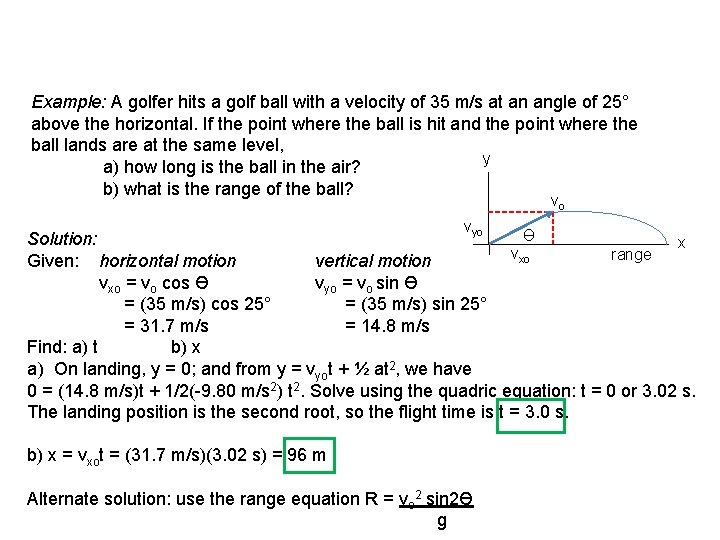
Example: A golfer hits a golf ball with a velocity of 35 m/s at an angle of 25° above the horizontal. If the point where the ball is hit and the point where the ball lands are at the same level, y a) how long is the ball in the air? b) what is the range of the ball? vo vyo Ө Solution: x v range xo Given: horizontal motion vertical motion vxo = vo cos Ө vyo = vo sin Ө = (35 m/s) cos 25° = (35 m/s) sin 25° = 31. 7 m/s = 14. 8 m/s Find: a) t b) x a) On landing, y = 0; and from y = vyot + ½ at 2, we have 0 = (14. 8 m/s)t + 1/2(-9. 80 m/s 2) t 2. Solve using the quadric equation: t = 0 or 3. 02 s. The landing position is the second root, so the flight time is t = 3. 0 s. b) x = vxot = (31. 7 m/s)(3. 02 s) = 96 m Alternate solution: use the range equation R = vo 2 sin 2Ө g

Check for Understanding:

vy = vyo + at ; vy = 0 at peak. x = vxo t