AP PHYSICS 1 Sound Loudness Intensity and Doppler

AP PHYSICS 1 Sound Loudness Intensity and Doppler

Sound Waves • Sound is longitudinal pressure (compression) waves • Range of hearing: 20 Hz to 20, 000 Hz FREQUENCY DEMO

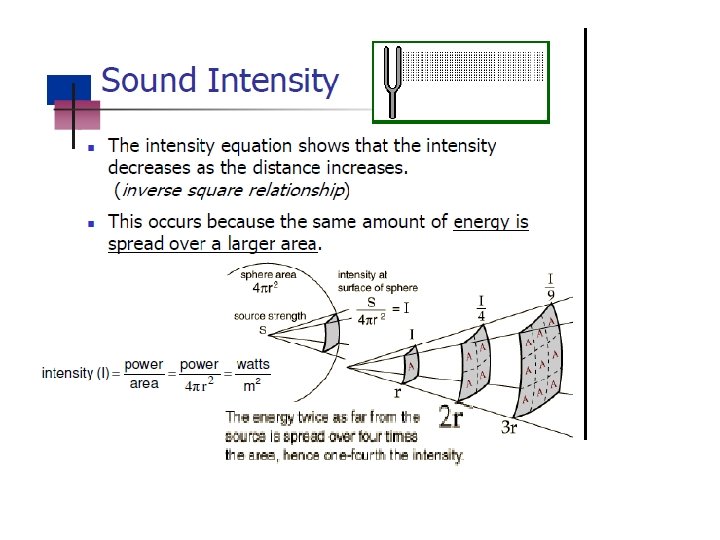
Intensity of Sound Waves Power Area SI units are W/m 2 Intensity is proportional to square of amplitude (pressure modulation)

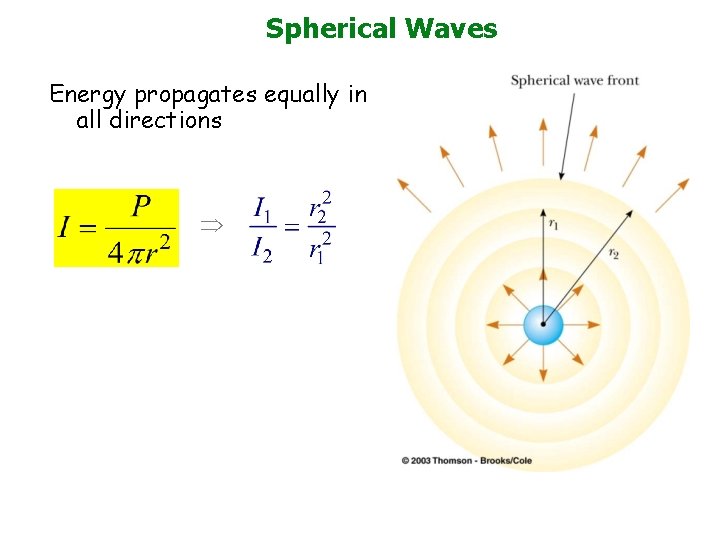
Spherical Waves Energy propagates equally in all directions Þ

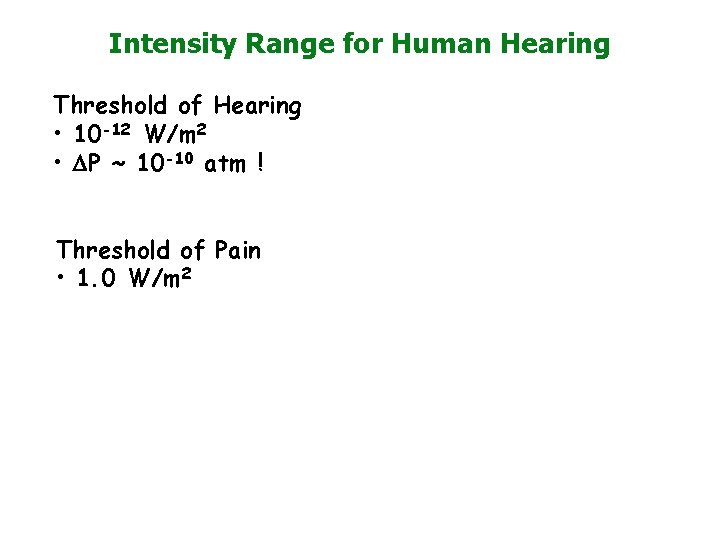
Intensity Range for Human Hearing Threshold of Hearing • 10 -12 W/m 2 • DP ~ 10 -10 atm ! Threshold of Pain • 1. 0 W/m 2

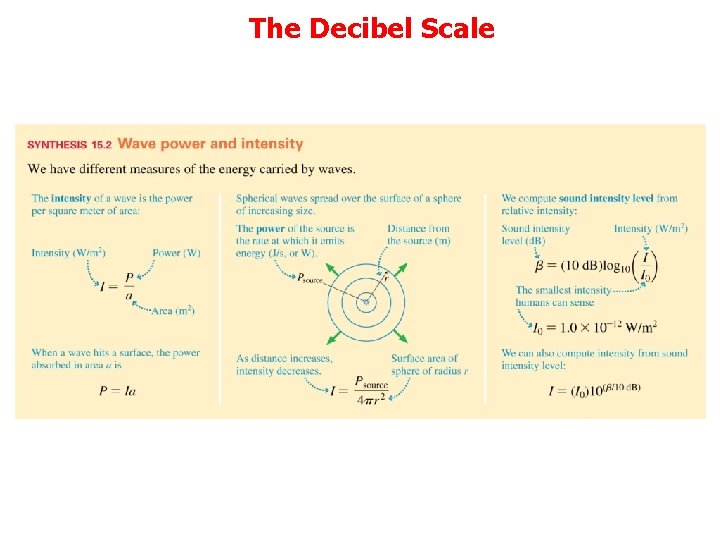
Decibel Scale Sensation is logarithmic • I 0 is threshold of hearing (0 d. B) • Threshold of Pain is therefore 120 d. B

Intensity vs. Intensity Level • INTENSITY is P/A, W/m 2 • INTENSITY LEVEL is in decibels (dimensionless)

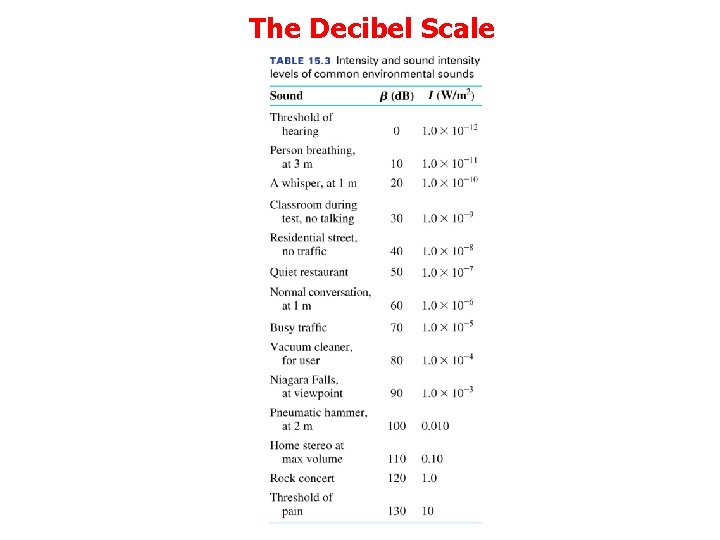
The Decibel Scale • The threshold of hearing is the lowest intensity sound that can be heard. It is where we place the 0 for our loudness scale. For the average human, it is I 0 = 1. 0 10 12 W/m 2 • The sound intensity level is expressed in decibels (d. B) as

The Decibel Scale • As a reminder, logarithms work like this:

The Decibel Scale • Right at the threshold of hearing, where I = I 0, the sound intensity level is • The threshold of hearing corresponds to 0 d. B. © 2015 Pearson Education, Inc. Slide 15 -13

Sound Level Demo Sound d. B Demo

Example 14. 2 A noisy machine in a factory produces a sound with a level of 80 d. B. How many machines can the factory house without exceeding the 100 -d. B limit? a) 12. 5 machines b) 20 machines c) 100 machines

The Decibel Scale • We can find the intensity from the sound intensity level by taking the inverse of the log 10 function • Recall, from the definition of the base-10 logarithm, that 10 log(x) = x. • Applying this to Equation 15. 14, we find I = (I 0)10(β/10 d. B)

The Decibel Scale

Example 14. 3 (skip) A train sounds its horn as it approaches an intersection. The horn can just be heard at a level of 50 d. B by an observer 10 km away. Treating the horn as a point source and neglect any absorption of sound by the air or ground, a) What is the average power generated by the horn? a) 126 W b) What intensity level of the horn’s sound is observed by someone waiting at an intersection 50 m from the train? b) 96 d. B

Example 14. 4 Bozo Bob buys a 20 -W train whistle and figures out that he won’t have any trouble standing 2 meters from the whistle since his stereo speakers are rated at 100 W and he has little trouble with the speakers turned all the way up. What is the intensity level of the whistle? 116 d. B

Finding the loudness of a shout A person shouting at the top of his lungs emits about 1. 0 W of energy as sound waves. What is the sound intensity level 1. 0 m from such a person? PREPARE We will assume that the shouting person emits a spherical sound wave.

Example 15. 11 Finding the loudness of a shout SOLVE At a distance of 1. 0 m, the sound intensity is Thus the sound intensity level is ASSESS This is quite loud as you might expect.

Example Problem You are working in a shop where the noise level is a constant 90 d. B. A. Your eardrum has a diameter of approximately 8. 4 mm. How much power is being received by one of your eardrums? B. This level of noise is damaging over a long time, so you use earplugs that are rated to reduce the sound intensity level by 26 d. B, a typical rating. What is the power received by one eardrum now? Answer: part A: the power = intensity*area (eq. 15. 11). The intensity is 1 e-12*10^9 for 90 d. B noise level (eq. 15) or 1 E-3 w/M^2, so the power is 1 E-3*pi*(8. 4 e-3)^2 = 2. 2 E-7 W part B: The power is now reduced by a factor of 10^(2. 6), so the new power is 5. 6 E-10 W.

The Decibel Scale

Doppler Effect A change in the frequency experienced by an observer due to motion of either the observer or the source. DOPPLER DEMO

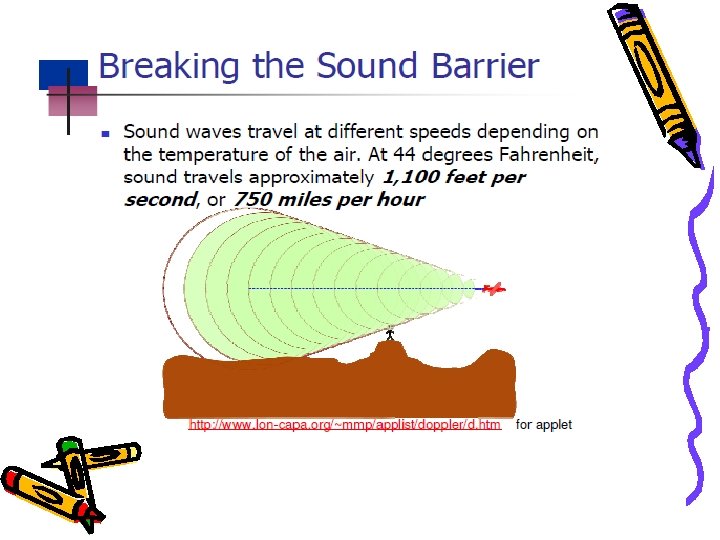
The Doppler Effect and Shock Waves • The Doppler effect is a change in frequency due to the motion of the source. This effect is heard as the pitch of an ambulance siren changes from its approach to after it has passed you by. • A shock wave is produced when an object moves faster than the speed of sound. • When you hear the crack of the whip, the tip of a whip is moving at supersonic speeds.

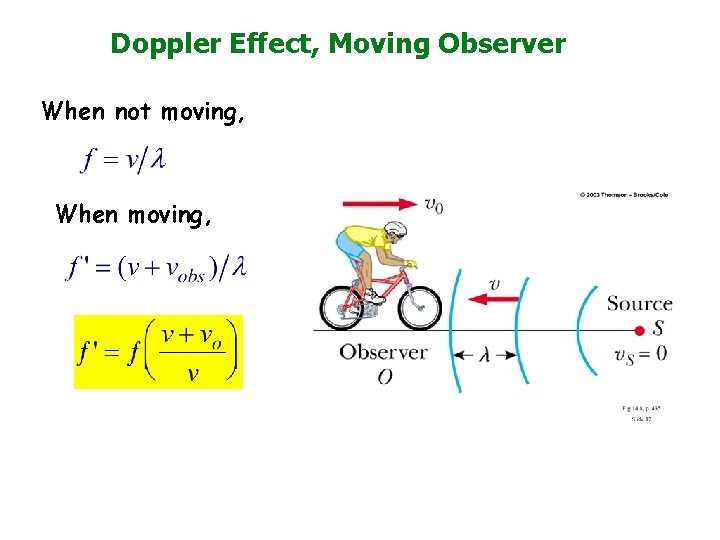
Doppler Effect, Moving Observer When not moving, When moving,

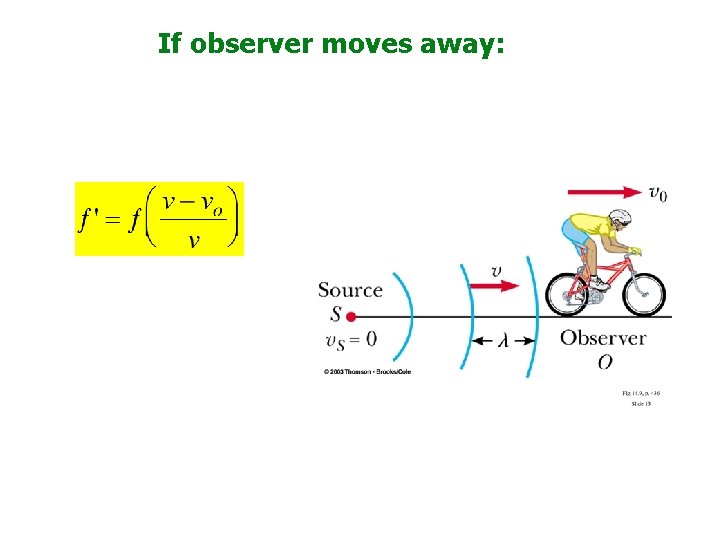
If observer moves away:

Example 1 Mary is riding a roller coaster. Her mother who is standing on the ground behind her yells out to her at a frequency of 1000 Hz, but it sounds like 920 Hz. (v=343 m/s) What is Mary’s speed? 27. 4 m/s

Doppler Effect Source in Motion applet

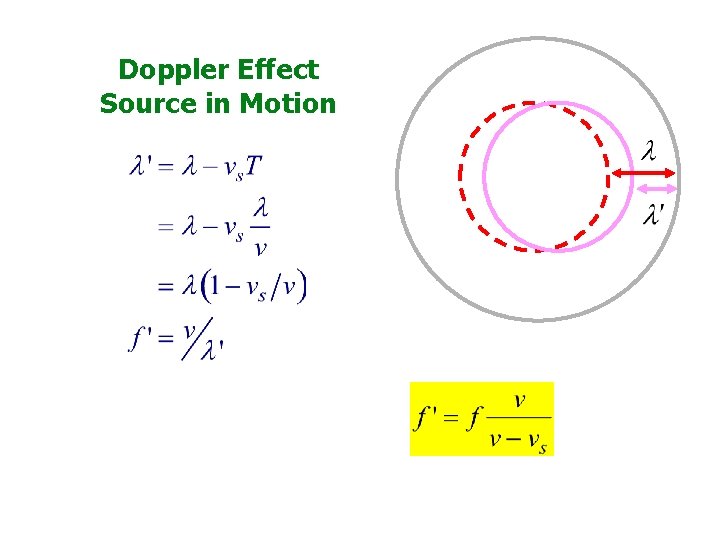
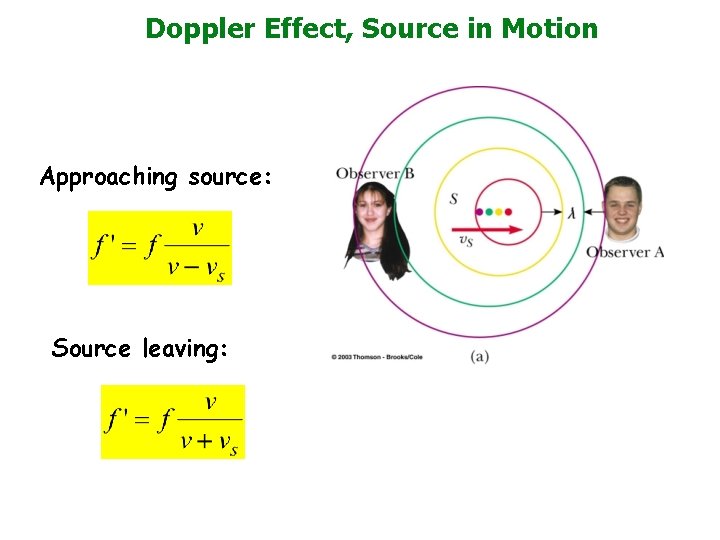
Doppler Effect Source in Motion

Doppler Effect, Source in Motion Approaching source: Source leaving:

Doppler Effect: Both Observer and Source Moving Switch appropriate signs if observer or source moves away Note: 1. Observer is moving toward the source Vo is “+” 2. Observer is moving away from the source Vo is “-” 3. Source is moving toward the observer Vs is “-” 4. Source is moving away from the observer Vs is “+”

Example 2 An train has a brass band playing a song on a flatcar. As the train approaches the station at 21. 4 m/s, a person on the platform hears a trumpet play a note at 3520 Hz. DATA: vsound = 343 m/s a) What is the true frequency of the trumpet? a) 3300 Hz b) What is the wavelength of the sound? b) 9. 74 cm c) If the trumpet plays the same note after passing the platform, what frequency would the person on the platform hear? c) 3106 Hz

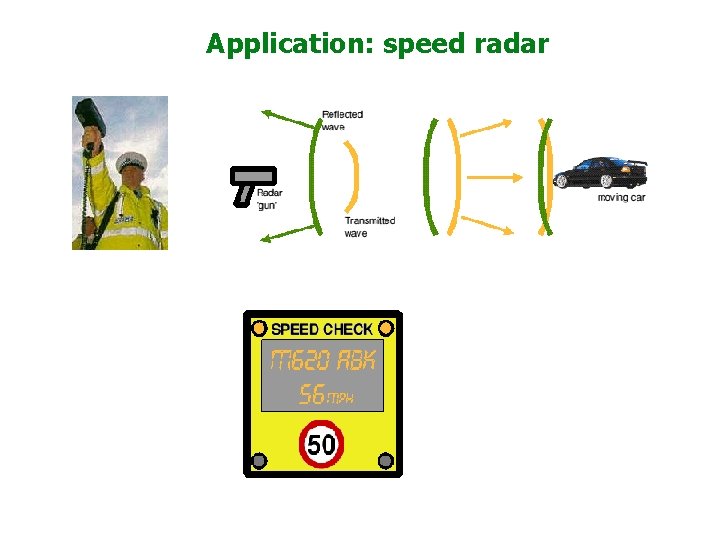
Application: speed radar

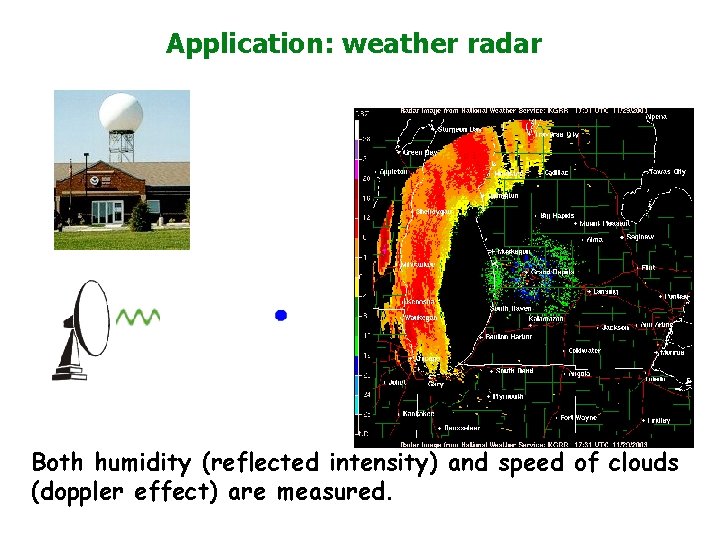
Application: weather radar Both humidity (reflected intensity) and speed of clouds (doppler effect) are measured.

Example 3 At rest, a car’s horn sounds the note A (440 Hz). The horn is sounded while the car moves down the street. A bicyclist moving in the same direction at 10 m/s hears a frequency of 415 Hz. DATA: vsound = 343 m/s. What is the speed of the car? (Assume the cyclist is behind the car) 31. 3 m/s

Example 4 A train has a whistle with a frequency of a 1000 Hz, as measured when both the train and observer are stationary. For a train moving in the positive x direction, which observer hears the highest frequency when the train is at position x=0? Observer A B C D has has velocity VA>0 and has position XA>0. VB>0 and has position XB<0. VC<0 and has position XC>0. VD<0 and has position XD<0.

Example 5 A train has a whistle with a frequency of a 1000 Hz, as measured when both the train and observer are stationary. A train is moving in the positive x direction. When the train is at position x=0, An observer with V>0 and position X>0 hears a frequency: a) > 1000 Hz b) < 1000 Hz c) Can not be determined

Example 6 A train has a whistle with a frequency of a 1000 Hz, as measured when both the train and observer are stationary. A train is moving in the positive x direction. When the train is at position x=0, An observer with V>0 and position X<0 hears a frequency: a) > 1000 Hz b) < 1000 Hz c) Can not be determined

Example 7 A train has a whistle with a frequency of a 1000 Hz, as measured when both the train and observer are stationary. A train is moving in the positive x direction. When the train is at position x=0, An observer with V<0 and position X<0 hears a frequency: a) > 1000 Hz b) < 1000 Hz c) Can not be determined

Example 8: How fast are the police driving? A police siren has a frequency of 550 Hz as the police car approaches you, 450 Hz after it has passed you and is moving away. How fast are the police traveling?

Example 15. 13 How fast are the police driving? (cont. ) SOLVE Because our goal is to find vs, we rewrite Equations 15. 16 as Subtracting the second equation from the first, we get

Example 15. 13 How fast are the police driving? (cont. ) Now we can solve for the speed vs: ASSESS This is pretty fast (about 75 mph) but reasonable for a police car speeding with the siren on.

mary: Applications d d Both Observer and Source moving. d d d © 2015 Pearson Education, Inc. d Slide 15 -44

Doppler Video Plane Video

Shock Waves • A source is supersonic if it travels faster than the speed of sound. • A shock wave travels with the source. If a supersonic source passes an observer, the shock wave produces a sonic boom. • Less extreme examples of shock waves include the wake of a boat and the crack of a whip. © 2015 Pearson Education, Inc. Slide 15 -46

Shock Waves (Sonic Booms) When the source velocity approaches the speed of sound, Video

Section 16. 7 Beats © 2015 Pearson Education, Inc.

Beats • Beat Video

15. 3 Consonance, dissonance, and beats • Harmony is the study of how sounds work together to create effects desired by the composer. • When we hear more than one frequency of sound and the combination sounds good, we call it consonance. • When the combination sounds bad or unsettling, we call it dissonance.

15. 3 Consonance, dissonance, and beats • Consonance and dissonance are related to beats. • When frequencies are far enough apart that there are no beats, we get consonance. • When frequencies are too close together, we hear beats that are the cause of dissonance. • Beats occur when two frequencies are close, but not exactly the same.

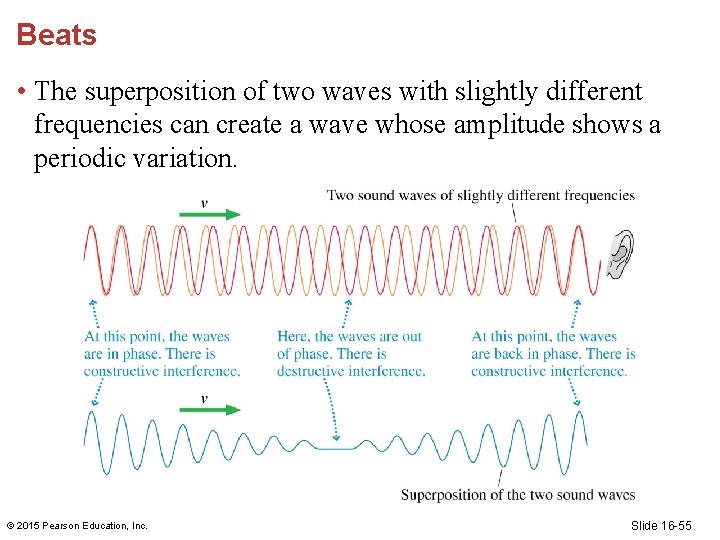
Beats • The superposition of two waves with slightly different frequencies can create a wave whose amplitude shows a periodic variation. © 2015 Pearson Education, Inc. Slide 16 -55

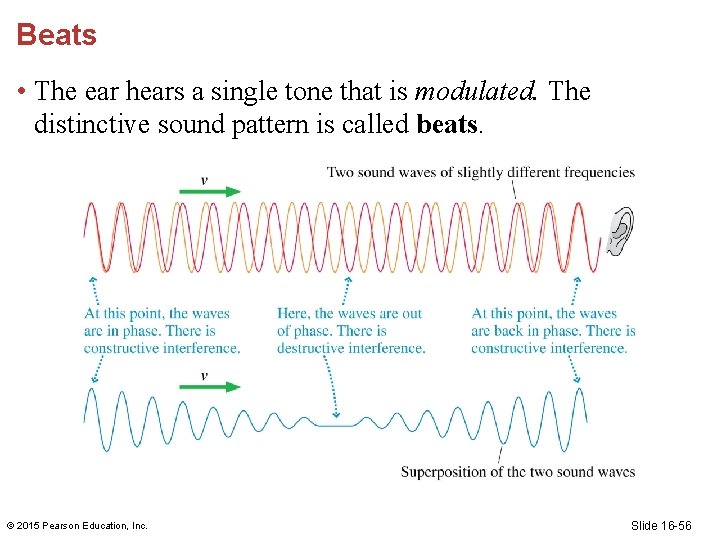
Beats • The ear hears a single tone that is modulated. The distinctive sound pattern is called beats. © 2015 Pearson Education, Inc. Slide 16 -56

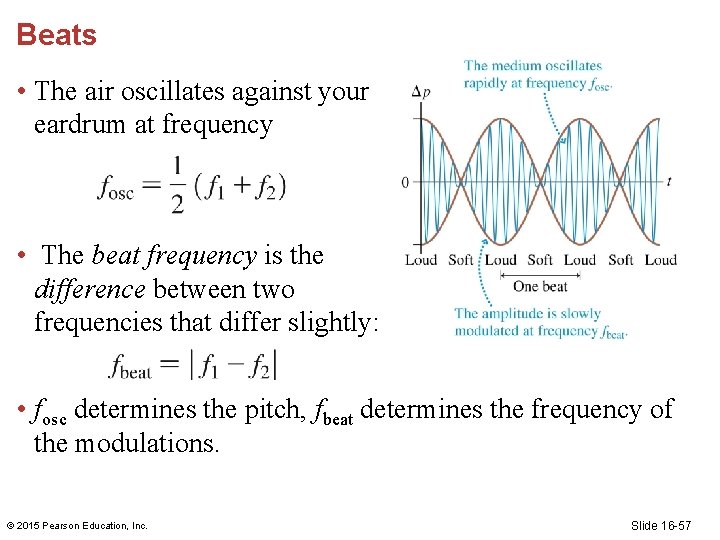
Beats • The air oscillates against your eardrum at frequency • The beat frequency is the difference between two frequencies that differ slightly: • fosc determines the pitch, fbeat determines the frequency of the modulations. © 2015 Pearson Education, Inc. Slide 16 -57

Quick. Check 16. 18 You hear 2 beats per second when two sound sources, both at rest, play simultaneously. The beats disappear if source 2 moves toward you while source 1 remains at rest. The frequency of source 1 is 500 Hz. The frequency of source 2 is A. B. C. D. E. 496 Hz 498 Hz 500 Hz 502 Hz 504 Hz © 2015 Pearson Education, Inc. Slide 16 -58

Quick. Check 16. 18 You hear 2 beats per second when two sound sources, both at rest, play simultaneously. The beats disappear if source 2 moves toward you while source 1 remains at rest. The frequency of source 1 is 500 Hz. The frequency of source 2 is A. B. C. D. E. 496 Hz 498 Hz 500 Hz 502 Hz 504 Hz © 2015 Pearson Education, Inc. Slide 16 -59