AP Chapter 10 Gases Physical Properties of Gases

AP Chapter 10 Gases

Physical Properties of Gases Noble Gases Diatomic gases Gaseous compounds of Nonmetals n n n Will fill any container Highly compressible Form homogeneous mixtures

Characteristics: n n n Amount: measured in moles (n) Temperature: measured in Kelvin (K) Volume: measured in liters Simple gas laws can use milliliters n Pressure: measured in 1 atmosphere (atm) 760 mm Hg 760 torr 14. 69 psi 101, 325 Pascals (N/m 2) 1. 01325 Bar

Barometer was invented in 1643 by Evangelista Torricelli (Torr) Manometer is a device used to measure pressure difference between a gas and barometric pressure. is Standard Temperature Pressure (STP) 0 o. C and 1 atm. Molar volume is the volume of one mole of gas at specific temperatures. STP – molar volume is 22. 4 L 25 o. C – molar volume is 24. 5 L

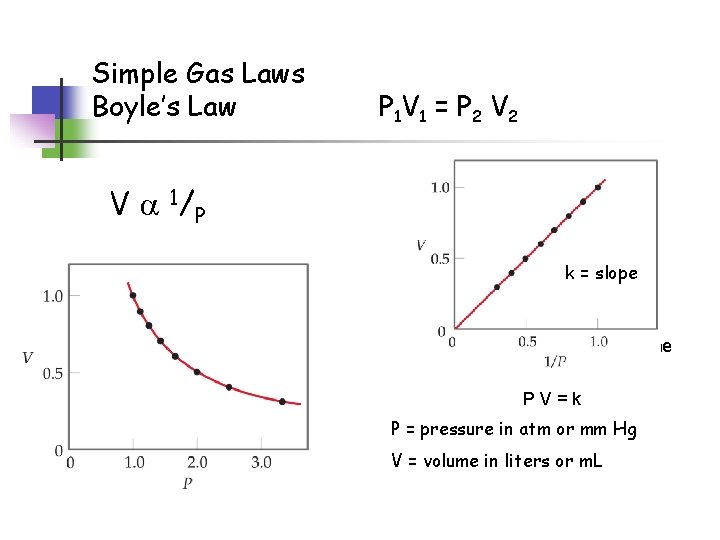
Simple Gas Laws Boyle’s Law P 1 V 1 = P 2 V a 1/ P k = slope When graphing V and 1/P, the slope of the line = k PV=k P = pressure in atm or mm Hg V = volume in liters or m. L

Charles Law V 1 = V 2 T 1 T 2 A plot of all gas extrapolated to a volume of zero, occurs at 0 K, (-273 o. C) Absolute Zero Va. T V = volume in liters or m. L T = temperature in Kelvin

Pressure Temperature Law P 1 = P 2 T 1 T 2 Pressure Pa. T P = pressure in atm or mm Hg T = temperature in Kelvin Temperature

Avogadro’s Law V 1 = V 2 N 1 N 2 Va N Volume Avogadro’s Hypothesis: Equal volumes of gas at the same temperature and pressure contain equal number of particles. Moles V = volume in liters or m. L N = number of moles

General Gas Law combines all of the simple gas laws into one. P 1 V 1 = P 2 V 2 T 1 N 1 T 2 N 2 P = pressure in atm or mm Hg V = volume in liters or m. L T = temperature in Kelvin N = moles

Ideal Gas Law PV=n. RT P = pressure in atm V = volume in liters n = number of moles R = gas constant 0. 08206 T = temperature in Kelvin atm L/ mol K An Ideal gas is hypothetical, it assumes that the gas atoms or molecules have no volume and there is no interactions between particles.

Calculate the volume of H 2(g) measured at 26 o. C and 751 mm Hg, required to react with 28. 5 L of CO(g) measured at 0 o. C and 760 mm Hg in the following reaction: CO (g) + H 2 (g) C 3 H 8 (g) + H 2 O (g) Remember Avogadro’s hypothesis!

What volume of N 2 (g) measured at 735 mm Hg and 26 o. C is produced when 70. 0 g of Na. N 3 (s) is decomposed in an air bag. Na. N 3 (s) Na (s) + N 2 (g)

A sample of methane gas having a volume of 2. 80 L at 25 o. C and 1. 65 atm was mixed with a sample of O 2 (g) having a volume of 35. 0 L at 31 o. C and 1. 25 atm. The mixture was then ignited to form CO 2 (g) and H 2 O (g). Calculate the volume of CO 2 formed at a pressure of 2. 50 atm and 125 o. C. CH 4 (g) + O 2 (g) CO 2 (g) + H 2 O (g)

The Ideal Gas Law can be converted to many forms to find other properties of gases. Grams /molar mass = moles PV= grams /molar mass R T Molar mass = grams R T/ d. RT/ = P M PV

A gas has a pressure of 1. 10 atm at a temperature of 300 K and a volume of 2. 79 L. It has a mass of 2. 00 g. What is it’s molar mass? Molar mass = grams R T / P V

To find density of a gas Density = Molar mass = mass /volume grams R T / PV Molar mass = (grams/volume)(R T/P) Molar mass = d= d. RT M P/ RT / P

d= MP / RT What is the density of O 2 (g) at 298 K and 0. 987 atm?

Dalton’s Law of Partial Pressures – For a mixture of gases, in a container, the total pressure exerted is the sum of the pressures that each gas would exert if it were alone. PT = P 1 + P 2 + P 3. . . P = n(RT/V) PT = (n 1 + n 2 + n 3. . . )(RT/V)

Mole fraction c = NA NT = PA PT c (chi) = VA VT A = individual gas T = total gas mixture Important characteristics of an ideal gas • Pressure is not exerted by identity of gas • Volume of individual gas particles is unimportant • Force of individual gas particles is unimportant

What is the pressure exerted by a mixture of 1. 0 g H 2 (g) and 5. 0 g He (g) in a volume of 5. 0 L and a temperature of 293 K? What are the partial pressures of H 2 and He in the mixture?

Mixtures of Helium and oxygen can be used in scuba diving tanks to help prevent “the bends”. For a particular dive, 46 L He at 25 o. C and 1. 0 atm and 12 L of O 2 at 25 o. C and 1. 0 atm were pumped into a tank with a volume of 5. 0 L. Calculate the partial pressure of each gas and the total pressure in the tank at 25 o. C. (hint: calculate the total moles and pressure of each, then total pressure)

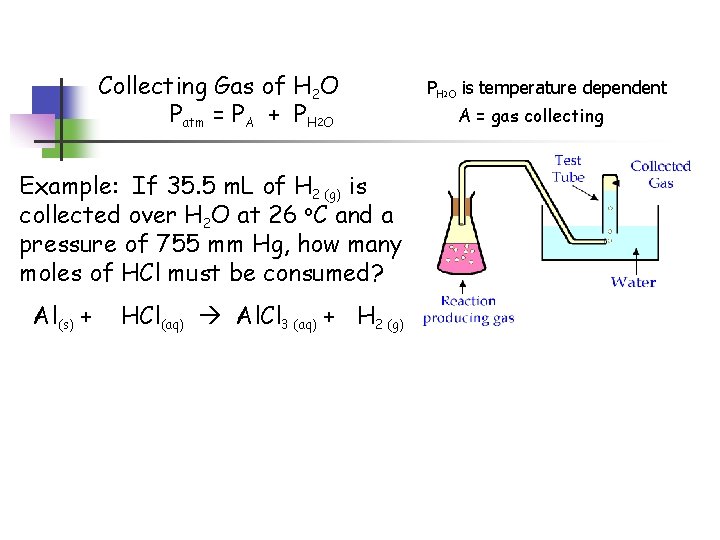
Collecting Gas of H 2 O Patm = PA + PH 2 O Example: If 35. 5 m. L of H 2 (g) is collected over H 2 O at 26 o. C and a pressure of 755 mm Hg, how many moles of HCl must be consumed? Al(s) + HCl(aq) Al. Cl 3 (aq) + H 2 (g) PH 2 O is temperature dependent A = gas collecting

Determination of Gas Constant Lab Mg (s) + HCl(aq) Mg. Cl 2 (aq) + H 2 (g) We want to collect exactly 30 m. L of H 2 (g) How much Mg do we use? (exactly) How much HCl do we use? (use excess!) Temp = Pressure =

Kinetic Theory of Molecular Motion n n A gas is composed of a very large number of extremely small (molecules or atoms) particles, in constant, random, straight line motion. The total volume of the gas molecules is negligible compared to the volume used (mostly empty space). Molecules collide with each other and the walls of the container. Collisions occur very rapidly and are elastic (collisions result in pressure). There are no forces of attraction between the molecules. Molecules may gain or lose energy, but the total energy of the gas remains constant. KE = ½ m v 2

This is an illustration of the path of one gas molecule over time.

Kinetic energy depends only on temperature. If gases have an equal number of moles and their temperature is the same, they have equal amount of Kinetic energy. KE = ½ m v 2 All molecules do not travel at the same speed! It is dependent on the mass of the molecule.

When molecules do not have the same temperature, the higher the temperature (KE), the faster the molecules.

3 cars are going down the highway. One at 40 mph, one at 50 mph, and one at 60 mph. What is the average speed (u)?

Root – mean – square velocity (urms) is weighted toward molecules with higher speeds. urms = u 2 From the car analogy, urms = The formula is weighted toward molecules with higher speeds. mean t o o r e h t To find gas a f o y t i c o l square ve R = 8. 3145 J/mol K urms = meters/sec urms = __ 3 RT M M = molar mass in kg/mole T = Kelvin

Find the average speed of He (g) at 25 o. C

Which is the greater speed, that of a bullet from a high–powered M-16 rifle (2180 mph) or the root– mean–square speed of H 2 (g) molecules at 25 o. C?

Kinetic energy of a gas can be calculated KE = ½ m v 2 (Per molecule) K E = ( 3/ 2) R T (Per mole) R = 8. 3145 J/mol K T = Kelvin No ook b t x e t in t

Pressure of a gas is caused by molecules hitting the walls of the container. P = ( 1/ 3 ) ( n / V ) M u 2 = average of the squares of all the molecule speeds n = number of molecules M = mass of one molecule ook xt b e t n i t No

Diffusion is the migration of a gas through other gases. Effusion is the rate of passage of a gas through an orifice (tiny hole). Graham’s Law of Effusion __ Rate of Effusion. A = urms A = Rate of Effusion B urms B 3 R T/ __ 3 RT m. A / = m. B When using Graham’s Law, always change information to rates before working with. m. B m. A

2. 2 x 10 -4 mol N 2 (g) effuses through a tiny hole in 105 seconds. How much H 2 (g) would effuse through the hole in the same amount of time?

A sample of Kr (g) escapes through a tiny hole in 87. 3 sec. An unknown gas requires 42. 9 seconds for the same amount. What is the molecular mass of the unknown gas?

Non – Ideal Gases (Real Gases) PV = n. RT works well at low to moderate pressures and moderate to high temperatures. Outside of that, adjustments must be made to the formula. At high pressures or low temperatures, gas turns into liquids. Van der Walls equation: [P + a(n/V)2] (V – nb) = n R T - - - The ideal gas particles have no forces of attraction but Real gas particles do have some forces of attraction which reduce the pressure a(n/V)2 = (proportionality constant) (moles/volume)2 The ideal gas law describes gas which the particles are volumeless but Real gas particles take up space nb = (moles)(constant for that gas) See page 429

Atmospheric layers are based on temperature which fluctuates. Pressure constantly decreases with altitude.

Composition of the atmospheric gases Component mole fraction N 2 O 2 Ar CO 2 Ne He CH 4 Kr H 2 NO Xe 0. 78084 0. 20948 0. 00934 0. 000345 0. 00001818 0. 00000524 0. 00000168 0. 00000114 0. 0000005 0. 000000087 These numbers reflect the atmosphere at sea level, and with H 2 O disregarded.

Air pollution comes from 2 main sources 1. transportation 2. electricity production 1. Produces CO, CO 2, NO 2, and unburned fuel NO from cars NO 2 in the atmosphere NO 2 + hv NO + O 2 O 3 O 2 + energy + O O + H 2 O 2 OH OH + NO 2 HNO 3 (acid rain) 2 NO 2 + H 2 O NHO 2(aq) + HNO 3 (aq) 2 SO 2 + O 2 2 SO 3 + H 2 O H 2 SO 4 (aq) (acid rain) Photochemical smog (NO 2 and O 3) combined with sunlight (hv) cause chemical pollution

2. Pollutants from electricity production (especially coal containing sulfur) S + O 2 SO 2 will eventually H 2 SO 4 Chimney scrubbers blow Ca. CO 3 into combustion chambers of coal Ca. CO 3 Ca. O (s) + CO 2 (g) Ca. O (s) + SO 2 (g) Ca. SO 3 (s) which can be disposed of

Which gas has the greatest Kinetic energy?

Ideal Gas Law Bottle Lab The average molar mass of “air” is 29. 0 g/mol Room temp. = Atmospheric pressure =

room temp volume of bottle pressure 1 Trial 1 etc 2 Mass of bottle, syringe + air use scale to measure 3 Volume of air in syringe look at 4 Pressure inside bottle measure then calculate (pressure on gauge + current pressure)(1 atm/14. 69 psi)= 5 mass of air calculate (Q#2) m= P V molar mass/ 6 mass of bottle +syringe RT calculate (Q#3) column 2 – column 5 = 7 moles of air in bottle n = mass of air/molar mass of air pressure inside/ 8 pressure to mole ratio moles of air

Questions + calculations 1 pressure inside bottle = column 4 2 mass of air = column 5 3 mass of bottle + syringe = column 2 – column 5 4 moles of air = column 7 5 ratio of atm/mole = column 4/column 7 6 graph y axis = pressure (atm) x axis = moles of air (should end up a straight line y = mx + b) 7 theoretical atm/mole ratio = R T/V 8 compare Calculate % accuracy

Avogadro’s Law: At the same temperature and pressure, equal volumes of gases contain the same number of particles.