AP Calculus AB Chapter 3 Section 1 Extrema

AP Calculus AB Chapter 3, Section 1 Extrema on an Interval 2013 - 2014

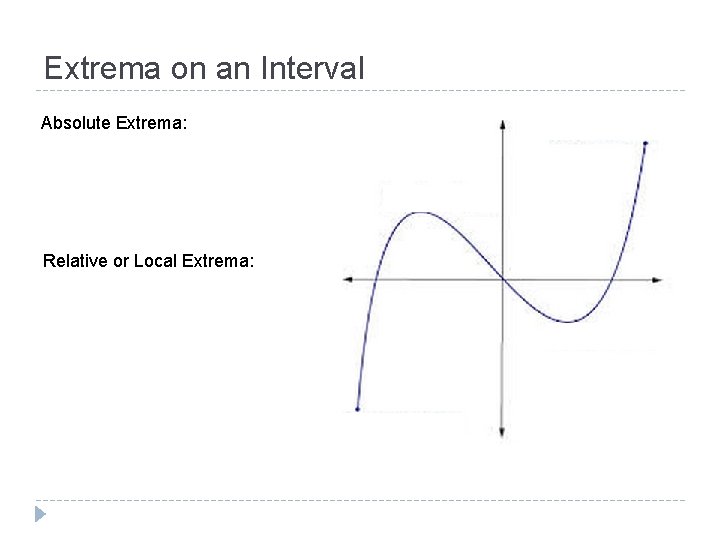
Extrema on an Interval Absolute Extrema: Relative or Local Extrema:

Extreme Value Theorem � If f is continuous on a closed interval [a, b], the f has both an absolute minimum and an absolute maximum on the interval. � The minimum and maximum of a function on an interval are the extreme values, or extrema, of the function on the interval. They are also called the absolute minimum or absolute maximum on the interval, respectively.

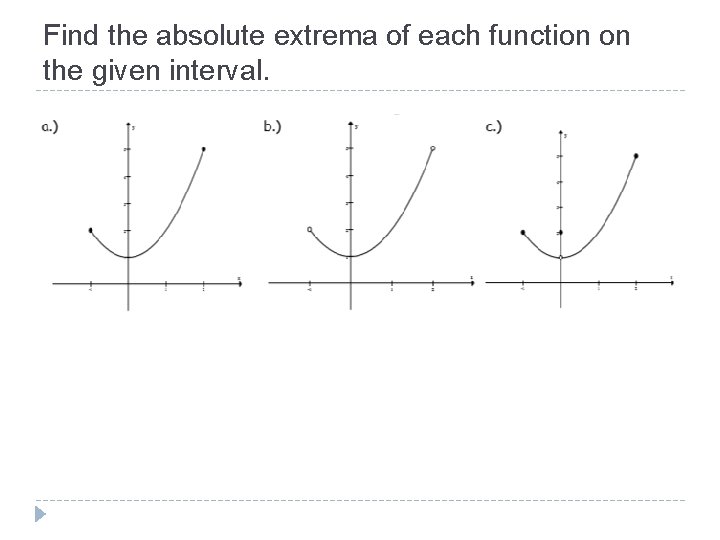
Find the absolute extrema of each function on the given interval.

Critical Numbers �

Definition of a Critical Number �

Critical Numbers � If f(x) is a smooth curve, there are three possible outcomes that can occur at a critical number: � An absolute or relative maximum can occur, � An absolute or relative minimum can occur, � A point of inflection can occur

Find any critical numbers of the function �

Finding Extrema on a Closed Interval � Guidelines � Find for finding extrema on a closed interval: the critical numbers of f in (a, b). � Evaluate f at each critical number in (a, b). � Evaluate f at each endpoint of [a, b]. � The least of these values is the minimum, the greatest is the maximum.

Chapter 3. 1 Homework � Pg. 169 – 171, #’s: 3, 7, 19, 27, 41, 61