AP Calculus AB Area Under a Curve Find

AP Calculus AB

Area Under a Curve Find the area of the region bounded by y = f(x), the x-axis, x = a, and x = b. Approximate the area by creating rectangles of equal width whose endpoints are on f(x). n = # of rectangles Each left endpoint is on f(x) Each right endpoint is on f(x) This under-estimates the area under the curve… This over-estimates the area under the curve… We call it the Lower Sum. We call it the Upper Sum. Each method is called a Riemann Sum.

How do we make these approximations for the area under a curve more accurate? Use more rectangles. (Always choose whichever sum involves right endpoints. ) The Limit Definition for finding the area under a curve: or

Find the area beneath interval [1, 3]. (above the x-axis) in the a. Use 1 rectangle. b. Use 2 rectangles. If a specific number of rectangles is given, it is often easier to find the area without using sigma!

Find the area beneath interval [1, 3]. (above the x-axis) in the c. Use the limit definition.

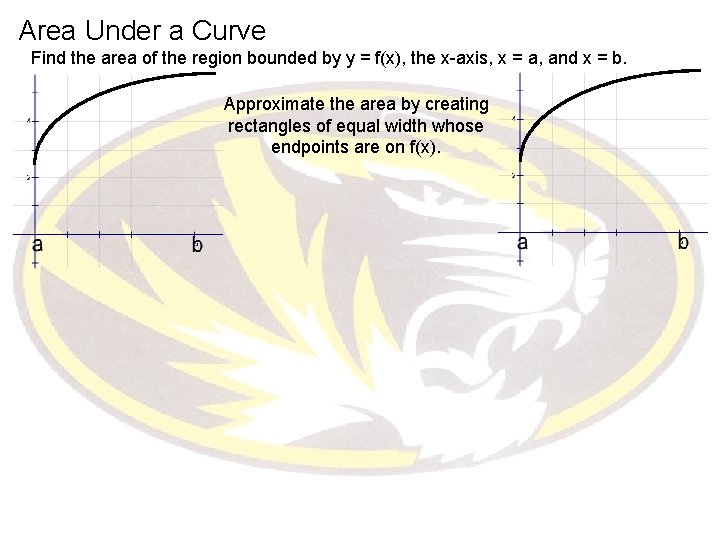
Area Under a Curve Find the area of the region bounded by y = f(x), the x-axis, x = a, and x = b. Approximate the area by creating rectangles of equal width whose endpoints are on f(x).

How do we make these approximations for the area under a curve more accurate? The Limit Definition for finding the area under a curve:

Find the area beneath interval [1, 3]. (above the x-axis) in the a. Use 1 rectangle. b. Use 2 rectangles.

Find the area beneath interval [1, 3]. (above the x-axis) in the c. Use the limit definition.