AP Calculus 4 2 Food for Thought What

AP Calculus 4. 2 Food for Thought What is the possible relationship between f(a), f(b), and f(c) in Rolle’s Theorem? What is the possible relationship between f(a), f(b), and f(c) in the Mean Value Theorem? If a biker travels 45 km in 3 hours, can we guarantee that her speedometer must have read 15 km/hr at least once during the trip? Can we guarantee it will read 12 km/hr at least once during her trip? How about 18 km/hr? Explain. Investigate the function . How does this demonstrate that the conclusion of Rolle’s Theorem may not hold if a function is not differentiable everywhere? Show to use the Intermediate Value Theorem and Rolle’s Theorem to determine that has exactly one real root and that root is between -1 and 0. 6. Why is the requirement f(a) = f(b) a crucial part of Rolle’s Theorem? 7. How is the Intermediate Value Theorem related to the Mean Value Theorem? 8. Even though it doesn’t mention them, in what way are parallel lines an important part of the Mean Value Theorem? 9. Give an example of a problem situation in which the Mean Value Theorem can be interpreted as saying that there is a number at which the instantaneous rate of change is equal to the average rate of change over an interval. 10. Suppose that f(0) = -3 and f ’(x) ≤ 5 for all values of x. How large can f(2) possibly be?

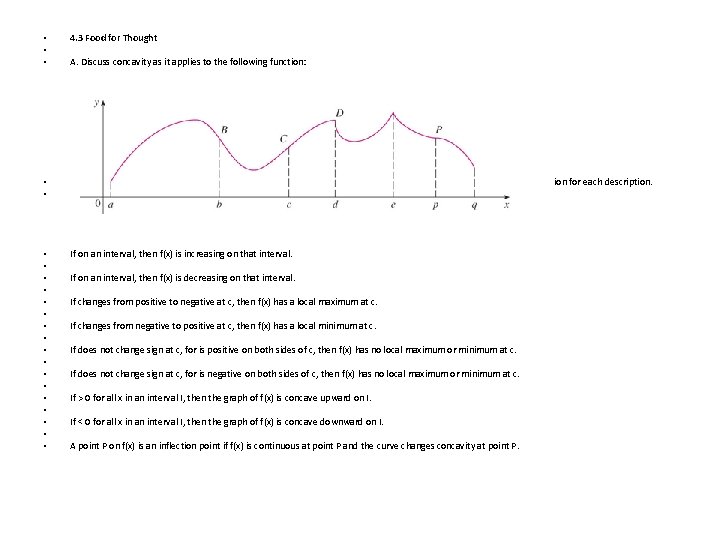
• • • 4. 3 Food for Thought A. Discuss concavity as it applies to the following function: • • B. Determine a function that fits each description. Provide labels for clarification where necessary. Use a different function for each description. • • • • • If on an interval, then f(x) is increasing on that interval. If on an interval, then f(x) is decreasing on that interval. If changes from positive to negative at c, then f(x) has a local maximum at c. If changes from negative to positive at c, then f(x) has a local minimum at c. If does not change sign at c, for is positive on both sides of c, then f(x) has no local maximum or minimum at c. If does not change sign at c, for is negative on both sides of c, then f(x) has no local maximum or minimum at c. If > 0 for all x in an interval I, then the graph of f(x) is concave upward on I. If < 0 for all x in an interval I, then the graph of f(x) is concave downward on I. A point P on f(x) is an inflection point if f(x) is continuous at point P and the curve changes concavity at point P.

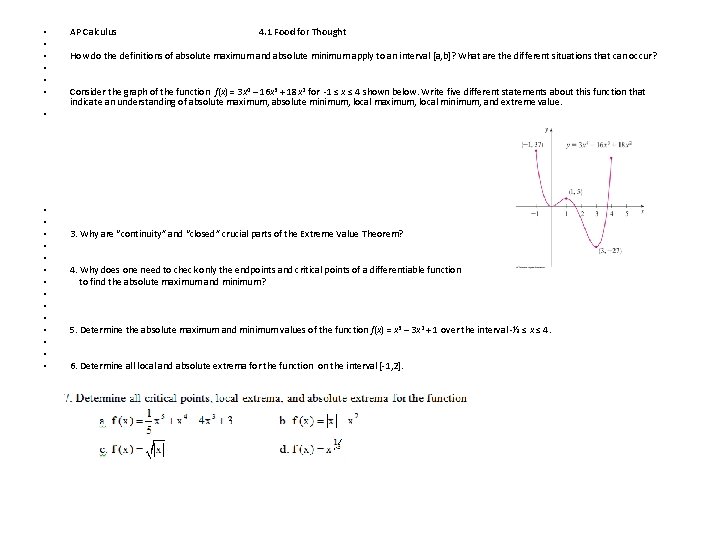
• AP Calculus 4. 1 Food for Thought How do the definitions of absolute maximum and absolute minimum apply to an interval [a, b]? What are the different situations that can occur? Consider the graph of the function f(x) = 3 x 4 – 16 x 3 + 18 x 2 for -1 ≤ x ≤ 4 shown below. Write five different statements about this function that indicate an understanding of absolute maximum, absolute minimum, local maximum, local minimum, and extreme value. • • • • • 3. Why are “continuity” and “closed” crucial parts of the Extreme Value Theorem? 4. Why does one need to check only the endpoints and critical points of a differentiable function to find the absolute maximum and minimum? 5. Determine the absolute maximum and minimum values of the function f(x) = x 3 – 3 x 2 + 1 over the interval -½ ≤ x ≤ 4. 6. Determine all local and absolute extrema for the function on the interval [-1, 2]. 7. Determine all critical points, local extrema, and absolute extrema for the function a. b. c. d. • • •