AOSS 401 Geophysical Fluid Dynamics Atmospheric Dynamics Prepared


























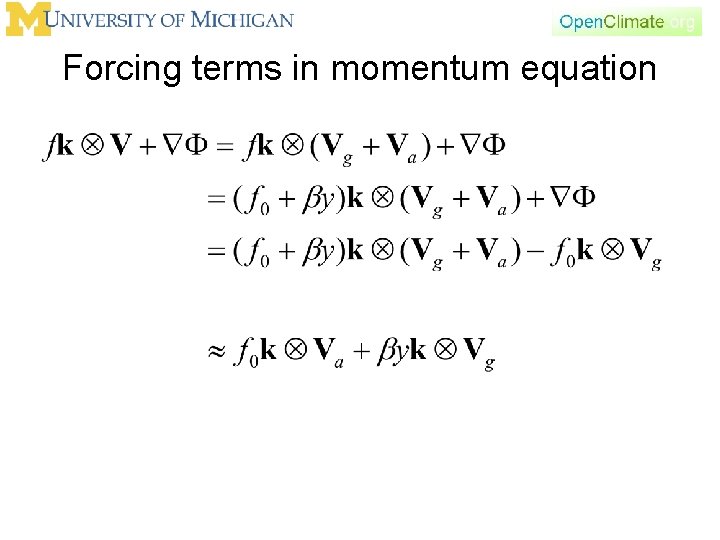









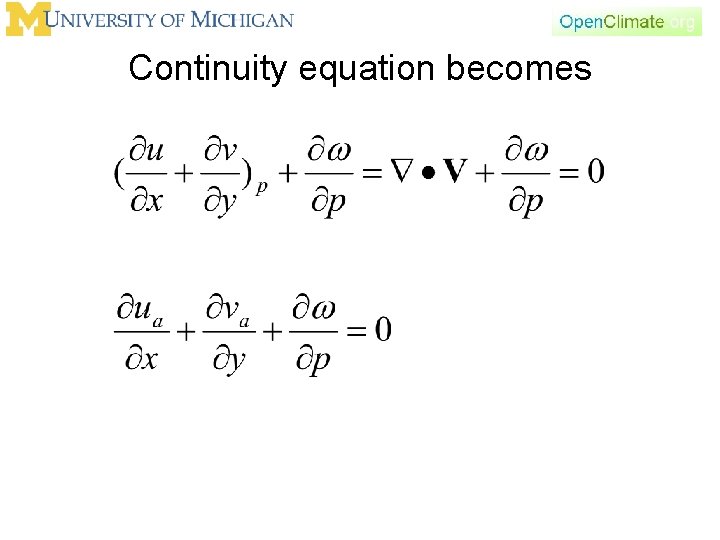































- Slides: 82

AOSS 401 Geophysical Fluid Dynamics: Atmospheric Dynamics Prepared: 20131112 Quasi-geostrophic equations Richard B. Rood (Room 2525, SRB) rbrood@umich. edu 734 -647 -3530 Cell: 301 -526 -8572

Class News • Ctools site (AOSS 401 001 F 13) • Second Examination on December 10, 2013 • Homework – Key your eyes open

Weather • National Weather Service – Model forecasts: • Weather Underground – Model forecasts: • NCAR Research Applications Program

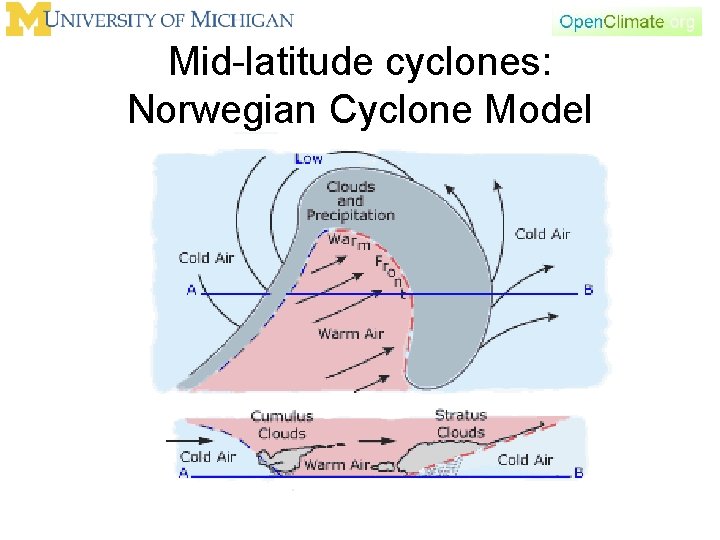
Mid-latitude cyclones: Norwegian Cyclone Model

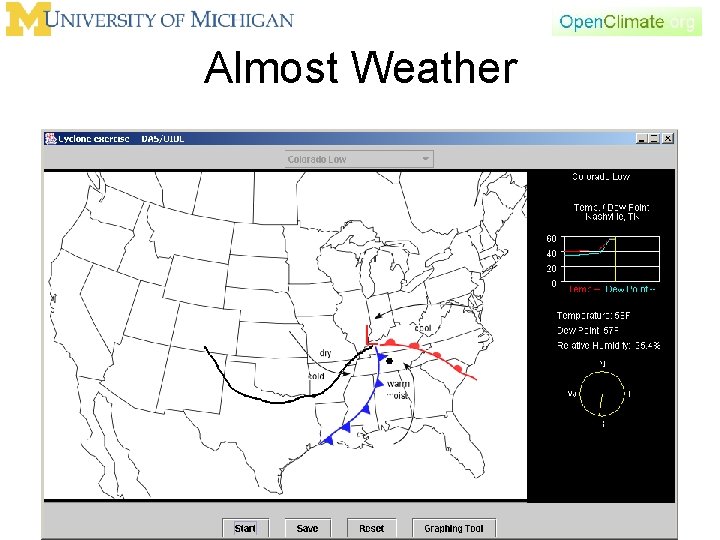
Almost Weather

Mid-latitude cyclones: Norwegian Cyclone Model • http: //www. srh. weather. gov/jetstream/syno ptic/cyclone. htm

Outline • Vorticity in Atmosphere Redux • In Class Problem • Scaling Equations in Pressure Coordinates – Quasi-geostrophic Equations • Quasi-geostrophic Vorticity Equations

Vorticity Equation DIVERGENCE TILTING SOLENOIDAL or BAROCLINIC Changes in relative vorticity are caused by: • Divergence • Tilting • Gradients in density on a pressure surface • Advection

Scale factors for “large-scale” mid-latitude

Terms in Vorticity Equation Time rate of change Horizontal advection Vertical advection Divergence Tilting Planetary vorticity advection Solenoidal term

Assume balance among terms of 10 -10 s-2

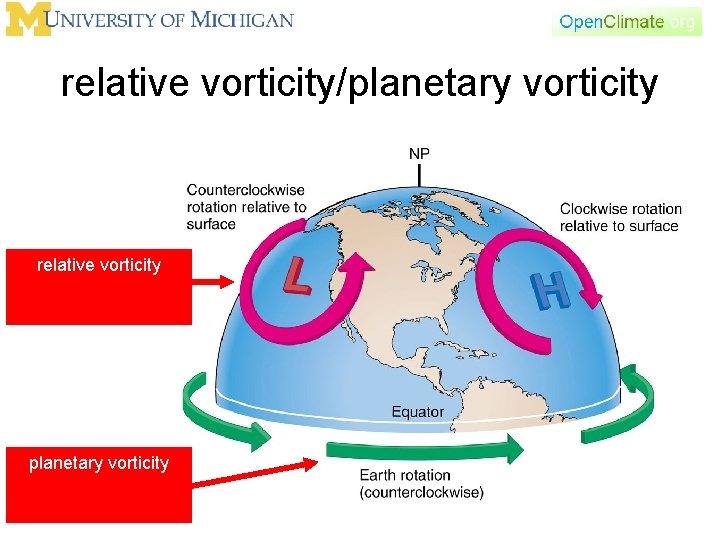
Relative and planetary vorticity • Planetary vorticity is cyclonic is positive vorticity • Planetary vorticity, in middle latitudes, is usually larger than relative vorticity • A growing cyclone “adds to” the planetary vorticity. – Lows are intense • A growing anticyclone “opposes” the planetary vorticity. – Highs are less intense

relative vorticity/planetary vorticity relative vorticity planetary vorticity

Use our simple form of potential vorticity From scaled equation, with assumption of constant density and temperature.

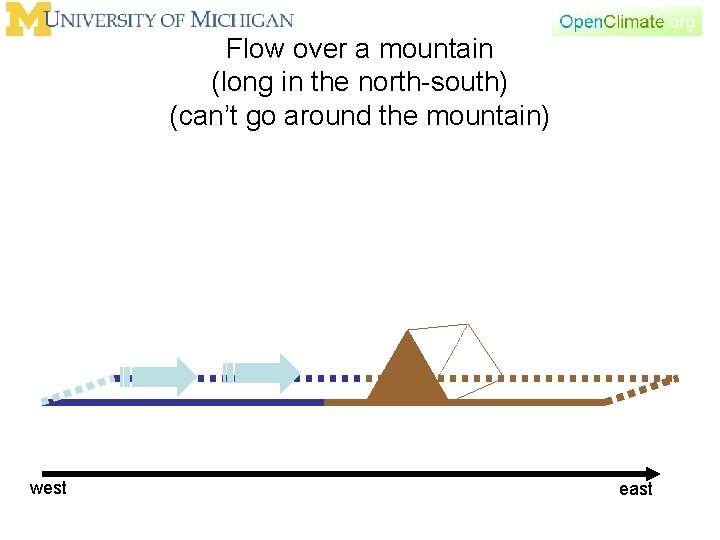
Flow over a mountain (long in the north-south) (can’t go around the mountain) west east

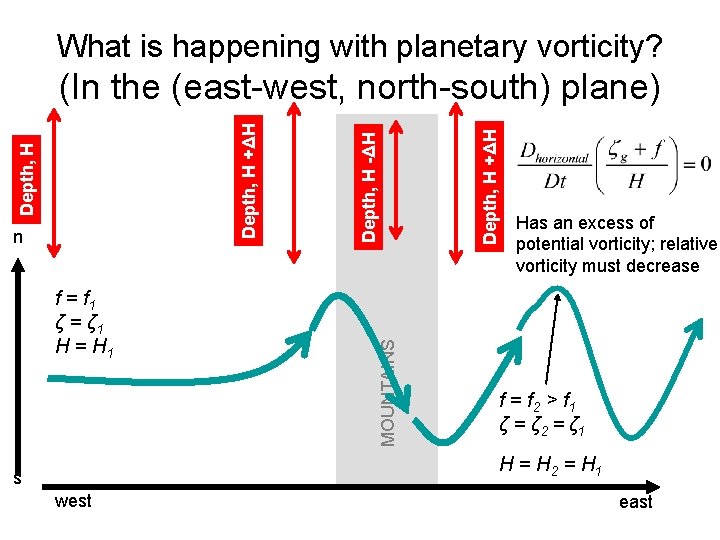
What is happening with planetary vorticity? f = f 1 ζ = ζ 1 H = H 1 MOUNTAINS Depth, H +ΔH n Depth, H -ΔH Depth, H +ΔH (In the (east-west, north-south) plane) Has an excess of potential vorticity; relative vorticity must decrease f = f 2 > f 1 ζ = ζ 2 = ζ 1 H = H 2 = H 1 s west east

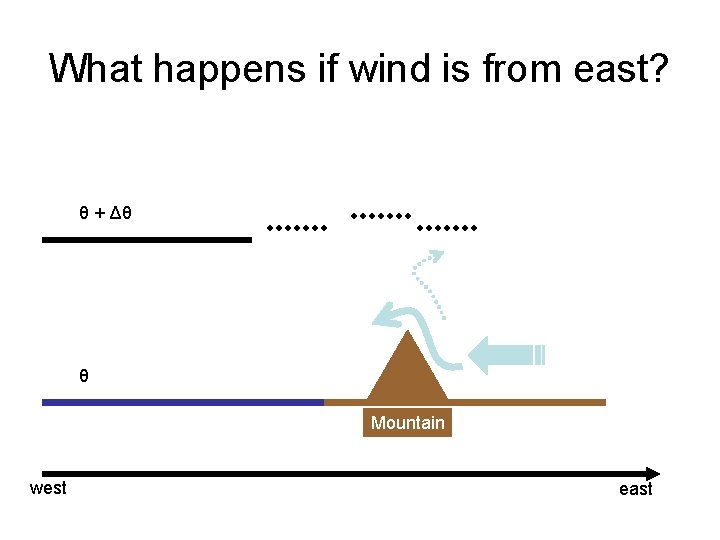
What happens if wind is from east? θ + Δθ θ Mountain west east

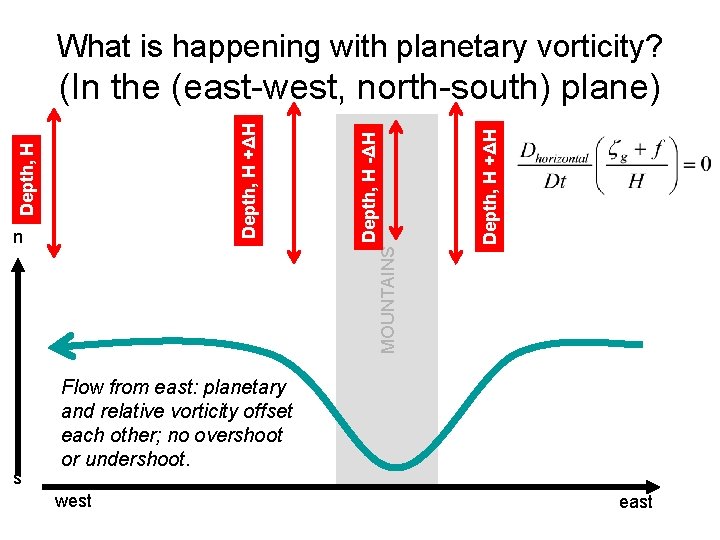
What is happening with planetary vorticity? s Depth, H +ΔH MOUNTAINS n Depth, H -ΔH Depth, H +ΔH (In the (east-west, north-south) plane) Flow from east: planetary and relative vorticity offset each other; no overshoot or undershoot. west east

Outline • Vorticity in Atmosphere Redux • In Class Problem • Scaling Equations in Pressure Coordinates – Quasi-geostrophic Equations • Quasi-geostrophic Vorticity Equations

Equations of motion

Scale factors for “large-scale” mid-latitude

Scale of relative vorticity

Compare relative vorticity to planetary vorticity and to divergence Flow is rotationally dominated, but divergence is crucial to understanding the flow.

From the scale analysis we introduced the nondimensional Rossby number A measure of planetary vorticity compared to relative vorticity. A measure of the importance of rotation.

Scale analysis of equations in pressure coordinates • Start: – horizontal flow is approximately geostrophic – vertical velocity much smaller than horizontal velocity

horizontal flow is approximately geostrophic • L, length scale, is small compared to the radius of the Earth • In the calculation of geostrophic wind, assume f is constant; f = f 0

horizontal flow is approximately geostrophic

We will scale the material derivative Ignore // small This is for use in the advection of temperature and momentum. ω comes from div(ageostrophic wind)

Variation of Coriolis parameter • L, length scale, is small compared to the radius of the Earth • In the calculation of geostrophic wind, assume f is constant; f = f 0 • We cannot assume f is constant in the Coriolis terms…

Variation of Coriolis parameter

Variation of Coriolis parameter Scale of first two terms.

Equations of motion in pressure coordinates (using Holton’s notation)

Wait, wait … • A few slides ago didn’t you assume that f was constant when you calculated the geostrophic wind. But then one slide later say that you could not assume f was constant when you calculated the Coriolis term. • Why yes, that’s what I did.

Forcing terms in momentum equation def’n of the full wind approx of coriolis parameter Use definition of geostrophic wind in the pressure gradient force
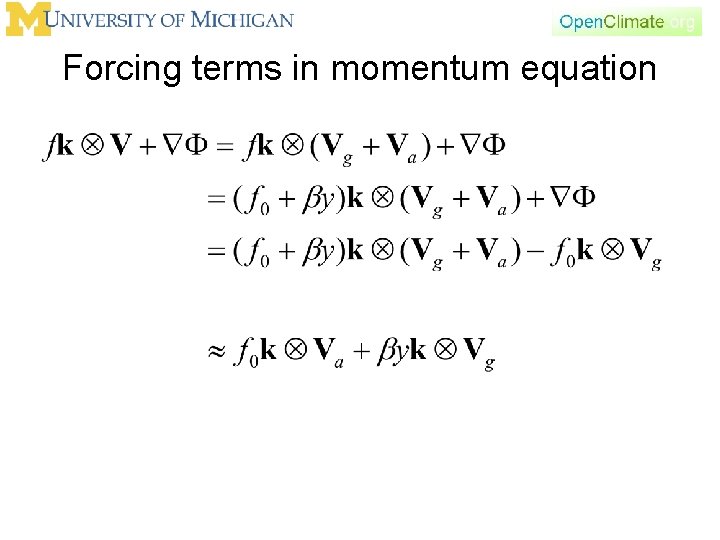
Forcing terms in momentum equation

Approximate horizontal momentum equation This equation states that the time rate of change of the geostrophic wind is related to 1. the coriolis force due to the ageostrophic wind and 2. the part of the coriolis force due to the variability of the coriolis force with latitude and the geostrophic wind. Both of these terms are smaller than the geostrophic wind itself.

Wait, wait! • My head is spinning. I learned, what, just a month ago that the geostrophic wind was a diagnostic, and that in order for there to be any acceleration of the wind that the wind had to be ageostrophic. • Why yes you did. But now we are considering something that is only quasi-geostrophic. We know that we really, really need to know those things that make things “not geostrophic, ” but “almost geostrophic. ” • I’d feel better if I could just work on a problem for a few minutes.

Outline • Vorticity in Atmosphere Redux • In Class Problem • Scaling Equations in Pressure Coordinates – Quasi-geostrophic Equations • Quasi-geostrophic Vorticity Equations

In class problems • Group (Thermal) – Scott – Anna – James – Kevin – Trent • Group (Perturb) – John – Ross – Rachel – Jordan – Justin – Alex

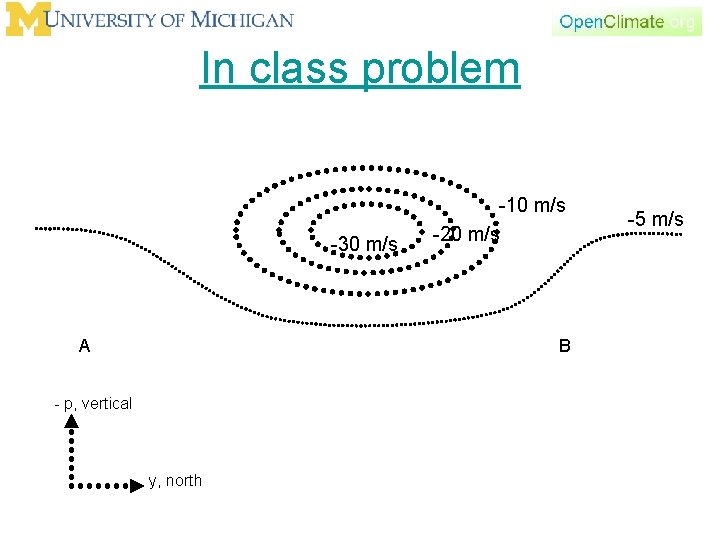
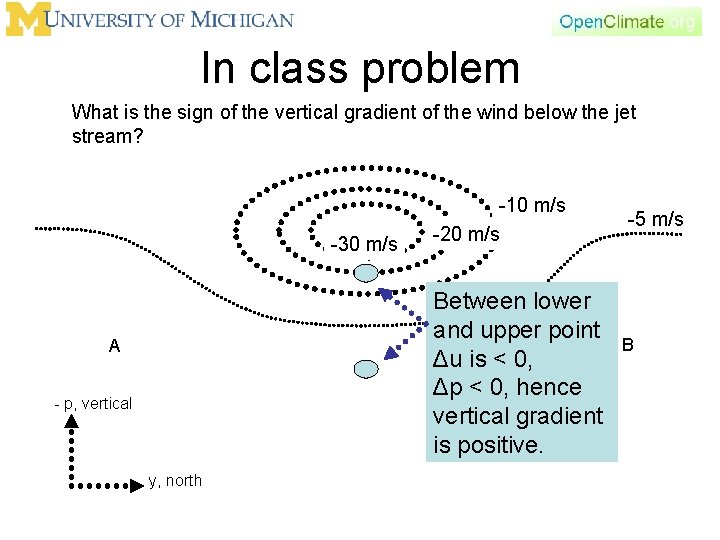
In class problem: Thermal wind Refer to the figure. This figure shows a jet stream in the northern hemisphere, upper troposphere. The direction is easterly, from the east. We saw that in a hydrostatic atmosphere the vertical gradient of the geostrophic wind, was related to the horizontal gradient of temperature. That is thermal wind relationship. What is the sign of the vertical gradient of the wind below the jet stream? With this information, is point A warmer or colder than point B ? Where are the temperature gradients strongest ? Be sure to justify your decisions.

In class problem -30 m/s A -10 m/s -20 m/s B - p, vertical y, north -5 m/s

In class problem: Perturbation a) Expand the material derivative using the definition of the velocity field given in the problem. b) Write an equation for the time rate of change (partial derivative in t) of the zonal mean velocity. (The partial in t for the perturbation velocity should not appear. )

Outline • Vorticity in Atmosphere Redux • In Class Problem • Scaling Equations in Pressure Coordinates – Quasi-geostrophic Equations • Quasi-geostrophic Vorticity Equations

return to the geostrophic wind • L, length scale, is small compared to the radius of the Earth • In the calculation of geostrophic wind, assume f is constant; f = f 0

divergence of the horizontal wind
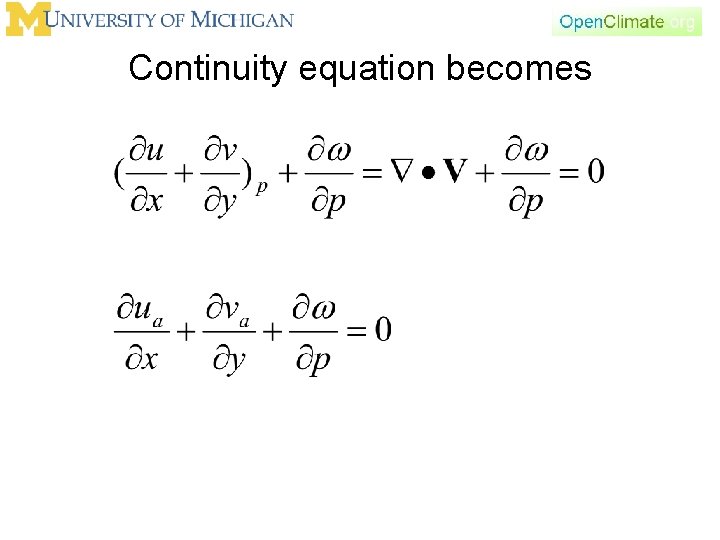
Continuity equation becomes

That’s easy • We did that on the test, in homework, so that makes a lot of sense. • Go on.

Thermodynamic equation static stability, Sp, is large; ω cannot be ignored geostrophic wind can be used here.

Thermodynamic equation (use the fact that atmosphere is near hydrostatic balance) Wait, wait … we neglected the vertical velocity up there in the momentum equation. I’d really like to neglect it here. Why can’t I? (Plus you’re just using the geostrophic wind again in the horizontal advection of temperature, and that practically tells me that this is no vertical wind. ) You’re right … What does that tell you about the vertical structure of the atmosphere?

Thermodynamic equation (use the fact that atmosphere is near hydrostatic balance) split temperature into basic state plus deviation

Thermodynamic equation (and with the hydrostatic equation) note the inverse relation of heating with pressure

Scaled equations of motion in pressure coordinates Definition of geostrophic wind Momentum equation Continuity equation Thermodynamic Energy equation

What is the point? • Set of equations that describes synopticscale motions and includes the effects of ageostrophic wind (vertical motion) • We do seem to have been rather capricious about when we used the geostrophic wind and when we didn’t, not to mention that whole thing about f and beta.

Scale Analysis = Make Assumptions Quasi-geostrophic system is good for: • Synoptic scales • Middle latitudes • Situations in which Va is important • Flows in approximate geostrophic and hydrostatic balance • Mid-latitude cyclones

Scale Analysis = Make Assumptions Quasi-geostrophic system is not good for: • Very small or very large scales • Flows with large vertical velocities • Situations in which Va ≈ Vg • Flows not in approximate geostrophic and hydrostatic balance • Thunderstorms/convection, boundary layer, tropics, etc…

Outline • Vorticity in Atmosphere Redux • In Class Problem • Scaling Equations in Pressure Coordinates – Quasi-geostrophic Equations • Quasi-geostrophic Vorticity Equations

Excited students now … • Professor, professor, can we derive a vorticity equation from this set of scaled equations? I mean ever since I learned about vorticity, everything has seemed clear and worthwhile. I bet that then we could REALLY learn something about the atmosphere.

• A measure of planetary vorticity compared to relative vorticity. • A measure of the importance of rotation • A measure of the relative scales of the geostrophic and ageostrophic winds

Forming the QG Equations 1. Assume the horizontal wind is approximately geostrophic 2. Scale the material derivative 3. Assume the north-south variation of the coriolis parameter is constant 4. Modify the continuity equation 5. Modify thermodynamic equation

Approximate (scaled) horizontal momentum equation This equation states that the time rate of change of the geostrophic wind is related to 1. the coriolis force due to the ageostrophic wind and 2. the part of the coriolis force due to the variability of the coriolis force with latitude and the geostrophic wind. Both of these terms are smaller than the geostrophic wind itself.

Scaled equations of motion in pressure coordinates Definition of geostrophic wind Momentum equation Continuity equation Thermodynamic Energy equation

Where are we going with this? • Want to describe the evolution of two key features of the atmosphere – Large-scale waves (how does the distribution of geopotential height change with time? ) – Midlatitude cyclones (development of low pressure systems in the lower troposphere) • Influence of vertical motion, temperature advection, mass conservation…

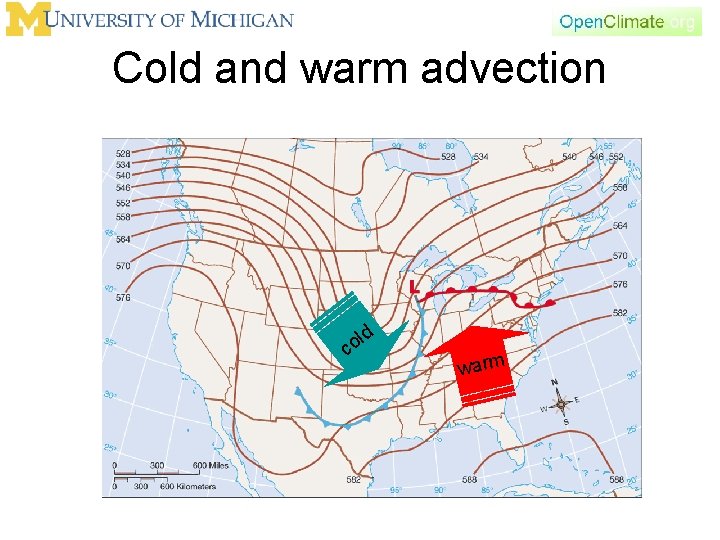
Cold and warm advection ld o c warm

What will we do next? • Derive a vorticity equation for these scaled equations. – Actually provides a “suitable” prognostic equation because will include div(ageostrophic wind). – Remember the importance of divergence in the vorticity equation…

Scaled horizontal momentum equations in pressure coordinates

Use definition of vorticity equation

Remember our scaled vorticity equation?

Remember our scaled vorticity equation? We see that the QG vorticity equation is very similar to the scaled vorticity equation we developed before …with a few additional assumptions

QG Vorticity Equation • So, now we have a vorticity equation… • How can we use this?

Where are we going with this? • Want to describe the evolution of two key features of the atmosphere – Large-scale waves (how does the distribution of geopotential height change with time? ) – Midlatitude cyclones (development of low pressure systems in the lower troposphere) • Influence of vertical motion, temperature advection, mass conservation…

Develop an equation for geopotential tendency Start with the QG vorticity equation Remember the definition of geostrophic wind? Plug this in, and we immediately have an equation for the time rate of change of the geopotential height!


In class problem: Thermal wind Refer to the figure. This figure shows a jet stream in the northern hemisphere, upper troposphere. The direction is easterly, from the east. We saw that in a hydrostatic atmosphere the vertical gradient of the geostrophic wind, was related to the horizontal gradient of temperature. That is thermal wind relationship. What is the sign of the vertical gradient of the wind below the jet stream? With this information, is point A warmer or colder than point B ? Where are the temperature gradients strongest ? Be sure to justify your decisions.

In class problem What is the sign of the vertical gradient of the wind below the jet stream? -30 m/s -10 m/s -20 m/s Between lower and upper point Δu is < 0, Δp < 0, hence vertical gradient is positive. A - p, vertical y, north -5 m/s B

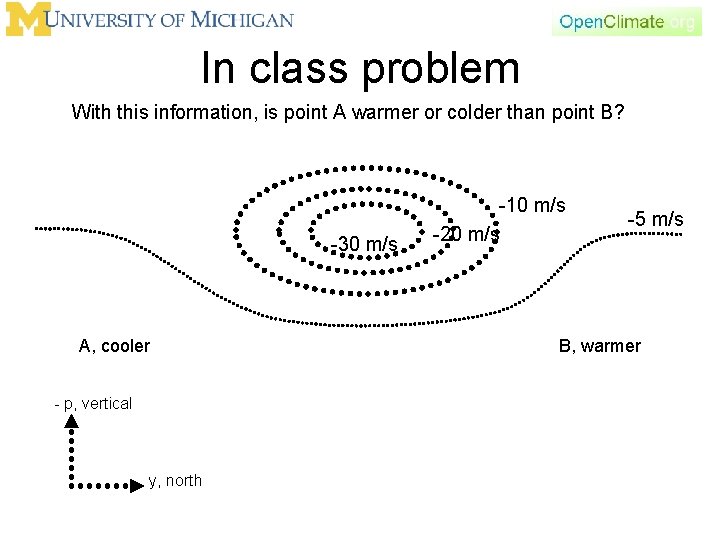
In class problem With this information, is point A warmer or colder than point B? -30 m/s A, cooler - p, vertical y, north -10 m/s -20 m/s -5 m/s B, warmer

In class problem (Pressure Coordinates) With this information, is point A warmer or colder than point B?

In class problem (Height Coordinates) With this information, is point A warmer or colder than point B?

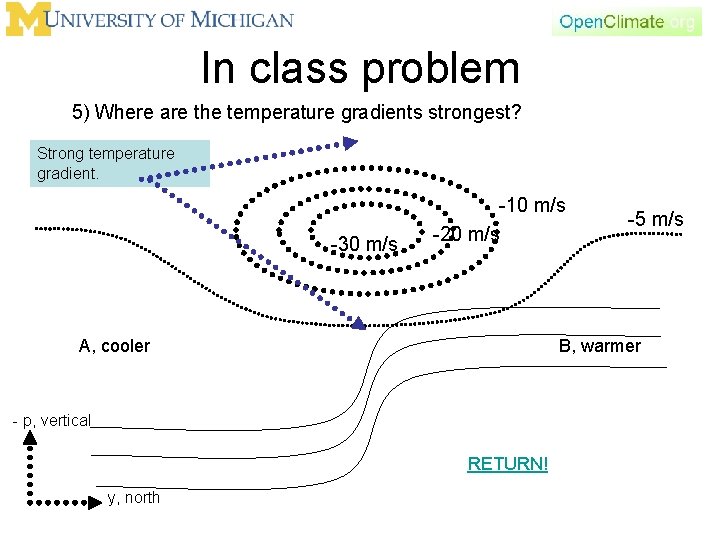
In class problem 5) Where are the temperature gradients strongest? Strong shear. -30 m/s A, cooler - p, vertical y, north -10 m/s -20 m/s -5 m/s B, warmer

In class problem 5) Where are the temperature gradients strongest? Strong temperature gradient. -30 m/s -10 m/s -20 m/s A, cooler B, warmer - p, vertical RETURN! y, north -5 m/s

In class problem: Perturbation a) Expand the material derivative using the definition of the velocity field given in the problem. b) Write an equation for the time rate of change (partial derivative in t) of the zonal mean velocity. (The partial in t for the perturbation velocity should not appear. )

In Class Problem: Solution (Return) Full equation Second term. . Full equation This is the zonal mean equation.

Weather • National Weather Service – Model forecasts: • Weather Underground – Model forecasts: • NCAR Research Applications Program