AOSS 401 Geophysical Fluid Dynamics Atmospheric Dynamics Prepared

AOSS 401 Geophysical Fluid Dynamics: Atmospheric Dynamics Prepared: 20131121 Quasi-geostrophic / Analysis / Weather Richard B. Rood (Room 2525, SRB) rbrood@umich. edu 734 -647 -3530 Cell: 301 -526 -8572

Class News • Ctools site (AOSS 401 001 F 13) • Second Examination on December 10, 2013 • Homework – Homework due November 26, 2013

Weather • National Weather Service – Model forecasts: • Weather Underground – Model forecasts: • NCAR Research Applications Program

So when you are through – You will know how to do scale analysis – You will know how to derive the vorticity equation – You will know the wave equation and how to seek “wave-like” solution – Something more about weather and climate

Some fundamental notions you will learn. • The importance of the conservation equation • Atmospheric motions organize in distinct spatial and temporal scales • Most of the dynamic disturbances of the atmosphere can be classified as either: – Waves – Vortices • There is a mean circulation of the atmosphere which is known as the general circulation. – What does this do? • The atmosphere has two dominate balances, at least away from the tropics: – Hydrostatic balance – Geostrophic balance • It is the deviations from this balance which we are most interested in.

Links for today • http: //www. wunderground. com/maps/ • http: //www. ecmwf. int/products/forecasts/d/ charts/medium/deterministic/msl_uv 850_z 500!Geopotential%20500%20 h. Pa%20 and %20 Temperature%20 at%20850%20 h. Pa!0 !North%20 hemisphere!pop!od!oper!public _plots!2013120500!!/ • http: //www. weatherforecast. com/maps/Arctic

Outline • Analysis of equations of atmospheric motion scaled for large-scale middle latitude dynamics / Quasi-geostrophic formalism – Review of large-scale formalism – Long and short waves / Barotropic waves – Examine ageostrophic wind – Cyclone development • Occlusion • Baroclinic Barotropic /// energy conversion • Vertical motion

Vorticity Equation DIVERGENCE TILTING SOLENOIDAL or BAROCLINIC Changes in relative vorticity are caused by: • Divergence • Tilting • Gradients in density on a pressure surface • Advection

QG Theory: Assumptions 1. Assume the horizontal wind is approximately geostrophic 2. Scale the material derivative • • Neglect the vertical advection Horizontal advection due to geostrophic wind 3. Assume the north-south variation of the coriolis parameter is constant 4. Divergence in the continuity equation only due to ageostrophic wind 5. Modify thermodynamic equation • • • Advection by the geostrophic wind Assume hydrostatic balance Vertical velocity acts on a mean static stability profile

The quasi-geostrophic (QG) equations momentum equation geostrophic wind continuity equation thermodynamic equation

Geopotential tendency equation Vorticity Advection Thickness Advection • Linear partial differential equation for geopotential tendency. • Given a geopotential distribution at an initial time, can compute geopotential distribution at a later time. • The right hand side is like a forcing.

First major set of conclusions from the quasi-geostrophic system We see that – Geostrophic advection of geostrophic vorticity causes waves to propagate – The vertical difference in temperature (thickness) advection causes waves to amplify

Remember our scaled vorticity equation? We see that the QG vorticity equation is very similar to the scaled vorticity equation we developed before …with a few additional assumptions

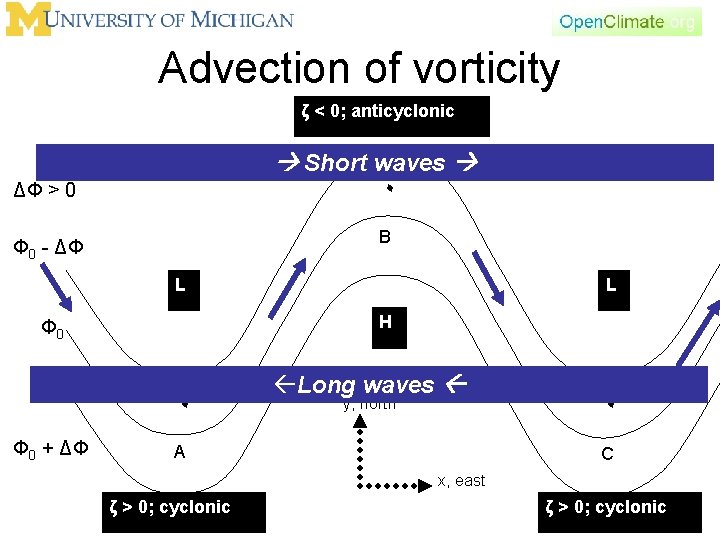
Long and Short Waves • In this discussion these are both “largescale” meaning that rotation is important. • Therefore, this is a “short” large-scale wave versus a “long” large-scale wave.

Barotropic Wave Dispersion • Look at the barotropic wave equation

Consider a barotropic fluid Think here

Assume a “wave like solution” (get used to this…) Dispersion relation. Relates frequency and wave number to flow. Must be true for waves.

Stationary wave? Wind must be positive, from the west, for a wave.

Consider a more specific form of a wave solution

Assume that the geopotential takes the form of a wave Mean Wave Mean Ф Gradient in y Horizontal wavenumber

Remember the relationship between geostrophic wind and geopotential Plug in the wave solution for the geopotential height

Divide the geostrophic wind into mean and perturbation Divide wind into mean and perturbation, assume no mean north/south wind Perturbation only mean perturbation

Plug into the advection of relative vorticity

Plug into the advection of planetary vorticity

Compare advection of planetary and relative vorticity

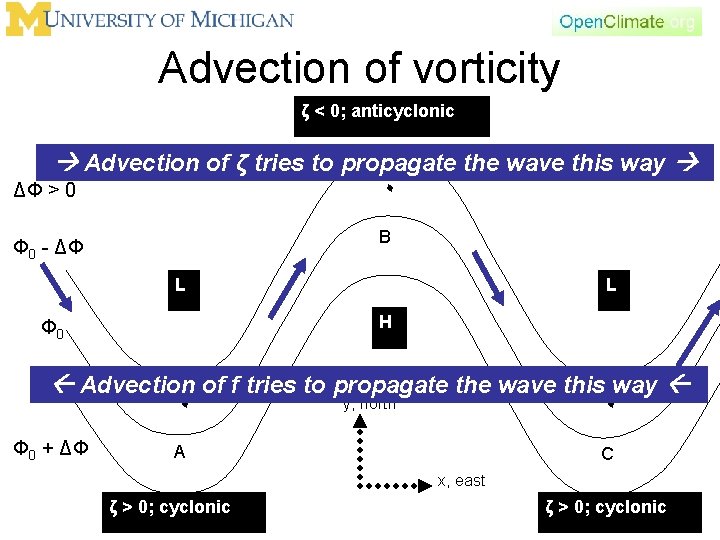
Advection of vorticity ζ < 0; anticyclonic Advection of ζ tries to propagate the wave this way ٠ ΔΦ > 0 B Φ 0 - ΔΦ L L H Φ 0 Advection of f tries to propagate the wave this way ٠ Φ 0 + ΔΦ ٠ y, north A C x, east ζ > 0; cyclonic

Advection of vorticity ζ < 0; anticyclonic Short waves ٠ ΔΦ > 0 B Φ 0 - ΔΦ L H Φ 0 ٠ Φ 0 + ΔΦ L ßLong waves y, north A ٠ C x, east ζ > 0; cyclonic

More about the ageostrophic wind • Review ageostrophic wind and implications for vertical motion and cyclone development • Use all that we know to describe development of a mid-latitude cyclone

A closer look at the ageostrophic wind • Start with our momentum equation • Just for kicks, take • and see what happens

A closer look at the ageostrophic wind • Now, by the right hand rule: • and remember • so we can write

A closer look at the ageostrophic wind • We end up with • …the ageostrophic wind! • Knowing that the divergence of the ageostrophic wind leads to vertical motion, let’s explore the implications of this…

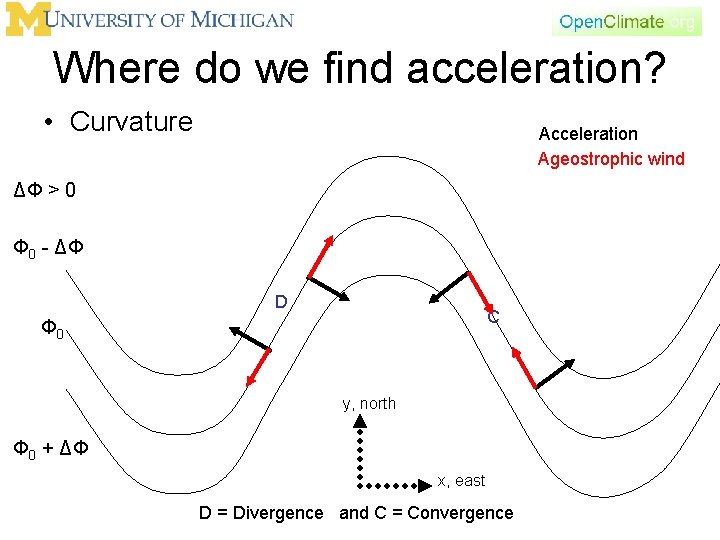
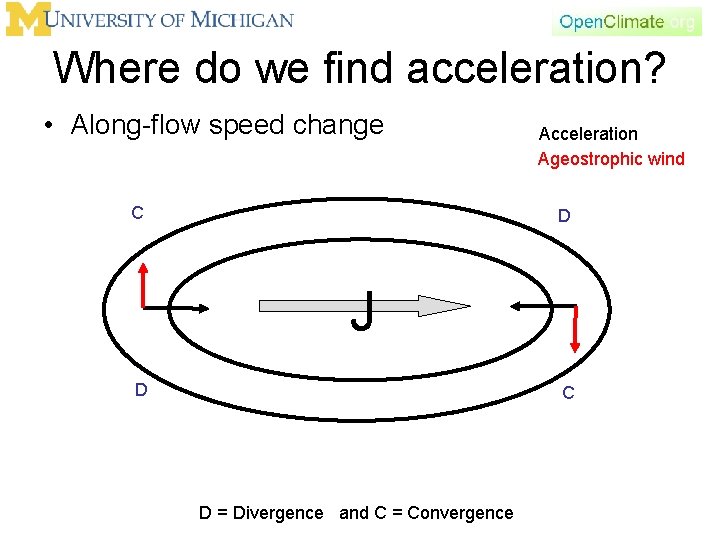
Where do we find acceleration? • Curvature Acceleration Ageostrophic wind ΔΦ > 0 Φ 0 - ΔΦ D C Φ 0 y, north Φ 0 + ΔΦ x, east D = Divergence and C = Convergence

Where do we find acceleration? • Along-flow speed change

Where do we find acceleration? • Along-flow speed change C Acceleration Ageostrophic wind D J D C D = Divergence and C = Convergence

Where do we find acceleration? • Along-flow speed change

Vorticity at upper and lower levels • Continue to examine the divergence of the wind Which is a proxy for the vertical velocity

One more application… • Start with the identity • Now, consider the divergence of the ageostrophic wind • Use the identity, and we have

What is this? • Formally, this is • Which is how we derived the vorticity equation

What can we do with this? • Plug in our QG assumptions • Let’s think about the difference in divergence (of the ageostrophic wind) between two levels – By the continuity equation, this means that mass is either increasing in the column (net convergence) or decreasing in the column (net divergence) – This should tell us whether low pressure or high pressure is developing at the surface…

Column Net Convergence/Divergence • Subtract vorticity equation at 1000 h. Pa from vorticity equation at 500 h. Pa • Gives us the net divergence between 1000 and 500 h. Pa • It can be shown that

Examine each term • “Steering term” • Low-level centers of vorticity propagate in the direction of thermal wind • (Along the gradient of thickness)

Examine each term • “Development term” • A bit complicated • Remember, thermal wind is the vertical change in the geostrophic wind • This term indicates the influence of a tilt with height of the location of the maximum (minimum) in vorticity • Fundamentally: if the location of the maximum in vorticity shifts westward with height, the low will develop.

Development term Combine terms Definition of thermal wind Definition of geostrophic vorticity

Development term • Remember the barotropic height tendency equation? • How about the omega equation?

Development term • Development term is the vertical change in barotropic advection of vorticity • This is the same as the stretching term in the omega equation • If the upper-level wave propagates faster than the surface wave, the system decays • Otherwise, the system may develop…

Implications • Surface low and high pressure systems (centers of maximum/minimum vorticity) propagate along lines of constant thickness • If there is a vertical tilt westward with height of the vorticity, then a surface low pressure system can intensify (increase in low-level positive vorticity)

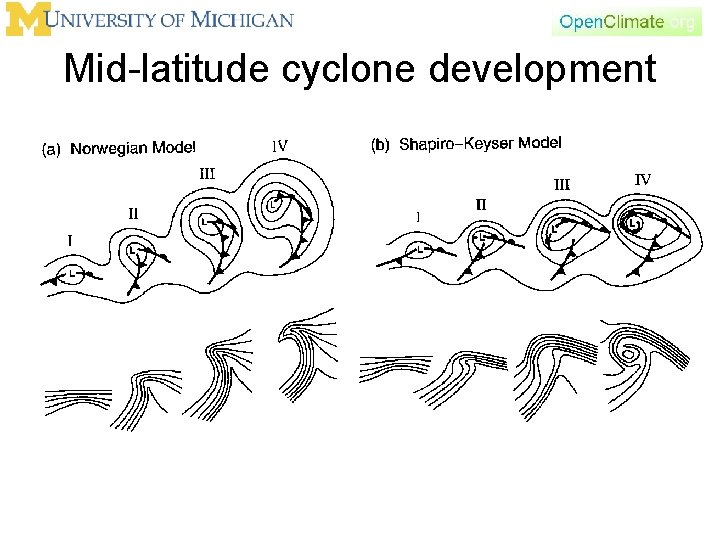
Look at Cyclones

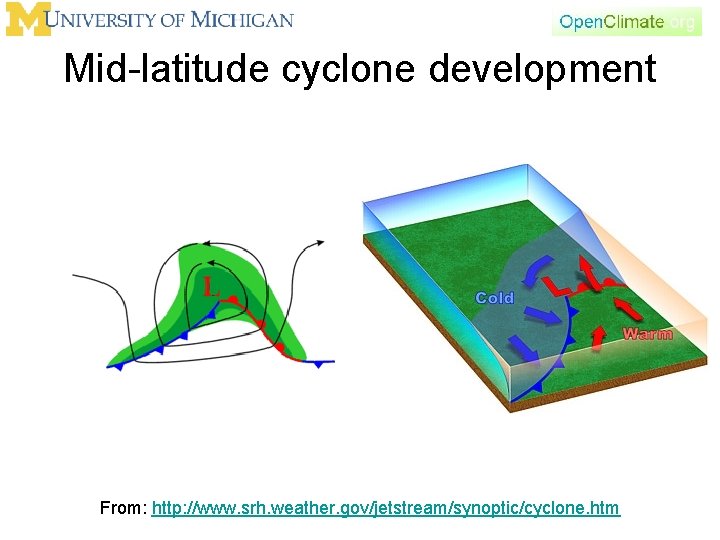
Mid-latitude cyclone development

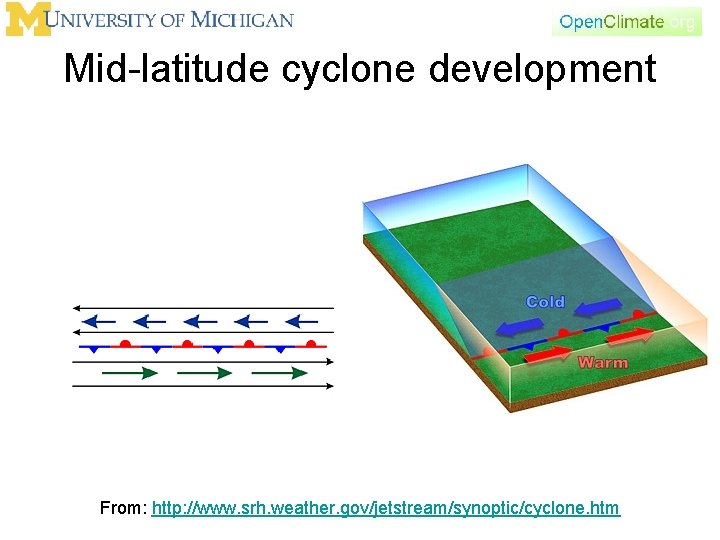
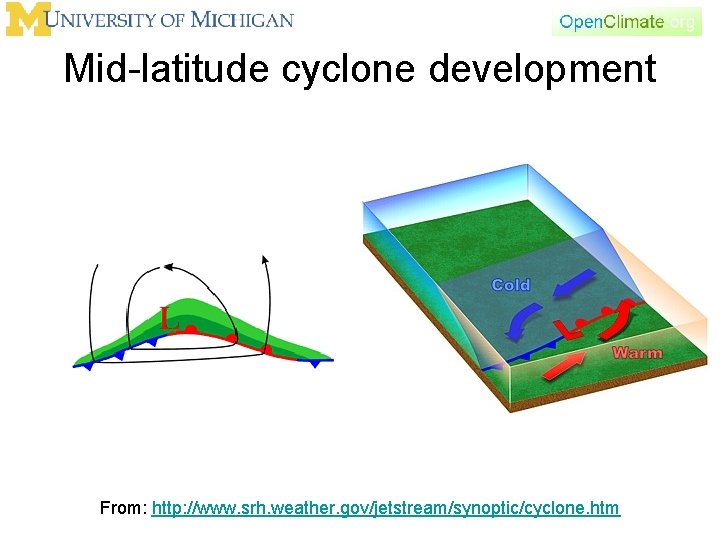
Mid-latitude cyclone development From: http: //www. srh. weather. gov/jetstream/synoptic/cyclone. htm

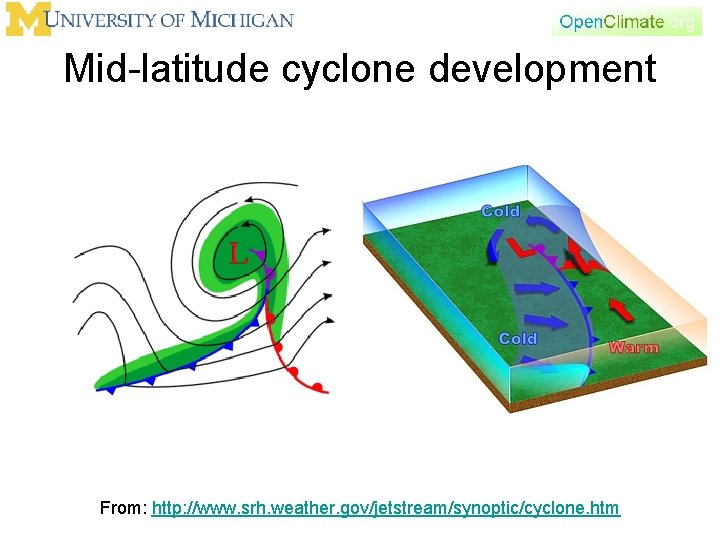
Mid-latitude cyclone development From: http: //www. srh. weather. gov/jetstream/synoptic/cyclone. htm

Mid-latitude cyclone development From: http: //www. srh. weather. gov/jetstream/synoptic/cyclone. htm

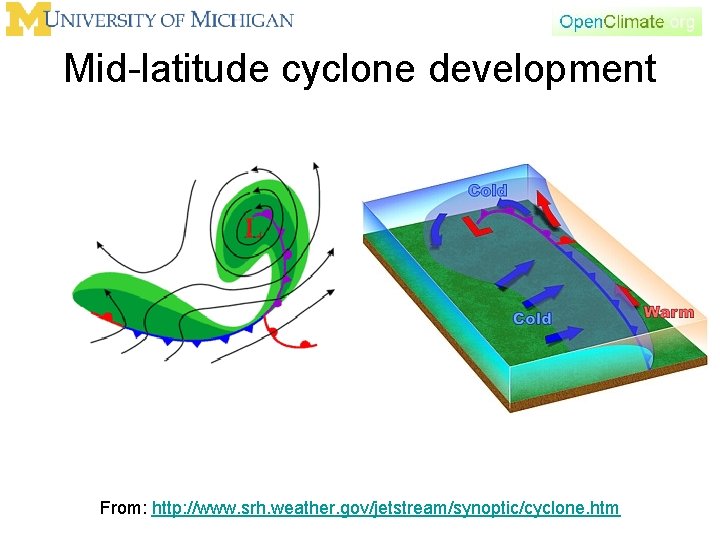
Mid-latitude cyclone development From: http: //www. srh. weather. gov/jetstream/synoptic/cyclone. htm

Mid-latitude cyclone development From: http: //www. srh. weather. gov/jetstream/synoptic/cyclone. htm

In the classic cyclone model • Occlusion describes the transition of a cyclone from baroclinic (west-ward tilt with height) to barotropic (“vertically stacked”) • Once there is no more westward vertical tilt with height, no further development can occur

Baroclinic Barotropic

Idealized Development of a Baroclinic Wave • Start with a N-S temperature gradient and associated wind speed maximum in the upper troposphere • Introduce a low-level perturbation • Watch the conversion of PE to KE and the development of the wave…

Energetics of Midlatitude Cyclone Development • The jet stream is commonly associated with strong temperature gradients in the middle/lower troposphere (thermal wind relationship) • Mid-latitude cyclones develop along waves in the jet stream • By thermal wind balance, this means that mid-latitude cyclones develop along strong horizontal temperature gradients (fronts) • There is a link between the strength of the horizontal temperature gradient and cyclone development…

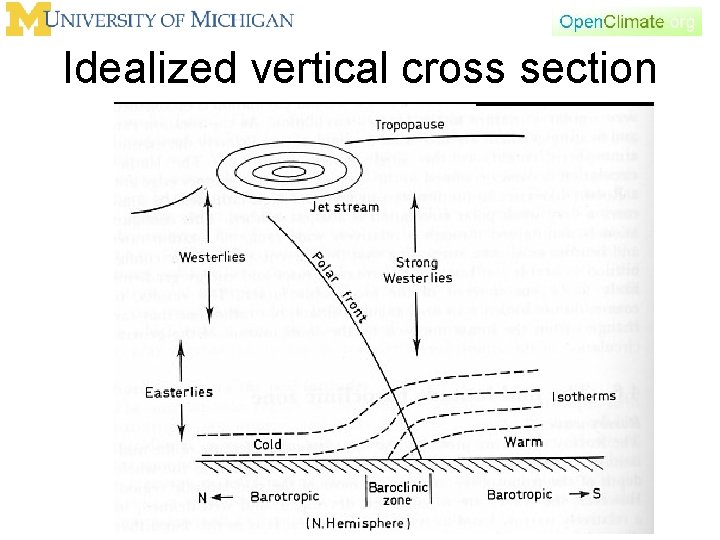
Idealized vertical cross section

Two important definitions • barotropic – density depends only on pressure. – By the ideal gas equation, surfaces of constant pressure are surfaces of constant density are surfaces of constant temperature (idealized assumption). = (p) • baroclinic – density depends on pressure and temperature (as in the real world). = (p, T)

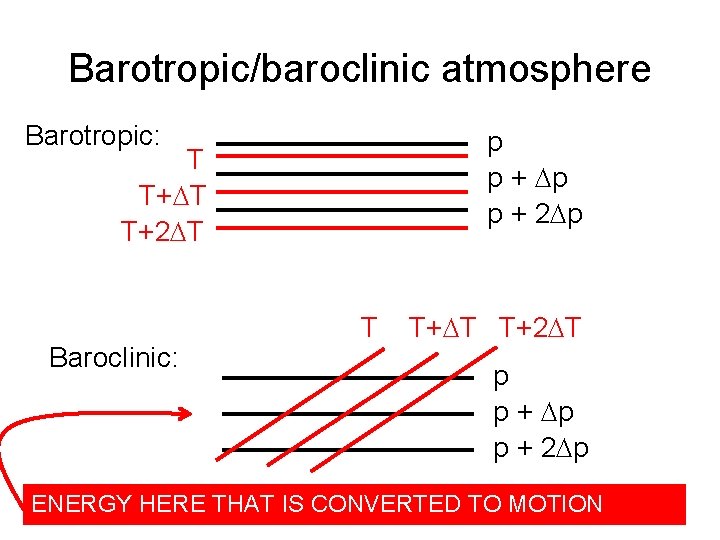
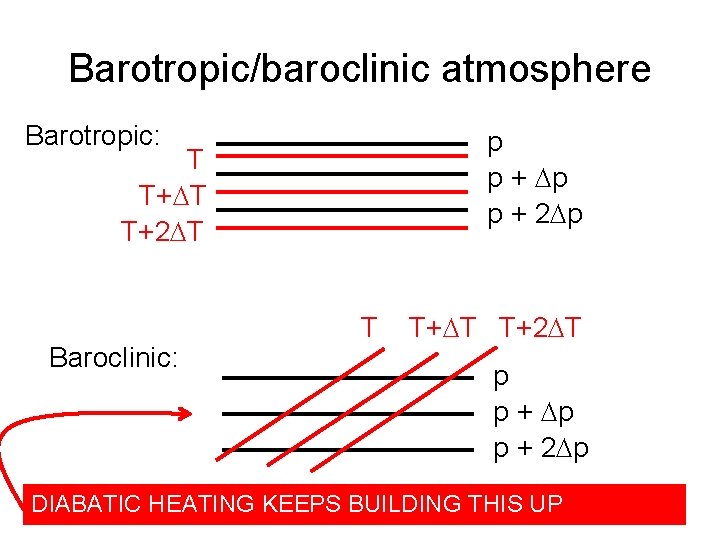
Barotropic/baroclinic atmosphere Barotropic: p p + 2 p T T+2 T Baroclinic: T T+2 T p p + 2 p ENERGY HERE THAT IS CONVERTED TO MOTION

Barotropic/baroclinic atmosphere Barotropic: p p + 2 p T T+2 T Baroclinic: T T+2 T p p + 2 p DIABATIC HEATING KEEPS BUILDING THIS UP

Barotropic/baroclinic atmosphere • Energetics: – Baroclinic = temperature contrast = density contrast = available potential energy – Extratropical cyclones intensify through conversion of available potential energy to kinetic energy

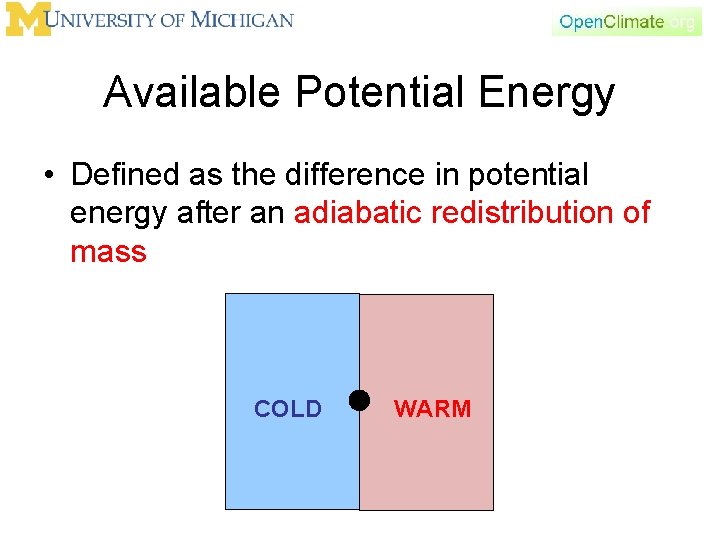
Available Potential Energy • Defined as the difference in potential energy after an adiabatic redistribution of mass COLD WARM

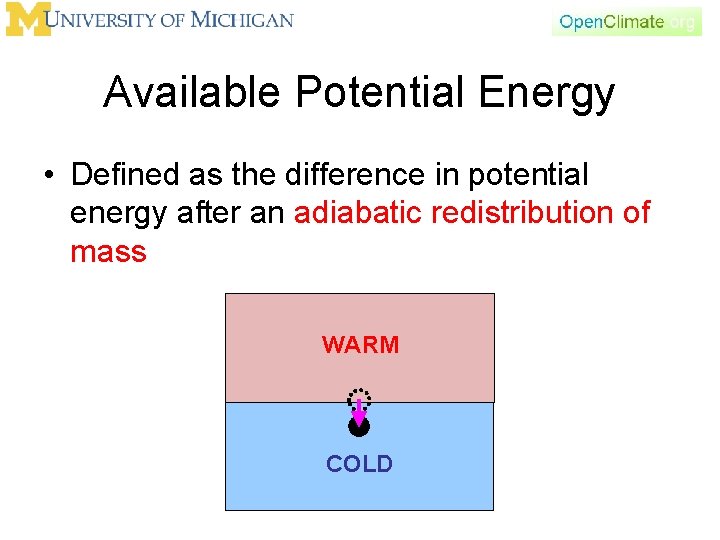
Available Potential Energy • Defined as the difference in potential energy after an adiabatic redistribution of mass WARM COLD

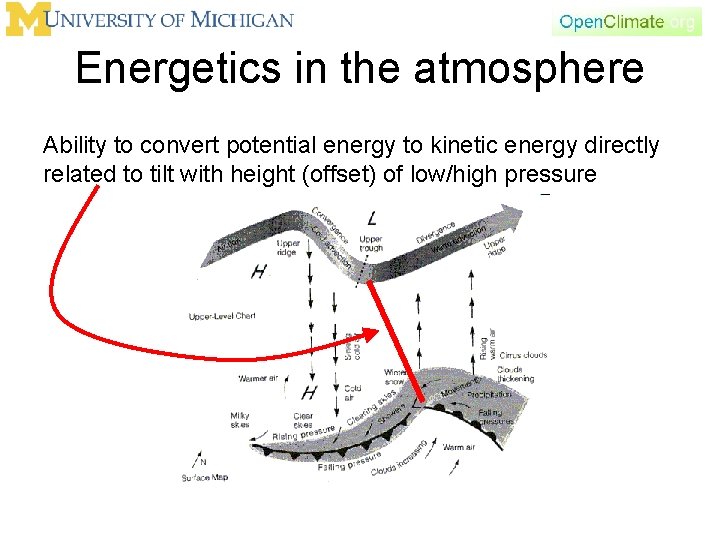
Energetics in the atmosphere • Diabatic heating (primarily radiation) maintains the equator to pole temperature contrast • Strength of temperature contrast referred to as “baroclinicity” • Cyclones at mid-latitudes reduce this temperature contrast—adjust baroclinic atmosphere toward barotropic

Energetics in the atmosphere Ability to convert potential energy to kinetic energy directly related to tilt with height (offset) of low/high pressure

Energetics in the atmosphere • Diabatic heating (primarily radiation) maintains the equator to pole temperature contrast • Strength of temperature contrast referred to as “baroclinicity” • Cyclones at mid-latitudes reduce this temperature contrast—adjust baroclinic atmosphere toward barotropic • We can quantify this, but first let’s go back to the ageostrophic wind…

Baroclinic Barotropic Transition

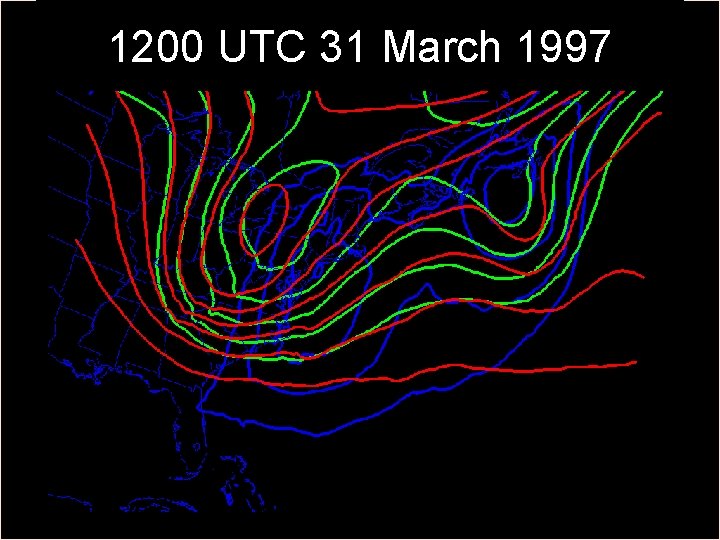
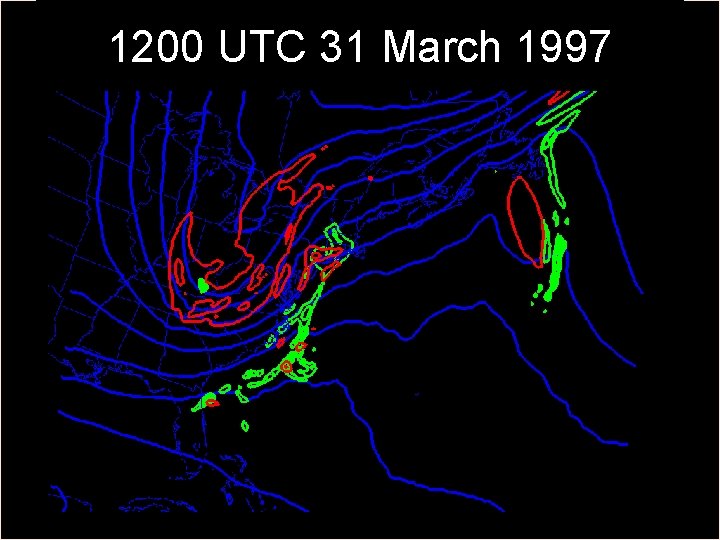
1200 UTC 31 March 1997

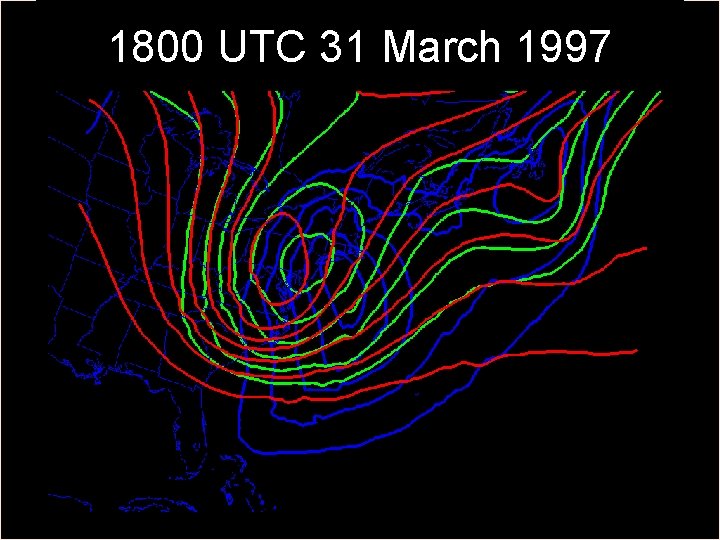
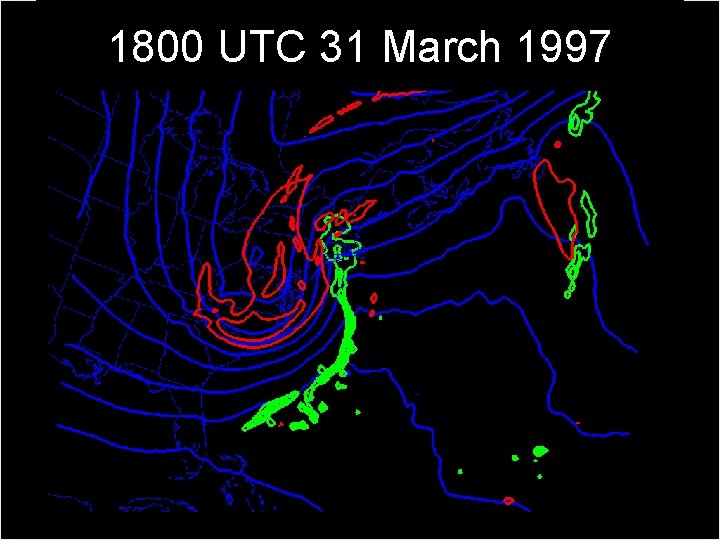
1800 UTC 31 March 1997

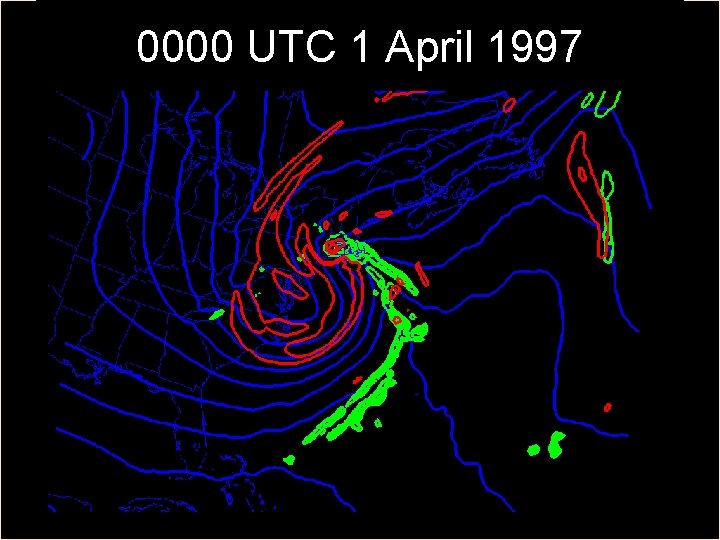
0000 UTC 1 April 1997

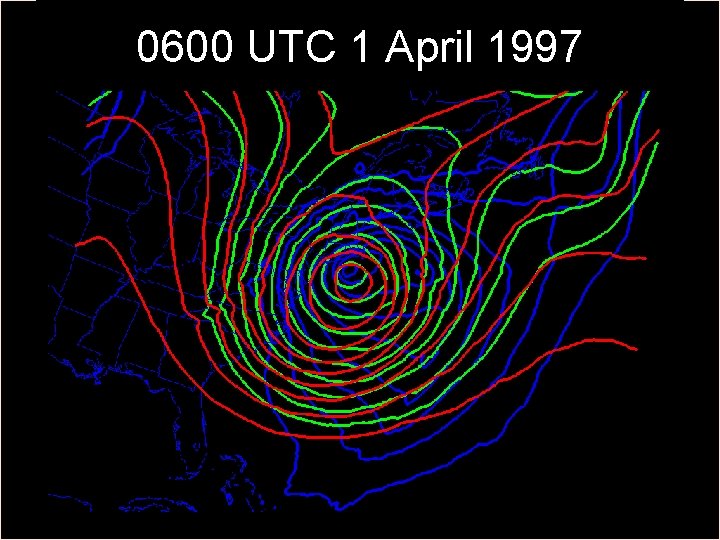
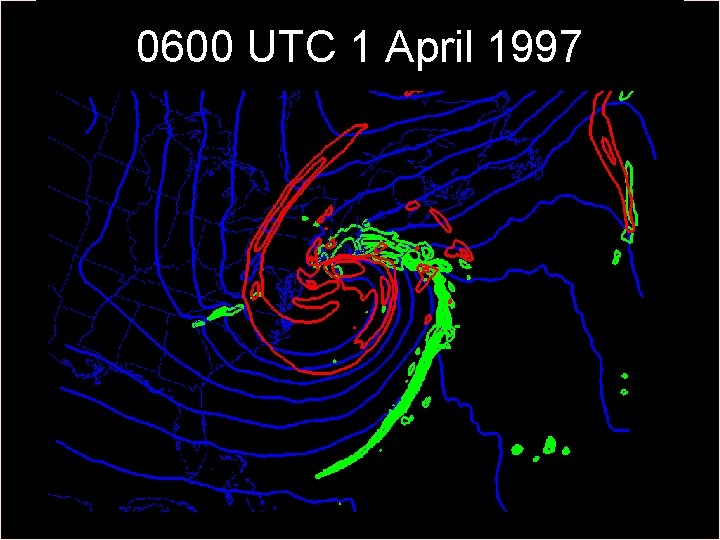
0600 UTC 1 April 1997

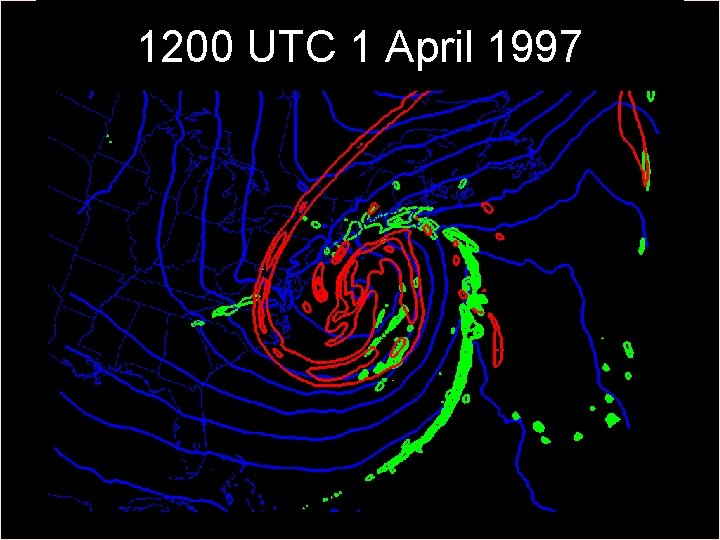
1200 UTC 1 April 1997

Vertical velocity: Omega equation • • Kinematic method Horizontal advection Diabatic method Omega equation

Characteristics of large-scale vertical velocity • In all of the estimates for vertical velocity what is missing? – The answer is ________ • The vertical velocity in this large-scale, mid -latitude description of dynamics is exactly what is needed to maintain what balances ______ ?

QG-omega equation Combine all QG equations • Link between vertical derivative of vorticity advection (divergence/stretching) and vertical motion

QG-omega equation Combine all QG equations • Link between vertical derivative of vorticity advection (divergence/stretching) and vertical motion • Link between temperature advection and vertical motion

QG-omega equation Combine all QG equations • Link between vertical derivative of vorticity advection (divergence/stretching) and vertical motion • Link between temperature advection and vertical motion • Link between diabatic heating and vertical motion

QG-omega equation (simplified) Advection of absolute vorticity by thermal wind

“Advection” by thermal wind? • How to analyze this on a map? s es f to en kn di ic ra Th G la cu di en to rp Pe is al m er d Th Win r Look at contours of constant thickness

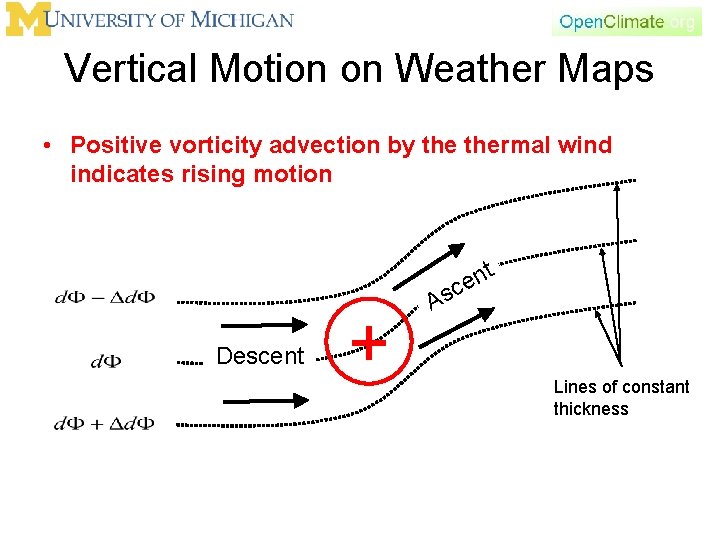
Vertical Motion on Weather Maps • Laplacian of omega is proportional to -ω • Omega can be analyzed as: • Remember, from definition of omega and scale analysis • Positive vorticity advection by thermal wind indicates rising motion

Vertical Motion on Weather Maps • Positive vorticity advection by thermal wind indicates rising motion t Descent + n e c s A Lines of constant thickness

Omega Equation

1200 UTC 31 March 1997

1800 UTC 31 March 1997

0000 UTC 1 April 1997

0600 UTC 1 April 1997

1200 UTC 1 April 1997

Take Away Messages • Large-scale dynamics / quasi-geostrophic theory – Hydrostatic balance – Geostrophic balance • Vertical motion is important, but above balances are always maintained – Vertical motion is diagnosed / no time dependence (though it changes with time) • Vertical motion is linked to divergence of horizontal wind ageostrophic wind • Vertical motion works against static stability, which is large. This is how baroclinicity is represented in the equations, despite baroclinic terms being scaled out • We have looked at dynamics of large-scale waves in different ways heuristically, theoretically and on maps. We see consistency and different insights. The mathematics proves a way to both quantify and explore the behavior of the dynamics.