AO DE LAS CUMBRES MUNDIALES EN EL PERU

“AÑO DE LAS CUMBRES MUNDIALES EN EL PERU” UNIVERSIDAD NACIONAL DE EDUCACIÓN “ENRIQUE GUZMÁN Y VALLE”- LA CANTUTA ESCUELA DE POST GRADO: SEMINARIO I MATEMATICA RECREATIVA 1

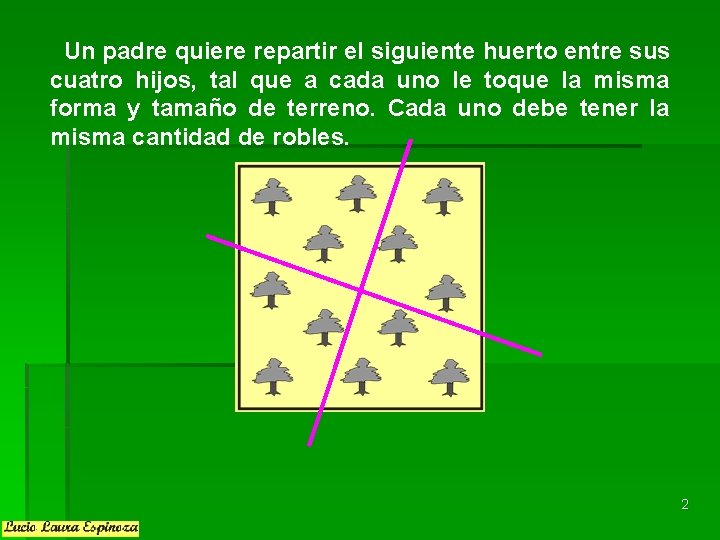
Un padre quiere repartir el siguiente huerto entre sus cuatro hijos, tal que a cada uno le toque la misma forma y tamaño de terreno. Cada uno debe tener la misma cantidad de robles. 2

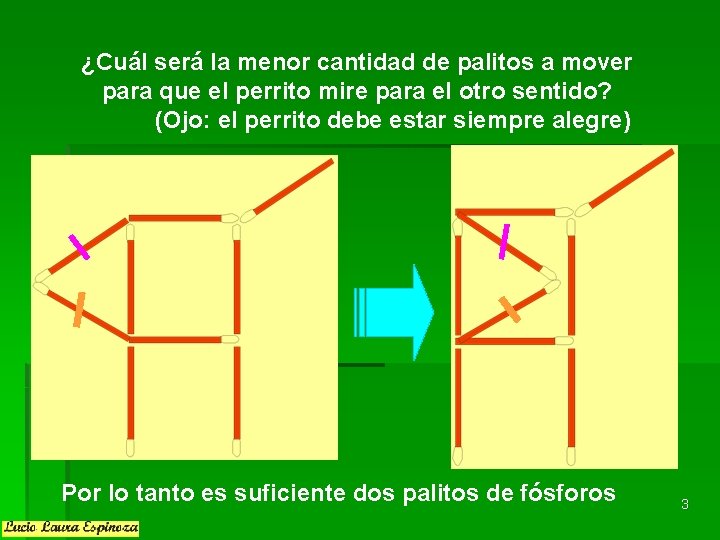
¿Cuál será la menor cantidad de palitos a mover para que el perrito mire para el otro sentido? (Ojo: el perrito debe estar siempre alegre) Por lo tanto es suficiente dos palitos de fósforos 3

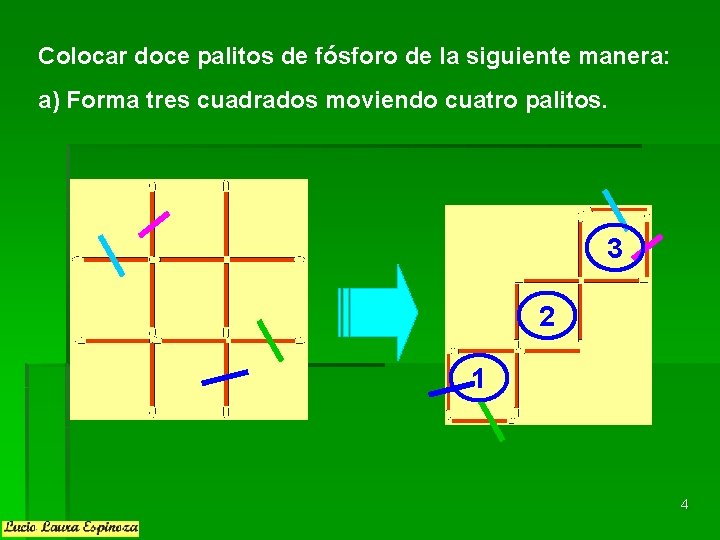
Colocar doce palitos de fósforo de la siguiente manera: a) Forma tres cuadrados moviendo cuatro palitos. 3 2 1 4

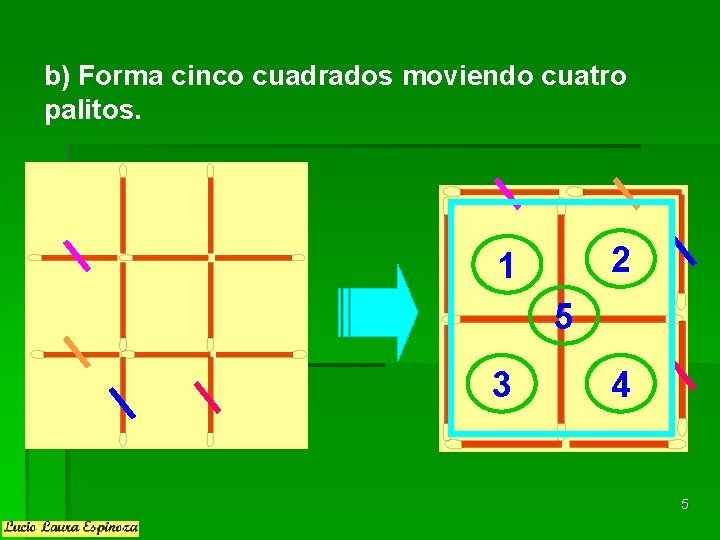
b) Forma cinco cuadrados moviendo cuatro palitos. 2 1 5 3 4 5

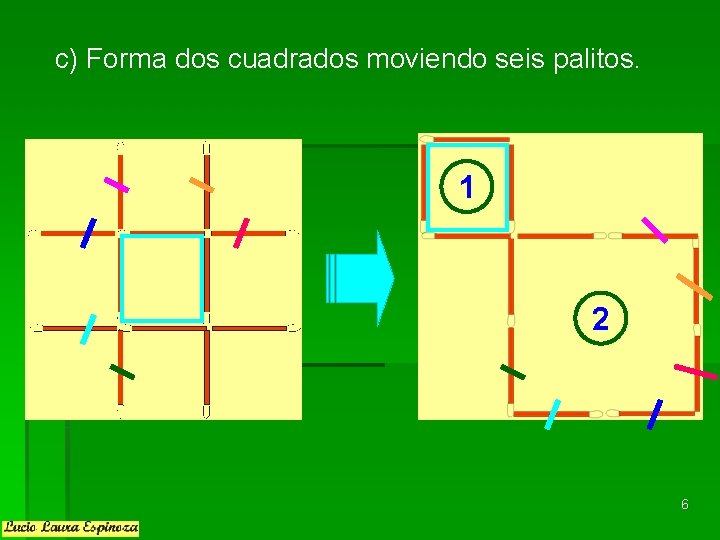
c) Forma dos cuadrados moviendo seis palitos. 1 2 6

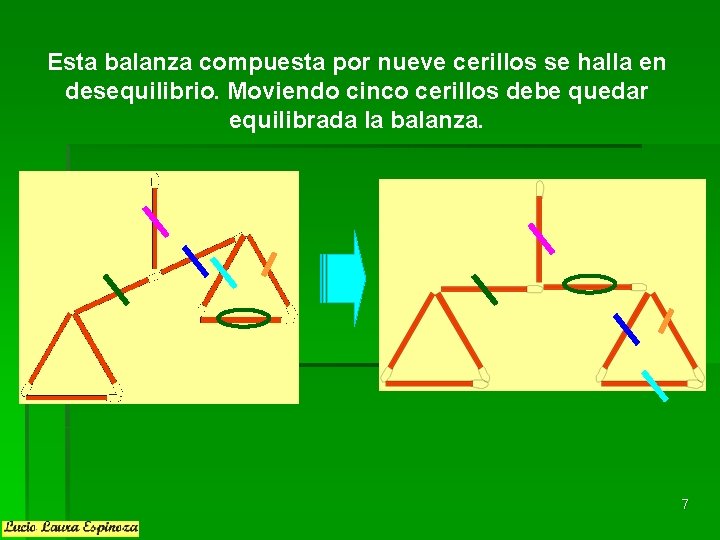
Esta balanza compuesta por nueve cerillos se halla en desequilibrio. Moviendo cinco cerillos debe quedar equilibrada la balanza. 7

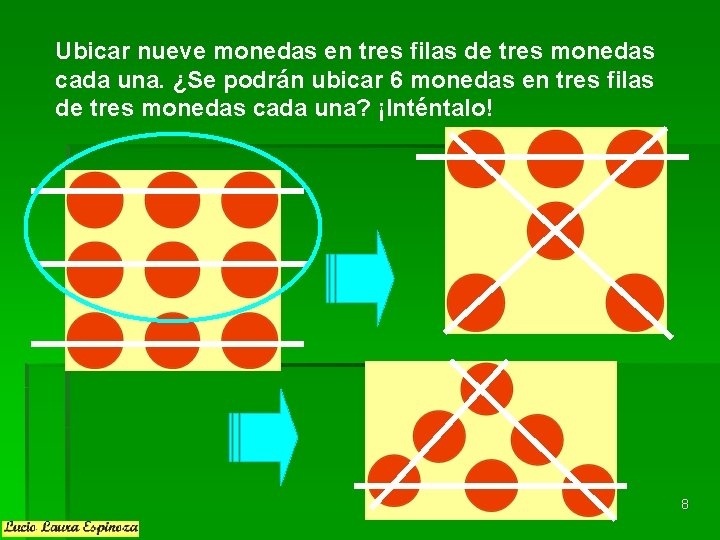
Ubicar nueve monedas en tres filas de tres monedas cada una. ¿Se podrán ubicar 6 monedas en tres filas de tres monedas cada una? ¡Inténtalo! 8

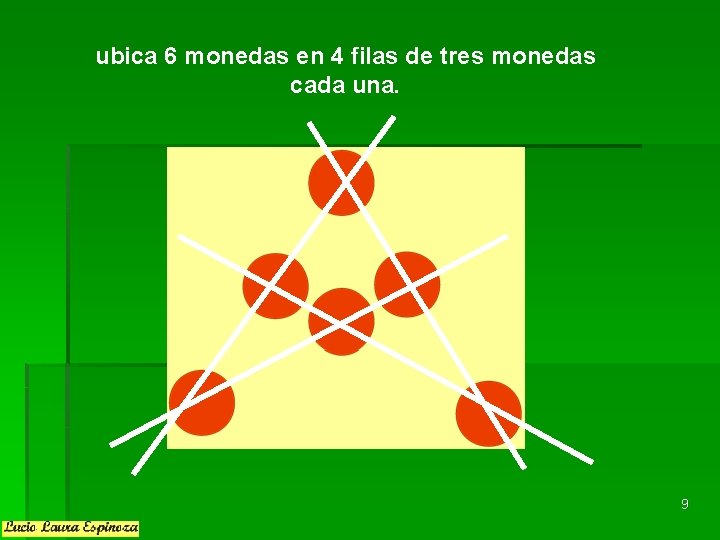
ubica 6 monedas en 4 filas de tres monedas cada una. 9

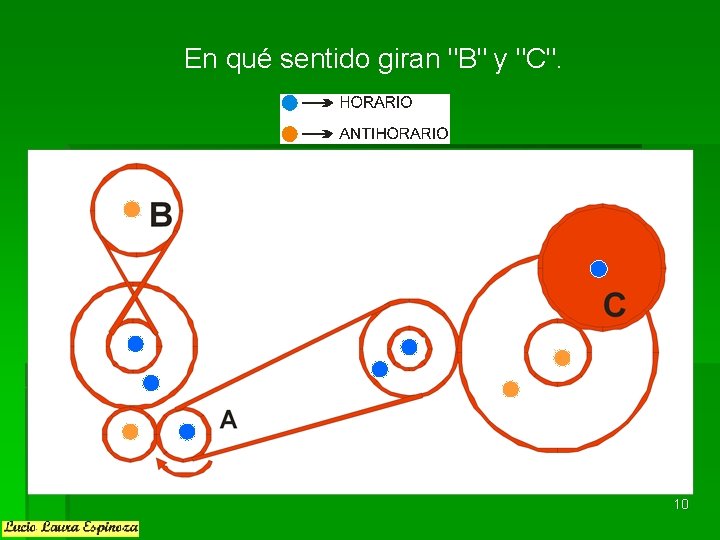
En qué sentido giran "B" y "C". 10

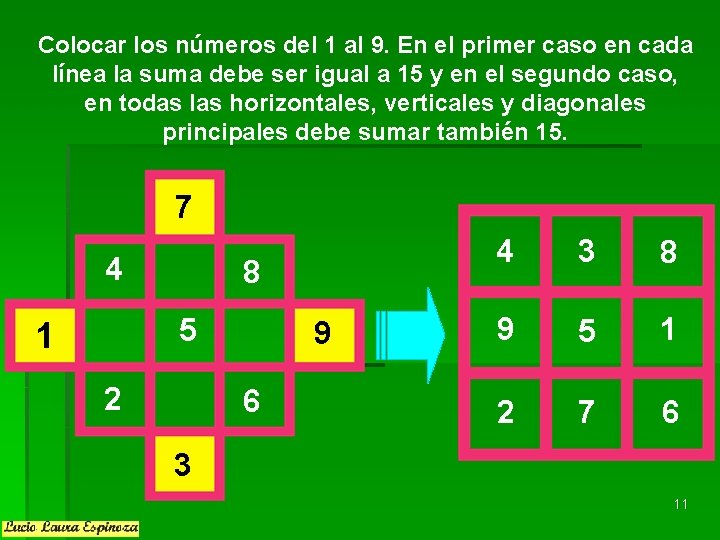
Colocar los números del 1 al 9. En el primer caso en cada línea la suma debe ser igual a 15 y en el segundo caso, en todas las horizontales, verticales y diagonales principales debe sumar también 15. 7 4 8 5 1 2 9 6 4 3 8 9 5 1 2 7 6 3 11

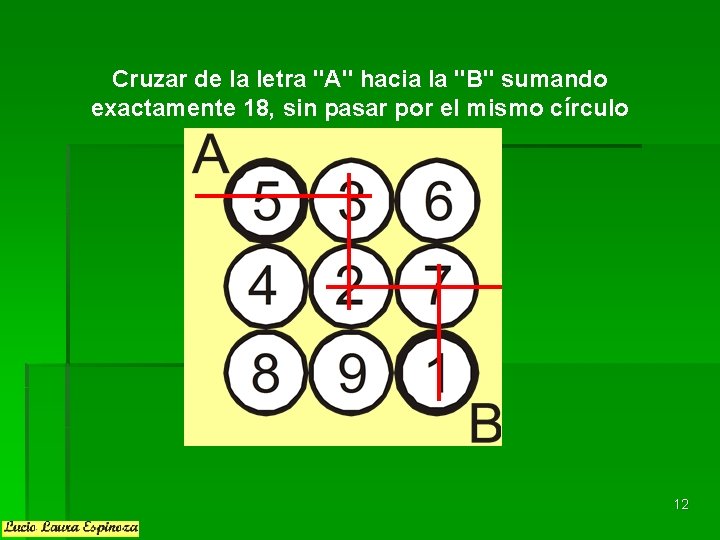
Cruzar de la letra "A" hacia la "B" sumando exactamente 18, sin pasar por el mismo círculo 12

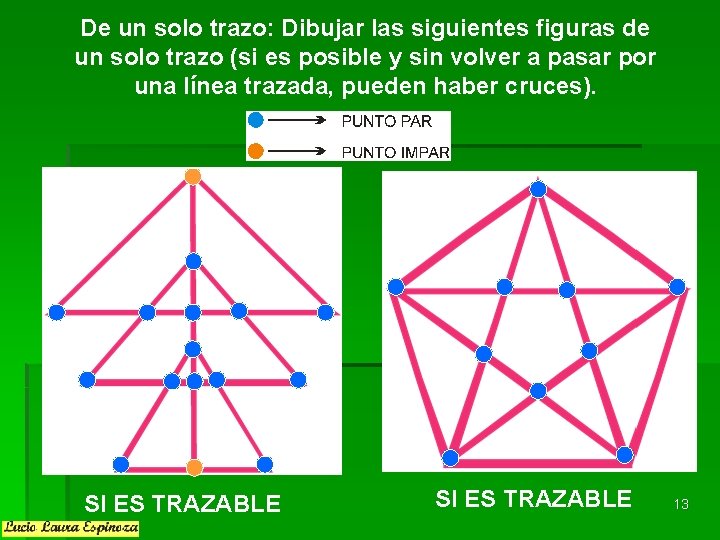
De un solo trazo: Dibujar las siguientes figuras de un solo trazo (si es posible y sin volver a pasar por una línea trazada, pueden haber cruces). SI ES TRAZABLE 13

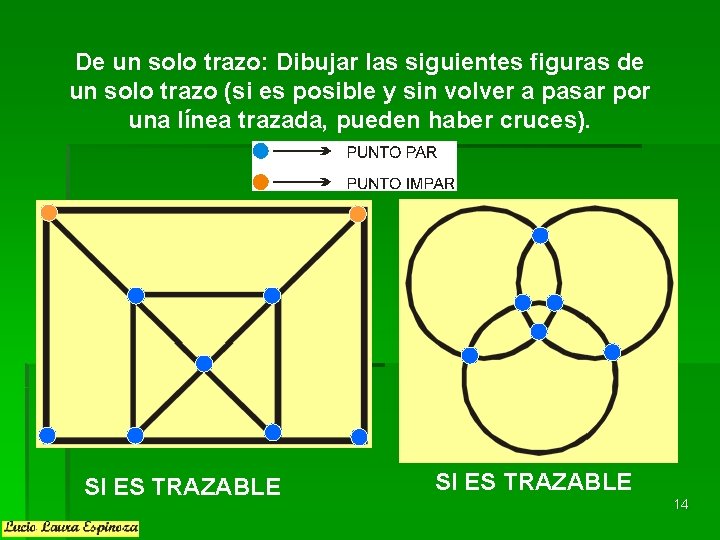
De un solo trazo: Dibujar las siguientes figuras de un solo trazo (si es posible y sin volver a pasar por una línea trazada, pueden haber cruces). SI ES TRAZABLE 14

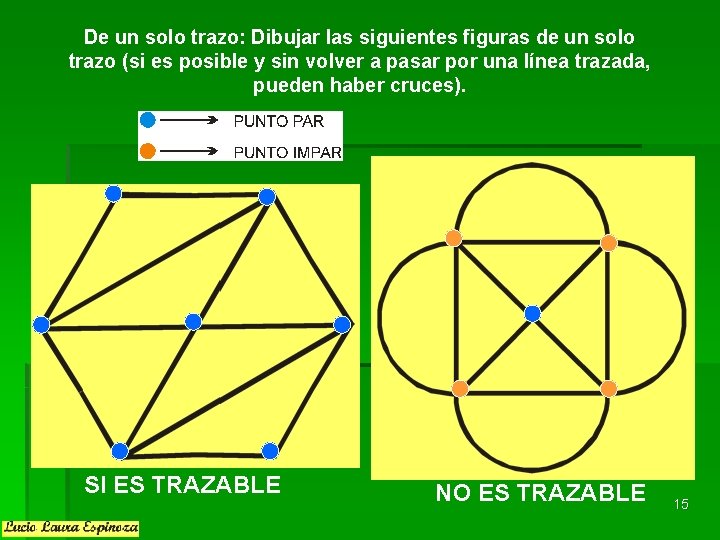
De un solo trazo: Dibujar las siguientes figuras de un solo trazo (si es posible y sin volver a pasar por una línea trazada, pueden haber cruces). SI ES TRAZABLE NO ES TRAZABLE 15

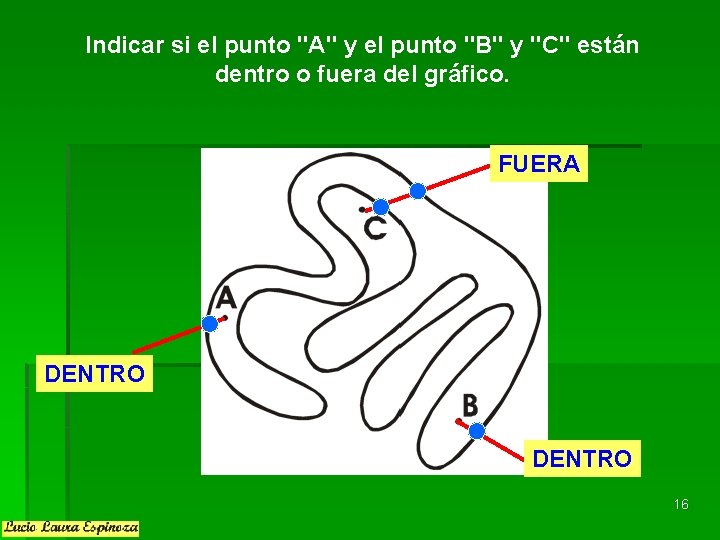
Indicar si el punto "A" y el punto "B" y "C" están dentro o fuera del gráfico. FUERA DENTRO 16

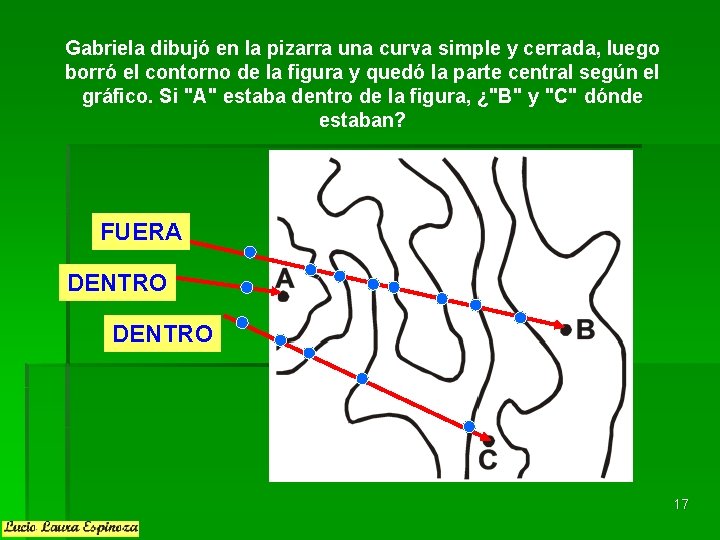
Gabriela dibujó en la pizarra una curva simple y cerrada, luego borró el contorno de la figura y quedó la parte central según el gráfico. Si "A" estaba dentro de la figura, ¿"B" y "C" dónde estaban? FUERA DENTRO 17

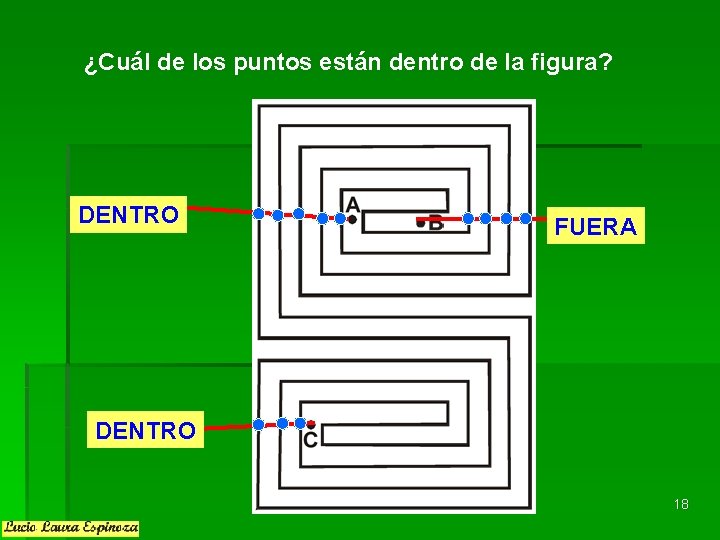
¿Cuál de los puntos están dentro de la figura? DENTRO FUERA DENTRO 18

Distribuir los ocho dígitos siguientes de manera que formen un número en el cual los "1" estén separados por un dígito, los "2" por dos dígitos, los "3" por tres dígitos y los "4" por cuatro dígitos. 11223344 4 1 3 1 2 4 3 2 19

Cuántas parejas de cifras (sólo en forma horizontal) suman 11. (un minuto). 20

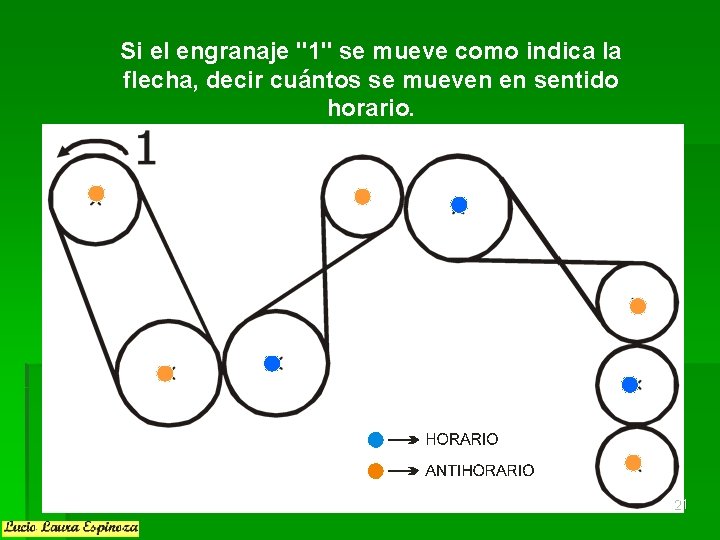
Si el engranaje "1" se mueve como indica la flecha, decir cuántos se mueven en sentido horario. 21

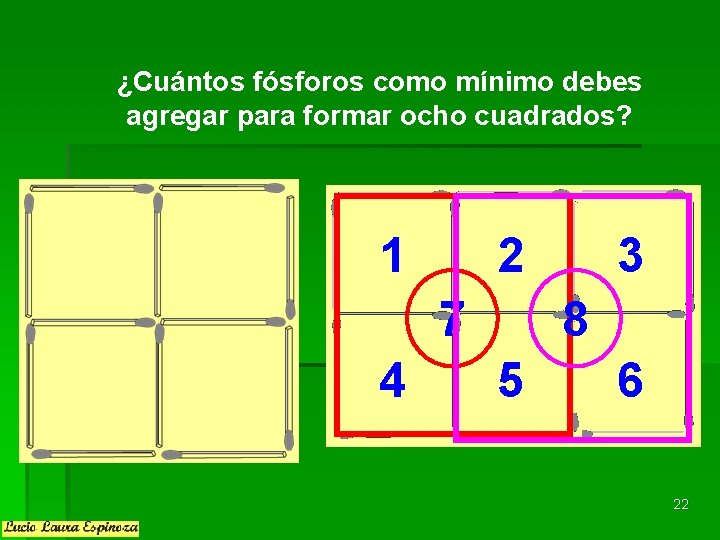
¿Cuántos fósforos como mínimo debes agregar para formar ocho cuadrados? 1 2 7 4 3 8 5 6 22

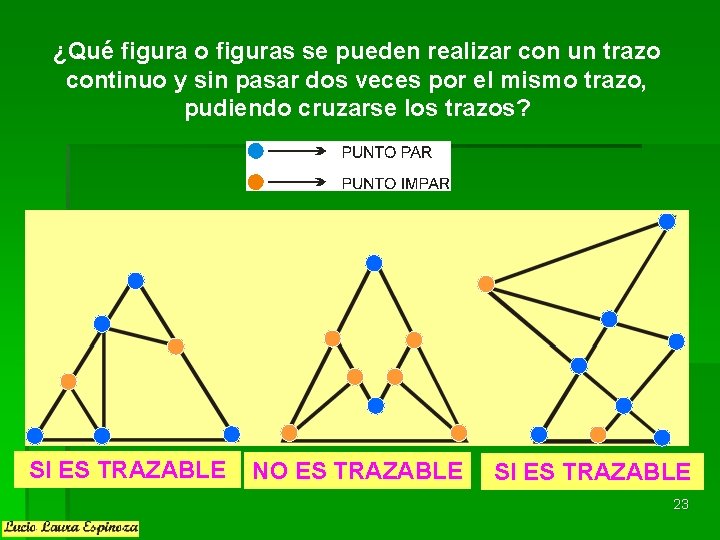
¿Qué figura o figuras se pueden realizar con un trazo continuo y sin pasar dos veces por el mismo trazo, pudiendo cruzarse los trazos? SI ES TRAZABLE NO ES TRAZABLE SI ES TRAZABLE 23

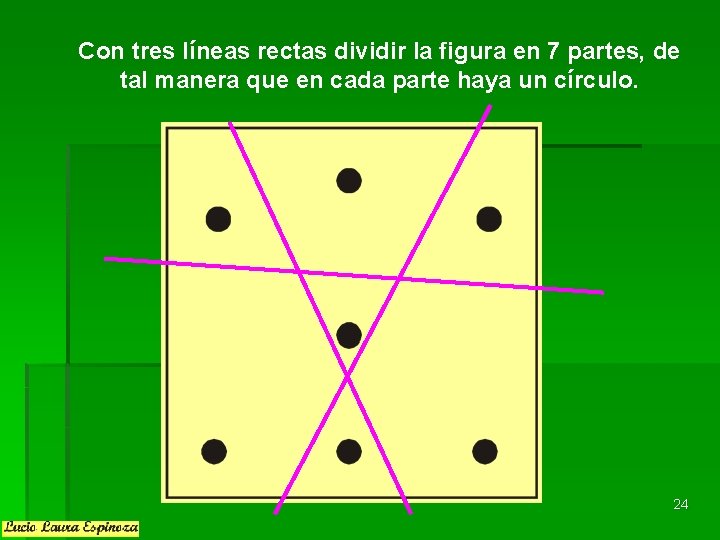
Con tres líneas rectas dividir la figura en 7 partes, de tal manera que en cada parte haya un círculo. 24

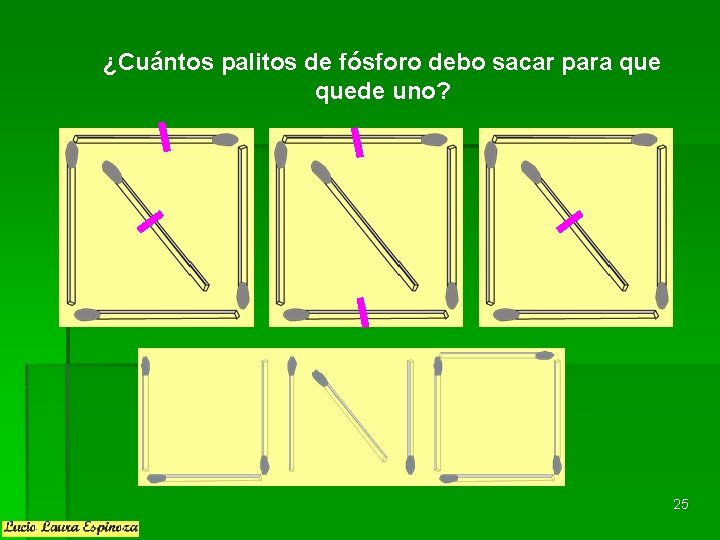
¿Cuántos palitos de fósforo debo sacar para quede uno? 25

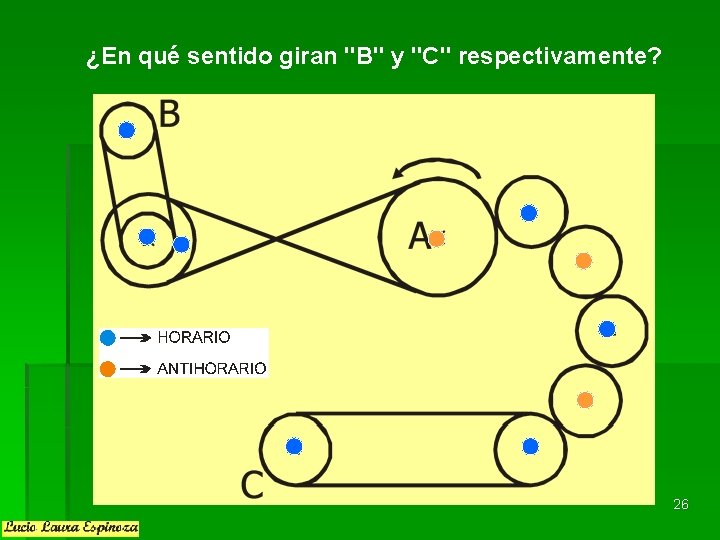
¿En qué sentido giran "B" y "C" respectivamente? 26

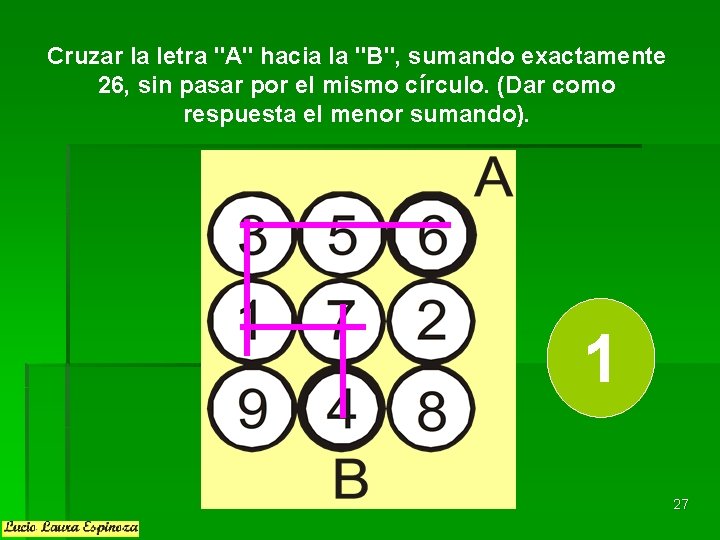
Cruzar la letra "A" hacia la "B", sumando exactamente 26, sin pasar por el mismo círculo. (Dar como respuesta el menor sumando). 1 27

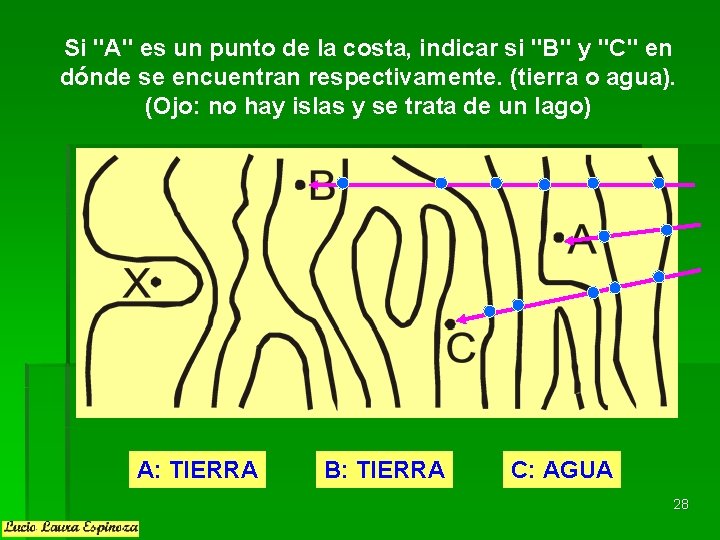
Si "A" es un punto de la costa, indicar si "B" y "C" en dónde se encuentran respectivamente. (tierra o agua). (Ojo: no hay islas y se trata de un lago) A: TIERRA B: TIERRA C: AGUA 28

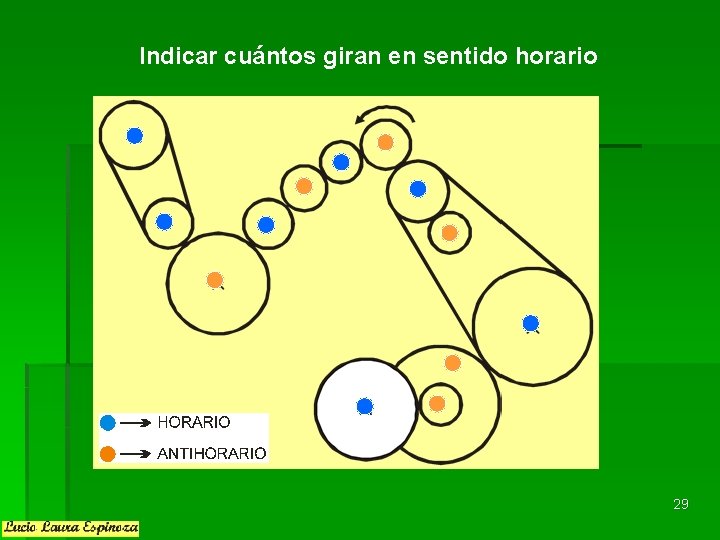
Indicar cuántos giran en sentido horario 29

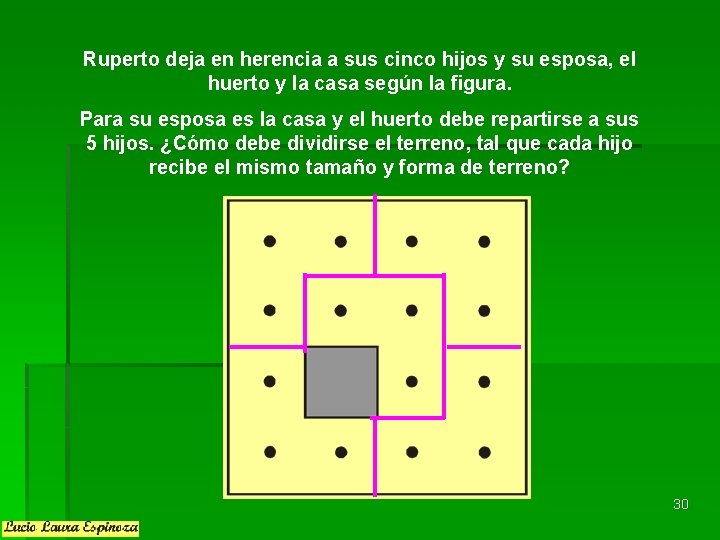
Ruperto deja en herencia a sus cinco hijos y su esposa, el huerto y la casa según la figura. Para su esposa es la casa y el huerto debe repartirse a sus 5 hijos. ¿Cómo debe dividirse el terreno, tal que cada hijo recibe el mismo tamaño y forma de terreno? 30

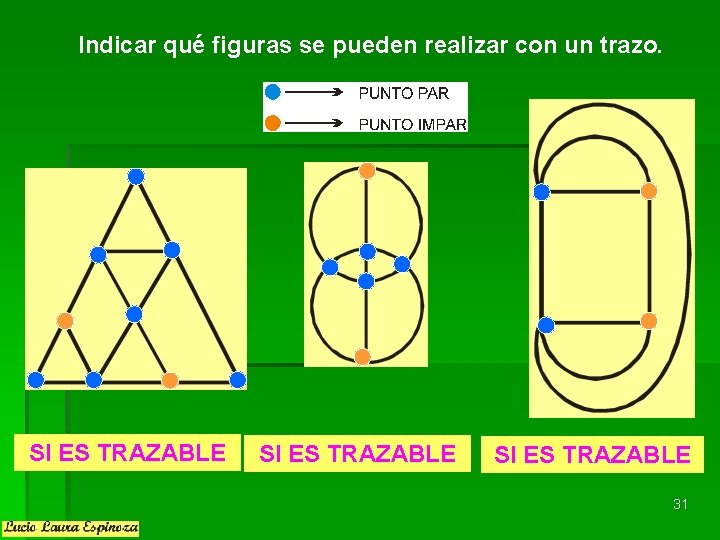
Indicar qué figuras se pueden realizar con un trazo. SI ES TRAZABLE 31

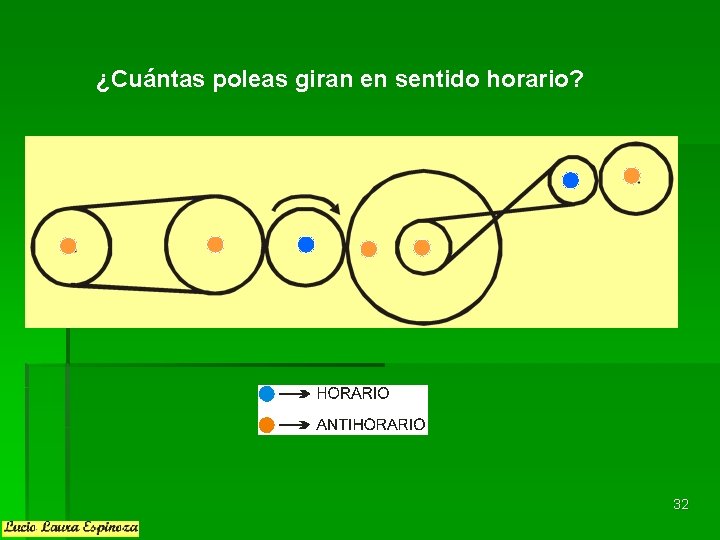
¿Cuántas poleas giran en sentido horario? 32

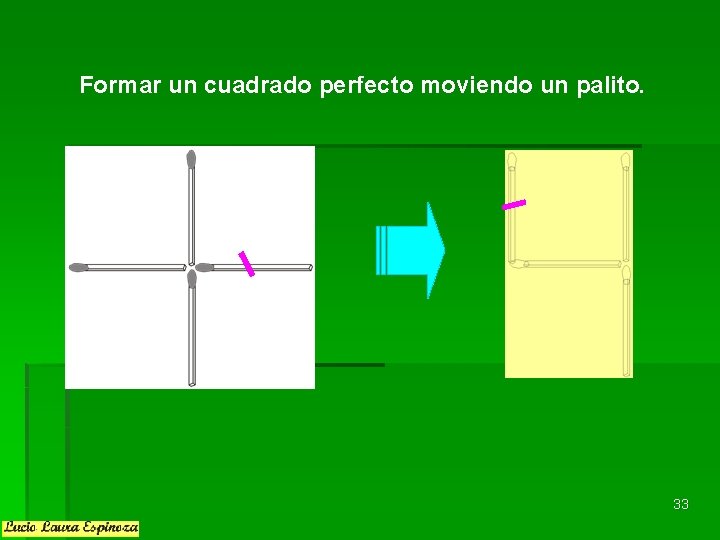
Formar un cuadrado perfecto moviendo un palito. 33

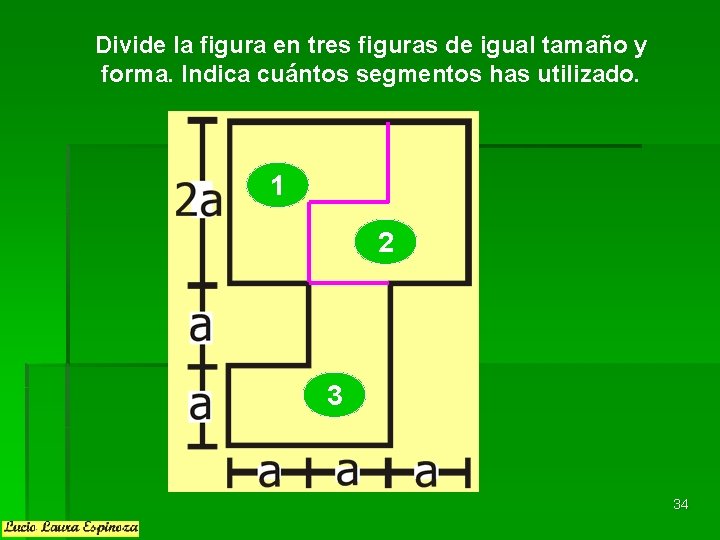
Divide la figura en tres figuras de igual tamaño y forma. Indica cuántos segmentos has utilizado. 1 2 3 34

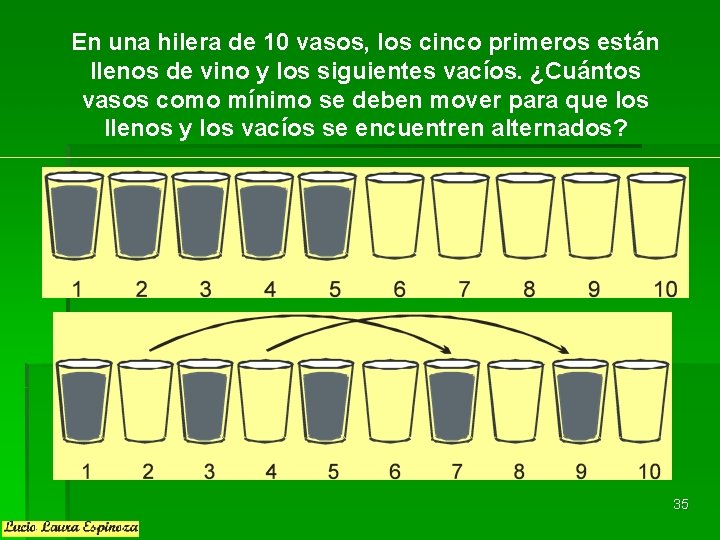
En una hilera de 10 vasos, los cinco primeros están llenos de vino y los siguientes vacíos. ¿Cuántos vasos como mínimo se deben mover para que los llenos y los vacíos se encuentren alternados? 35

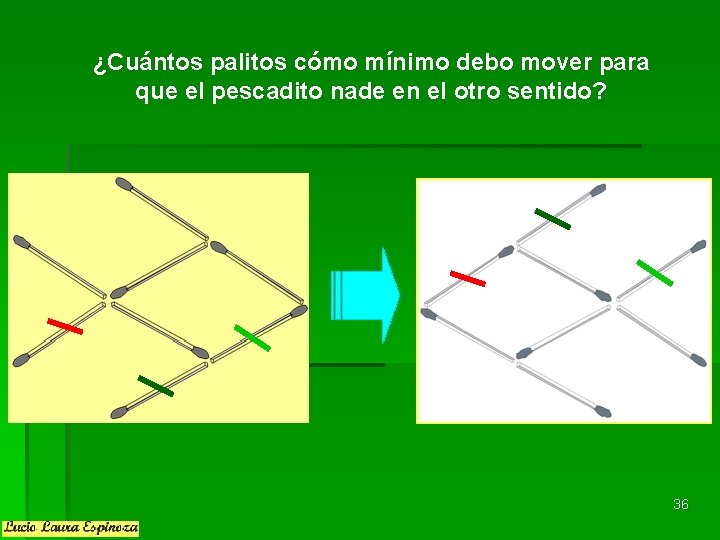
¿Cuántos palitos cómo mínimo debo mover para que el pescadito nade en el otro sentido? 36

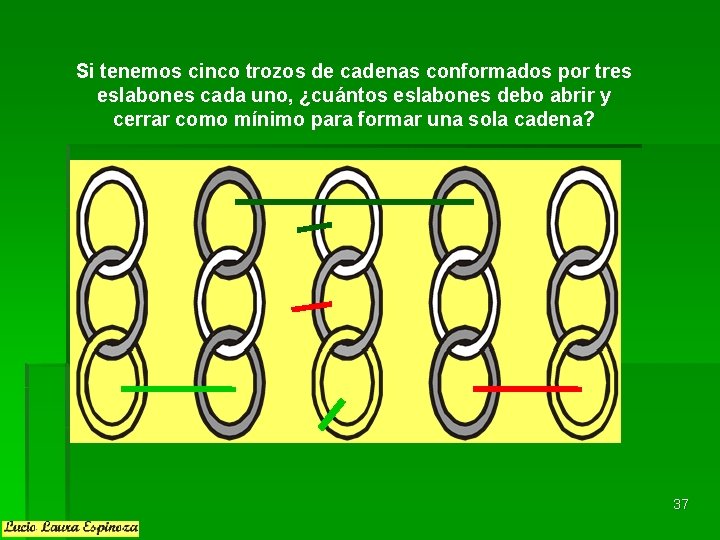
Si tenemos cinco trozos de cadenas conformados por tres eslabones cada uno, ¿cuántos eslabones debo abrir y cerrar como mínimo para formar una sola cadena? 37

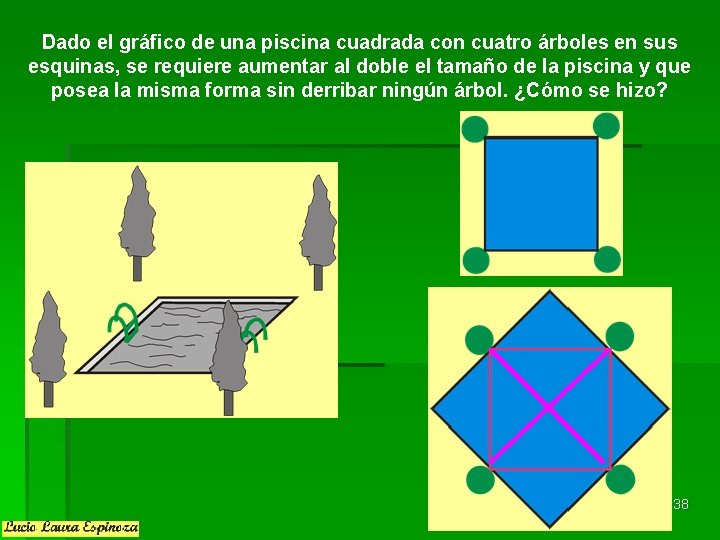
Dado el gráfico de una piscina cuadrada con cuatro árboles en sus esquinas, se requiere aumentar al doble el tamaño de la piscina y que posea la misma forma sin derribar ningún árbol. ¿Cómo se hizo? 38

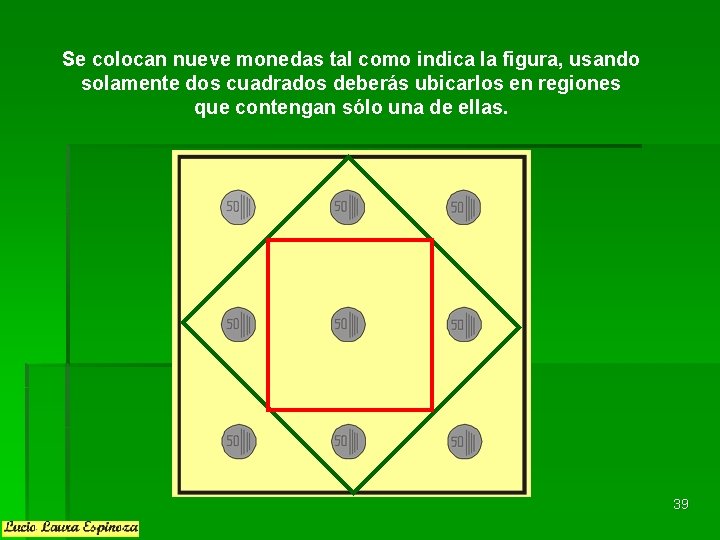
Se colocan nueve monedas tal como indica la figura, usando solamente dos cuadrados deberás ubicarlos en regiones que contengan sólo una de ellas. 39

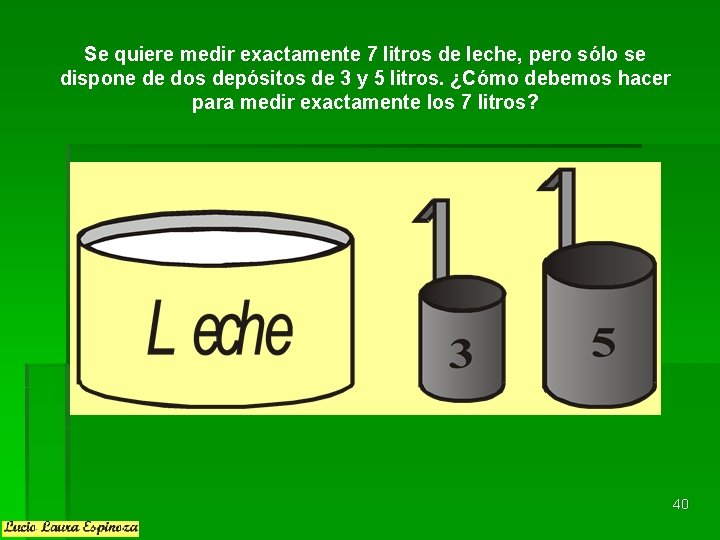
Se quiere medir exactamente 7 litros de leche, pero sólo se dispone de dos depósitos de 3 y 5 litros. ¿Cómo debemos hacer para medir exactamente los 7 litros? 40

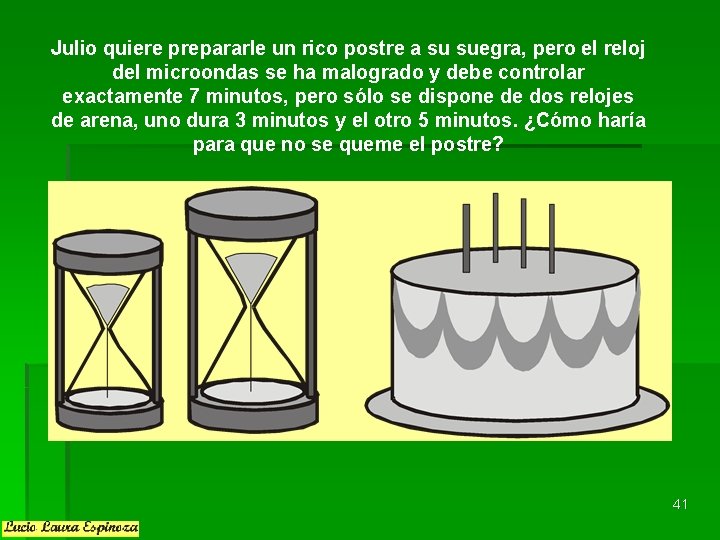
Julio quiere prepararle un rico postre a su suegra, pero el reloj del microondas se ha malogrado y debe controlar exactamente 7 minutos, pero sólo se dispone de dos relojes de arena, uno dura 3 minutos y el otro 5 minutos. ¿Cómo haría para que no se queme el postre? 41

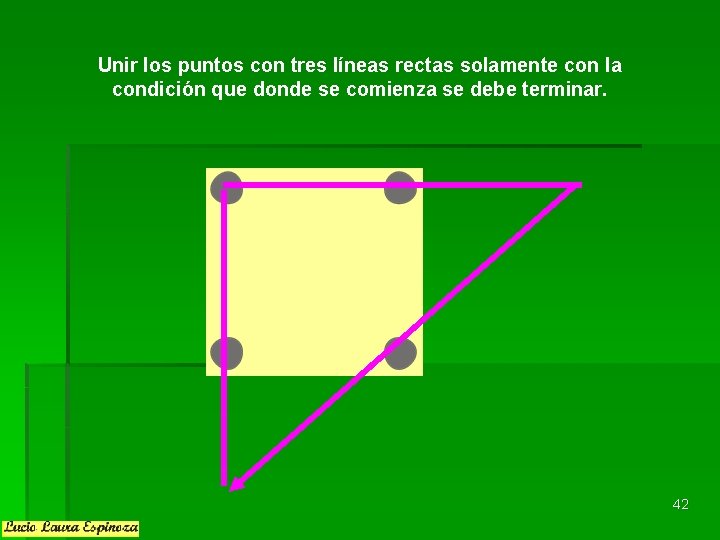
Unir los puntos con tres líneas rectas solamente con la condición que donde se comienza se debe terminar. 42

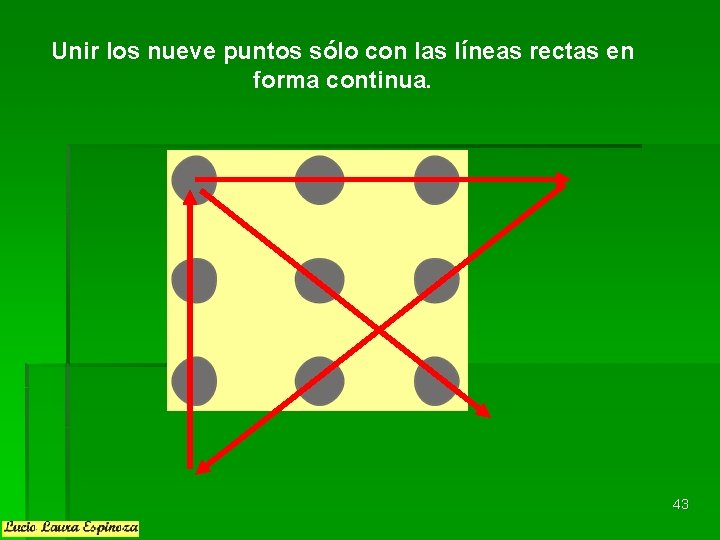
Unir los nueve puntos sólo con las líneas rectas en forma continua. 43

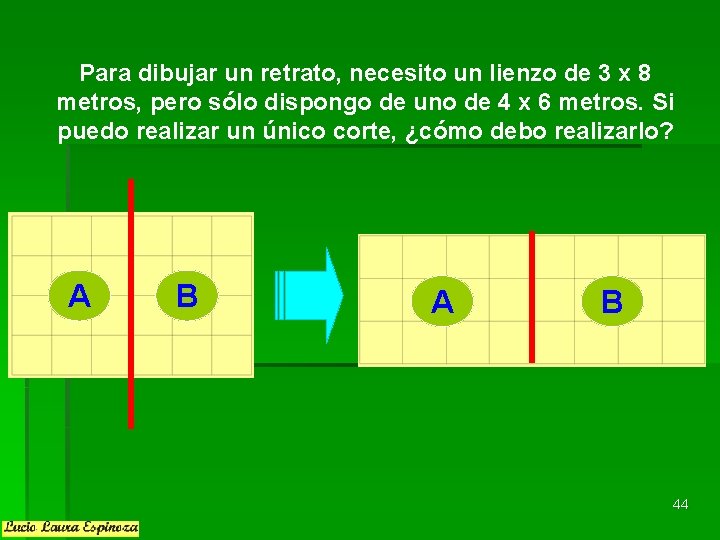
Para dibujar un retrato, necesito un lienzo de 3 x 8 metros, pero sólo dispongo de uno de 4 x 6 metros. Si puedo realizar un único corte, ¿cómo debo realizarlo? A B 44

El salto del caballo Colocando el número 1 en cualquier casillero, ir llenando los cuadrados con los siguientes números consecutivos hasta el 12, siguiendo el movimiento del caballo de ajedrez. 1 4 7 10 8 11 2 5 3 6 9 12 45

Colocar los números del 1 al 7, de tal manera que los números de arriba sean el resultado de la suma de los de abajo. 46

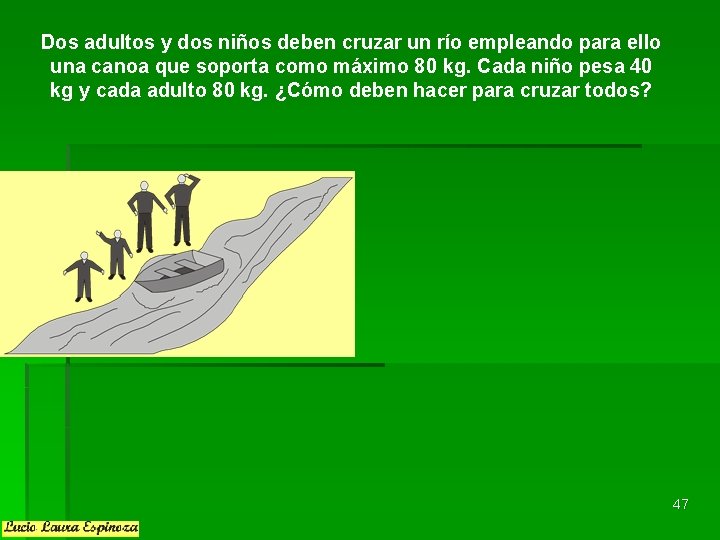
Dos adultos y dos niños deben cruzar un río empleando para ello una canoa que soporta como máximo 80 kg. Cada niño pesa 40 kg y cada adulto 80 kg. ¿Cómo deben hacer para cruzar todos? 47

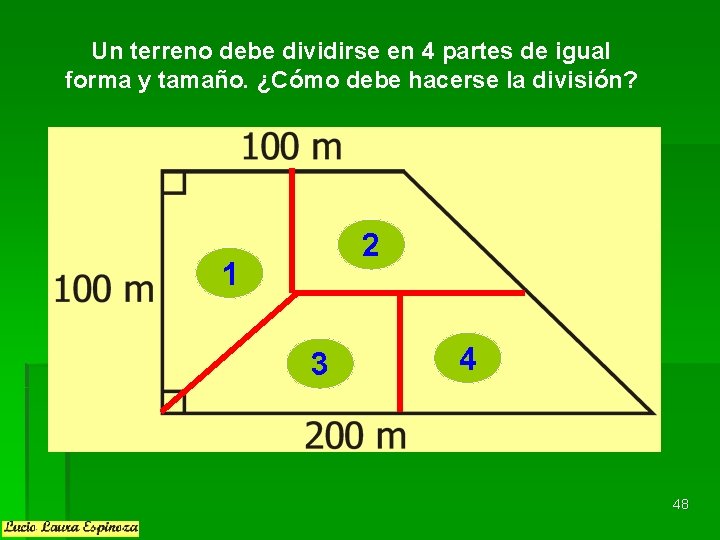
Un terreno debe dividirse en 4 partes de igual forma y tamaño. ¿Cómo debe hacerse la división? 2 1 3 4 48

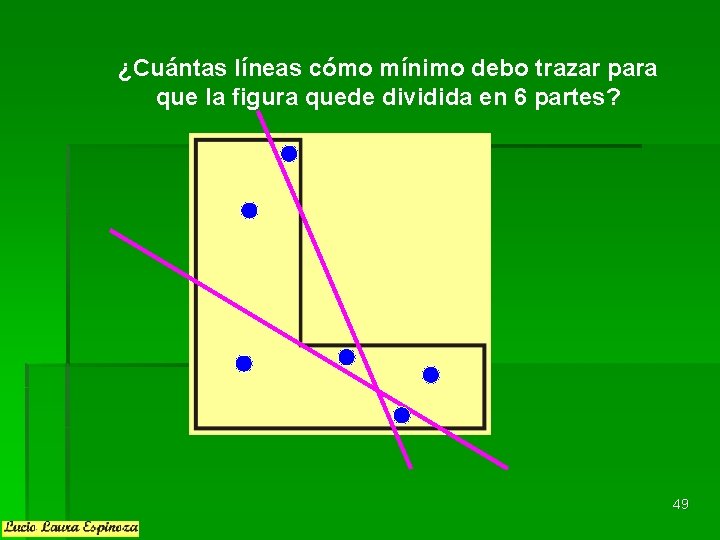
¿Cuántas líneas cómo mínimo debo trazar para que la figura quede dividida en 6 partes? 49

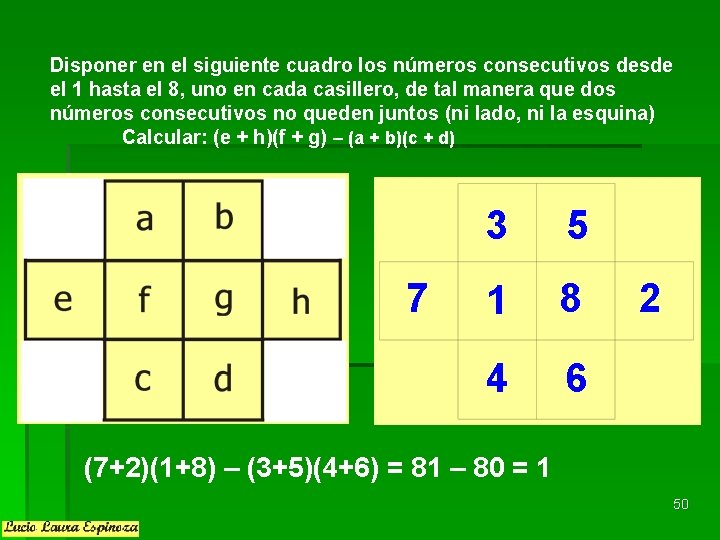
Disponer en el siguiente cuadro los números consecutivos desde el 1 hasta el 8, uno en cada casillero, de tal manera que dos números consecutivos no queden juntos (ni lado, ni la esquina) Calcular: (e + h)(f + g) – (a + b)(c + d) 7 3 5 1 8 4 6 2 (7+2)(1+8) – (3+5)(4+6) = 81 – 80 = 1 50

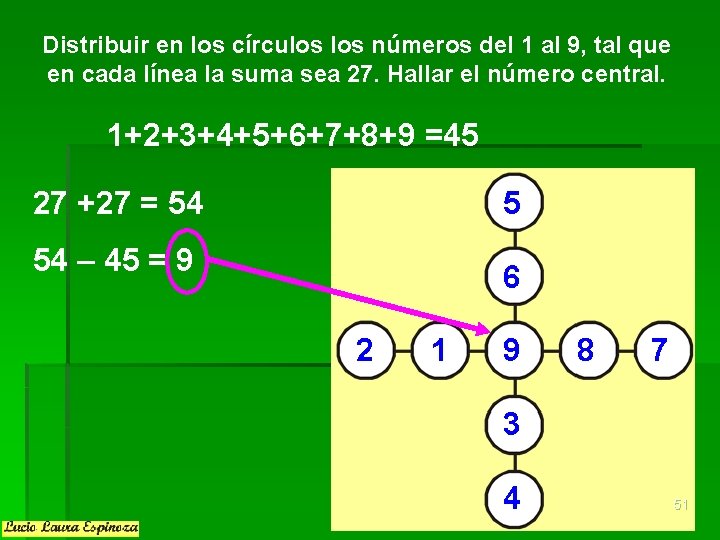
Distribuir en los círculos números del 1 al 9, tal que en cada línea la suma sea 27. Hallar el número central. 1+2+3+4+5+6+7+8+9 =45 27 +27 = 54 5 54 – 45 = 9 6 2 1 9 8 7 3 4 51

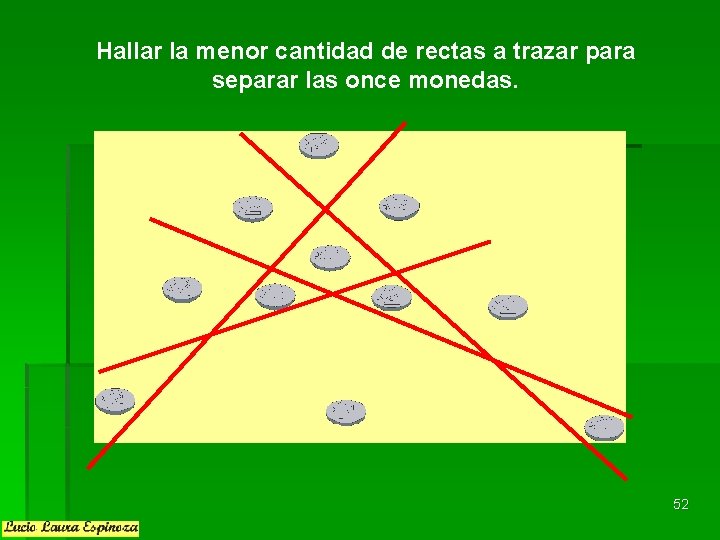
Hallar la menor cantidad de rectas a trazar para separar las once monedas. 52

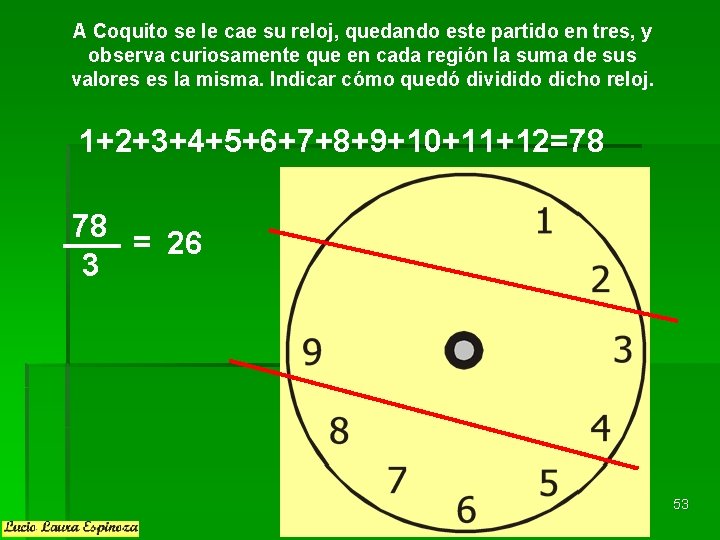
A Coquito se le cae su reloj, quedando este partido en tres, y observa curiosamente que en cada región la suma de sus valores es la misma. Indicar cómo quedó dividido dicho reloj. 1+2+3+4+5+6+7+8+9+10+11+12=78 78 = 26 3 53

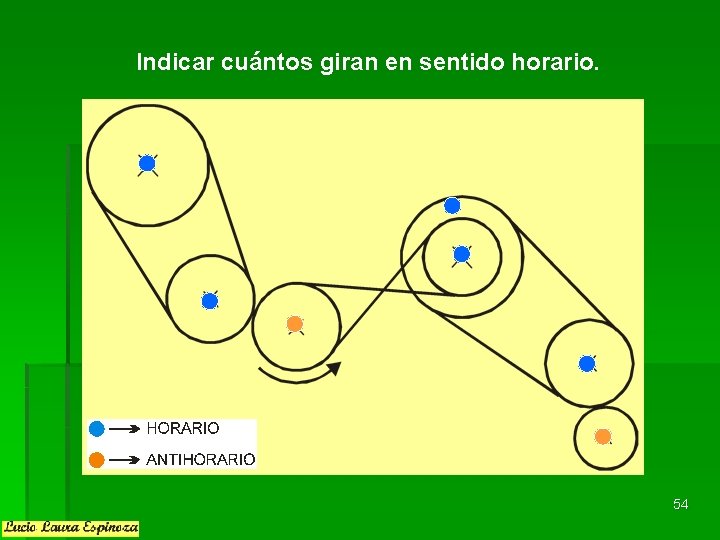
Indicar cuántos giran en sentido horario. 54

Colocar los números del 1 al 8, de tal forma que en cada ficha la suma sea la misma. Dar como respuesta la misma suma. 1+2+3+4+5+6+7+8=36 6 36 = 9 4 3 1 2 8 7 4 5 55

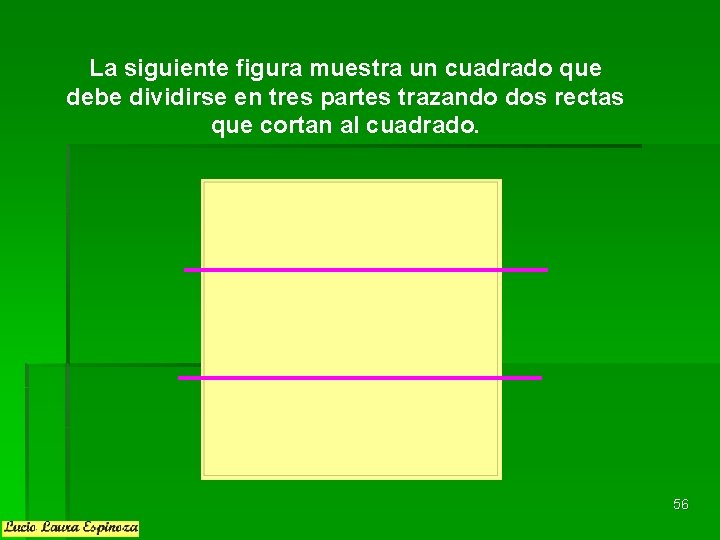
La siguiente figura muestra un cuadrado que debe dividirse en tres partes trazando dos rectas que cortan al cuadrado. 56

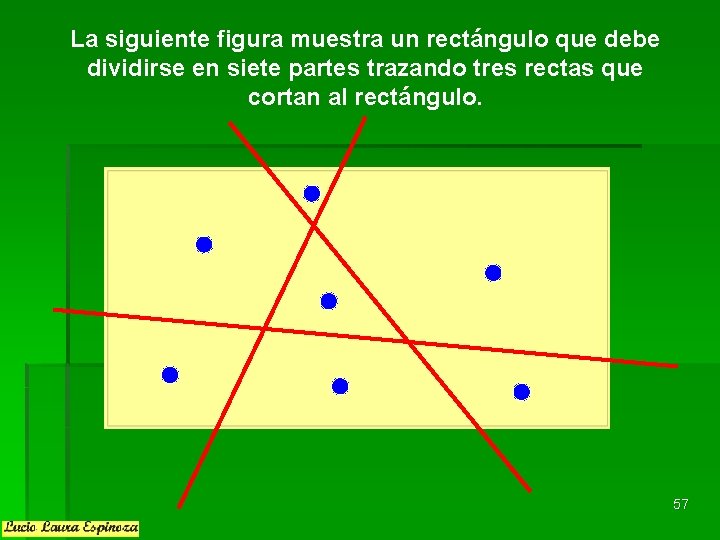
La siguiente figura muestra un rectángulo que debe dividirse en siete partes trazando tres rectas que cortan al rectángulo. 57

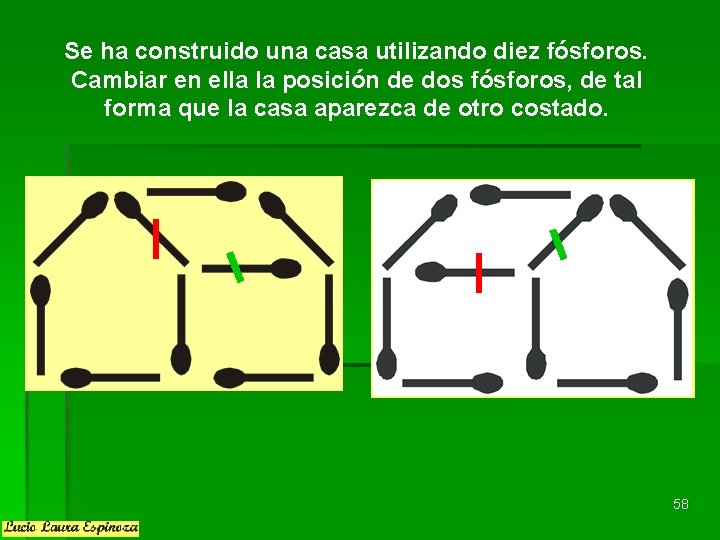
Se ha construido una casa utilizando diez fósforos. Cambiar en ella la posición de dos fósforos, de tal forma que la casa aparezca de otro costado. 58

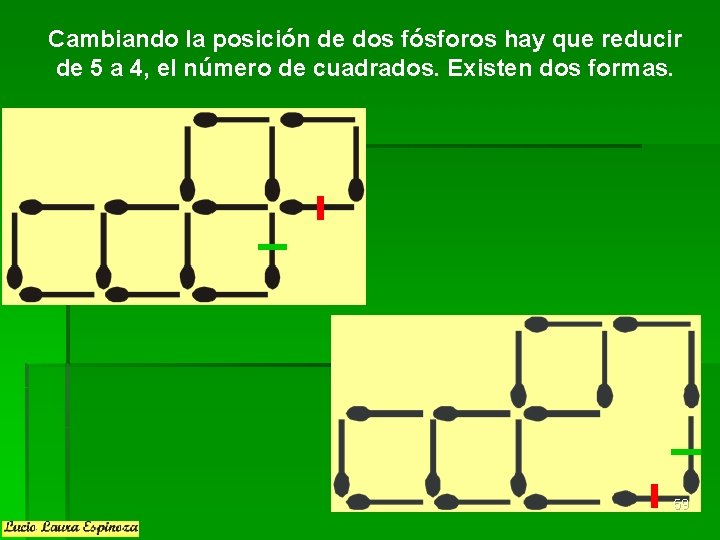
Cambiando la posición de dos fósforos hay que reducir de 5 a 4, el número de cuadrados. Existen dos formas. 59

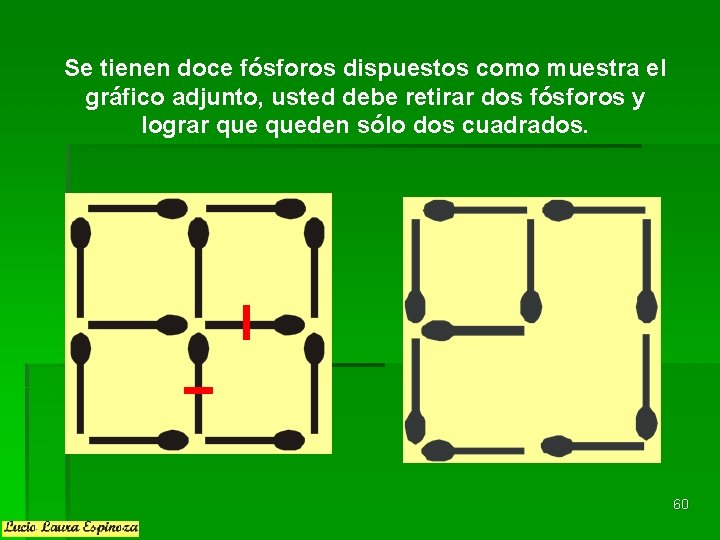
Se tienen doce fósforos dispuestos como muestra el gráfico adjunto, usted debe retirar dos fósforos y lograr queden sólo dos cuadrados. 60

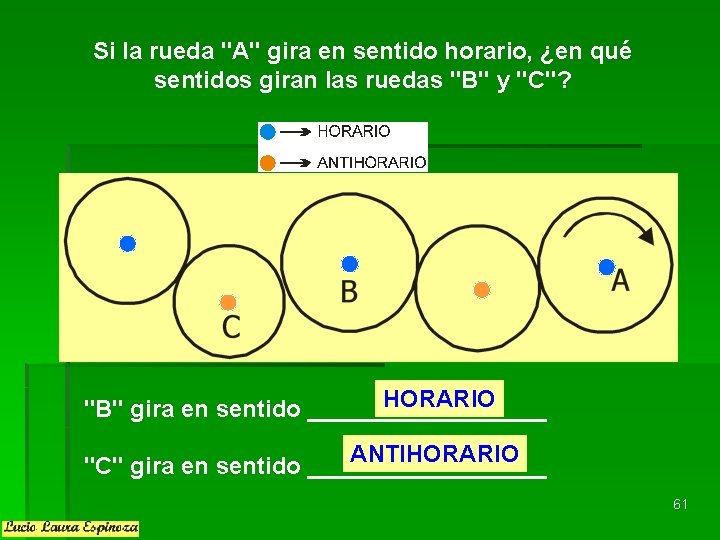
Si la rueda "A" gira en sentido horario, ¿en qué sentidos giran las ruedas "B" y "C"? HORARIO "B" gira en sentido _________ ANTIHORARIO "C" gira en sentido _________ 61

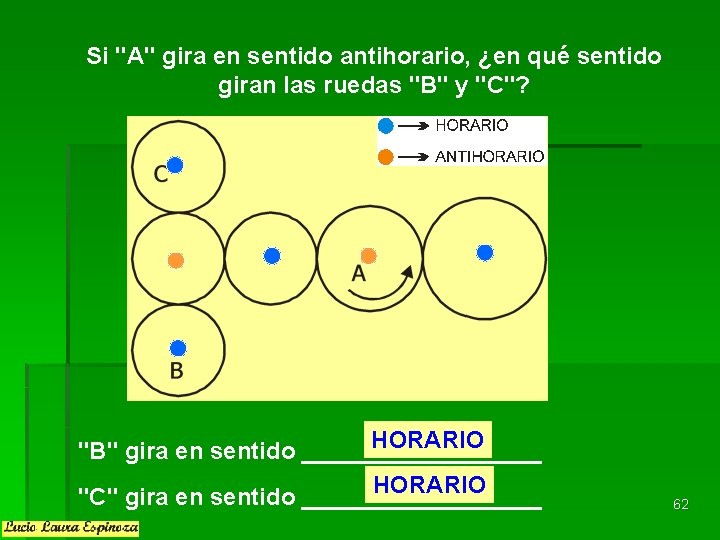
Si "A" gira en sentido antihorario, ¿en qué sentido giran las ruedas "B" y "C"? HORARIO "B" gira en sentido _________ HORARIO "C" gira en sentido _________ 62

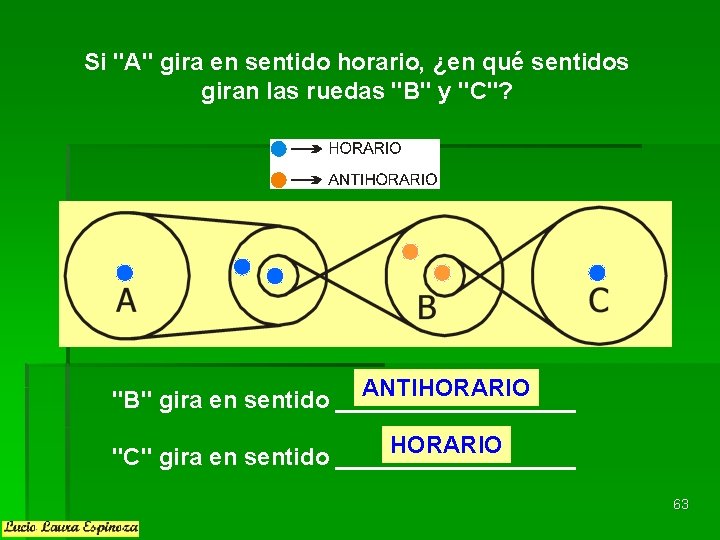
Si "A" gira en sentido horario, ¿en qué sentidos giran las ruedas "B" y "C"? ANTIHORARIO "B" gira en sentido _________ HORARIO "C" gira en sentido _________ 63

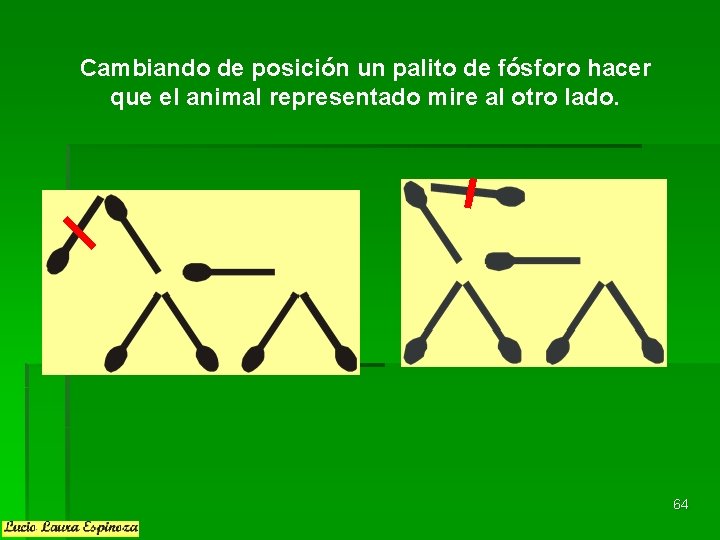
Cambiando de posición un palito de fósforo hacer que el animal representado mire al otro lado. 64

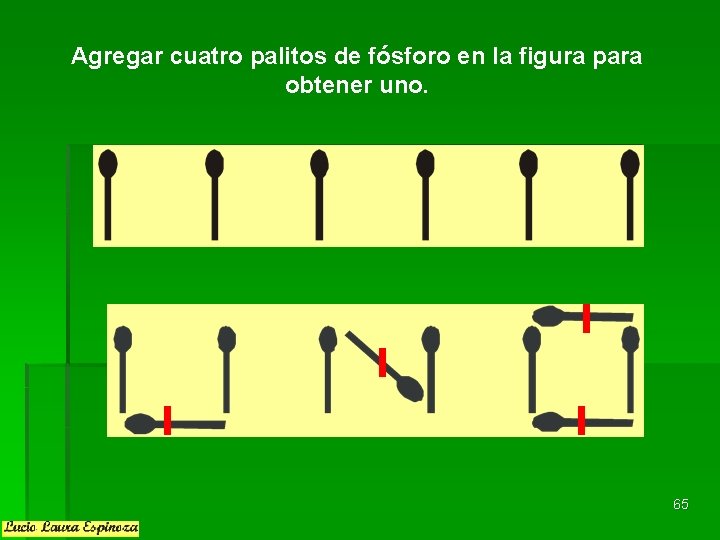
Agregar cuatro palitos de fósforo en la figura para obtener uno. 65

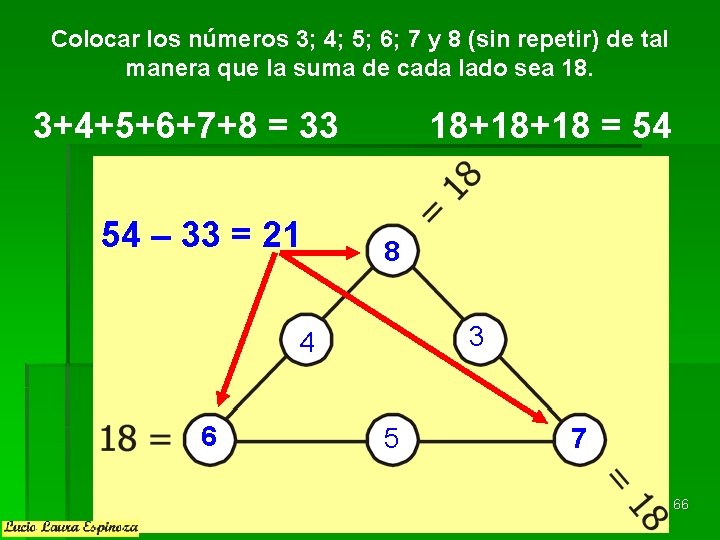
Colocar los números 3; 4; 5; 6; 7 y 8 (sin repetir) de tal manera que la suma de cada lado sea 18. 3+4+5+6+7+8 = 33 54 – 33 = 21 18+18+18 = 54 8 3 4 6 5 7 66

En las casillas de esta cuadrícula se han distribuido como puede verse 36 ceros. Hay que tachar doce ceros, pero de tal modo que después de esto, en cada fila y en cada columna quede el mismo número de ceros sin tachar. ¿Qué ceros hay que tachar? 67

Complete los números que faltan en los casilleros, teniendo en cuenta que la suma de dos números consecutivos de cualquier fila debe dar el número superior, sin repetirse. 4 2 1 68

Complete los números que faltan en los casilleros, teniendo en cuenta que la suma de dos números juntos de cualquier fila debe dar el número superior, sin repetirse. 8 5 1 18 6 69

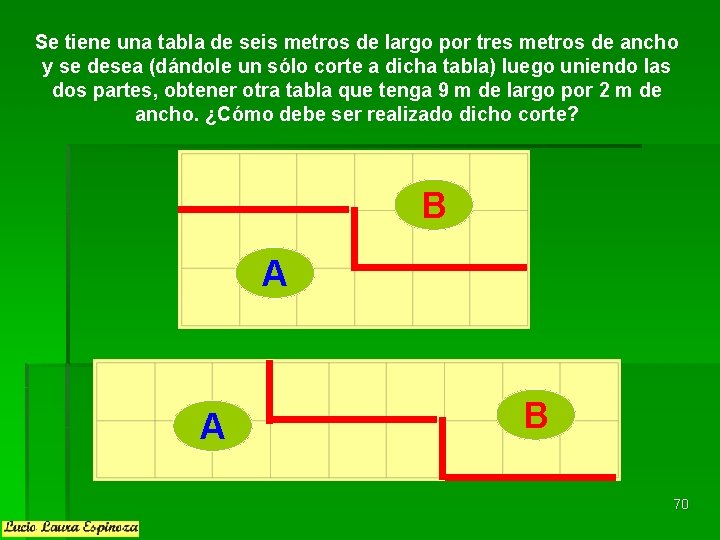
Se tiene una tabla de seis metros de largo por tres metros de ancho y se desea (dándole un sólo corte a dicha tabla) luego uniendo las dos partes, obtener otra tabla que tenga 9 m de largo por 2 m de ancho. ¿Cómo debe ser realizado dicho corte? B A A B 70

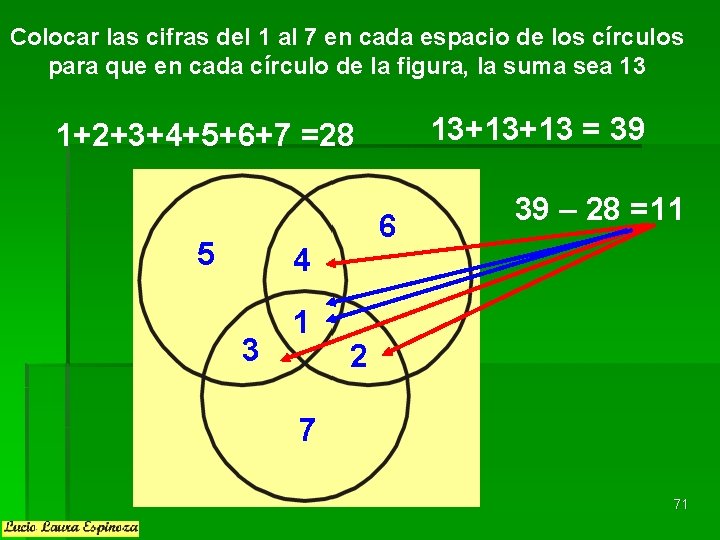
Colocar las cifras del 1 al 7 en cada espacio de los círculos para que en cada círculo de la figura, la suma sea 13 13+13+13 = 39 1+2+3+4+5+6+7 =28 5 6 4 3 1 39 – 28 =11 2 7 71

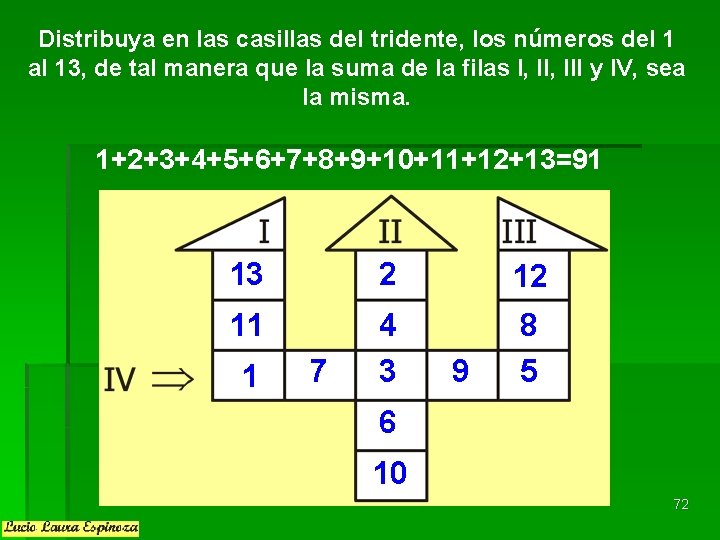
Distribuya en las casillas del tridente, los números del 1 al 13, de tal manera que la suma de la filas I, III y IV, sea la misma. 1+2+3+4+5+6+7+8+9+10+11+12+13=91 13 2 12 11 4 3 8 5 1 7 9 6 10 72

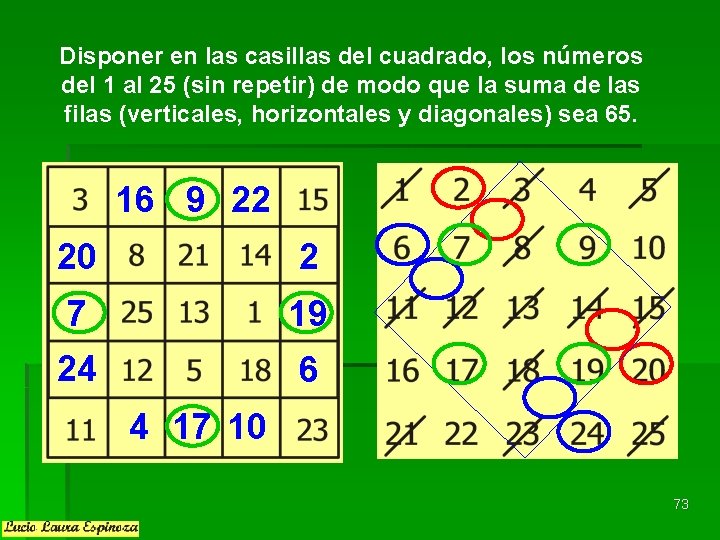
Disponer en las casillas del cuadrado, los números del 1 al 25 (sin repetir) de modo que la suma de las filas (verticales, horizontales y diagonales) sea 65. 16 9 22 20 2 7 19 24 6 4 17 10 73

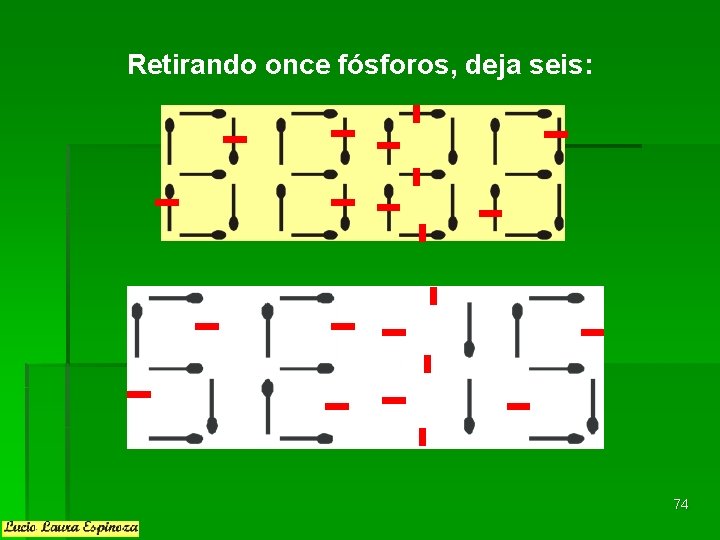
Retirando once fósforos, deja seis: 74

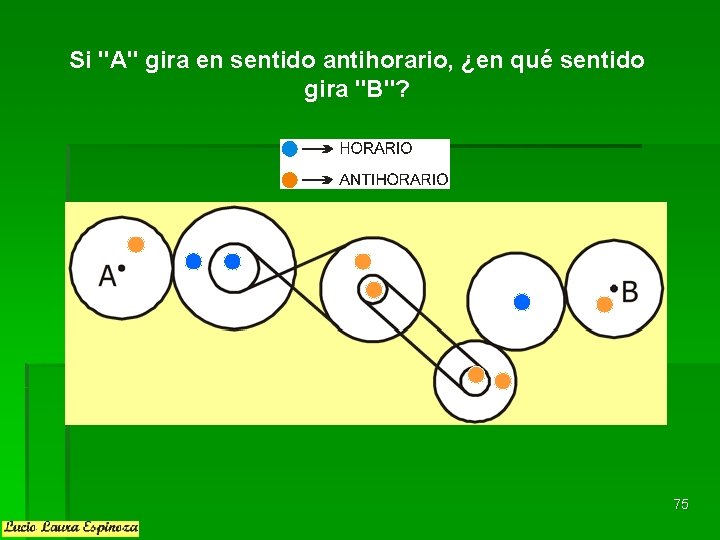
Si "A" gira en sentido antihorario, ¿en qué sentido gira "B"? 75

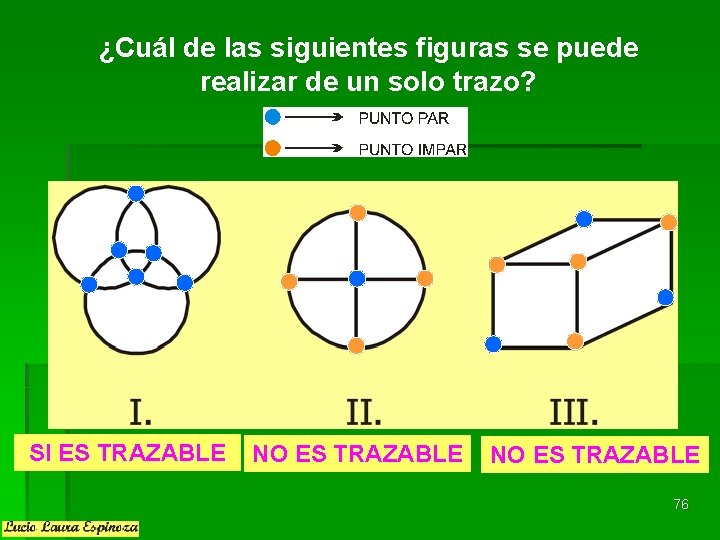
¿Cuál de las siguientes figuras se puede realizar de un solo trazo? SI ES TRAZABLE NO ES TRAZABLE 76

Complete los números que faltan en los casilleros, teniendo en cuenta que la suma de dos números juntos (consecutivos) de cualquier fila debe dar el número en el nivel inmediato superior, sin repetirse 31 12 19 11 1 5 77

Dividir la figura mostrada, en cuatro partes exactamente iguales en forma y tamaño. 78

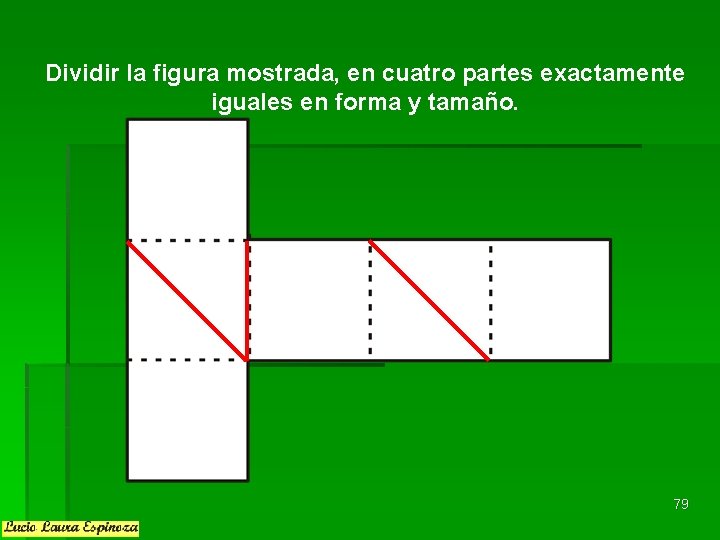
Dividir la figura mostrada, en cuatro partes exactamente iguales en forma y tamaño. 79

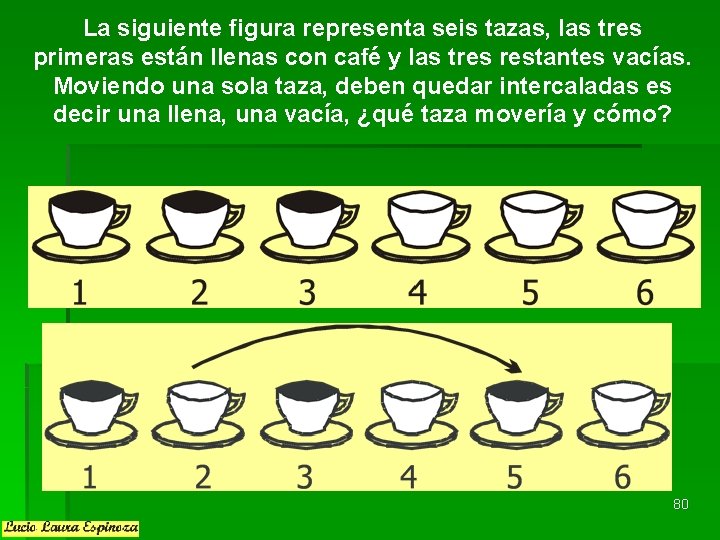
La siguiente figura representa seis tazas, las tres primeras están llenas con café y las tres restantes vacías. Moviendo una sola taza, deben quedar intercaladas es decir una llena, una vacía, ¿qué taza movería y cómo? 80

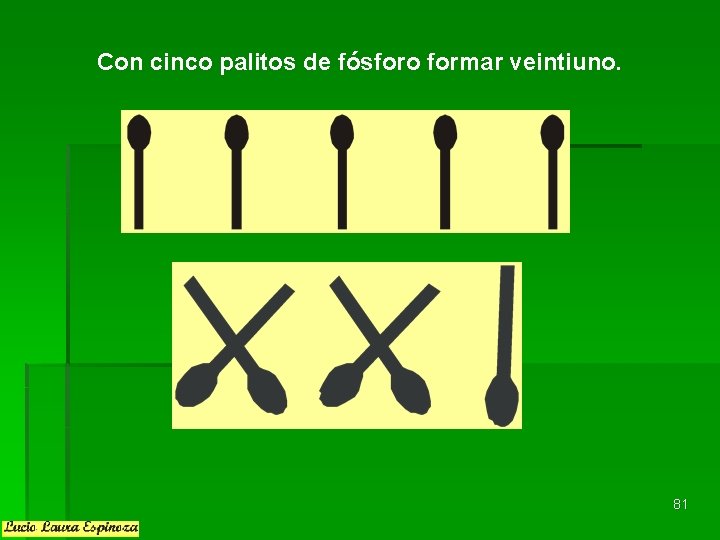
Con cinco palitos de fósforo formar veintiuno. 81

¿En qué condición se cumple que 11 + 3 = 2? 82

Escriba la palabra "DOSIS" en los tres casilleros mostrados (un carácter por casilla). 2 I I 83

¿Qué contiene la caja mostrada? 84

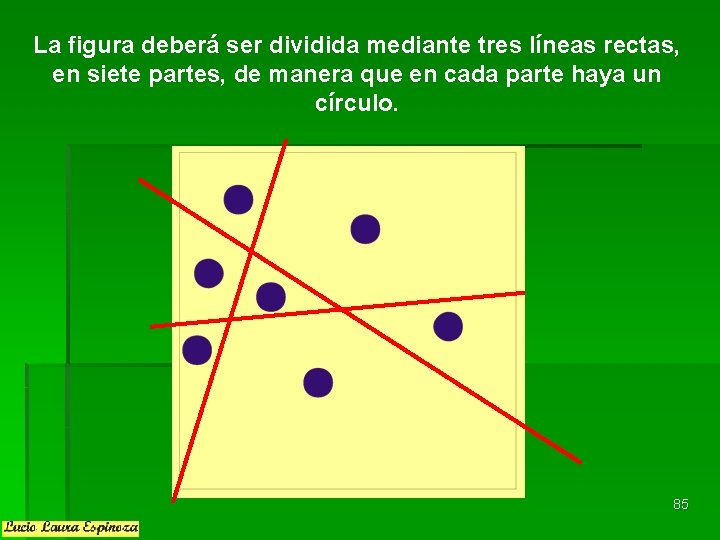
La figura deberá ser dividida mediante tres líneas rectas, en siete partes, de manera que en cada parte haya un círculo. 85

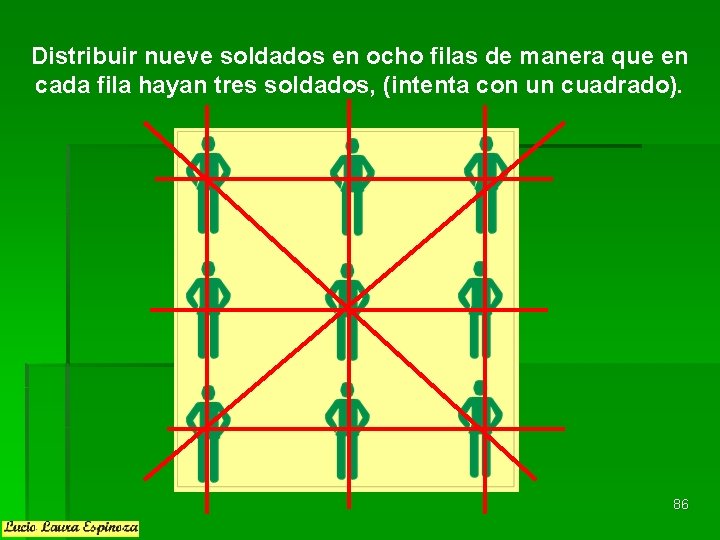
Distribuir nueve soldados en ocho filas de manera que en cada fila hayan tres soldados, (intenta con un cuadrado). 86

La siguiente columna de cinco filas contiene 15 cifras impares. El problema consiste en tachar nueve cifras, eligiéndolas de manera que al sumar las columnas de las seis restantes se obtenga el número 1111. 87

Utilizando seis cifras "1" y la operación suma, obtener el número 24. 11+11+1+1 = 24 88

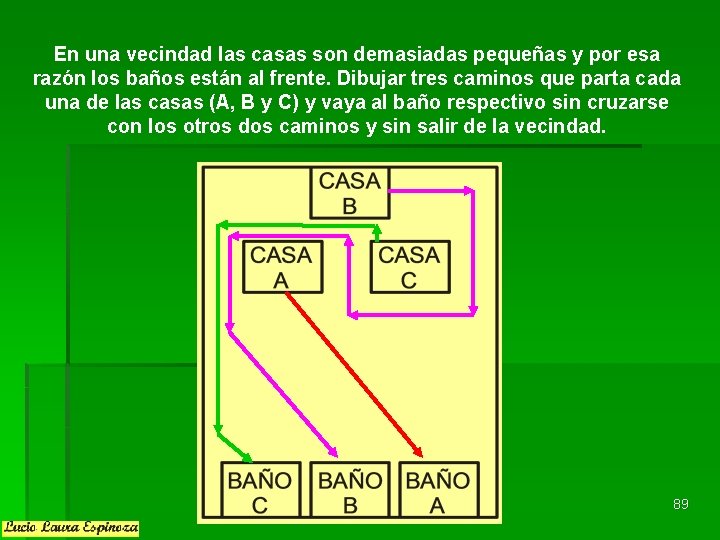
En una vecindad las casas son demasiadas pequeñas y por esa razón los baños están al frente. Dibujar tres caminos que parta cada una de las casas (A, B y C) y vaya al baño respectivo sin cruzarse con los otros dos caminos y sin salir de la vecindad. 89

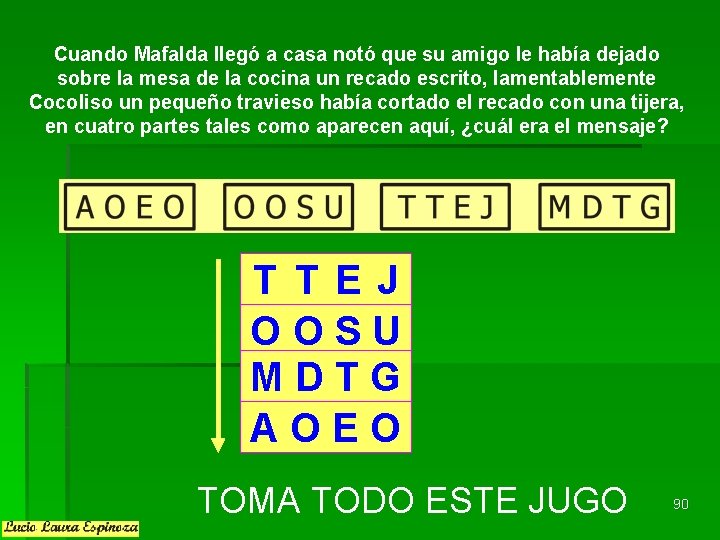
Cuando Mafalda llegó a casa notó que su amigo le había dejado sobre la mesa de la cocina un recado escrito, lamentablemente Cocoliso un pequeño travieso había cortado el recado con una tijera, en cuatro partes tales como aparecen aquí, ¿cuál era el mensaje? T TEJ OOSU MDTG AOEO TOMA TODO ESTE JUGO 90

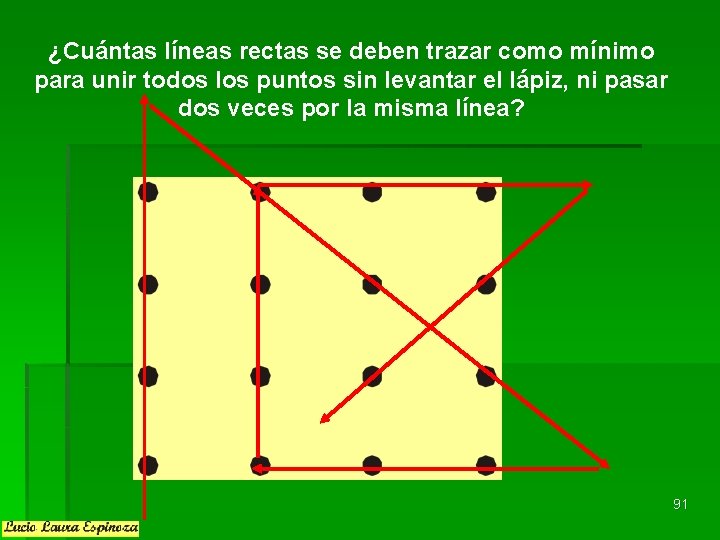
¿Cuántas líneas rectas se deben trazar como mínimo para unir todos los puntos sin levantar el lápiz, ni pasar dos veces por la misma línea? 91

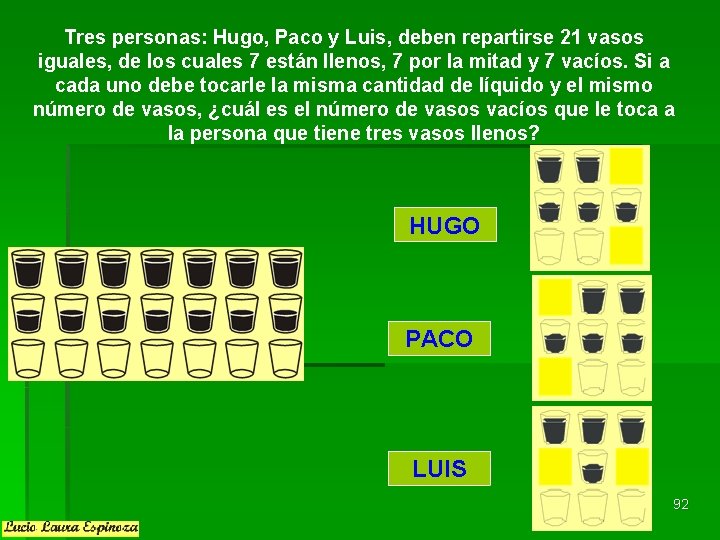
Tres personas: Hugo, Paco y Luis, deben repartirse 21 vasos iguales, de los cuales 7 están llenos, 7 por la mitad y 7 vacíos. Si a cada uno debe tocarle la misma cantidad de líquido y el mismo número de vasos, ¿cuál es el número de vasos vacíos que le toca a la persona que tiene tres vasos llenos? HUGO PACO LUIS 92

Dos amigos se detienen a servirse panes, uno llevó 5 panes y el otro 3. En ese momento se presenta otra persona a quien le invitan, los tres se reparten los panes en porciones iguales; al despedirse el invitado les obsequió S/. 8 para que se repartan. ¿Cuánto le correspondió a cada uno? 93

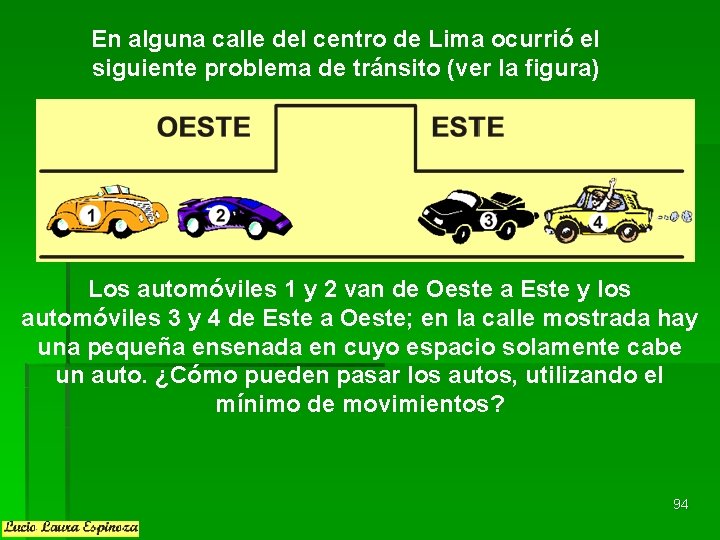
En alguna calle del centro de Lima ocurrió el siguiente problema de tránsito (ver la figura) Los automóviles 1 y 2 van de Oeste a Este y los automóviles 3 y 4 de Este a Oeste; en la calle mostrada hay una pequeña ensenada en cuyo espacio solamente cabe un auto. ¿Cómo pueden pasar los autos, utilizando el mínimo de movimientos? 94

Un bodeguero recibe tres paquetes con veinte caramelos cada uno. Los paquetes contienen respectivamente caramelos de naranja, limón y chicha morada. Además recibe con los paquetes una nota, indicando que hay un error en cuanto a las etiquetas; y que todas están equivocadas, ¿cuántos caramelos como mínimo tendrá que sacar el bodeguero para comprobar el contenido de los paquetes? 95

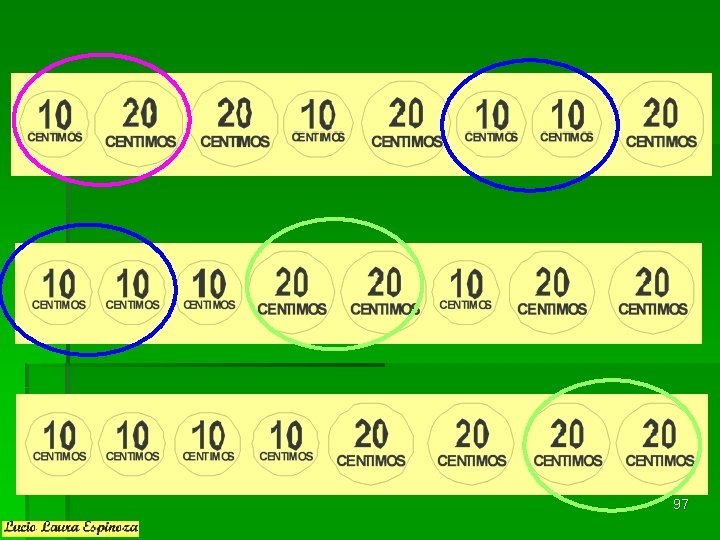
Ocho monedas, cuatro de 20 céntimos y cuatro de 10 céntimos van colocadas en fila y en forma alternada tal como lo muestra la figura. El juego consiste en mover dos monedas que se encuentran una al lado de la otra en forma conjunta, sin intercambiarlas de un lado a otro. Esto deberá repetirse hasta obtener, con sólo cuatro movimientos de este tipo, una fila donde estén las cuatro grandes y las cuatro pequeñas juntas, todas con la misma distancia entre sí como al principio. ¿Cómo lo harías? 96

97

En la siguiente expresión, mover una cifra para que se verifique la igualdad: 23 + 2 = 10 3 2 + 2 = 10 98