Anyon and Topological Quantum Computation SuPeng Kou Beijing

Anyon and Topological Quantum Computation Su-Peng Kou Beijing Normal university

Outline 1. Part I: Anyons and braiding group 2. Part II: Quantum computation of topological qubits in Z 2 topological orders 3. Part III : Topological quantum computation by Ising anyons 4. IV: Topological quantum computation by Fibonacci anyons Key words: topological string operator, non. Abelian anyon

Milestone for topological quantum computation § 1997, Kitaev proposed the idea of topological quantum bit and fault torrent quantum computation in an Abelian state. § 2001, Kitaev proposed the topological quantum compuation by braiding non. Abelian anyons. § 2001, Preskill, Freedman and others proposed a universal topological quantum computation.
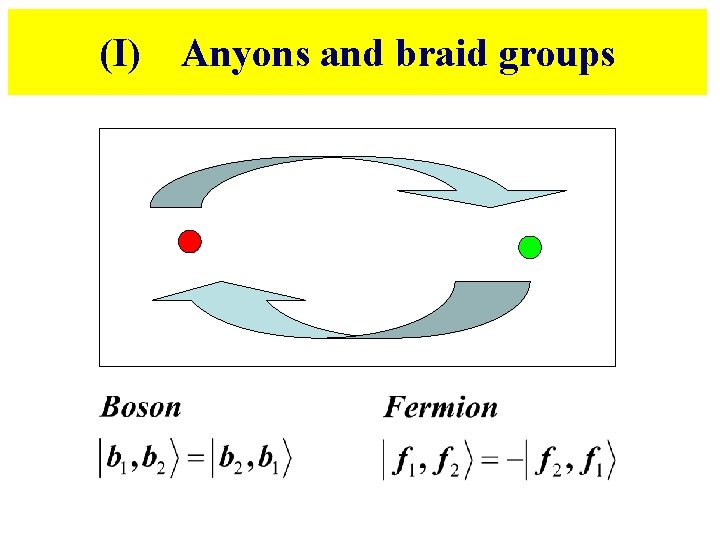
(I) Anyons and braid groups

Abelian statistics via non-Abelian statistics
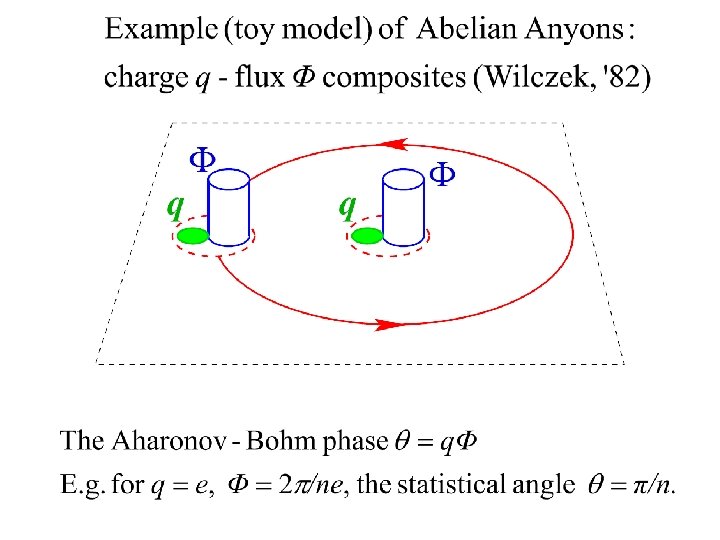
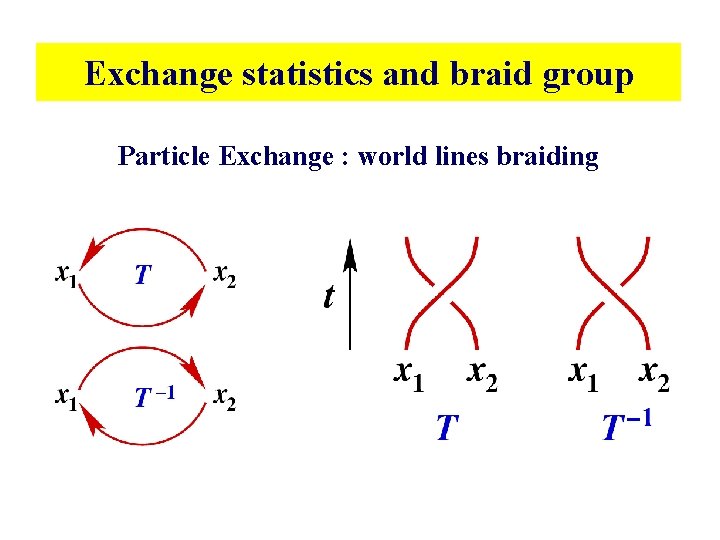
Exchange statistics and braid group Particle Exchange : world lines braiding
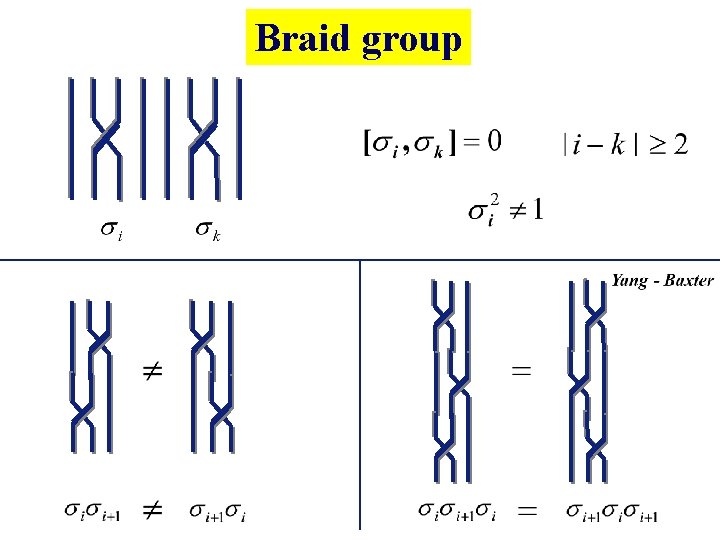
Braid group

General anyon theory 1. A finite set of quasi-particles or anyonic “charges. ” 2. Fusion rules (specifying how charges Fusion rules can combine or split). 3. Braiding rules (specifying behavior under Braiding rules particle exchange).
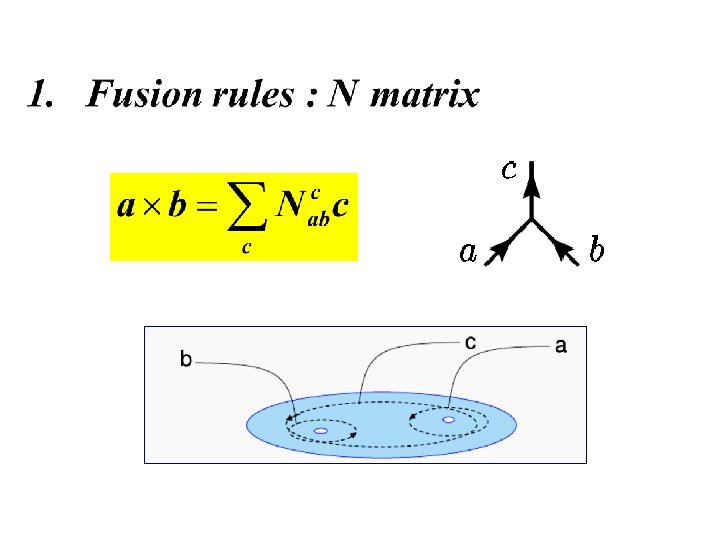
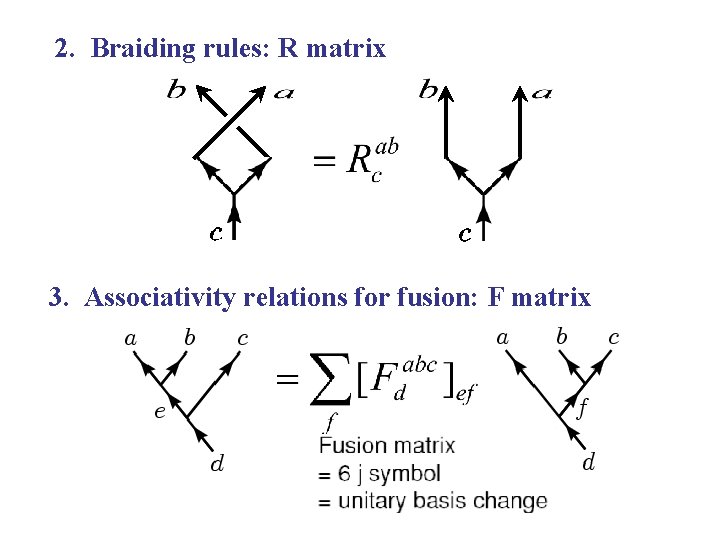
2. Braiding rules: R matrix 3. Associativity relations for fusion: F matrix
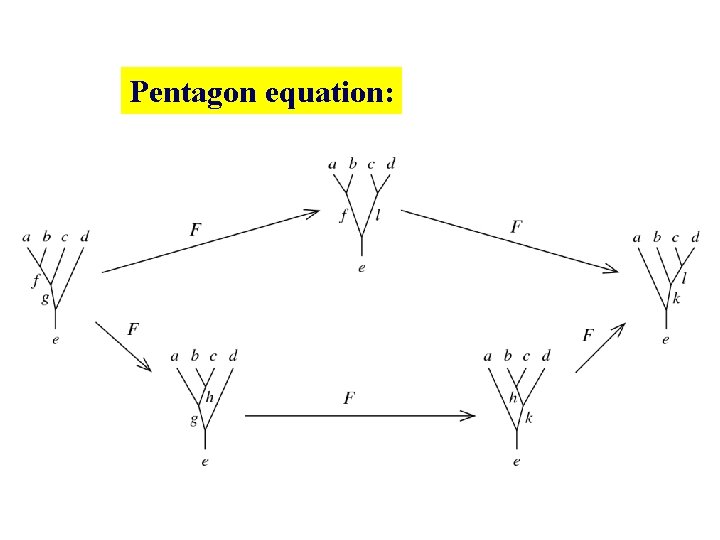
Pentagon equation:
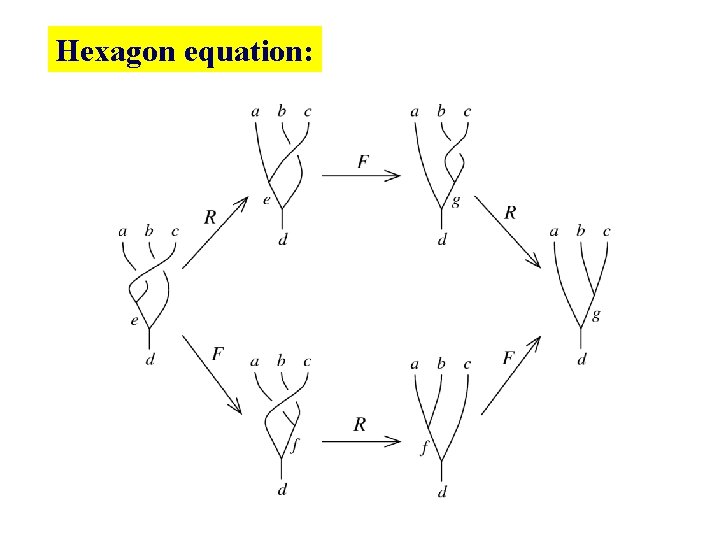
Hexagon equation:

Non-Abelian statistics Exchanging particles 1 and 2: Exchanging particles 2 and 3: • Matrices M 12 and M 23 don’t commute; • Matrices M form a higher-dimensional representation of the braid-group.

(II) Quantum computation of topological qubits in Z 2 topological orders

1. Z 2 topological order 1. There are four sectors : I (vacuum), ε(fermion), e (Z 2 charge), m (Z 2 vortex) ; 2. Z 2 gauge theory 3. U(1)×U(1) mutual Chern-Simons theory 4. Topological degeneracy : 4 on torus SP Kou, M Levin, and XG Wen, PRB 78, 155134 (2008).
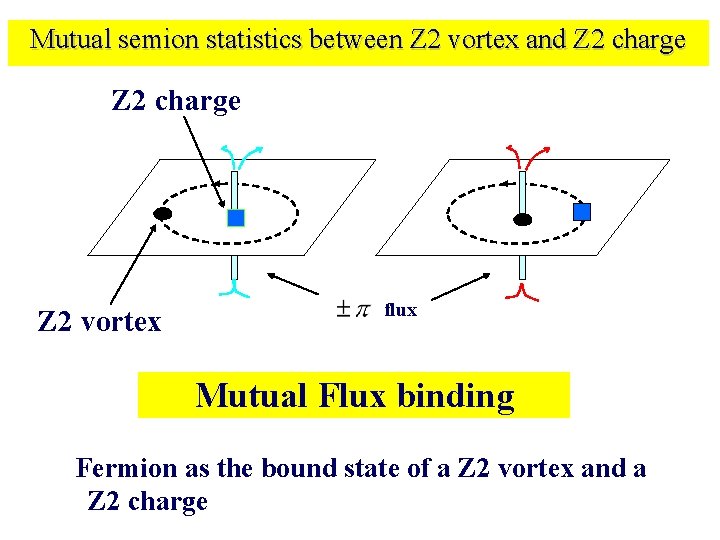
Mutual semion statistics between Z 2 vortex and Z 2 charge Z 2 vortex flux Mutual Flux binding Fermion as the bound state of a Z 2 vortex and a Z 2 charge
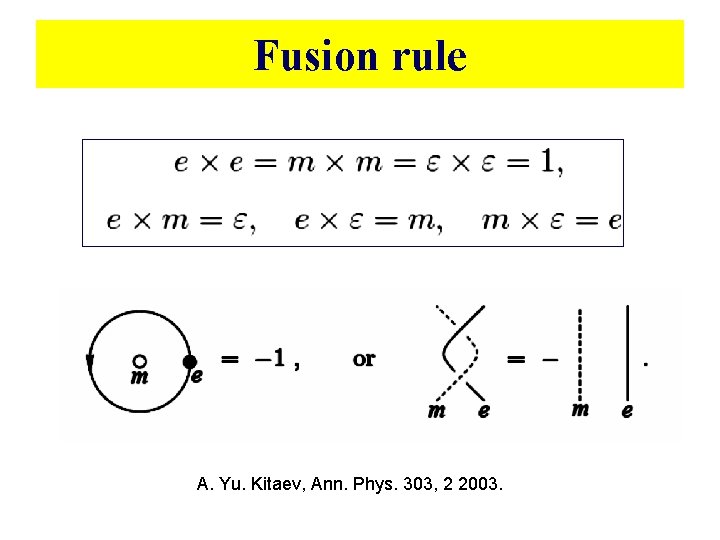
Fusion rule A. Yu. Kitaev, Ann. Phys. 303, 2 2003.
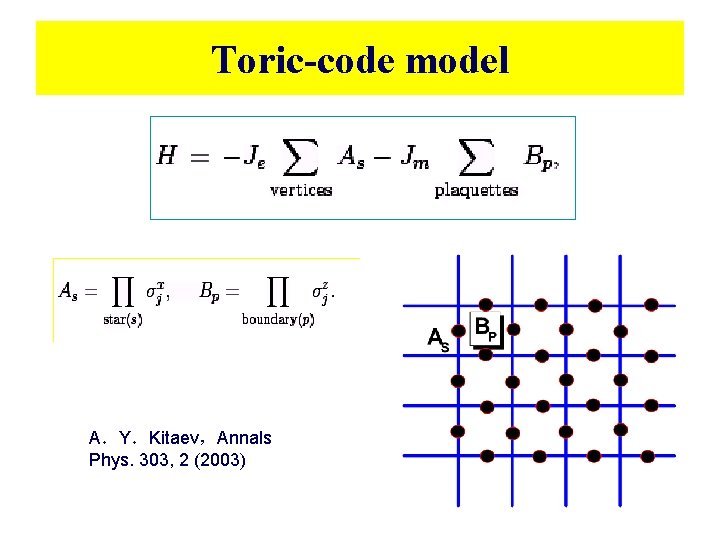
Toric-code model A.Y.Kitaev,Annals Phys. 303, 2 (2003)
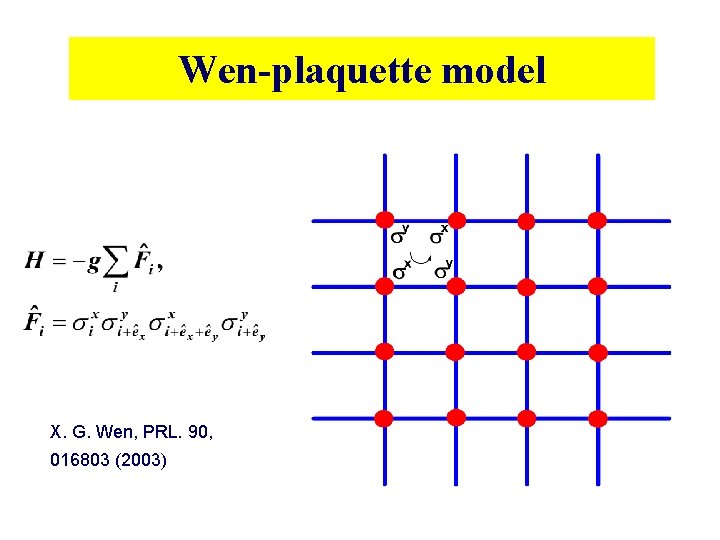
Wen-plaquette model X. G. Wen, PRL. 90, 016803 (2003)

Solving the Wen-plaquette model • The energy eigenstates are labeled by the eigenstates of • Because of , the eigenvalues are
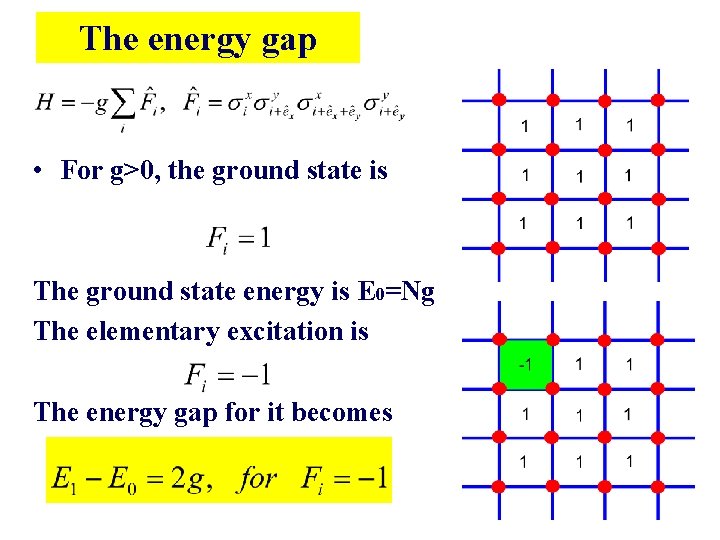
The energy gap • For g>0, the ground state is The ground state energy is E 0=Ng The elementary excitation is The energy gap for it becomes

The statistics for the elementary excitations • There are two kinds of Bosonic excitations: • Z 2 vortex • Z 2 charge • Each kind of excitations moves on each subplaquette: • Why?

• There are two constraints (the even-by-even lattice): One for the even plaquettes, the other for the odd plaquettes • The hopping from even plaquette to odd violates the constraints : You cannot change a Z 2 vortex into a Z 2 charge

Topological degeneracy on a torus (even-by-even lattice) : • On an even-by-even lattice, there are totally states • Under the constaints, the number of states are only • For the ground state , it must be four-fold degeneracy.
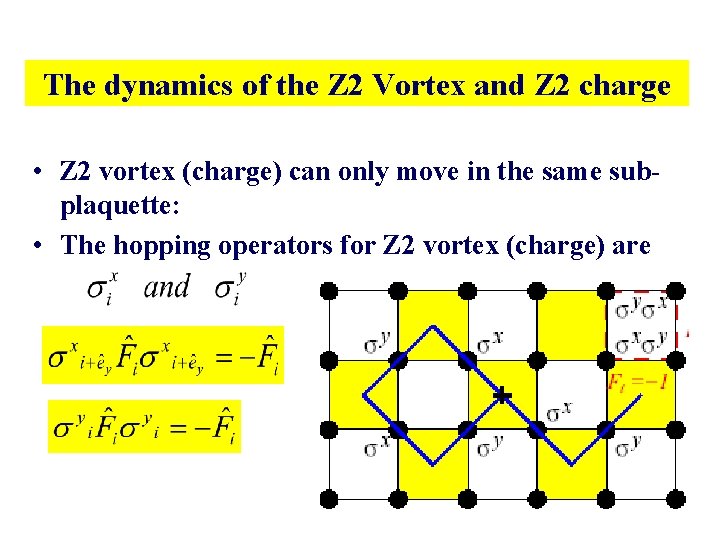
The dynamics of the Z 2 Vortex and Z 2 charge • Z 2 vortex (charge) can only move in the same subplaquette: • The hopping operators for Z 2 vortex (charge) are

The mutual semion statistics between the Z 2 Vortex and Z 2 charge • When an excitation (Z 2 vortex) in even-plaquette move around an excitation (Z 2 charge) in oddplaquette, the operator is • it is -1 with an excitation on it • This is the character for mutual semion statistics Fermion as the bound state of a Z 2 vortex and a Z 2 charge. X. G. Wen, PRD 68, 024501 (2003).
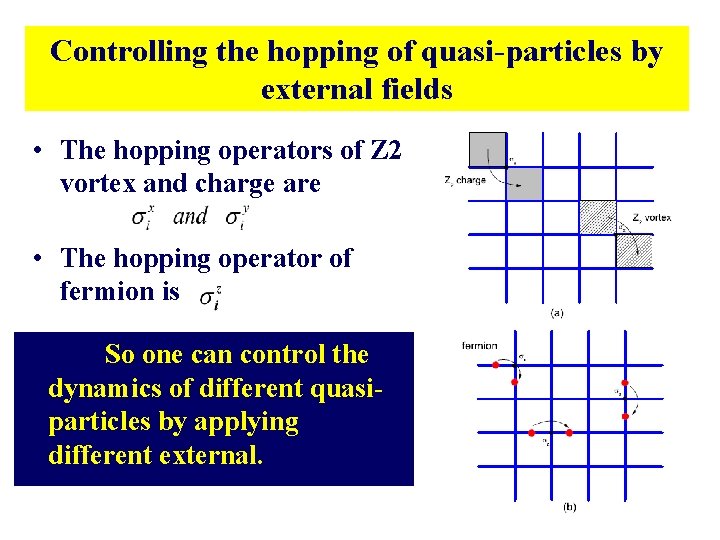
Controlling the hopping of quasi-particles by external fields • The hopping operators of Z 2 vortex and charge are • The hopping operator of fermion is So one can control the dynamics of different quasiparticles by applying different external.
• Closed strings • Open strings
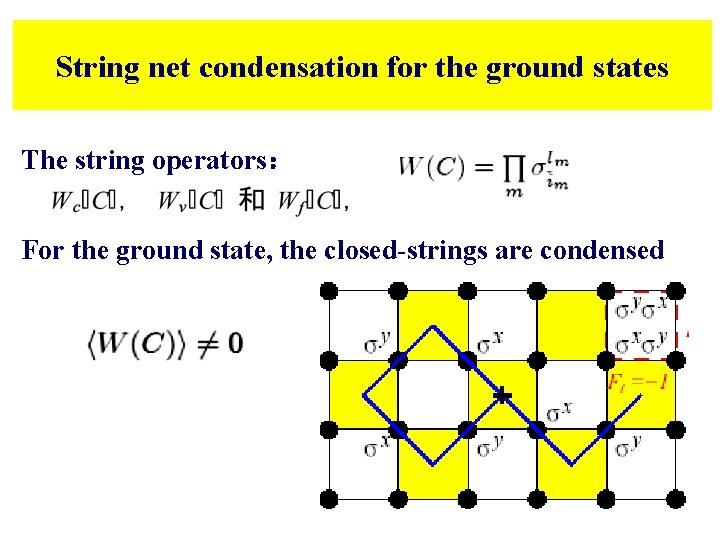
String net condensation for the ground states The string operators: For the ground state, the closed-strings are condensed

The toric-code model • There are two kinds of Bosonic excitations: • Z 2 vortex • Z 2 charge Fermion as the bound state of a Z 2 vortex and a Z 2 charge.

Controlling the hopping of quasi-particles by external fields • The hopping operator of Z 2 vortex is • The hopping operator of Z 2 charge is • The hopping operator of fermion is So one can control the dynamics of different quasi-particles by applying different external fields.

2. Topological qubit A. Yu. Kitaev, Annals Phys. 303, 2 (2003) |0> and |1> are the degenerate ground-states of a (Z 2) topological order due to the (non-trivial) topology. Advantage No local perturbation can introduce decoherence. Ioffe, &, Nature 415, 503 (2002)
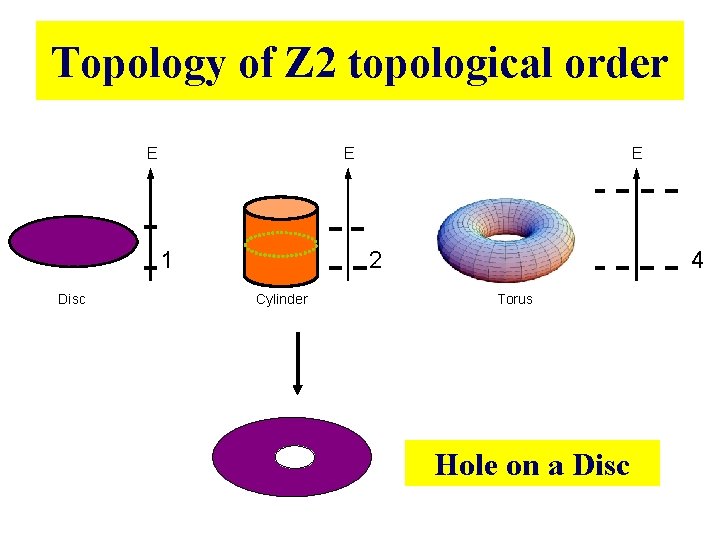
Topology of Z 2 topological order E E 1 Disc E 2 Cylinder 4 Torus Hole on a Disc

Topological closed string operators on torus – topological qubits

Degenerate ground states as eigenstates of topological closed operators • Algebra relationship: • Define pseudo-spin operators:

Topological closed string operators • On torus,pseudo-spin representation of topological closed string operators: S. P. Kou, PHYS. REV. LETT. 102, 120402 (2009). J. Yu and S. P. Kou, PHYS. REV. B 80, 075107 (2009). S. P. Kou, PHYS. REV. A 80, 052317 (2009).

Degenerate ground states as eigenstates of topological closed operators
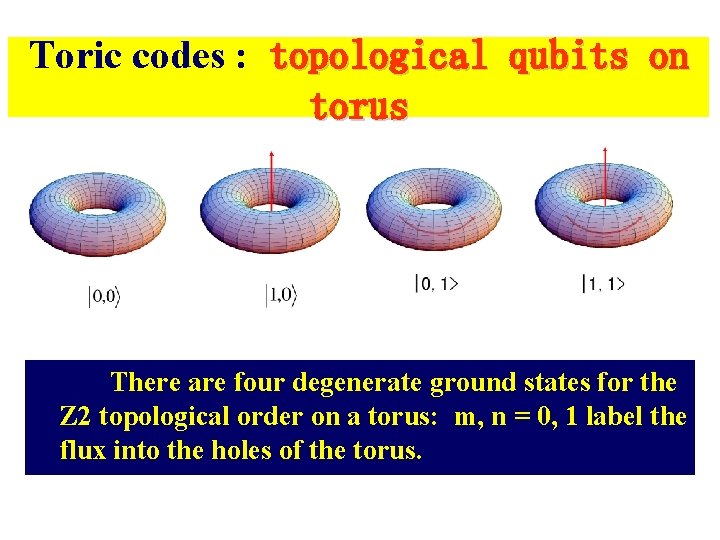
Toric codes : topological qubits on torus There are four degenerate ground states for the Z 2 topological order on a torus: m, n = 0, 1 label the flux into the holes of the torus.

How to control the topological qubits? A. Y. Kitaev : “Unfortunately, I do not know any way this quantum information can get in or out. Too few things can be done by moving abelian anyons. All other imaginable ways of accessing the ground state are uncontrollable. ” uncontrollable A.Y.Kitaev,Annals Phys. 303, 2 (2003)
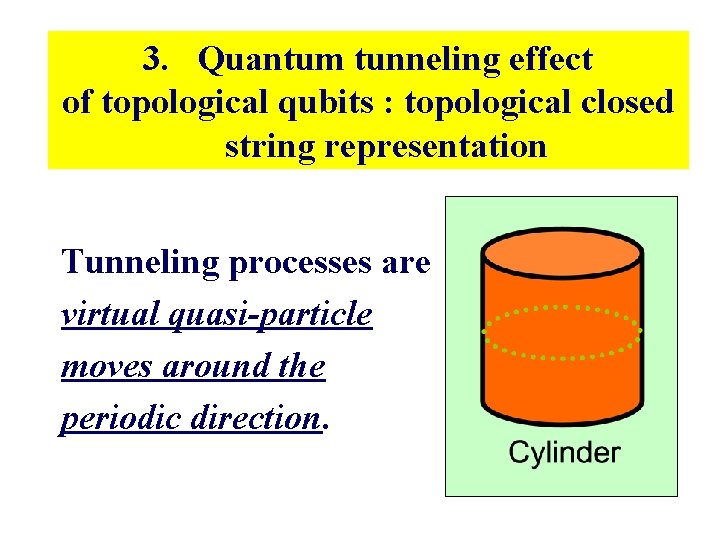
3. Quantum tunneling effect of topological qubits : topological closed string representation Tunneling processes are virtual quasi-particle moves around the periodic direction.
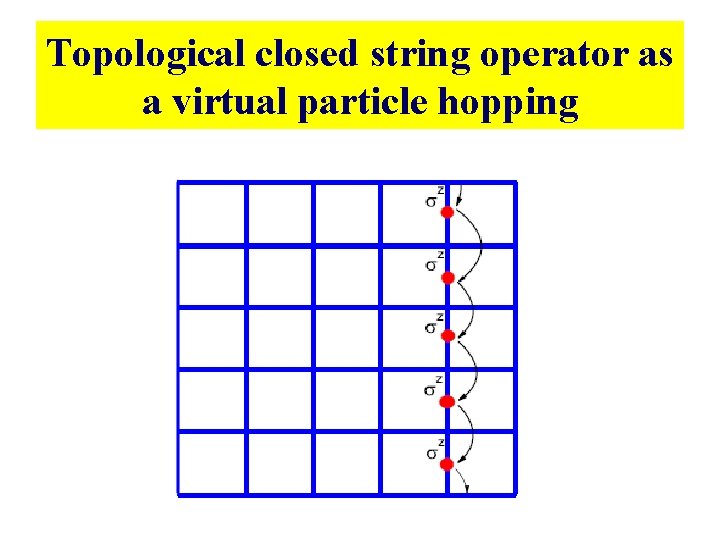
Topological closed string operator as a virtual particle hopping
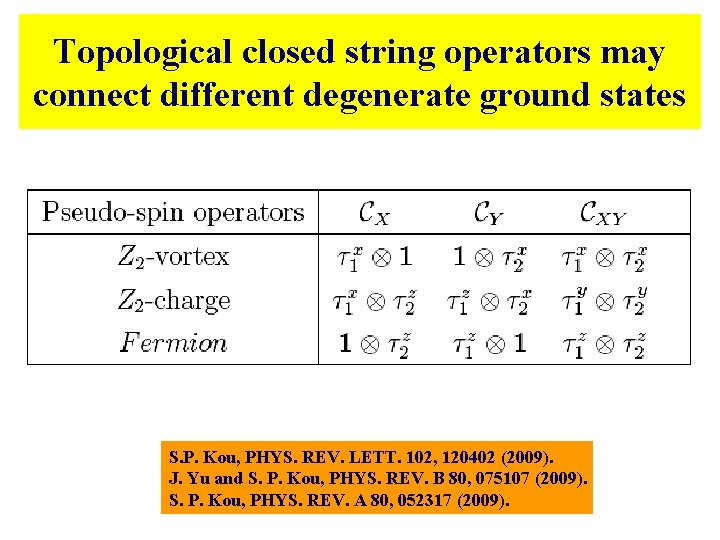
Topological closed string operators may connect different degenerate ground states S. P. Kou, PHYS. REV. LETT. 102, 120402 (2009). J. Yu and S. P. Kou, PHYS. REV. B 80, 075107 (2009). S. P. Kou, PHYS. REV. A 80, 052317 (2009).

Higher order perturbation approach • Energy splitting : lowest order contribution of topological closed string operators L 0 is the length of topological closed string operator
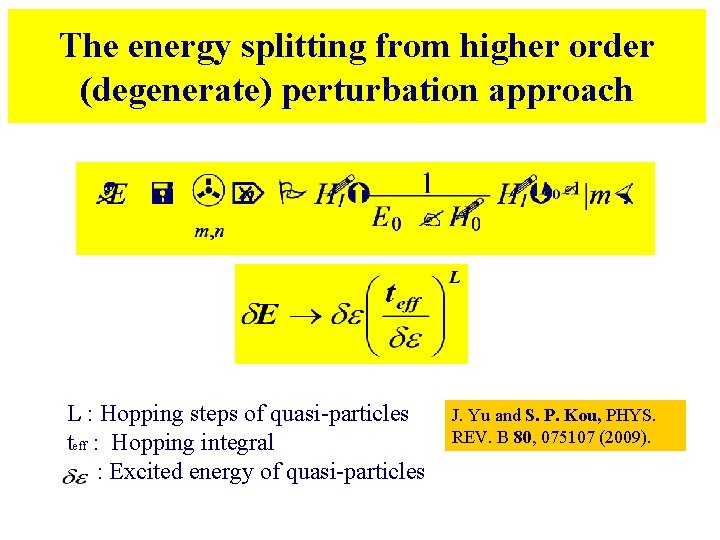
The energy splitting from higher order (degenerate) perturbation approach L : Hopping steps of quasi-particles teff : Hopping integral : Excited energy of quasi-particles J. Yu and S. P. Kou, PHYS. REV. B 80, 075107 (2009).
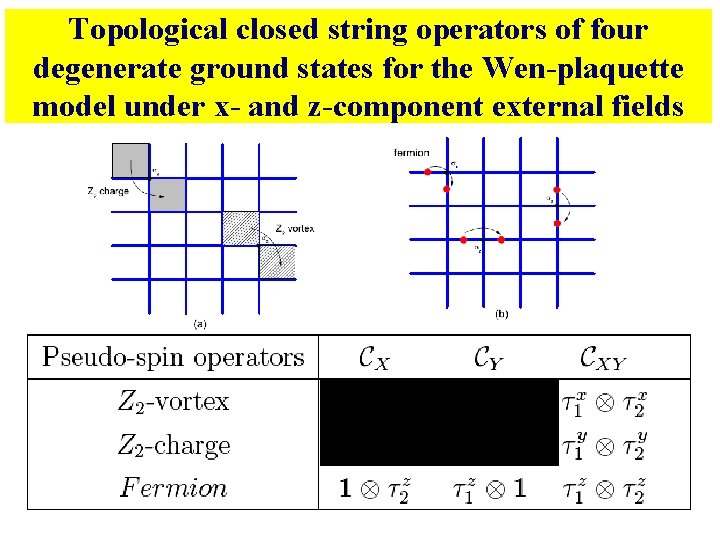
Topological closed string operators of four degenerate ground states for the Wen-plaquette model under x- and z-component external fields

Effective model of four degenerate ground states for the Wen-plaquette model under x- and z-component external fields

External field along z direction • In anisotropy limit, the four degenerate ground states split two groups, 2× 6 lattice on the Wenplaquette model under z direction field

External field along z direction • Isotropy limit, the four degenerate ground states split three groups 4× 4 lattice on Wenplaquette model under zdirection

External field along x direction • Under x-direction field, the four degenerate ground states split three groups: 4× 4 lattice on Wenplaquette model under xdirection
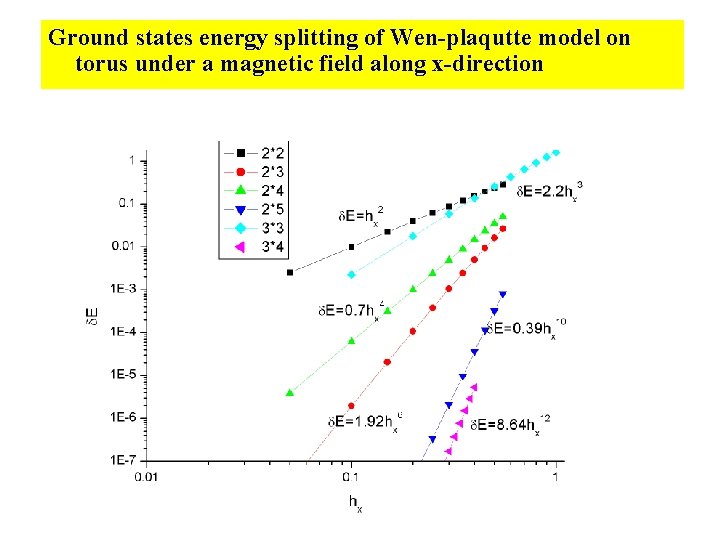
Ground states energy splitting of Wen-plaqutte model on torus under a magnetic field along x-direction
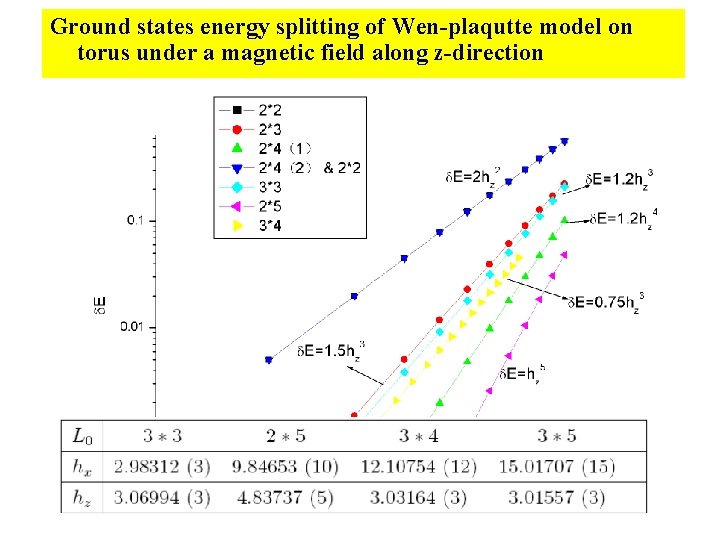
Ground states energy splitting of Wen-plaqutte model on torus under a magnetic field along z-direction
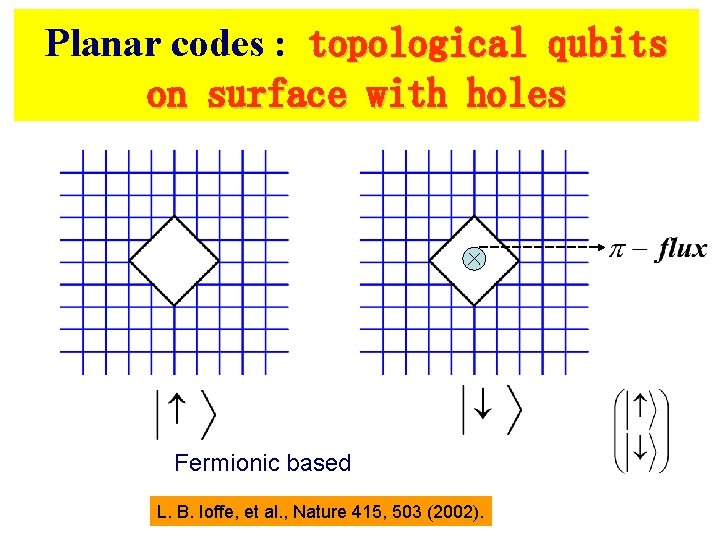
Planar codes : topological qubits on surface with holes Fermionic based L. B. Ioffe, et al. , Nature 415, 503 (2002).
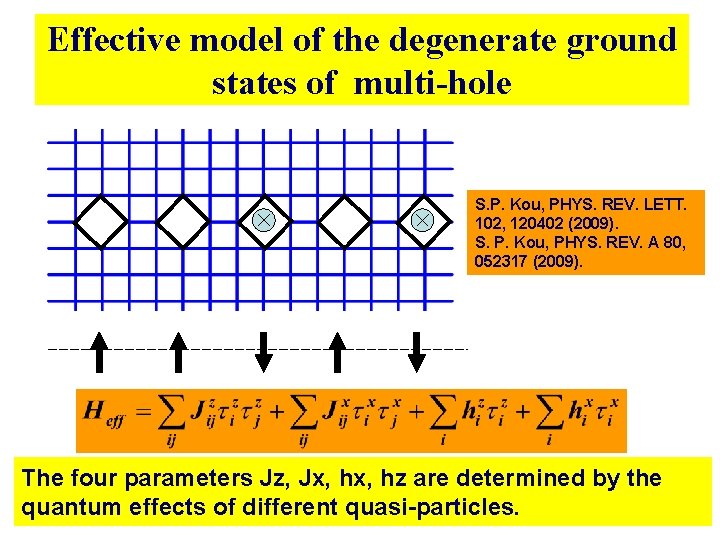
Effective model of the degenerate ground states of multi-hole S. P. Kou, PHYS. REV. LETT. 102, 120402 (2009). S. P. Kou, PHYS. REV. A 80, 052317 (2009). The four parameters Jz, Jx, hz are determined by the quantum effects of different quasi-particles.

Unitary operations • A general operator becomes : For example , Hadamard gate is
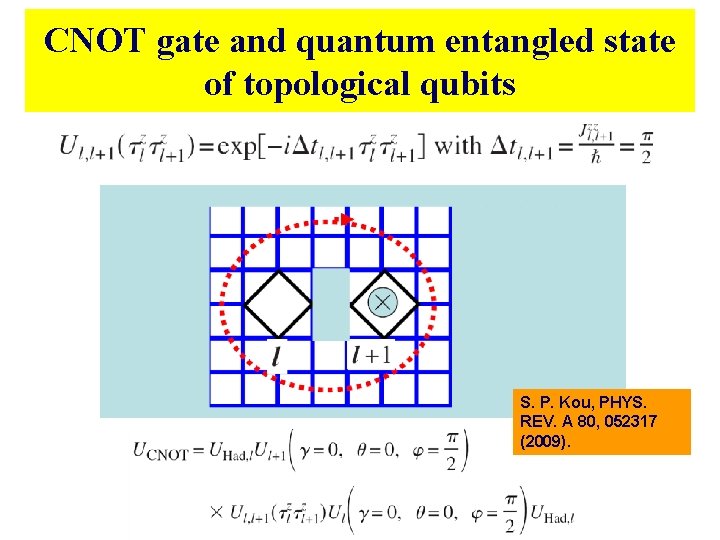
CNOT gate and quantum entangled state of topological qubits S. P. Kou, PHYS. REV. A 80, 052317 (2009).

III. Topological quantum computation by braiding Ising anyons
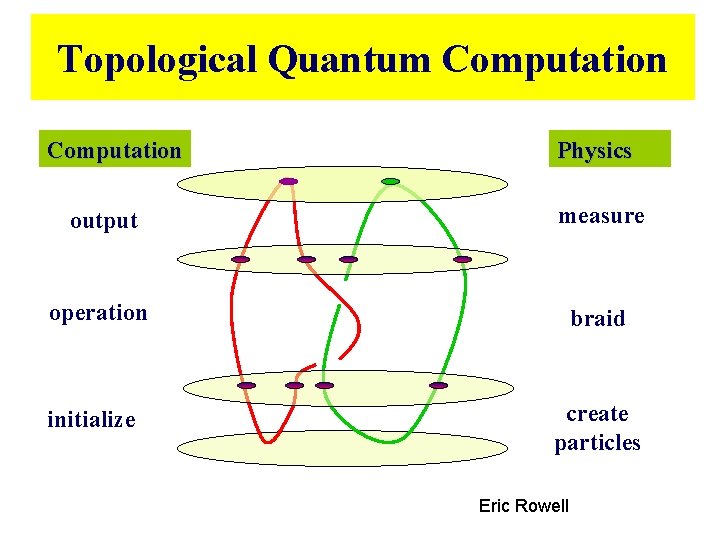
Topological Quantum Computation Physics output measure operation braid initialize create particles Eric Rowell

(I) Ising anyons Fusion rules:
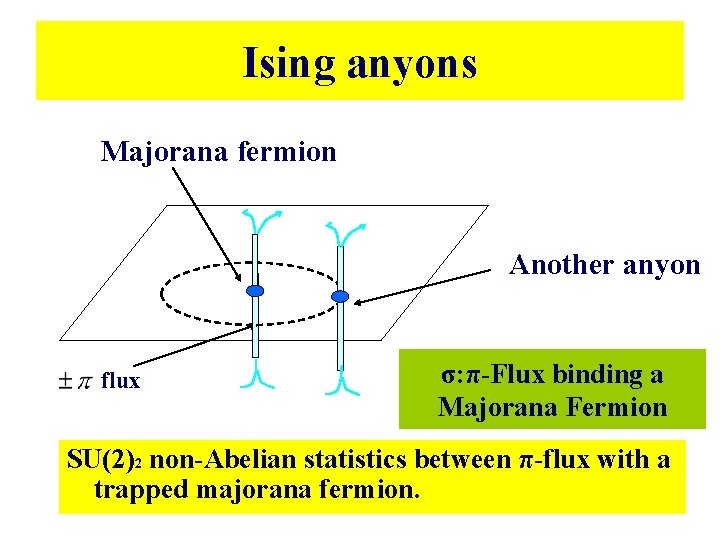
Ising anyons Majorana fermion Another anyon flux σ: π-Flux binding a Majorana Fermion SU(2)2 non-Abelian statistics between π-flux with a trapped majorana fermion.

px+ipy-wave superconductor : an example of symmetry protected topological order • µ>0, non-Abelian Topologial state • µ<0, Abelian Topologial state Read, Green, 2000. S. P. Kou and X. G. Wen, 2009.
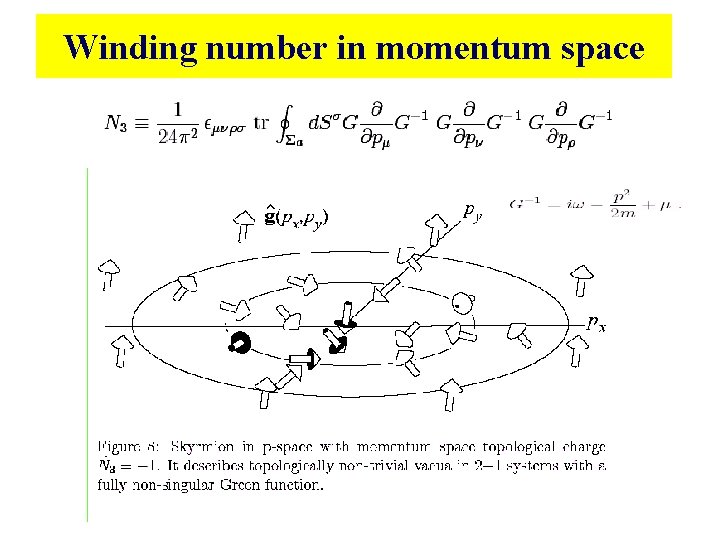
Winding number in momentum space

Bd. G equation of px+ipy superconductor Bogoliubov de. Gennes Hamiltonian: Eigenstates in +/- E pairs Spectrum with a gap Excitations: Fermionic quasiparticles above the gap

Bd. G equation of vortex in px+ipy superconductor E = 0

Whyπ vortex in px+ipy wave superconductors traps majorona fermion? • The existence of zero mode in πflux for chiral superconducting state : cancelation between the π flux of vortex and edge chiral angle (winding numer in momentum space) • Majorana fermion in chiral p-wave – mixed annihilation operator and generation operation
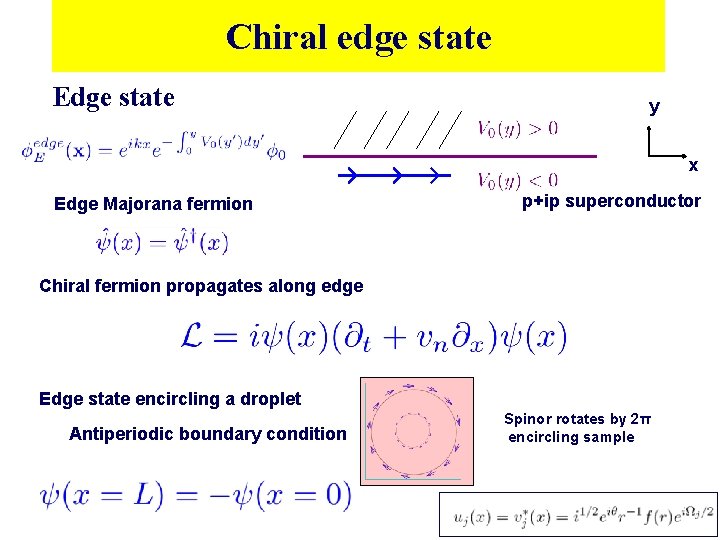
Chiral edge state Edge state y x Edge Majorana fermion p+ip superconductor Chiral fermion propagates along edge Edge state encircling a droplet Antiperiodic boundary condition Spinor rotates by 2π encircling sample

Vortex (πflux) in px+ipy superconductor Single vortex E=0 Majorana fermion encircling sample : an encircling vortex - a “vortex zero mode” Fermion picks up π phase around vortex: Changes to periodic boundary condition

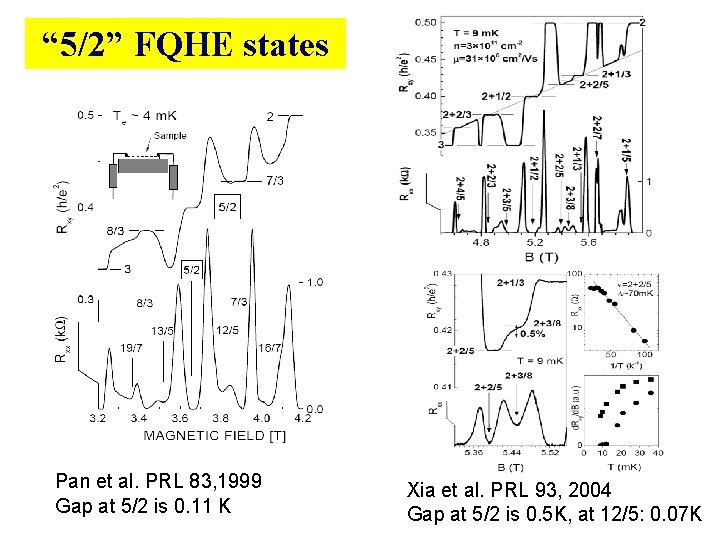
“ 5/2” FQHE states Pan et al. PRL 83, 1999 Gap at 5/2 is 0. 11 K Xia et al. PRL 93, 2004 Gap at 5/2 is 0. 5 K, at 12/5: 0. 07 K

Moore-Read wavefunction for 5/2 FQHE state “Paired” Hall state Pfaffian: Moore, Read (1991) Greiter, Wen, Wilczek (1992)
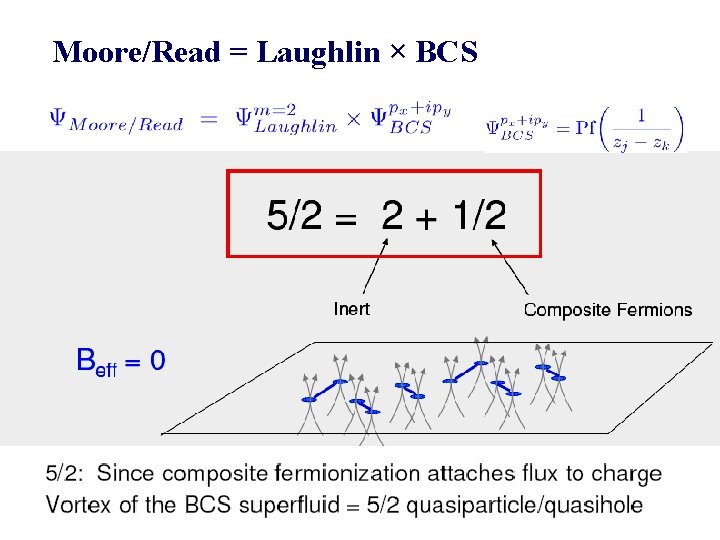
Moore/Read = Laughlin × BCS

Ising anyons in the generalized Kitaev model Gapped B phase are SU(2)2 non. Abelian topological order for K>0. Boundaries: • • • Vortex-free: J=1/2 Full-vortex: J=1/√ 2 Sparse: 1/2 ≤ J ≤ 1/√ 2 (Jz = 1 and J = Jx = Jy )

px+ipy SC for generalized Kitaev model by Jordan-Wigner transformation Y. Yue and Z. Q. Wang, Europhys. Lett. 84, 57002 (2008)

Topological qubits of Ising anyons • Pairs of Ising anyons : each anyon binds to a Majorana fermion, the fermion state of two anyons is described by a regular fermion which is a qubit. A qubit

Braiding operator for two-anyons The braiding matrices are (Ivanov, 2001) :

Braiding matrices for the degenerate states of four Ising anyons Two- qubit

N matrices F matrices R matrices
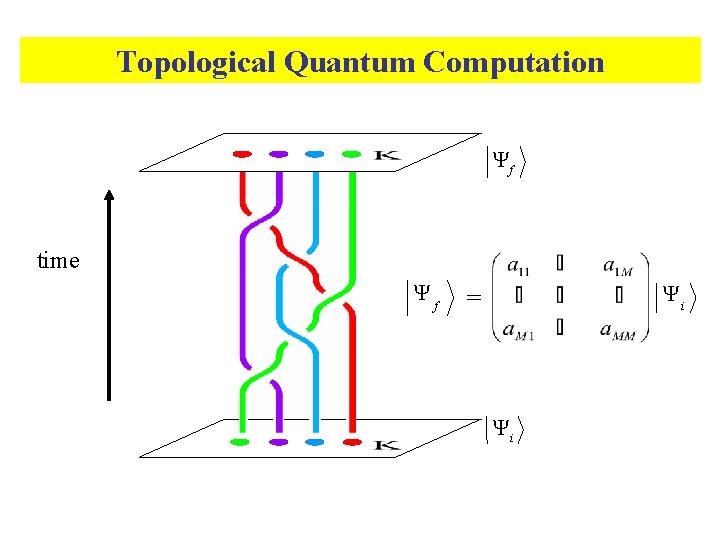
Topological Quantum Computation Yf time Yf Yi = Yi

Topological quantum computation by Ising anyons • Two pairs of Ising anyons R matrices of two pairs of anyons : braiding operators
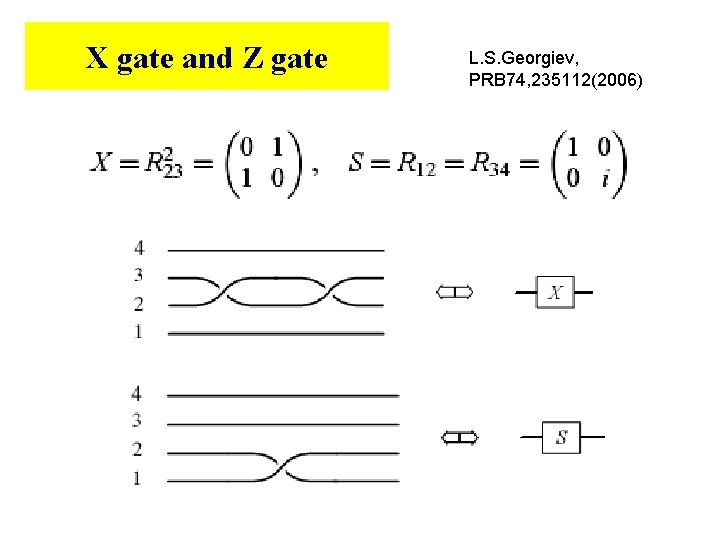
X gate and Z gate L. S. Georgiev, PRB 74, 235112(2006)
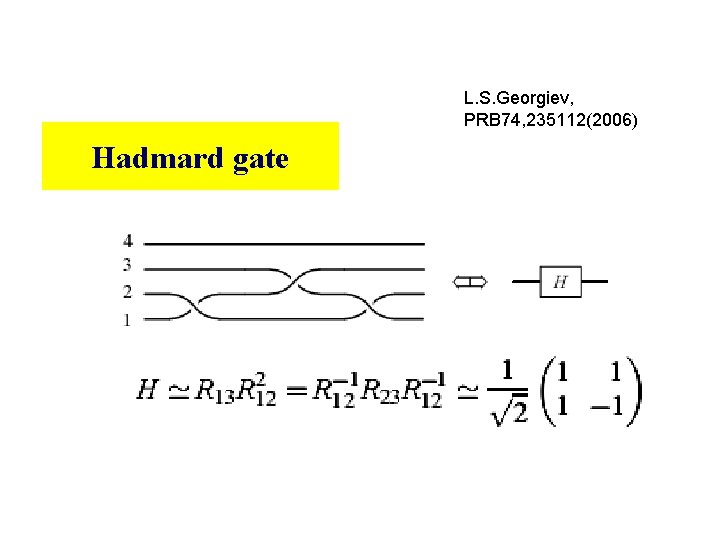
L. S. Georgiev, PRB 74, 235112(2006) Hadmard gate
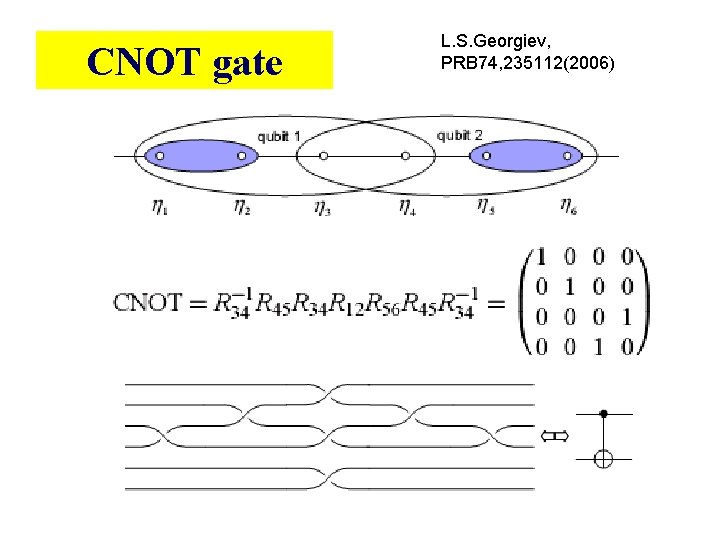
CNOT gate L. S. Georgiev, PRB 74, 235112(2006)
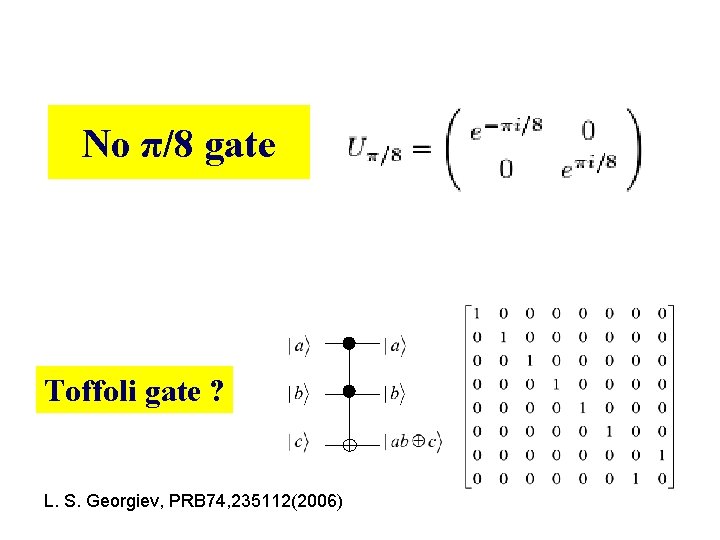
No π/8 gate Toffoli gate ? L. S. Georgiev, PRB 74, 235112(2006)

IV. Topological quantum computation by braiding Fibonacci anyons

(2) Fibonacci anyon There are two sectors : I and τ. Two anyons (τ) can “fuse” two ways. Fusion rules

Fibonacci anyon • Fib(n) = Fib(n– 1) + Fib(n– 2)

Fibonacci anyons =1, 2, 3, 5, 8, 13, 21, 34, 55, …

Fibonacci anyon N matrices F matrices R matrices

Other examples of Fibonacci anyon
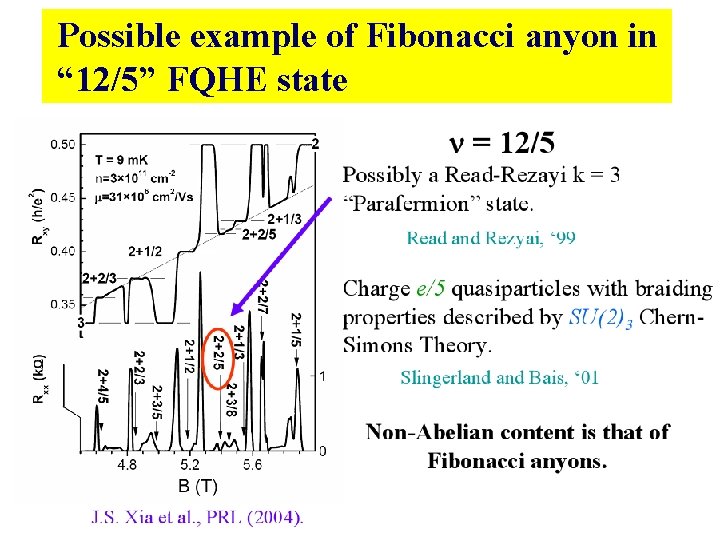
Possible example of Fibonacci anyon in “ 12/5” FQHE state

Read-Rezayi wave-function Para-fermion state : bound state of three fermions N. Read and E. H. Rezayi, Phys. Rev. B 59, 8084 (1999).
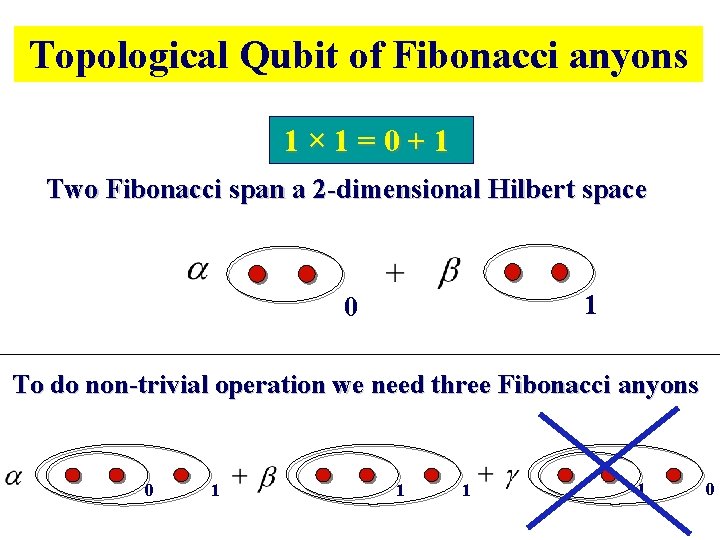
Topological Qubit of Fibonacci anyons 1 × 1 = 0 + 1 Two Fibonacci span a 2 -dimensional Hilbert space 1 0 To do non-trivial operation we need three Fibonacci anyons 0 1 1 0
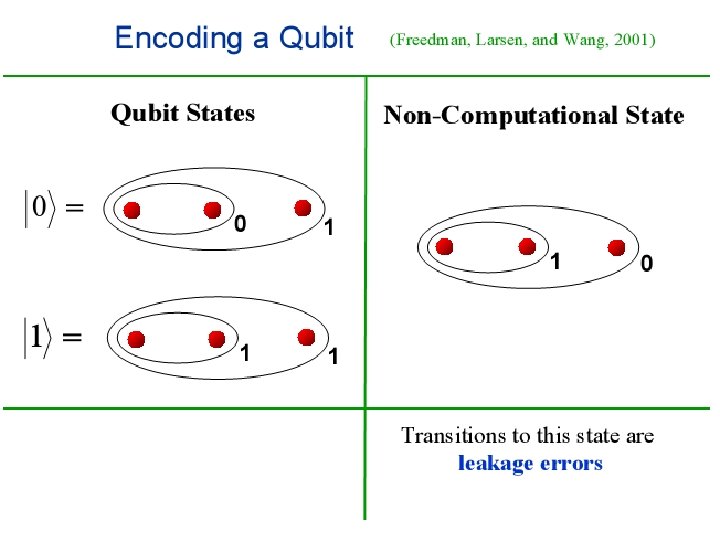

P. Bonderson et. al
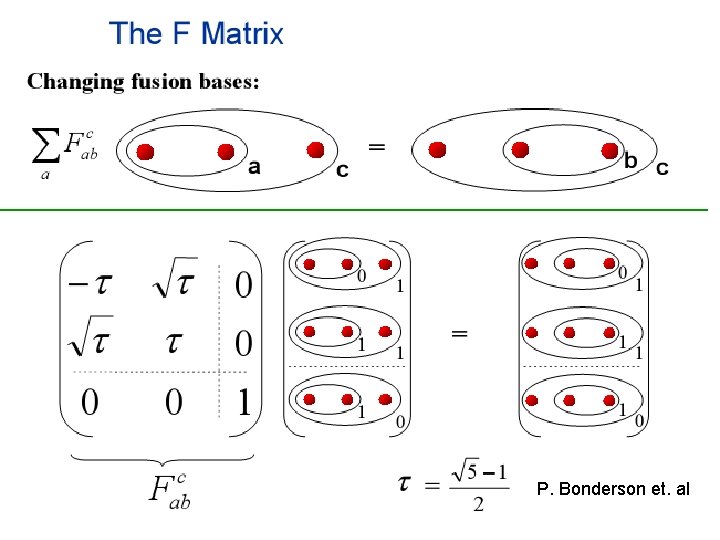
P. Bonderson et. al
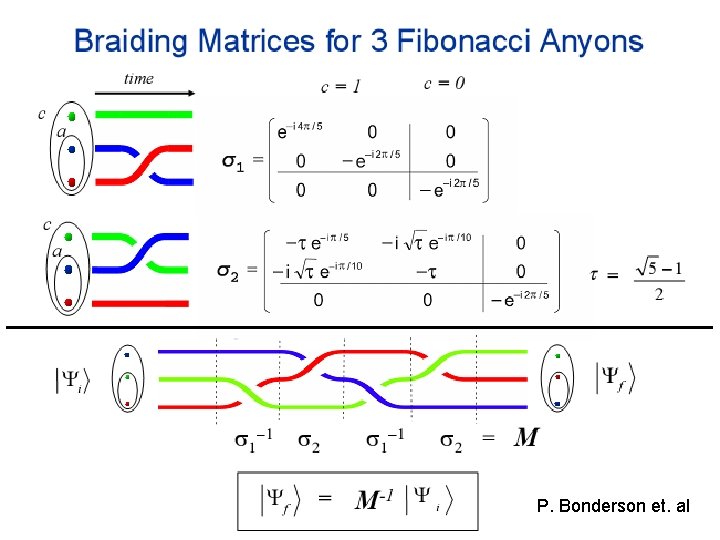
P. Bonderson et. al
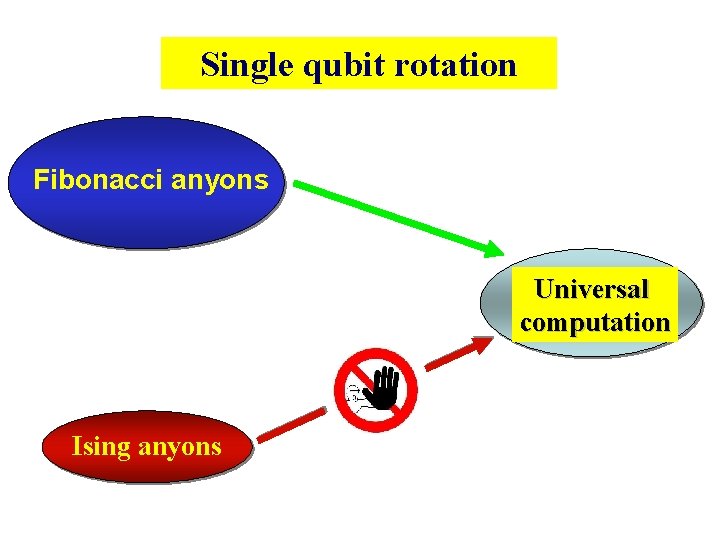
Single qubit rotation Fibonacci anyons Universal computation Ising anyons
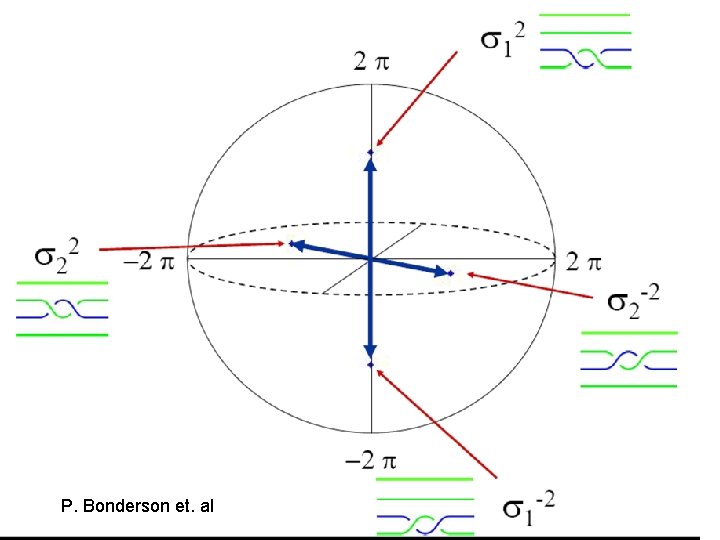
P. Bonderson et. al
P. Bonderson et. al
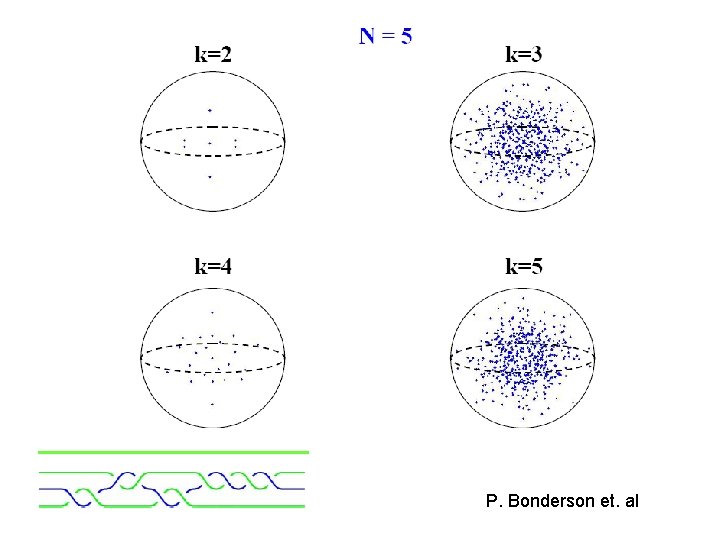
P. Bonderson et. al
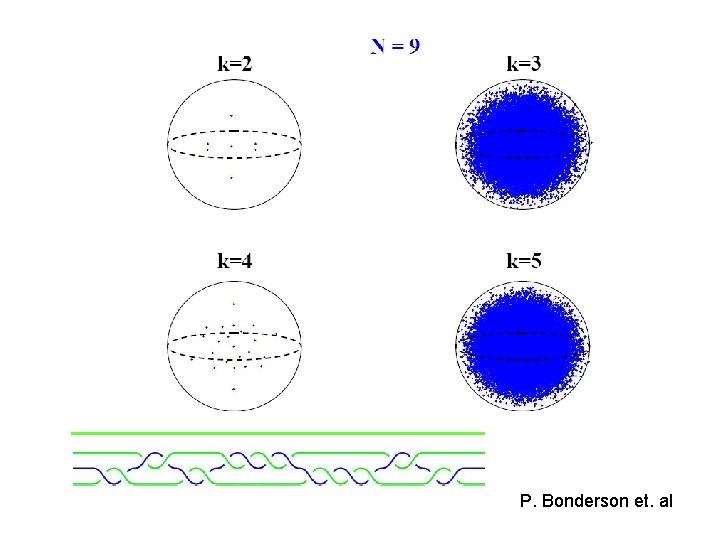
P. Bonderson et. al

P. Bonderson et. al
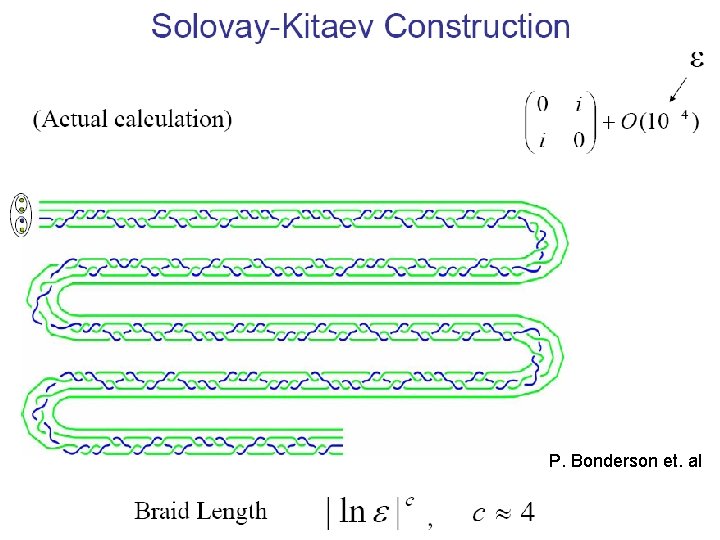
P. Bonderson et. al
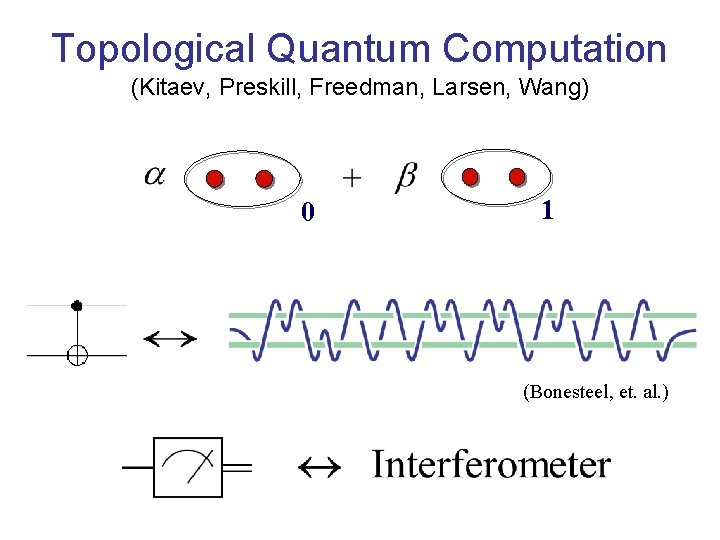
Topological Quantum Computation (Kitaev, Preskill, Freedman, Larsen, Wang) 0 1 (Bonesteel, et. al. )

P. Bonderson et. al

Thank you!
- Slides: 106