Anvendt Statistik Lektion 8 Multipel Liner Regression 1

Anvendt Statistik Lektion 8 Multipel Lineær Regression 1

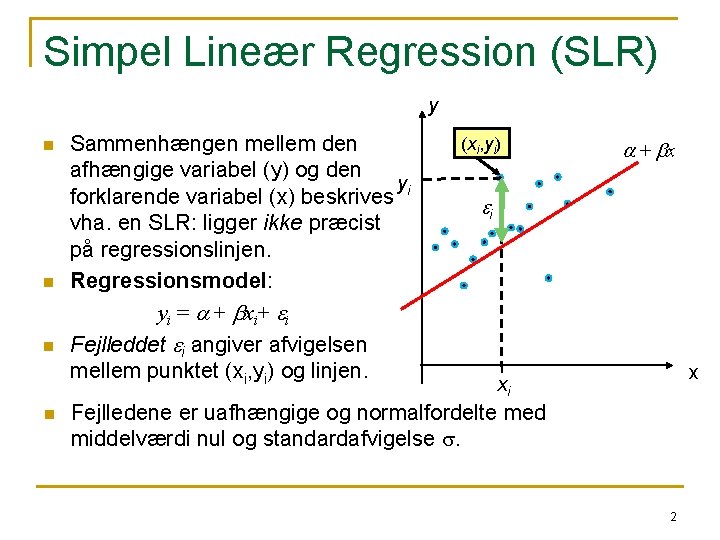
Simpel Lineær Regression (SLR) y n n Sammenhængen mellem den afhængige variabel (y) og den y forklarende variabel (x) beskrives i vha. en SLR: ligger ikke præcist på regressionslinjen. Regressionsmodel: y i = a + b x i+ e i Fejlleddet ei angiver afvigelsen mellem punktet (xi, yi) og linjen. (xi, yi) a + bx ei x xi Fejlledene er uafhængige og normalfordelte med middelværdi nul og standardafvigelse s. 2

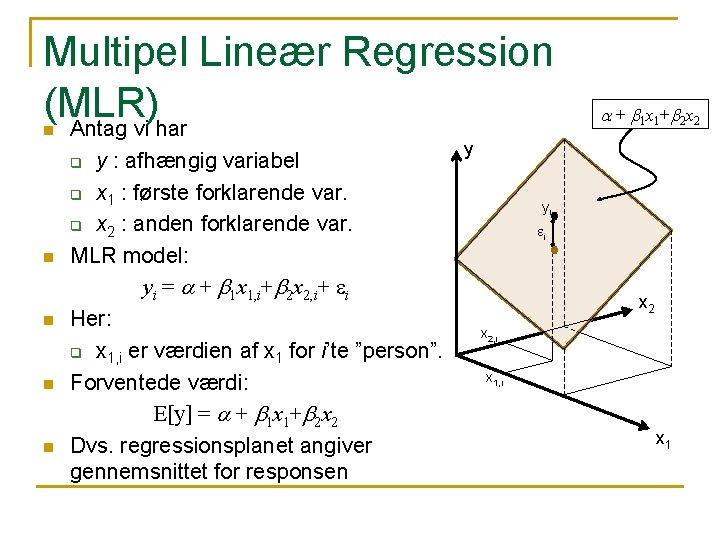
Multipel Lineær Regression (MLR) Antag vi har n y : afhængig variabel q x 1 : første forklarende var. q x 2 : anden forklarende var. MLR model: yi = a + b 1 x 1, i+b 2 x 2, i+ ei Her: q x 1, i er værdien af x 1 for i’te ”person”. Forventede værdi: E[y] = a + b 1 x 1+b 2 x 2 Dvs. regressionsplanet angiver gennemsnittet for responsen q n n a + b 1 x 1 +b 2 x 2 y yi ei x 2, i x 1

Fortolkning af bj n n Antag vi har k forklarende variable: yi = a + b 1 x 1, i+b 2 x 2, i+ ··· +bkxk, i + ei Fortolkningen af bj: q Hvis f. eks. x 1 øges med 1, så øges den forventede værdi af y med b 1, hvis x 2, x 3, …, xk forbliver uændrede (og fortolkningen er naturligvis tilsvarende for b 2, b 3 , …, bk).

Prædiktion og Residual n MLR model: yi = a + b 1 x 1, i+b 2 x 2, i+ ··· +bkxk, i +ei n Prædiktionsligningen er n Dvs. n Residual: Dvs. residualet er et estimat af ei. n er et estimat af E[yi].

Mindste kvadraters metode n Definer summen af de kvadrerede residualer n UK: Sum of Squared Errors SPSS: Sum of Squared Residuals n n Mindste kvadraters metode: q Vi vælger a, b 1, b 2, …, bk, så SSE er mindst mulig. q Bemærk at

Eksempel: Kriminalitet i Florida n Tre variable q y : crime rate (kriminalitetsrate) q x 1: education (uddannelse) q x 2: urbanization (urbanisering) n I første omgang: Kriminalitetsrate og uddannelse

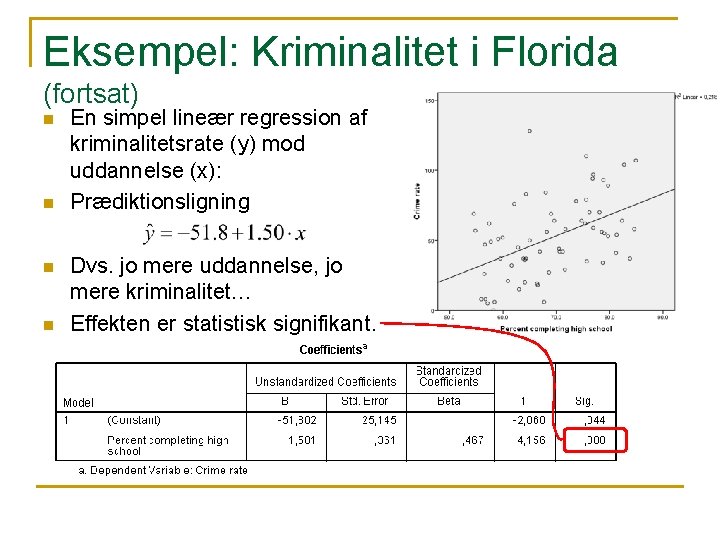
Eksempel: Kriminalitet i Florida (fortsat) n n En simpel lineær regression af kriminalitetsrate (y) mod uddannelse (x): Prædiktionsligning Dvs. jo mere uddannelse, jo mere kriminalitet… Effekten er statistisk signifikant.

Eksempel: Kriminalitet i Florida (fortsat) n n Teori: Jo mere urbaniseret, jo mere kriminalitet og jo flere med lang uddannelse. Multipel lineær regression af kriminalitetsrate (y) mod både uddannelse (x 1) og urbanisering (x 2). Prædiktionsligning: Crime rate Urbanization Education Bemærk at effekten af uddannelse nu er negativ og ikke længere er signifikant (P-værdi >> 5%).

Eksempel: Kriminalitet i Florida (fortsat) n Prædiktionsligning: n Effekten af x 1 (uddannelse) er den samme for alle værdier af x 2 (ubanisering). For hver ekstra procent-point uddannede falder kriminalitetsraten med 0. 54. Bemærk at effekten af x 1 (uddannelse) ændrede sig markant, da vi tilføjede x 2 (urbanisering). Det tyder på at der er en stærk sammenhæng mellem x 1 og x 2. n n

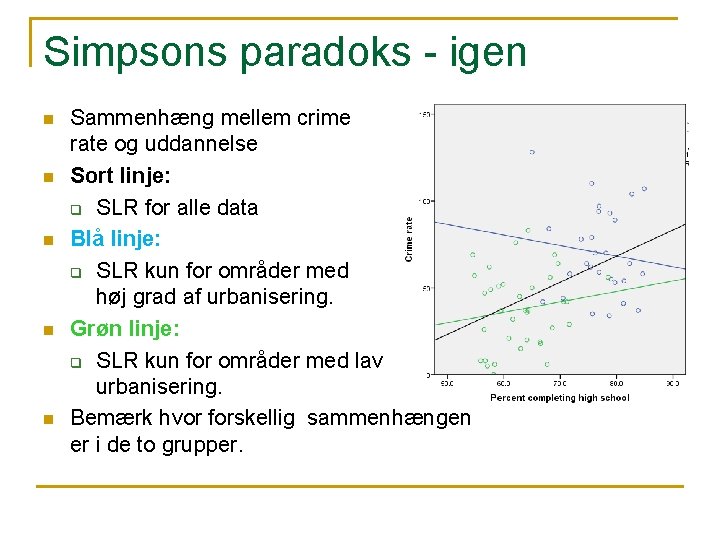
Simpsons paradoks - igen n n Sammenhæng mellem crime rate og uddannelse Sort linje: q SLR for alle data Blå linje: q SLR kun for områder med høj grad af urbanisering. Grøn linje: q SLR kun for områder med lav urbanisering. Bemærk hvor forskellig sammenhængen er i de to grupper.

Eksempel: Mentalt helbred n Vi har tre variable: q y : Mental impairment (funktionsnedsættelse), afhængig var. q x 1 : Life events, første forklarende variabel. q x 2 : Socioøkonomisk status (SES), anden forklarende var. n Multipel lineær regressionsmodel: yi = a + b 1 x 1, i+b 2 x 2, i+ei n MLR antager en lineær sammenhæng mellem y og hvert xj. Vi starter med et scatter plot for hvert par af variable. n

Scatterplot Matrix n Graphs → Chart builder → Scatter/Dot →Scatterplot Matrix n Ingen åbenlyse ikke-lineære sammenhænge. Ingen åbenbare sammenhænge i det hele taget… n n n Problem: Plot viser sammenhængen mellem y og fx. x 1, hvor vi ignorer værdien af x 2. Vi har set, at vi ikke kan ignorere effekten af x 2, når vi ser på sammenhængen mellem y og x 1.

Partielt plot n Estimeret model (eksempel med tre forklarende variable) n Estimeret del-model (uden x 1) n Regression af x 1 mod x 2 og x 3 (hvordan afhænger x 1 af x 2 og x 3) n Vi har to sæt residualer: Ide: plot mod. n (for y) og (for x 1).

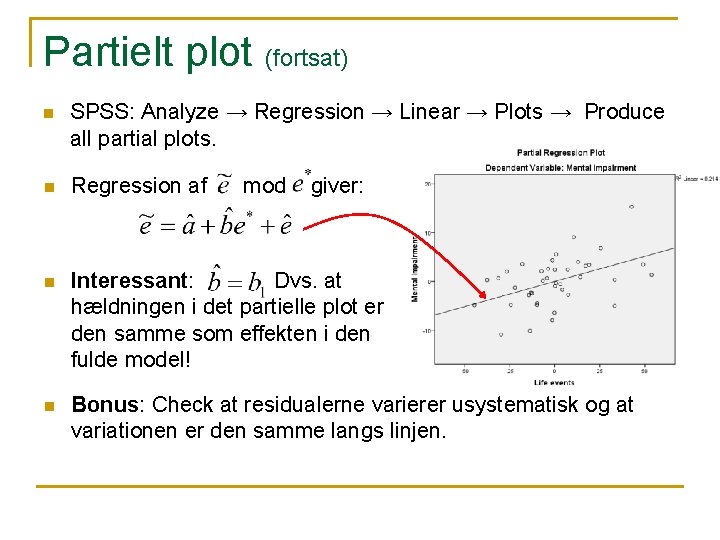
Partielt plot (fortsat) n SPSS: Analyze → Regression → Linear → Plots → Produce all partial plots. n Regression af n Interessant: Dvs. at hældningen i det partielle plot er den samme som effekten i den fulde model! n Bonus: Check at residualerne varierer usystematisk og at variationen er den samme langs linjen. mod giver:

SPSS output n Simpel model – kun en forklarende variabel n Model med to forklarende variable:

Multipel korrelation n Husk: Korrelation angiver hvor lineært afhængig to variable er. n Multipel korrelation R for en lineær regression er korrelationen mellem de observerede og de prædikterede. n Bemærk: Den multiple korrelation kan ikke være negativ.

Multipel determinationskoefficient n Den totale variation i y’erne: (Total Sum of Squares) n Den uforklarede del af variationen i y’erne: (Sum of Squared Errors) n Den forklarede del af variationen i y’erne: n Multipel determinationskoefficient n Fortolkning: Andelen af den totale variation, der er forklaret.

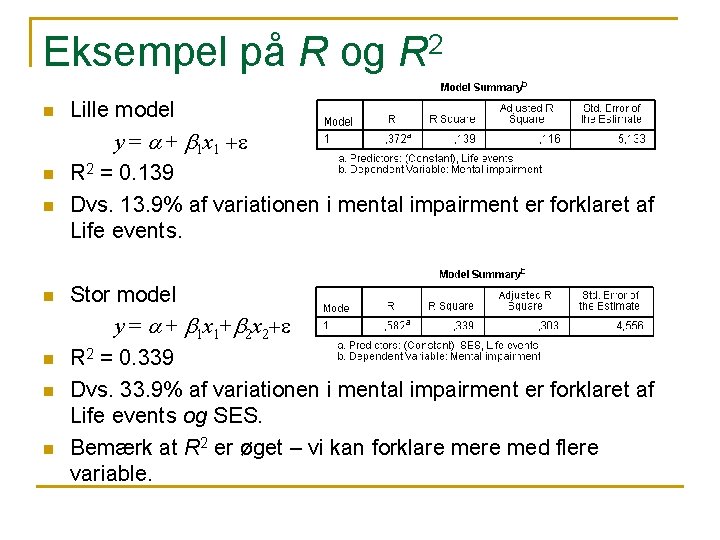
Eksempel på R og R 2 n n n n Lille model y = a + b 1 x 1 +e R 2 = 0. 139 Dvs. 13. 9% af variationen i mental impairment er forklaret af Life events. Stor model y = a + b 1 x 1+b 2 x 2+e R 2 = 0. 339 Dvs. 33. 9% af variationen i mental impairment er forklaret af Life events og SES. Bemærk at R 2 er øget – vi kan forklare med flere variable.

Egenskaber for R og R 2 n n n R 2 er mellem 0 og 1 Jo højere R 2, jo bedre kan modellen prædiktere y. R 2 = 1 betyder at y^ = y og alle residualer er nul. R 2 = 0 betyder at b 1 = b 2 = … = bk = 0. Når en variabel tilføjes modellen kan R 2 ikke falde.

Hypotesetest for MLR: F-test n n n MLR model: y = a + b 1 x 1+b 2 x 2+ ··· +bkxk +e Er der mindst en af xj’erne der har en lineær sammenhæng med y? Nul-hypotese: y har ingen lineær sammenhæng med et eneste xj. q H 0: b 1 = b 2 = … = b k = 0 Alternativ-hypotese: y har en lineær sammenhæng med mindst et af xj’erne. q Ha: Mindst et bj 0 Teststørrelse: q

F-testet n n n Hvis H 0 er sand, så følger F en Ffordeling. Som c 2 -fordelingen kan Ffordelingen kun tage positive værdier. Faconen på F-fordelingen er bestemt af to sæt frihedsgrader df 1 og df 2: q q P-værdi Obsereveret F df 1 = k = antal forklarende variable. df 2 = n – (k + 1) = n – antal parametre i modellen

F-test: Eksempel n Model for mentalt helbred: y = a + b 1 x 1 + b 2 x 2 + e n n Fra SPSS har vi R 2 = 0. 339 Dvs. F-fordeling med hhv. 2 og 47 frihedsgrader P-værdi 9. 49 n n P-værdien finder vi vha. SPSS (næste slide). Da P-værdien < 0. 0005 afviser vi H 0, dvs. y har en lineær sammenhæng med mindst en af de to forklarende variable.

F-test i SPSS n F-teststørrelsen kan omskrives: P-værdi SSE TSS

Hypotesetest af bj n n n MLR model: y = a + b 1 x 1+b 2 x 2+ ··· +bkxk +e Er der en lineær sammenhæng mellem y og xj? Nul-hypotese: y har ingen lineær sammenhæng med xj. q H 0: b j = 0 Alternativ-hypotese: y har en lineær sammenhæng med xj. q H a: b j 0 Teststørrelse: q n Udregnes af SPSS Hvis H 0 er sand, så følger t en t-fordeling med df = n-(k+1)

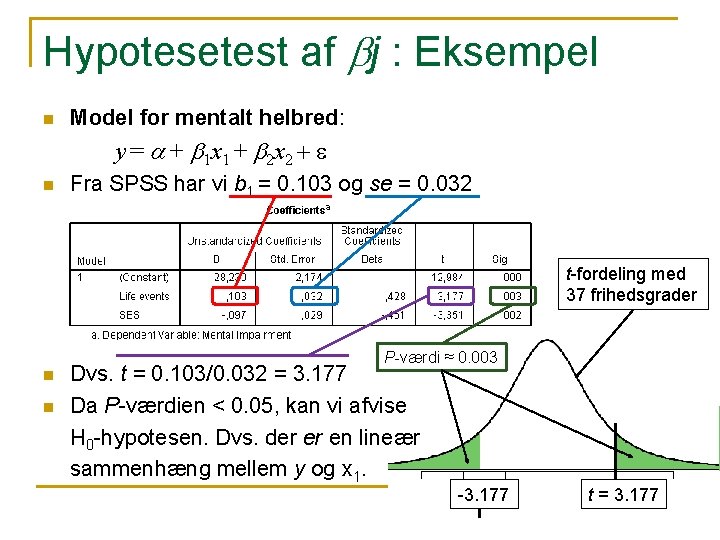
Hypotesetest af bj : Eksempel n Model for mentalt helbred: y = a + b 1 x 1 + b 2 x 2 + e n Fra SPSS har vi b 1 = 0. 103 og se = 0. 032 t-fordeling med 37 frihedsgrader P-værdi ≈ 0. 003 n n Dvs. t = 0. 103/0. 032 = 3. 177 Da P-værdien < 0. 05, kan vi afvise H 0 -hypotesen. Dvs. der er en lineær sammenhæng mellem y og x 1. -3. 177 t = 3. 177

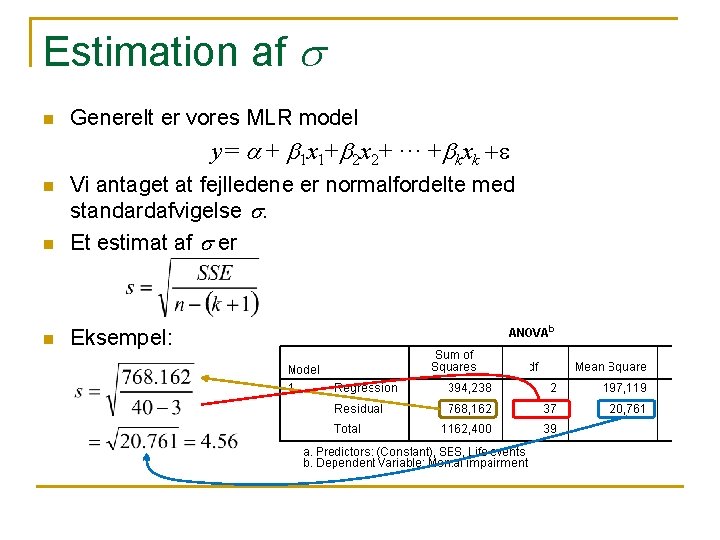
Estimation af s n Generelt er vores MLR model y = a + b 1 x 1+b 2 x 2+ ··· +bkxk +e n Vi antaget at fejlledene er normalfordelte med standardafvigelse s. Et estimat af s er n Eksempel: n

Vekselvirkning n Der er vekselvirkning (også kaldet interaktion) mellem to forklarende variable, x 1 og x 2, for y, hvis effekten af x 1 på y ændrer sig når x 2 ændrer sig. n Simpel vekselvirkningsmodel: y = a + b 1 x 1 + b 2 x 2 + b 3 x 1 x 2 + e n n Hvor kommer interaktionen ind i billedet? Omskriv modellen til y = (a + b 2 x 2) + (b 1+ b 3 x 2) x 1 + e n Bemærk: Hældningen er b 1+ b 3 x 2, dvs. effekten af x 1 på y ændrer sig, når x 2 ændres.

Vekselvirkning: Eksempel n Simpel vekselvirkningsmodel: y = a + b 1 x 1 + b 2 x 2 + b 3 x 1 x 2 + e n n Vha. Transform → Compute variable skaber vi variablen x 1 x 2 = x 1*x 2 Følgende test viser at interaktionen ikke er signifikant: Da vekselvirkningen ikke er signifikant, kan man vælge at fjerne den. Hvis vekselvirkningen er signifikant, beholder vi det. Desuden giver det ikke mening at teste de enkelte led (x 1 og x 2).

Vekselvirkning: Eksempel (fortsat) n n n Estimeret vekselvirkningsmodel: y = 26. 037 + 0. 156·x 1 – 0. 060·x 2 – 0. 01· x 1·x 2 Fortolkning: Når vi øger x 2, så n Reduceres skæringspunktet n Reduceres hældningen.