Anvendt Statistik Lektion 7 Simpel Liner Regression 1

Anvendt Statistik Lektion 7 Simpel Lineær Regression 1

Er der en sammenhæng? n Plot af mordraten (y) mod fattigdomsraten (x): Scatterplot n Er der en sammenhæng? 2

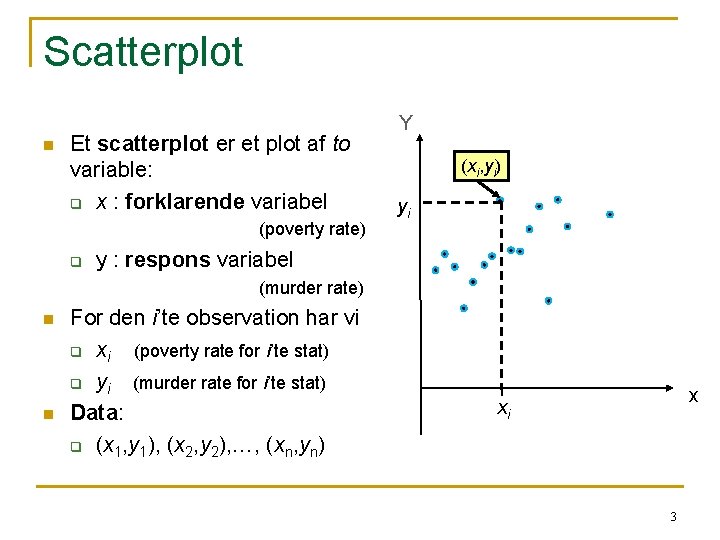
Scatterplot n Et scatterplot er et plot af to variable: q x : forklarende variabel (poverty rate) q Y (xi, yi) yi y : respons variabel (murder rate) n n For den i’te observation har vi q xi (poverty rate for i’te stat) q yi (murder rate for i’te stat) Data: q (x 1, y 1), (x 2, y 2), …, (xn, yn) x xi 3

Forventet respons: En ret linje Den rette linje a + bx beskriver den forventede (dvs. middel) respons: y UK: Expected E[y] = a + bx n Eksempel: E[y] = 210 + 25 x n Fortolkning: q Antag x = 4 (poverty rate), så er den forventede y (murder rate) 210 + 25· 4 = 310 a q Hvis x øges med 1, så øges den forventede værdi af y med 25. n E[y] = a + bx b 1 x q Hvis x = 0 , så er den forventede værdi af y = 210. 4

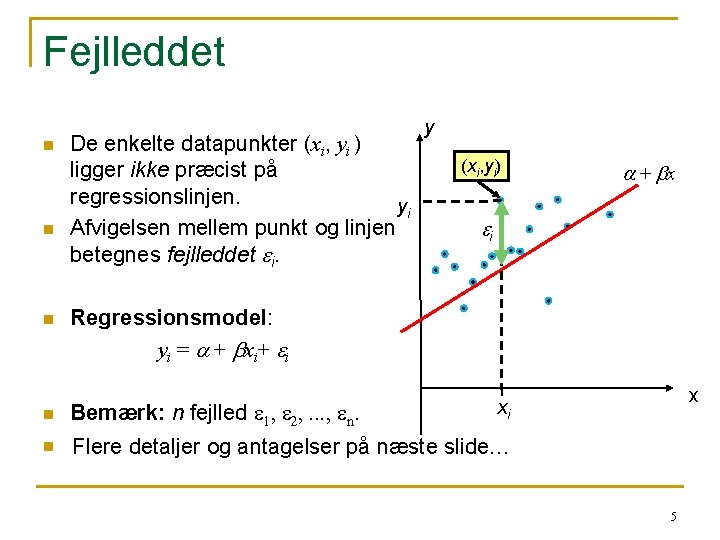
Fejlleddet n n n De enkelte datapunkter (xi, yi ) ligger ikke præcist på regressionslinjen. yi Afvigelsen mellem punkt og linjen betegnes fejlleddet ei. y (xi, yi) a + bx ei Regressionsmodel: y i = a + b x i+ e i x xi n Bemærk: n fejlled e 1, e 2, . . . , en. n Flere detaljer og antagelser på næste slide… 5

Simpel lineær regressionsmodel • y • x • a • β • iid • εi - den afhængige variabel. - den uafhængige variabel – faste - skæringspunkt med y-aksen - hældningskoefficient - UK: independent, identically distributed = uafhængig, identisk fordelte - det græske bogstav ”epsilon” - det eneste stokastiske element i modellen 6

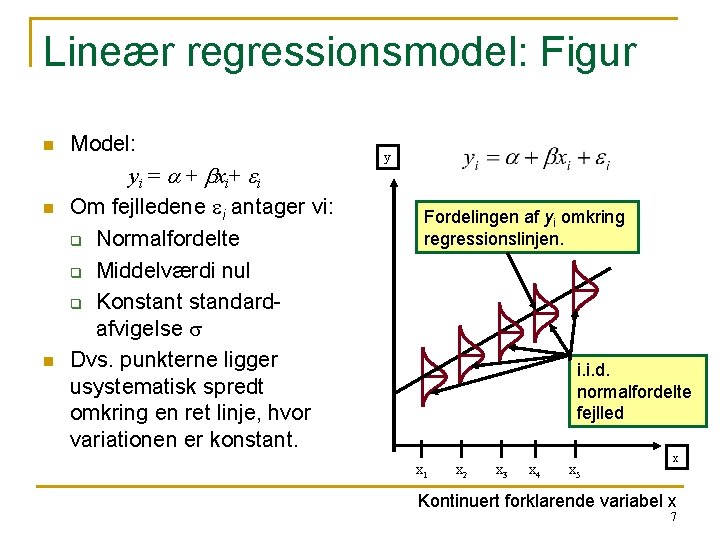
Lineær regressionsmodel: Figur n n n Model: y i = a + b x i+ e i Om fejlledene ei antager vi: q Normalfordelte q Middelværdi nul q Konstant standardafvigelse s Dvs. punkterne ligger usystematisk spredt omkring en ret linje, hvor variationen er konstant. y Fordelingen af yi omkring regressionslinjen. i. i. d. normalfordelte fejlled x 1 x 2 x 3 x 4 x 5 x Kontinuert forklarende variabel x 7

Forudsætninger for SLR (1/3) n n Der er en lineær sammenhæng mellem x og y. Indledende tjek: Scatter plot af (x, y) – ser punkterne ud til at ligge langs en ret linje? y y x 8

Forudsætninger for SLR (2/3) n n Værdierne af de uafhængige variable x antages at være faste – dvs. ikke stokastiske. Mao. Antages x at være kendt eller målt uden ”støj”/”målefejl” Indledende tjek: Logisk sans. 9

Forudsætninger for SLR (3/3) n n Fejledene εi antages være uafhængige og normalfordelte med middelværdi 0 og konstant standardafvigelse σ. Indledende tjek: Se efter indlysende problemer i scatter plot af (x, y). y y x 10

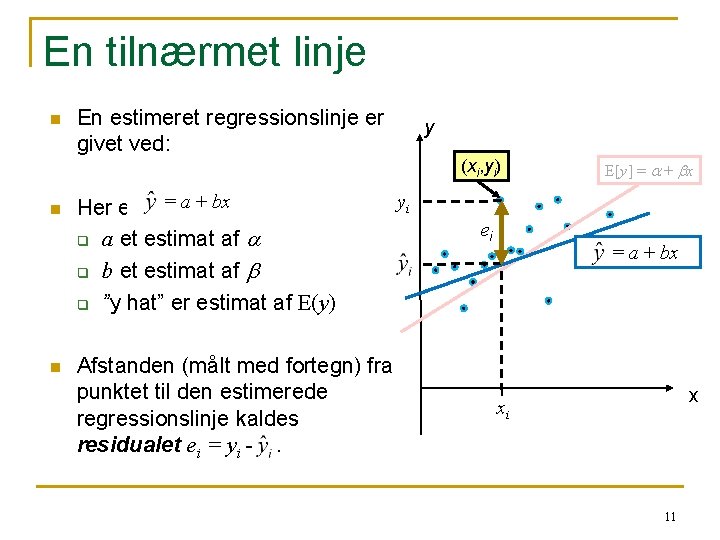
En tilnærmet linje n En estimeret regressionslinje er givet ved: y (xi, yi) n n Her er = a + bx q a et estimat af a q b et estimat af b q ”y hat” er estimat af E(y) Afstanden (målt med fortegn) fra punktet til den estimerede regressionslinje kaldes residualet ei = yi -. E[y] = a + bx yi ei = a + bx x xi 11

Mindste kvadraters metode n y Summen af de kvadrerede residualer betegnes: (xi, yi) E[y] = a + bx yi ei n UK: Sum of Squared Errors. n SSE kan skrives som n n Vi vælger a og b, så SSE er mindst mulig. Dette kaldes mindste kvadraters metode. = a + bx x xi 12

Estimater af a , b og s n Mindste kvadraters metode giver følgende estimater Estimatet for b er n Estimatet for a er n Estimatet for s er n 13

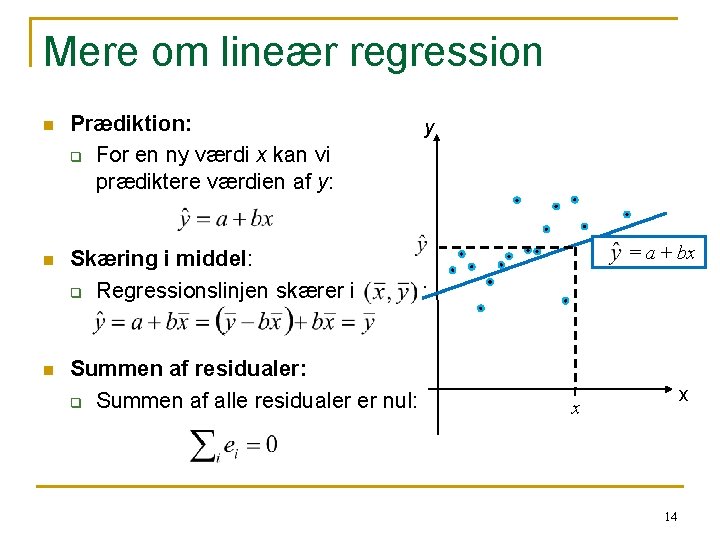
Mere om lineær regression n Prædiktion: q For en ny værdi x kan vi prædiktere værdien af y: n Skæring i middel: q Regressionslinjen skærer i n Summen af residualer: q Summen af alle residualer er nul: y = a + bx : x x 14

Simpel lineær regression i SPSS n Anazyze → Regression → Linear y x 15

SPSS: Resultat a b n Den estimerede regressionslinje er altså: = -10, 136 + 1, 323 x n Fortolkning n Hver gang andelen af fattige stiger en procent stiger den forventede mordrate med 1, 323 mord pr 100. 000. n Hvis der er nul procent fattige, så er den forventede mordrate -10, 136… n Hvis fattigdomsprocenten er 16. 2, så er den prædikterede mordrate: -10. 136 + 1. 323· 16. 2 = 11. 30. 16

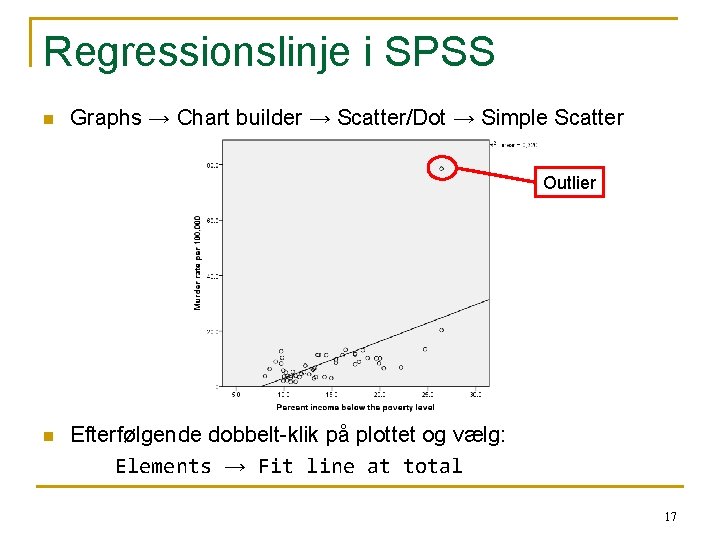
Regressionslinje i SPSS n Graphs → Chart builder → Scatter/Dot → Simple Scatter Outlier n Efterfølgende dobbelt-klik på plottet og vælg: Elements → Fit line at total 17

Estimat af s n Simpel lineær regression i SPSS giver også følgende resultater: SSE n n n-2 SSE/(n-2) Estimat af s : Dvs. vi forventer at ca. 95% af punkterne ligger højst 2· 8. 9 enheder fra regressionslinjen. 18

Hypotesetest af b n n n Nul-hypotese: q H 0: b = 0 Alternativ-hypoteser: q H a: b 0 H a: b > 0 Teststørrelse q H a: b < 0 Hvis H 0 er sand, så følger t en tfordeling med df=n-2 frihedsgrader hvor se er standardfejlen: , hvor 19

Fortolkning af H 0: β = 0 Er der en lineær sammenhæng mellem x og y? H 0: β = 0 H a: β ≠ 0 ingen lineær sammenhæng Følgende er eksempler, hvor H 0 ikke afvises. Konstant Y Usystematisk variation Y Y X Ikke-lineær sammenhæng Y X X 20

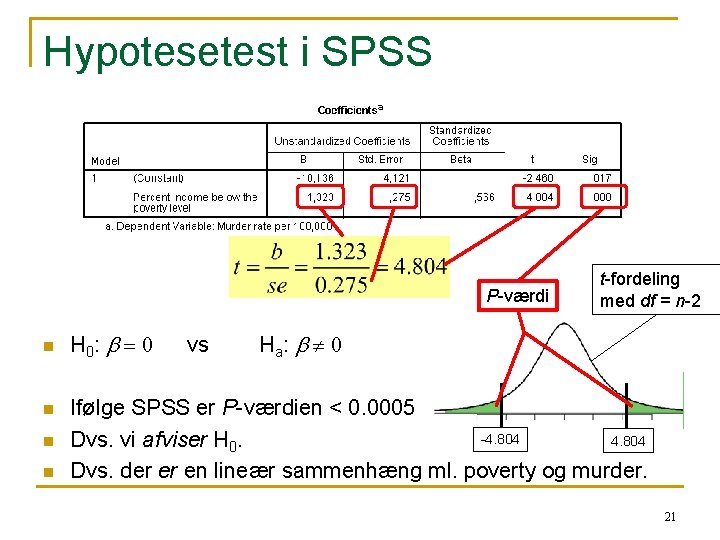
Hypotesetest i SPSS P-værdi n n H 0: b = 0 vs t-fordeling med df = n-2 H a: b 0 Ifølge SPSS er P-værdien < 0. 0005 -4. 804 Dvs. vi afviser H 0. Dvs. der er en lineær sammenhæng ml. poverty og murder. 21

Konfidensintervaller for b n Konfidensintervallet for b følger det sædvanlige mønster: b ± tn-2, a/2 · se n Standardfejlen se udregnes som før, og udregnes i praksis af SPSS. n I dialogboksen for lineær regression tilvælges konfidensintervaller under ’statistics’ n 95% konf. int. : 1. 323 ± 2. 01 · 0. 275 = [ 0. 770 ; 1. 876 ] t 49, 0. 025 = 2. 01 22

Korrelationen r n n Graden af lineær sammenhæng mellem x og y kan måles ved korrelationen r. Standardafvigelsen for hhv. x og y er: og n Korrelationen kan udregnes som 23

Korrelationen: Egenskaber n Egenskaber ved korrelationen: q -1 ≤ r ≤ 1 q r har samme fortegn som b q r = 0 : ingen lineær sammenhæng q r = ± 1 : perfekt lineær sammenhæng q Jo større absolut værdi, jo stærkere lineær sammenhæng 24

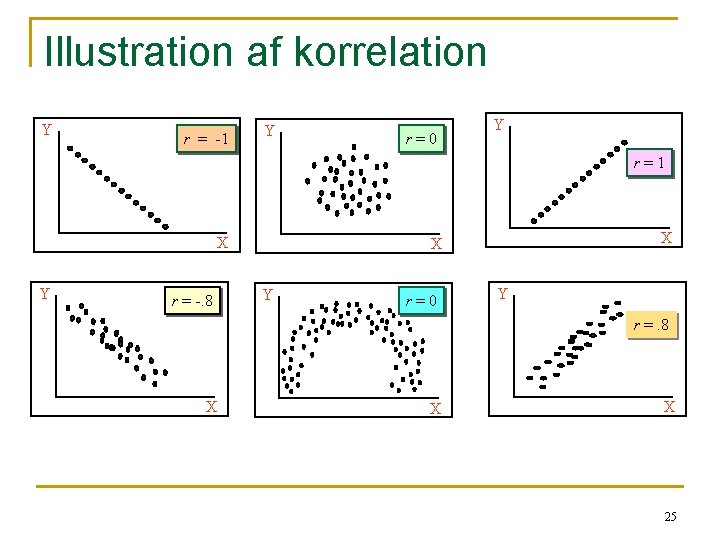
Illustration af korrelation Y r = -1 Y r=0 Y r=1 X Y r = -. 8 X X Y r=0 Y r =. 8 X X X 25

Korrelation i SPSS n Som en del af output’et for lineær regression får man bl. a. følgende kasse: Korrelationen r n Korrelationen er her r = 0. 565, dvs. en middel lineær sammenhæng. 26

Kvadratsummer n Sums of squares: q Total sum of squares: q TSS er den totale variation i yi’erne. q Sum of squared errors: SSE er den uforklarede del af variationen i yi’erne. q SSE ≤ TSS q TSS – SSE ≥ 0 den forklarede variation. q 27

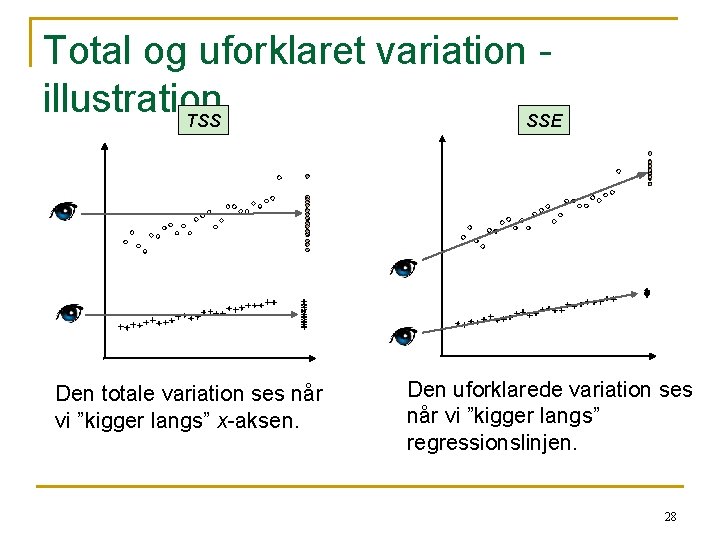
Total og uforklaret variation illustration TSS SSE Den totale variation ses når vi ”kigger langs” x-aksen. Den uforklarede variation ses når vi ”kigger langs” regressionslinjen. 28

Determinationskoefficienten r 2 n TSS – SSE n Determinationskoefficienten n Fortolkning q r 2 er andelen af den totale variation i yi’erne der er forklaret af xi’erne. q Fx: Hvis r 2 = 0. 62, så er 62% af variation i y forklaret af x. n Den totale variation Den forklarede variation 29

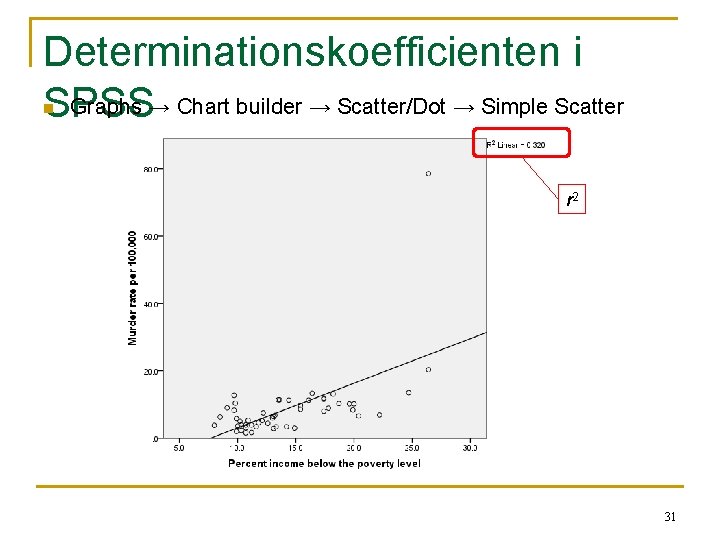
Determinationskoefficienten i SPSS n Som en del af output’et for lineær regression får man bl. a. følgende kasse: Determinationskoefficienten r 2 n Determinationskoefficienten er her r 2 = 0. 320, dvs. 32% af variationen i mordraten er forklaret af fattigdomsprocenten. 30

Determinationskoefficienten i Graphs → Chart builder → Scatter/Dot → Simple Scatter SPSS n r 2 31