Antidifferentiation by Substitution If y fx we can

Antidifferentiation by Substitution • If y = f(x) we can denote the derivative of f by either dy/dx or f’(x). What can we use to denote the antiderivative of f? – We have seen that the general solution to the differential equation dy/dx = f(x) actually consists of an infinite family of functions of the form F(x) + C, where F’(x) = f(x). • Both the name for this family of functions and the symbol we use to denote it are closely related to the definite integral because of the Fundamental Theorem of Calculus.

• The symbol is an integral sign, the function f is the integrand of the integral, and x is the variable of integration.

Evaluating an Indefinite Integral • Evaluate


Paying Attention to the Differential • Let f(x) = x³ + 1 and let u = x². Find each of the following antiderivatives in terms of x: a. ) b. ) c. )

Paying Attention to the Differential • Let f(x) = x³ + 1 and let u = x². Find each of the following antiderivatives in terms of x: a. ) b. ) c. )

• Evaluate Using Substitution • Let u = cos x du/dx = -sin x du = - sin x dx

Using Substitution • Evaluate • Let u = 5 + 2 x³, du = 6 x² dx.

Using Substitution • Evaluate • We do not recall a function whose derivative is cot 7 x, but a basic trigonometric identity changes the integrand into a form that invites the substitution u = sin 7 x, du = 7 cos 7 x dx.

Setting Up a Substitution with a Trigonometric Identity • Find the indefinite integrals. In each case you can use a trigonometric identity to set up a substitution.

Setting Up a Substitution with a Trigonometric Identity • Find the indefinite integrals. In each case you can use a trigonometric identity to set up a substitution.

Setting Up a Substitution with a Trigonometric Identity • Find the indefinite integrals. In each case you can use a trigonometric identity to set up a substitution.

Evaluating a Definite Integral by Substitution • Evaluate • Let u = tan x and du = sec²x dx.
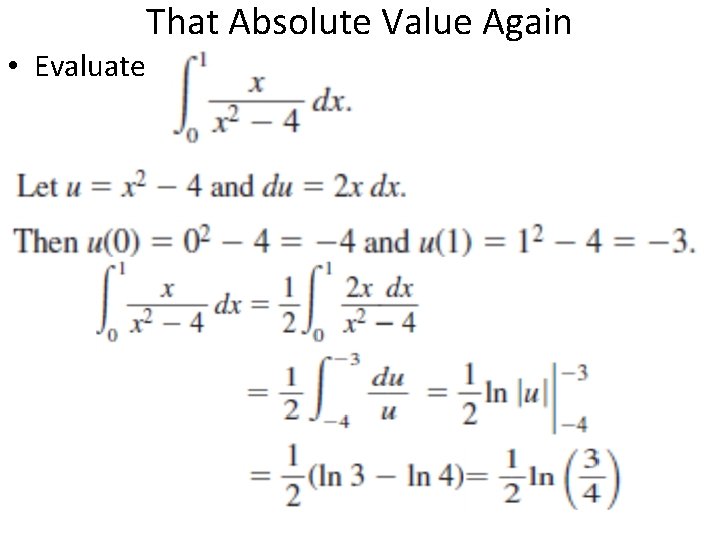
• Evaluate That Absolute Value Again
- Slides: 14