ANTENNA THEORY Chapter 3 Radiation Integrals and Auxiliary

ANTENNA THEORY Chapter 3 Radiation Integrals and Auxiliary Potential Functions JISU LEE Applied Electromagnetic Technology Laboratory Department of Electronics and Computer Engineering Hanyang University, Seoul, Korea 1/17

OUTLINE 3. 1 INTRODUCTION 3. 2 THE VECTOR POTENTIAL A FOR AN ELECRIC CURRENT SOURCE J 3. 3 THE VECTOR POTENTIAL F FOR A MAGNETIC CURRENT SOURCE M 3. 4 ELECTRIC AND MAGNETIC FIELDS FOR ELECTRIC (J) AND MAGNETIC (M) CURRENT SOURCES 3. 5 SOLUTION OF THE INHOMOGENEOUS VECTOR POTENTIAL WAVE EQUATION 3. 6 FAR-FIELD RADIATION 2/17

3. 1 INTRODUCTION § In the analysis of radiation problems, the usual procedure is to specify the sources and then require the fields radiated by the sources. § analysis procedure : to introduce vector potentials § vector potential function : (magnetic vector potential) , (electric vector potential) and Hertz potentials , § path 1 : The one-step procedure relates the and fields to and by integral relations. path 2 : The two-step procedure relates the and (or and ) potentials to and by integral relations. The integration required to determine the potential functions restricted integrands are is simple : pathover 1 <<the path 2 bounds of the sources and. The integration in the one-step procedure also requires that its limits be determined by the bounds of the sources. § vector Hertz potential is analogous to and is analogous to. The functional relation between them is a proportionality constant which is a function of the frequency and the constitutive parameters of the medium. Only one set is required. 3/17

3. 2 THE VECTOR POTENTIAL A FOR AN ELECTRIC CURRENT SOURCE J (1) § The vector potential is useful in solving for the EM field generated by a given harmonic electric current. § The magnetic flux is always solenoidal. Therefore, it can be represented as the curl of another vector because it obeys the vector identity where is an arbitrary vector. or Substituting into Maxwell’s curl equation reduces it to From the vector identity and or scalar function : arbitrary electric potential which is a function of position Taking the curl of both sides of and using the vector identity Equating Maxwell’s equation Substituting into reduces it to 4/17

3. 2 THE VECTOR POTENTIAL A FOR AN ELECTRIC CURRENT SOURCE J (2) § Define divergence of In order to simplify let which is known as the Lorentz condition. Substituting into leads to In addition, § Once is known, reduces to can be found from and from . can just as easily be found from Maxwell’s equation with . It will be shown later how to find in terms of the current density It will be a solution to the inhomogeneous Helmholtz equation of . . 5/17

3. 3 THE VECTOR POTENTIAL F FOR A MAGNETIC CURRENT SOURCE M (1) § Although magnetic currents appear to be physically unrealizable, equivalent magnetic currents arise when we use the volume or the surface equivalence theorems. § The fields generated by a harmonic magnetic current in a homogeneous region, with but , must satisfy. § Therefore, can be expressed as the curl of the vector potential by Substituting into Maxwell’s curl equation reduces it to From the vector identity of , it follows that where represents an arbitrary magnetic scalar potential which is a function of position. Taking the curl of and equating it to Maxwell’s equation 6/17

3. 3 THE VECTOR POTENTIAL F FOR A MAGNETIC CURRENT SOURCE M (2) leads to Substituting into reduces it to By letting reduces and § Once or to to is known, can be found from and with. It will be shown later how to find once is known. It will be a solution to the inhomogeneous Helmholtz equation of from . 7/17

3. 4 ELECTRIC AND MAGNETIC FIELDS FOR ELECTRIC (J) AND MAGNETIC (M) CURRENT SOURCES (1) § the procedure that can be used to find the fields is as follows 1. Specify and (electric and magnetic current density sources). 2. a. Find (due to ) using which is a solution of the inhomogeneous vector wave equation of b. Find (due to ) using which is a solution of the inhomogeneous vector wave equation of. R : the distance from any point in the source to the observation point 3. a. Find using and using. can also be found using Maxwell’s equation of with . b. Find using and using can also be found using Maxwell’s equation of 8/17

3. 4 ELECTRIC AND MAGNETIC FIELDS FOR ELECTRIC (J) AND MAGNETIC (M) CURRENT SOURCES (2) 4. The total fields are then determined by or and or § In computing fields in the far-zone, it will be easier to use for and for because, as it will be shown, the second term in each expression becomes negligible in that region. 9/17

3. 5 SOLUTION OF THE INHOMOGENEOUS VECTOR POTENTIAL WAVE EQUATION (1) § To derive the solution of the inhomogeneous vector wave equation, let us assume that a source with current density , which in the limit is an infinitesimal source, is placed at the origin of a x, y, z coordinate system. § Since the current density is directed along the zaxis ( ), only an component will exist. § At points removed from the source ( ), the wave equation reduces to § In a spherical coordinate system which when expanded reduces to § two independent solutions 10/17

3. 5 SOLUTION OF THE INHOMOGENEOUS VECTOR POTENTIAL WAVE EQUATION (2) § : an outwardly traveling wave : an inwardly traveling wave For this problem, the source is placed at the origin with the radiated fields traveling in the outward radial direction. § In the static case § In the presence of the source reduces to and k = 0, the wave equation of This equation is recognized to be Poisson’s equation. The most familiar equation with Poisson’s form is that relating the scalar electric potential �� to the electric charge density ��. whose solution is 11/17

3. 5 SOLUTION OF THE INHOMOGENEOUS VECTOR POTENTIAL WAVE EQUATION (3) § Solution of : the time-varying solution can be obtained by multiplying the static solution by § If the current densities were in the x- and y-directions ( equation for each would reduce to and . ), the wave solution : § solution to the vector wave equation of : 12/17

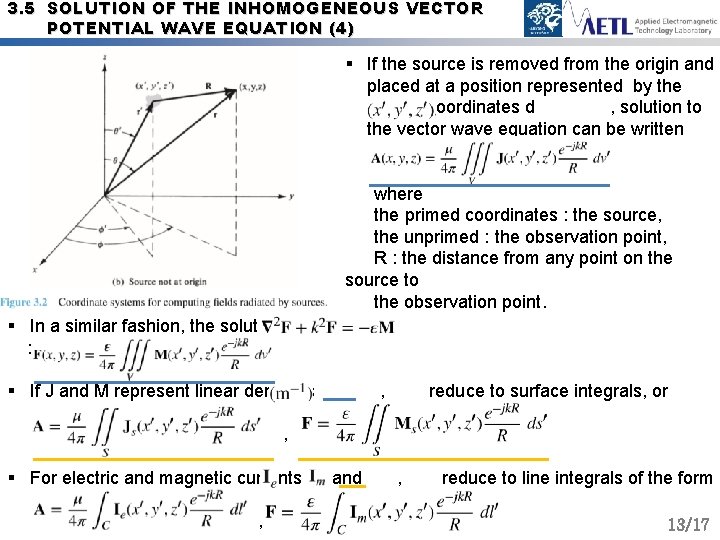
3. 5 SOLUTION OF THE INHOMOGENEOUS VECTOR POTENTIAL WAVE EQUATION (4) § If the source is removed from the origin and placed at a position represented by the primed coordinates d , solution to the vector wave equation can be written where the primed coordinates : the source, the unprimed : the observation point, R : the distance from any point on the source to the observation point. § In a similar fashion, the solution of : § If J and M represent linear densities , reduce to surface integrals, or , § For electric and magnetic currents , and , reduce to line integrals of the form 13/17

3. 6 FAR-FIELD RADIATION (1) § The fields radiated by antennas of finite dimensions are spherical waves. § For these radiators, a general solution to the vector wave equation of in spherical components, each as a function of r, �� , takes the general form of § The amplitude variations of r in each component of are of the form. Neglecting higher order terms of reduces : § Substituting into reduces it to The radial E-field component has no 1/r terms, 14/17

3. 6 FAR-FIELD RADIATION (2) § where is the intrinsic impedance of the medium. § Neglecting higher order terms of , the radiated E- and H-fields have only �� and �� components. § In a similar manner, the far-zone fields due to a magnetic source can be written as (potential ) 15/17

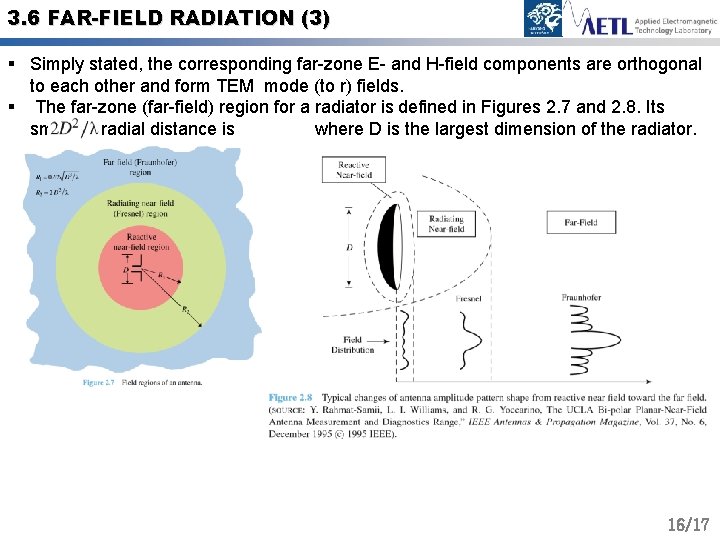
3. 6 FAR-FIELD RADIATION (3) § Simply stated, the corresponding far-zone E- and H-field components are orthogonal to each other and form TEM mode (to r) fields. § The far-zone (far-field) region for a radiator is defined in Figures 2. 7 and 2. 8. Its smallest radial distance is where D is the largest dimension of the radiator. 16/17

THANK YOU 17/17