ANSYS Basic Concepts for ANSYS Structural Analysis Contents

ANSYS Basic Concepts for ANSYS Structural Analysis

Contents 1 Disciplines and Element Types 2 Analysis Types 3 Linear Analysis and Nonlinear Analysis 4. Material Models 5. Failure Criteria of Materials 2/48

Disciplines and Element Types • • • Structural Analysis Thermal Analysis Fluid Dynamic Analysis Electric Field Analysis Magnetic Field Analysis Coupled-field Analysis 3/48

Examples • Example 1: Thermal Stress Analysis • Example 2: Structure-Fluid Interactions • Example 3: Thermal Actuator 4/48

Element Types • ANSYS elements are classified according to – Discipline – Dimensionality – Geometry – Order • Example – SOLID 45: 3 D hexahedral linear structural element – PLANE 67: 2 D quadralateral linear coupled thermal-electric element 5/48

Analysis Types • Static Analysis • Dynamic Analysis – Transient Analysis – Modal Analysis – Harmonic Response Analysis – etc. • Buckling Analysis • Structural Analysis – Static, Transient, Modal, Harmonic, Buckling, etc. • Thermal Analysis – Steady-state, Transient • Electric Field Analysis – Static, Transient, Modal, Harmonic • etc. 6/48

Transient Analysis • • Inertia forces Damping forces Elastic forces External forces 7/48

Static Analysis • When dynamic effects can be neglected, a problem can be solved statically. • Dynamic effects can be neglected only when the deformation velocity and acceleration are small. • Two cases: – Steady-state solution – approximation solution for a real-world problem. 8/48

Modal Analysis • Modal analysis is to analysis a structure under free vibration. • The solutions typically include – Vibration frequencies (or periods) – Vibration modes 9/48

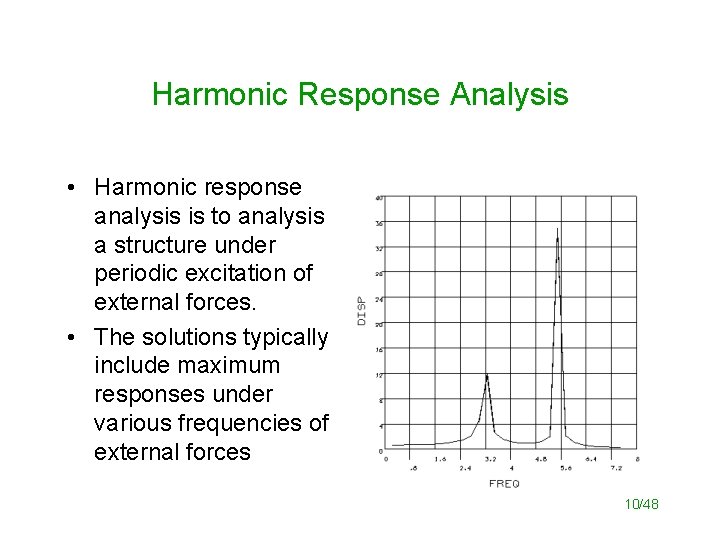
Harmonic Response Analysis • Harmonic response analysis is to analysis a structure under periodic excitation of external forces. • The solutions typically include maximum responses under various frequencies of external forces 10/48

Linear Analysis and Nonlinear Analysis 11/48

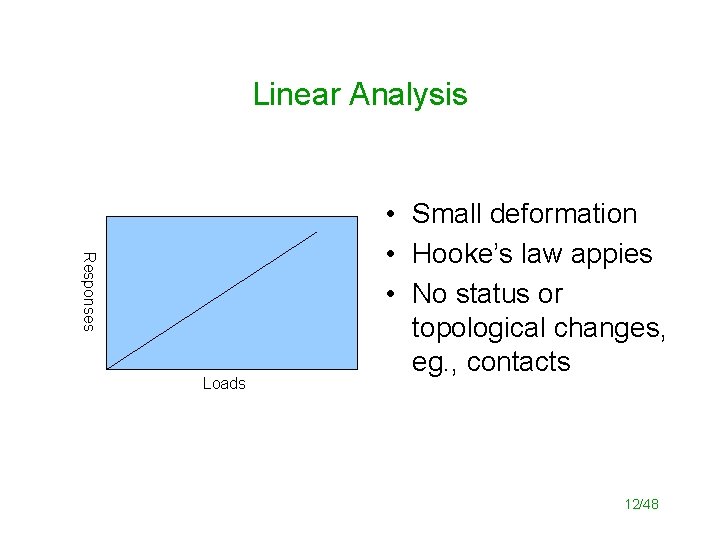
Linear Analysis Responses Loads • Small deformation • Hooke’s law appies • No status or topological changes, eg. , contacts 12/48

Nonlinear Analysis • Geometric nonlinearity • Material nonlinearity • Status nonlineaity 13/48

Material Models • Material models are mathematically represented by a set of equations called constitutive equations. • The constitutive equations describe the relations between stresses and strains (or strain rates). • The parameters in the constitutive equations are called material parameters. • ANSYS provides many material models to be chosen from. 14/48

Elastic vs. Plastic (a) Stress Strain (b) Elastic materials Stress (a) Nonlinear elastic (b) Hysteresis elastic (c) Linear Elastic Strain (c) Stress Strain 15/48

Elastic vs. Plastic materials Stress Strain 16/48

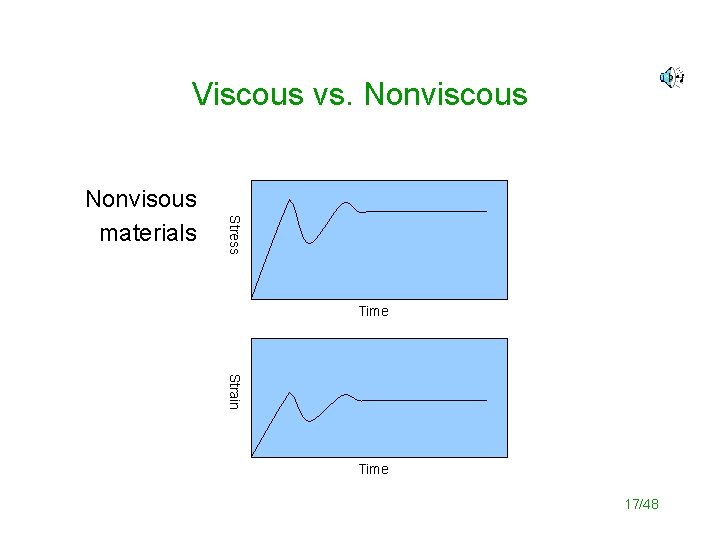
Viscous vs. Nonviscous Stress Nonvisous materials Time Strain Time 17/48

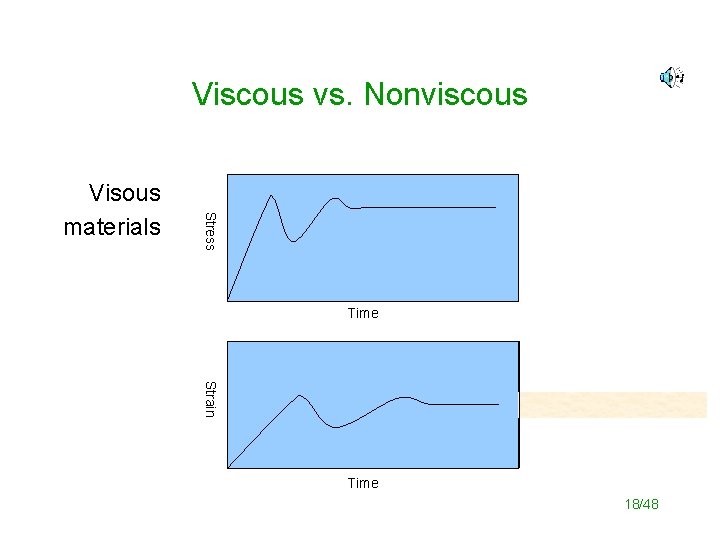
Viscous vs. Nonviscous Stress Visous materials Time Strain Time 18/48

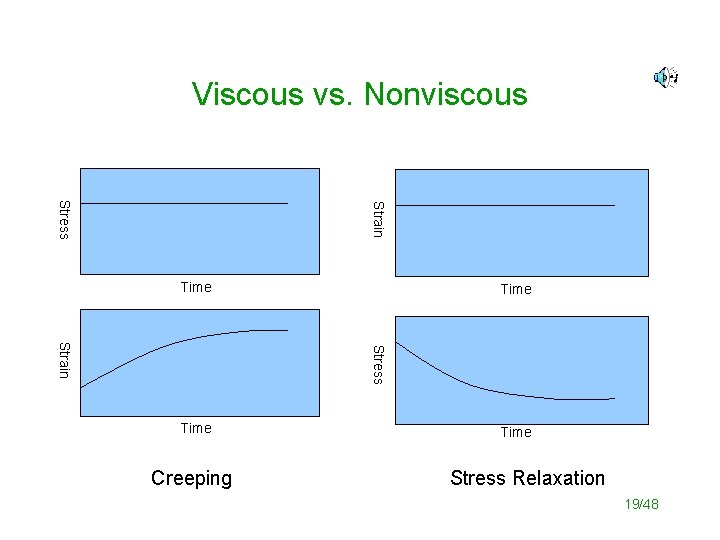
Viscous vs. Nonviscous Strain Stress Time Stress Strain Time Creeping Time Stress Relaxation 19/48

Homogeneous vs. Heterogeneous • A material body is said to be homogeneous if it has uniform material properties everywhere in the body. • Otherwise it is said to be heterogeneous. • Note that, homogeneousness does not necessarily imply isotropy. 20/48

Isotropic, Anisotropic, and Othothropic Materials • A material is said to be isotropic if it has the same material properties along any directions in the body. • Otherwise it is said to be anisotropic. • An anisotropic material is said to be orthotropic, if the planes of material symmetry are mutually orthogonal. 21/48

Isotropic, Anisotropic, and Othothropic Materials Hooke’s Law for Isotropic Material Hooke’s Law for Anisotropic Material Hooke’s Law for Orthotropic Material 22/48

Failure Criteria of Materis 23/48

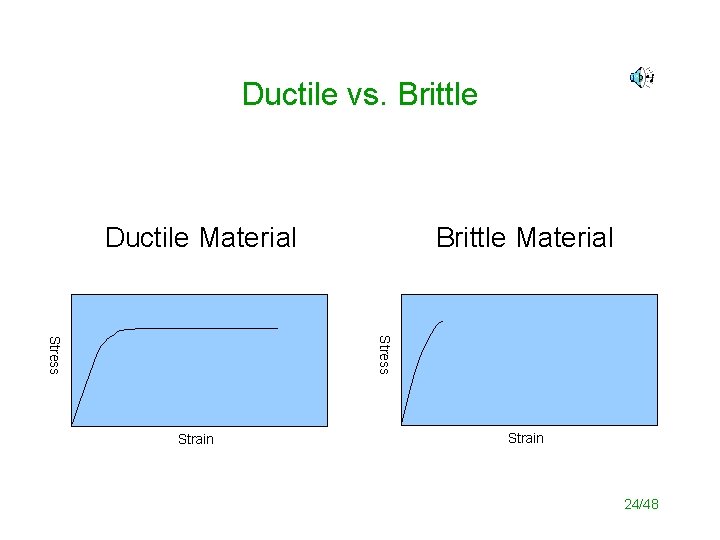
Ductile vs. Brittle Ductile Material Brittle Material Stress Strain 24/48

Failure Criteria for Brittle Materials Maximum Principal Stress Failure Criteria: • Fracture will occur when tensile stress is greater than ultimate tensile strength, i. e. , 25/48

Failure Criteria for Ductile Materials Tresca Failure Criteria: • Yielding will occur when shear stress is greater than shear yield strength, i. e. , or 26/48

Failure Criteria for Ductile Materials von Mises Failure Criteria: • Yielding will occur when the von Mises stress is greater than yield strength, i. e. , 27/48