ANOVA I Part 2 Class 14 How Do

ANOVA I (Part 2) Class 14

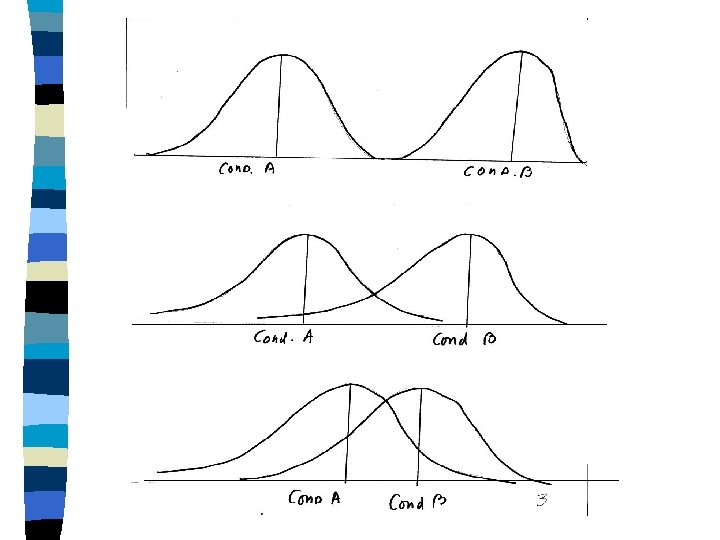
How Do You Regard Those Who Disclose? EVALUATIVE DIMENSION Good Bad Beautiful; Ugly Sweet Sour POTENCY DIMENSION Strong Weak Large Small Heavy Light ACTIVITY DIMENSION Active Passive Fast Slow Hot Cold

Birth Order Means

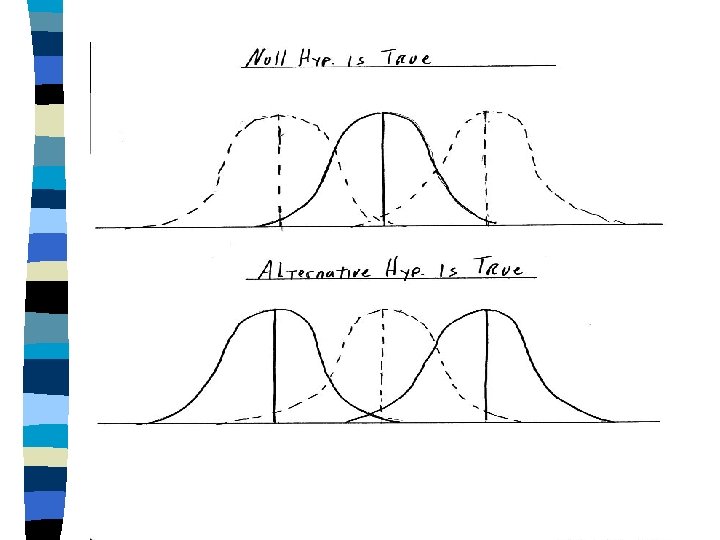
Logic of F Test and Hypothesis Testing Form of F Test: Between Group Differences Within Group Differences Purpose: Test null hypothesis: Between Group = Within Group = Random Error Interpretation: If null hypothesis is not supported (F > 1) then Between Group diffs are not simply random error, but instead reflect effect of the independent variable.

F Ratio F = Between Group Difference Within Group Differences F = Error + Treatment Effects Error

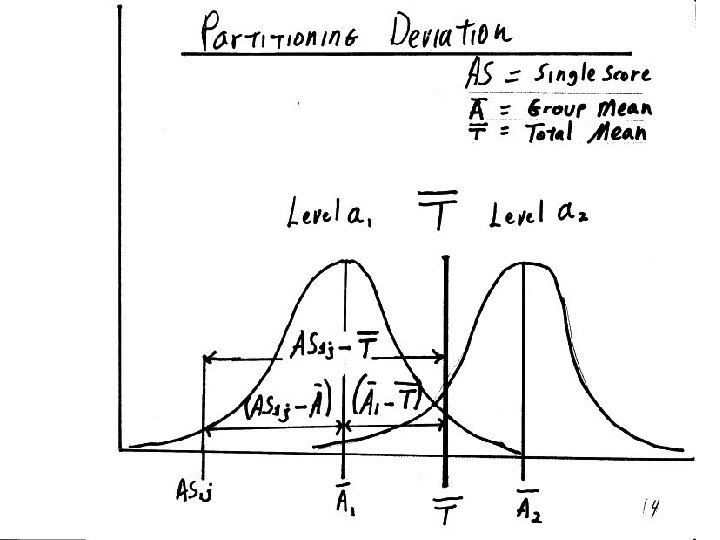
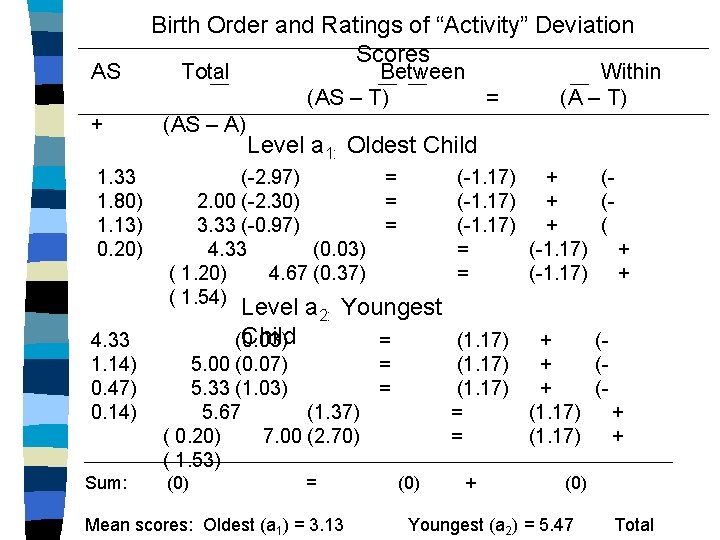
AS + Birth Order and Ratings of “Activity” Deviation Scores Total (AS – A) Between Within (AS – T) = (A – T) Level a 1: Oldest Child 1. 33 (-2. 97) = 1. 80) 2. 00 (-2. 30) = 1. 13) 3. 33 (-0. 97) = 0. 20) 4. 33 (0. 03) ( 1. 20) 4. 67 (0. 37) ( 1. 54) (-1. 17) = = + + + (-1. 17) ((( + + 4. 33 1. 14) 5. 00 (0. 07) = 0. 47) 5. 33 (1. 03) = 0. 14) 5. 67 (1. 37) ( 0. 20) 7. 00 (2. 70) ( 1. 53) ( (1. 17) + ( (1. 17) + (= (1. 17) + Level a 2: Youngest Child (0. 03) = (1. 17) + Sum: (0) = Mean scores: Oldest (a 1) = 3. 13 (0) + (0) Youngest (a 2) = 5. 47 Total

Sum of Squared Deviations Total Sum of Squares = Sum of Squared between-group deviations + Sum of Squared within-group deviations SSTotal = SSBetween + SSWithin

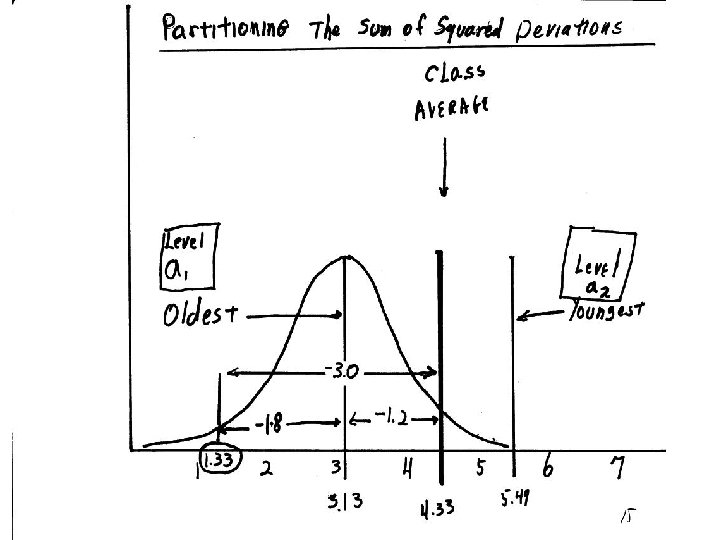
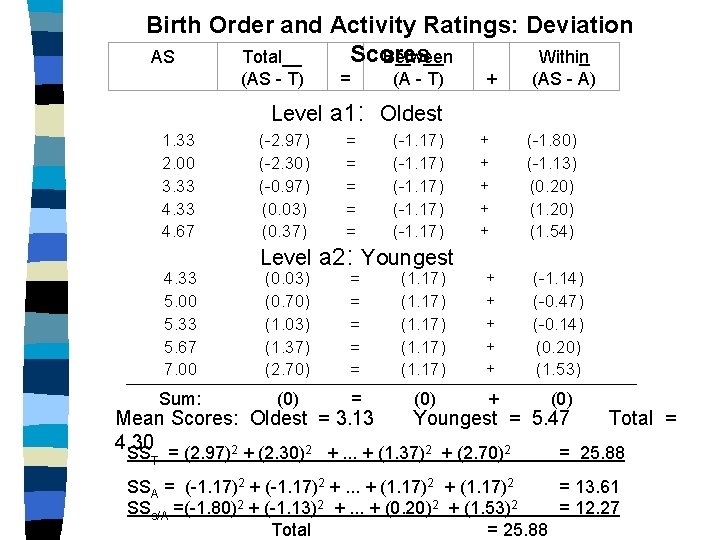
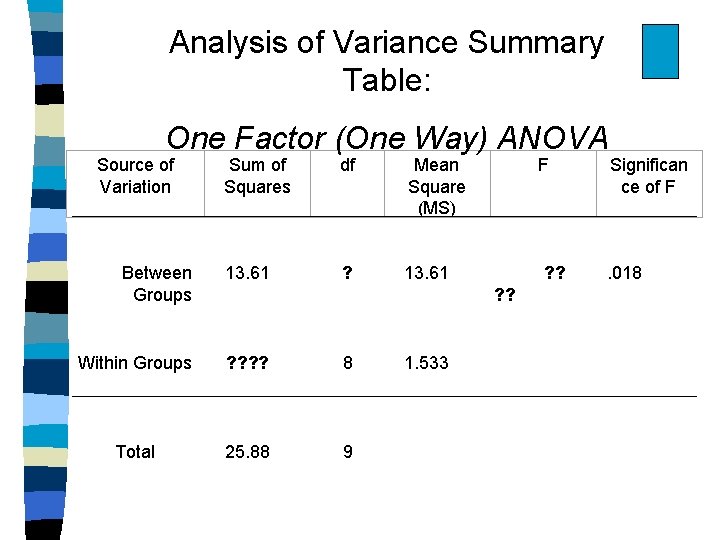
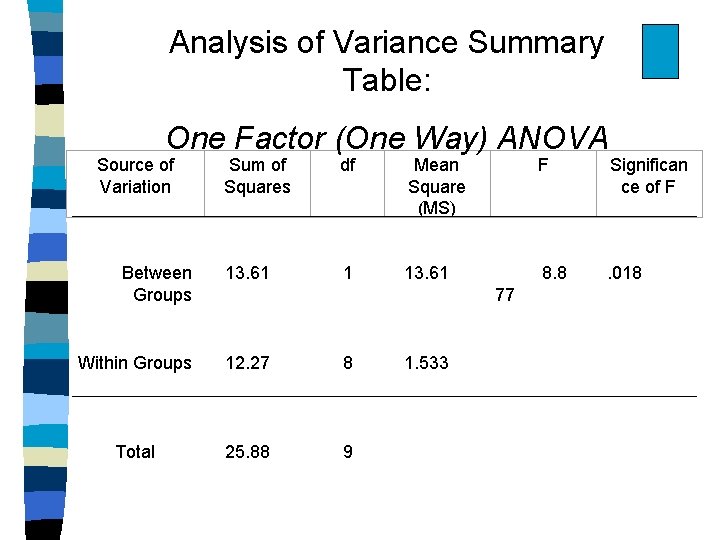
Computing Sums of Squares from Deviation Scores Birth Order and Activity Ratings (continued) = Sum of squared diffs, AKA “sum of SS squares” SST = Sum of squares. , total (all subjects) SSA = (treatment) Sum of squares, between groups SS = SSs/AT = Sum of squares, within groups (error) (2. 97)2 + (2. 30)2 + … + (1. 37)2 + (2. 70)2 = 25. 88 SSA = (1. 17)2 (-1. 17)2 + … + (1. 17)2 + = 13. 61 Total (SSA + SS s/A) = 25. 88 2 2 2 SSs/A = (-1. 80) + (-1. 13) + … + (0. 20) + (1. 53)2 = 12. 27

Birth Order and Activity Ratings: Deviation AS Total__ Scores Between Within (AS - T) = (A - T) + (AS - A) Level a 1: Oldest 1. 33 2. 00 3. 33 4. 67 (-2. 97) (-2. 30) (-0. 97) (0. 03) (0. 37) = = = (-1. 17) 4. 33 5. 00 5. 33 5. 67 7. 00 (0. 03) (0. 70) (1. 03) (1. 37) (2. 70) = = = (1. 17) + + + (-1. 14) (-0. 47) (-0. 14) (0. 20) (1. 53) (0) = (0) + (0) Sum: Level a 2: Youngest + + + (-1. 80) (-1. 13) (0. 20) (1. 54) Mean Scores: Oldest = 3. 13 Youngest = 5. 47 Total = 4. 30 2 2 SST = (2. 97) + (2. 30) +. . . + (1. 37) + (2. 70) = 25. 88 SSA = (-1. 17)2 +. . . + (1. 17)2 = 13. 61 SSs/A =(-1. 80)2 + (-1. 13)2 +. . . + (0. 20)2 + (1. 53)2 = 12. 27 Total = 25. 88

Degrees of Freedom df = Number of observations free to ? ? ? df = Number of independent Observations Number of independent Observations - Number of restraints - Number of population estimates 5 + 6 + 4 + 5 + 4 = 24 Number of observations = n = 5 Number of estimates = 1 (i. e. sum, which = 24) df = n - # estimates = 5 -X = Z 5 + 6 + 4 + 5 + 4 = 24

Degrees of Freedom df = Number of observations free to vary. df = Number of independent Observations Number of independent Observations - Number of restraints - Number of population estimates 5 + 6 + 4 + 5 + 4 = 24 Number of observations = n = 5 Number of estimates = 1 (i. e. sum, which = 24) df = n - # estimates = 5 -1 = 4 5 + 6 + 4 + 5 + 4 = 24 5 + 6 + X + 5 + 4 = 24 = 20 + X = 24 = X = 4

Degrees of Freedom for Fun and Fortune Coin flip = __ df? Dice = __ df? Japanese game that rivals cross-word puzzle?

Sudoku – The Exciting Degrees of Freedom Game 4 8 5 2 5 8 4 7 1 9 3 4 5 6 8 2 7 9 1 5 3 1 9 7 6 3 2 8 2 6

Degrees of Freedom Formulas for the Single Factor (One Way) ANOVA Source Type Formula Meaning . Groups df. A a – X Scores scores groups df dfs/A X(s – 1) Total dfs/A) df. T XY – 1 df for Tx groups; Between-groups df df for individual Within. Total df (note: df. T = df. A + Note: a = # levels in factor A; s = # subjects per condition

Degrees of Freedom Formulas for the Single Factor (One Way) ANOVA Source Type Formula Meaning . Groups df. A a – 1 dfs/A a(s – 1) df for Tx groups; Between-groups df Scores scores groups df Source Type Formula Semantic Differential Study Total df. T as – 1 dfs/A) Groups df. A a – 1 Scores dfs/A a(s – 1) Total df for individual Within. Total df (note: df. T = df. A + 2 – 1 = 1 2 (5 – 1 ) = 8 df. T (2 * 5) - 1 = 9 as – 1 (note: df. T = df. A + df Note: a = # levels in factor A; s = # subjects per condition s/A)

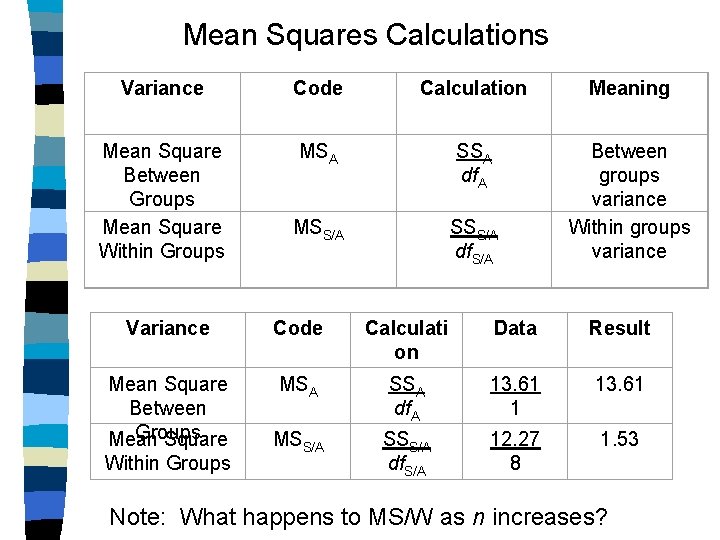
Mean Squares Calculations Variance Code Calculation Meaning Mean Square Between Groups Mean Square Within Groups MSA SSA df. A MSS/A SSS/A df. S/A Between groups variance Within groups variance Variance Code Calculati on Data Result Mean Square Between Groups Mean Square MSA SSA df. A 13. 61 1 13. 61 MSS/A SSS/A df. S/A 12. 27 8 1. 53 Within Groups Note: What happens to MS/W as n increases?

F Ratio Computation F = MSA = XXX Variance MSS/A YYYY Variance F = 13. 61 1. 51 = 8. 78

F Ratio Computation F = Variance MSA = Between Group Variance MSS/A Within Group F = 13. 61 1. 51 = 8. 78

Analysis of Variance Summary Table: One Factor (One Way) ANOVA Source of Variation Sum of Squares (SS) A SSA df Mean Square (MS) a - 1 F Ratio SSA df. A S/A SSS/A a (s- 1) Total SST as - 1 MSA MSS/A SSS/A df. S/A

Analysis of Variance Summary Table: One Factor (One Way) ANOVA Source of Variation Between Groups Sum of Squares df 13. 61 Within Groups ? ? Total 25. 88 Mean Square (MS) ? 8 9 13. 61 F Significan ce of F ? ? . 018 1. 533

Analysis of Variance Summary Table: One Factor (One Way) ANOVA Source of Variation Between Groups Sum of Squares df 13. 61 Within Groups 12. 27 Total 25. 88 Mean Square (MS) 1 8 9 13. 61 F Significan ce of F 8. 8 77 . 018 1. 533

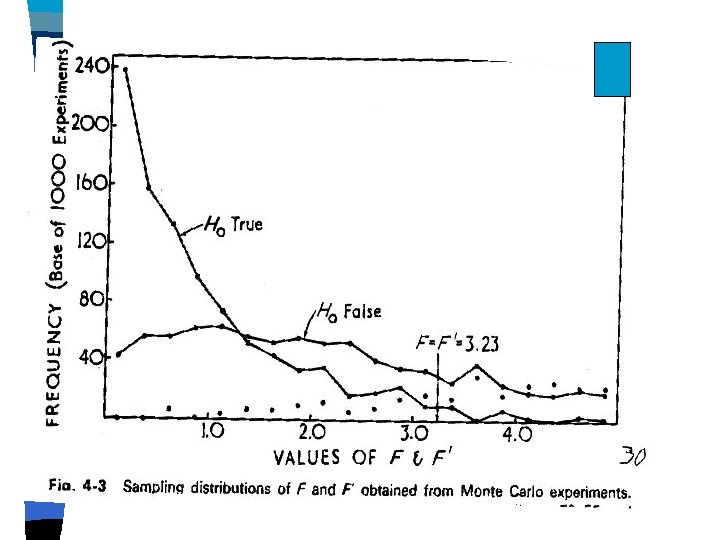
F Distribution Notation "F (1, 8)" means: The F distribution with: one df in the numerator (1 df associated with treatment groups (= between-group variation)) and 8 degrees of freedom in the denominator (8 df associated with the overall sample (= withingroup variation))

F Distribution for (2, 42) df

Criterion F and p Value For F (2, 42) = 3. 48

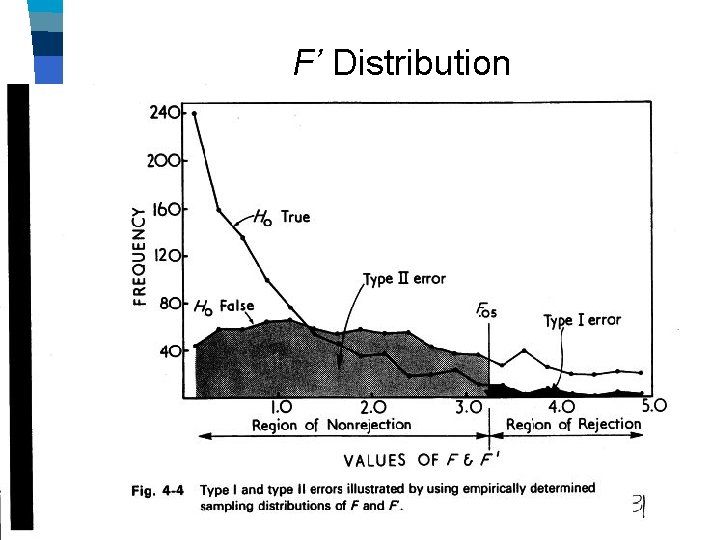
F or F′? If F is correct, then Ho supported: (First born ? ? ? Last born) If F' is correct, then H 1 supported: (First born ? ? ? Last born)

F or F′? If F is correct, then Ho supported: u 1 = u 2 (First born = Last born) If F' is correct, then H 1 supported: u 1 u 2 (First born ≠ Last born)

F’ Distribution

F Distribution Notation "F (1, 8)" means: The F distribution with: ? ? ? df in the numerator (1 df associated with treatment groups/between-group variation) and 8 degrees of freedom in the denominator (8 df associated with the ? ? ? )

F Distribution Notation "F (1, 8)" means: The F distribution with: one df in the numerator (1 df associated with treatment groups/between-group variation) and 8 degrees of freedom in the denominator (8 df associated with the overall sample/within-group variation)

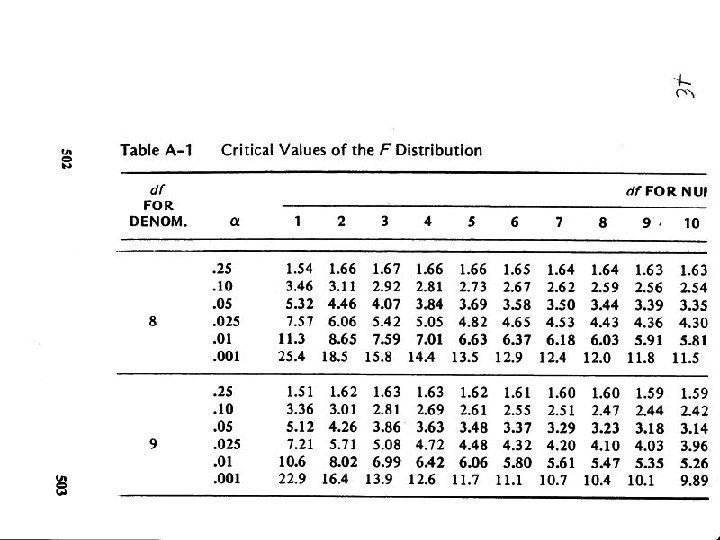
Decision Rule Regarding F Reject null hypothesis when F observed > (m, n) 8). Reject null hypothesis when F observed > 5. 32 (1, F (1, 8) = 8. 88 > = 5. 32 Decision: Reject null hypothesis Accept alternative hypothesis Note: We haven't proved alt. hypothesis, only supported it. Format for reporting our result: F (1, 8) = 8. 88, p <. 05 F (1, 8) = 8. 88, p <. 02 also OK, based on our

Summary of One Way ANOVA 1. Specify null and alt. hypotheses 2. Conduct experiment 3. Calculate F ratio Between Group Diffs 4. Within Group Diffs 4. Does F support the null hypothesis? i. e. , is Observed F > Criterion F, at p <. 05? ___ p >. 05, accept null hyp. ___ p <. 05, accept alt. hyp.