ANOVA Between and within subjects Suppose you are

ANOVA Between and within subjects Suppose you are a cell phone designer, and you would like to test four phone designs: flat, flip, folded, and telescoping. You're interested in whethere is a difference between these phone types in how much they are actually used. You enlist volunteers and give each person one phone to use for a week. Each person only gets one kind of phone. For each week, you record the number of minutes that the phones are used.

Between Subject ANOVA SSTot=SSB+SSW SSTot = Σ _ (Xij-Xg)2 Between Groups _ _ (Xj-Xg)2 MSB = ------- For all X K– 1 Within Groups _ (Xij-Xj)2 MSW = ------- For all X Ng - K SSB MSB = ------K– 1 For all X SSW MSW = ------Ng - K For all X SSW MSW = ------df. W For all X Σ SSB MSB = ------df. B Σ

Sum of Squares partitions

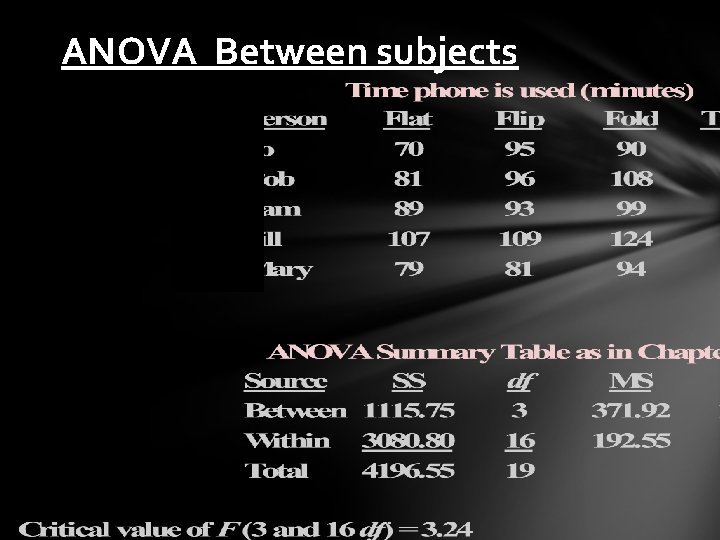
ANOVA Between subjects

ANOVA Between and within subjects After analyzing your data and failing to find a significant effect. Your boss yells at you and tells you that you better find a better way of doing the experiment or you will be fired. After discussing the situation with your roommate who ‘aced’ 100 a with that jerk Mc. Auliffe, you realize that some people are likely to use ANY phone more than other people because there is a great deal of VARIABILITY between people. If you could find a way of getting rid of the variability between people. Maybe you could find a significant effect.

ANOVA Between and within subjects After 2 Venti cups of coffee, you have a brain blast – what if you could eliminate the subject variability by having each person take part in all conditions. Similar to a dependent t-test, this would reduce variability and might help you find the effect.

ANOVA Between and within subjects You enlist volunteers and give everybody a phone with the following schedule Week 1 – flat Week 2 – flip Week 3 – folded Week 4 – telescoping For each week, you record the number of minutes that the phones are used. You collect the following data:

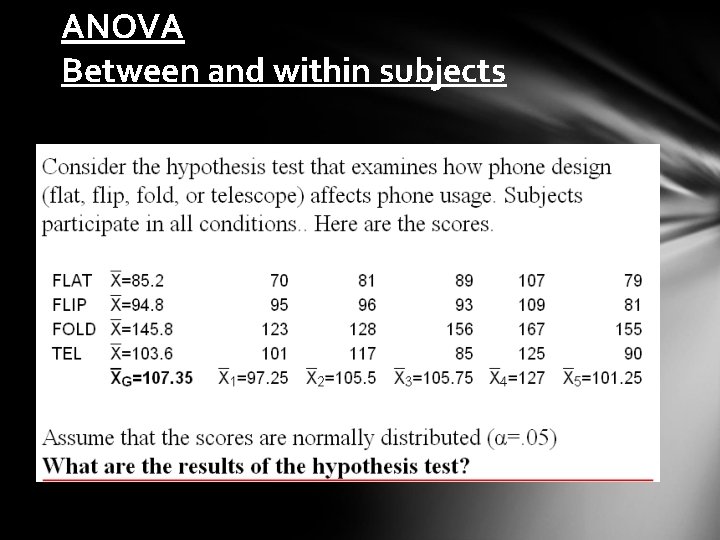
ANOVA Between and within subjects

Sum of Squares partitions

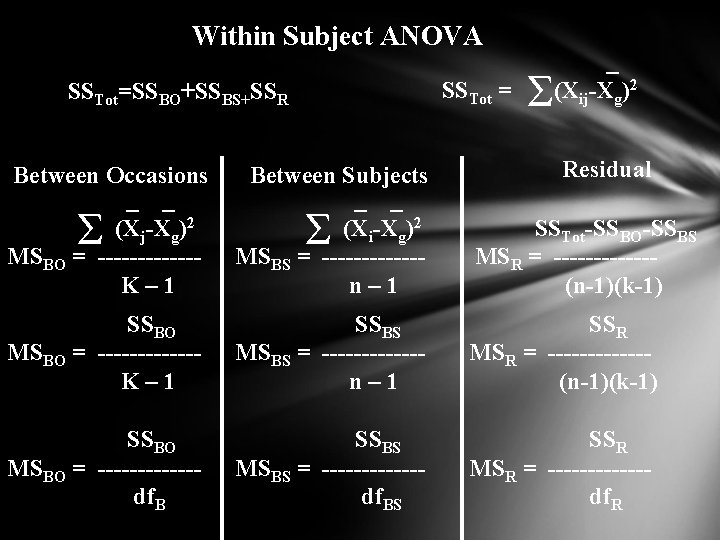
Within Subject ANOVA SSTot = SSTot=SSBO+SSBS+SSR Σ _ (Xij-Xg)2 Residual Between Occasions _ _ (Xj-Xg)2 MSBO = ------K– 1 Between Subjects _ _ (Xi-Xg)2 MSBS = ------n– 1 SSTot-SSBO-SSBS MSR = ------(n-1)(k-1) SSBO MSBO = ------K– 1 SSBS MSBS = ------n– 1 SSR MSR = ------(n-1)(k-1) SSBO MSBO = ------df. B SSBS MSBS = ------df. BS SSR MSR = ------df. R Σ Σ

Sum of Squares partitions 14526. 55 10702. 95 2125. 3 ?

Sum of Squares partitions 14526. 55 10702. 95 2125. 3 14526. 55 -10702. 95 -2125. 3= 1698. 3

ANOVA Between and within subjects Your analysis worked. You bring it to your boss expecting a pat on the back. Unfortunately, he starts yelling at you again. Why is the boss yelling at you when your results are significant?

ANOVA Between and within subjects Your boss realizes that you made a big mistake. Everyone had the folded phone during the 3 rd week of the study, but that was a vacation week when people had a lot more free time to use the phone. You’ve introduced a CONFOUNDING VARIABLE because the condition of FOLDED is CONFOUNDED with the vacation week. How do we solve this problem?

ANOVA Between and within subjects We need to make sure that there is no systematic effect of when we give people which phone. The only way to do this is to divide up the subject into 4 groups and give ¼ of the phones to each group at each time. For example. . Week 1 2 3 4 Group 1 flat flip folded tel. Group 2 flip folded tel. flat Group 3 folded tel. flat flip Group 4 tel. flat flip folded Notice how each phone design appears in all 4 weeks for different Subject groups

ANOVA Between and within subjects This is called COUNTERBALANCING and will eliminate the confound of time (also called an order effect). Because you are afraid of making a mistake, you go to your boss before you do the experiment with your new design. You are sure this will work perfectly and yet your boss still starts yelling at you. What could possibly be wrong with the design this time? Let’s look at that design again.

ANOVA Between and within subjects Group 1 Group 2 Group 3 Group 4 Anything a little weird here? Week 1 2 flat flip folded tel. flat 3 folded tel. flat flip 4 tel. flat flip folded

ANOVA Between and within subjects Group 1 Group 2 Group 3 Group 4 Week 1 2 flat flip folded tel. flat 3 folded tel. flat flip 4 tel. flat flip folded Notice that the flip phone is immediately after the flat phone in 3 out of 4 conditions. If there is some sort of carry over effect of using a flat phone, that might affect the usage of the flip phone. So maybe we could get rid of that carry over, but how? With 4 phones and 4 weeks, there’s way too many combinations to work out. So what do we do?

ANOVA Between and within subjects Time to call in the NERD RESCUE squad. Turns out, nerds have already solved this problem by working out a general solution. And it looks like this: Order Group I Group 2 Group 3 Group 4 1 A B C D 2 B D A C 3 C A D B 4 D C B A Notice how each letter follows and precedes every other letter once.

ANOVA Between and within subjects With our conditions, this looks like… Week Group I Group 2 Group 3 Group 4 1 flat flip folded tel 2 flip tel flat folded 3 folded flat tel flip 4 tel folded flip flat Notice how each condition follows and precedes every other condition once. You show it to your boss and he finally shuts up. You then collect your data and analyze it.

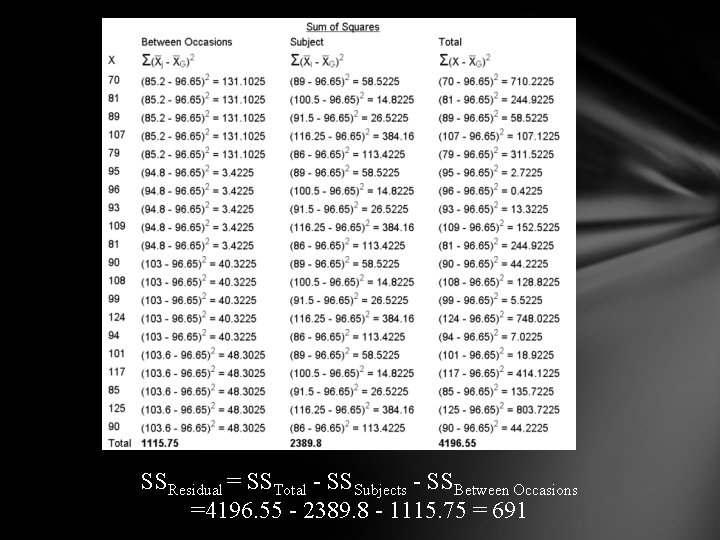
SSResidual = SSTotal - SSSubjects - SSBetween Occasions =4196. 55 - 2389. 8 - 1115. 75 = 691

Between and within subjects Critical value of F (3 and 12 df) = 3. 49 Critical value of F (3 and 16 df) = 3. 24