ANOVA Analysis of Variance Apa ANOVA Metode analisa

ANOVA (Analysis of Variance)

Apa ANOVA? � Metode analisa statistika yang termasuk ke dalam cabang statistik inferensi (penarikan kesimpulan populasi berdasarkan informasi sampel) � Merupakan teknik analisis yang digunakan untuk melakukan analisis komparasi multivariabel melalui teknik yang mengidenfikasikan dan mengukur berbagai sumber variansi dalam data � Suatu metode analisis asosiasi dengan sekumpulan prosedur yang didefinisikan dengan baik untuk menentukan perbedaan rata-rata antara tiga kelompok/sampel/populasi atau lebih

Kapan ANOVA digunakan? � Jika bertujuan untuk membandingkan rata-rata dari tiga atau lebih kelompok/kategori/sampel/populasi � Jika bertujuan untuk melakukan analisis asosiasi, dimana terdiri dari variabel bebas dengan skala pengukuran ordinal/nominal dan variabel terikat dengan skala pengukuran interval/rasio � Contoh bidang PWK: ◦ Apakah terdapat perbedaan rata-rata kepadatan penduduk di wilayah metropolitan Jabodetabek, Metropolitan Bandung Area, dan Metropolitan Surabaya Area ◦ Apakah terdapat hubungan/asosiasi harga/nilai lahan dengan lokasi lahan (pusat kota, sub pusat kota, pinggiran kota)

Beberapa asumsi yang harus dipenuhi dalam ANOVA � Data harus terdistribusi normal jika tidak normal, maka sebaiknya memperbanyak ukuran sampel � Kesamaan variansi. Setiap kelompok/kategori /sampel sebaiknya berasal dari populasi yang sama sehingga memiliki variansi yang sama pula. Jika banyaknya sampel sama di masing-masing kategori/kelompok maka asumsi kesamaan variansi ini dapat diabaikan � Pengambilan sampel seharusnya random (acak), sehingga setiap pengamatan merupakan informasi yang bebas

Prinsip ANOVA � Pengujian perbedaan rata-rata antar tiga atau lebih kelompok/kategori/sampel/populasi didasarkan pada besar “Variansi Between” kelompok/kategori/sampel/populasi dengan besar “Variansi Within” kelompok/ kategori/sampel/populasi � Variansi Between adalah metode untuk menghitung variabilitas antar kelompok/kategori dengan melihat perbedaan mean dari masing kelompok/kategori terhadap total kelompok/kategori

Prinsip ANOVA � Variansi Within adalah metode untuk menghitung variabilitas di masing-masing kelompok/kategori dengan melihat perbedaan mean terhadap setiap unit data/pengamatan � Uji dalam ANOVA menggunkan uji F karena dipakai untuk pengujian lebih dari dua sampel/populasi berbeda dengan uji t yang digunakan dalam pengujian hipotesis

Jenis-jenis ANOVA � One Way ANOVA (Klasifikasi 1 arah) � Two Way ANOVA (Klasifikasi 2 arah) ◦ ANOVA digunakan jika didasarkan pada pengamatan 1 kriteria/faktor yang menimbulkan variasi ◦ Contoh: perbedaan jumlah penduduk berdasarkan kriteria/faktor tingkat kelahiran (tingkat kelahiran tinggi, sedang, rendah) ◦ ANOVA digunakan jika didasarkan pada pengamatan 2 kriteria/faktor yang menimbulkan variasi ◦ Contoh: perbedaan jumlah penduduk berdasarkan kriteria/faktor tingkat kelahiran (tingkat kelahiran tinggi, sedang, rendah) dan tingkat kematian (tingkat kematian tinggi, sedang, rendah) � MANOVA (Klasifikasi banyak arah) ◦ ANOVA digunakan jika didasarkan pada pengamatan lebih dari 2 kriteria/faktor yang menimbulkan variasi ◦ Contoh: perbedaan jumlah penduduk berdasarkan kriteria/faktor tingkat kelahiran , tingkat kematian dan tingkat migrasi

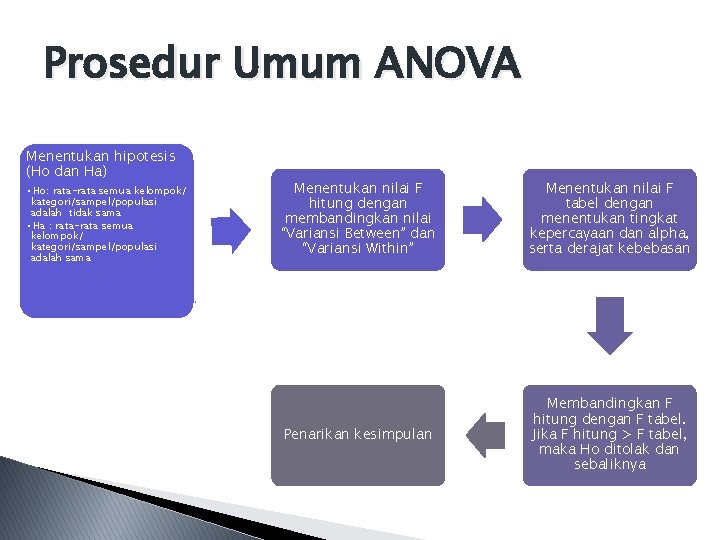
Prosedur Umum ANOVA Menentukan hipotesis (Ho dan Ha) • Ho: rata-rata semua kelompok/ kategori/sampel/populasi adalah tidak sama • Ha : rata-rata semua kelompok/ kategori/sampel/populasi adalah sama Menentukan nilai F hitung dengan membandingkan nilai “Variansi Between” dan “Variansi Within” Menentukan nilai F tabel dengan menentukan tingkat kepercayaan dan alpha, serta derajat kebebasan Penarikan kesimpulan Membandingkan F hitung dengan F tabel. Jika F hitung > F tabel, maka Ho ditolak dan sebaliknya

One Way ANOVA

Kapan digunakan? � Apabila data yang akan dianalisis terdiri dari satu variabel bebas dengan skala pengukuran ordinal/nominal dan satu variabel terikat dengan skala pengukuran interval/rasio � Contoh: ◦ perbedaan jumlah penduduk berdasarkan kriteria/faktor tingkat kelahiran (tingkat kelahiran tinggi, sedang, rendah). Pada kasus ini variabel bebas yang dimaksud adalah Tingkat Kelahiran yang diukur dengan skala ordinal, variabel terikat adalah Jumlah Penduduk yang diukur dengan skala rasio ◦ Dengan one way ANOVA akan menjawab apakah perbedaan tingkat kelahiran memiliki efek terhadap jumlah penduduk atau tidak

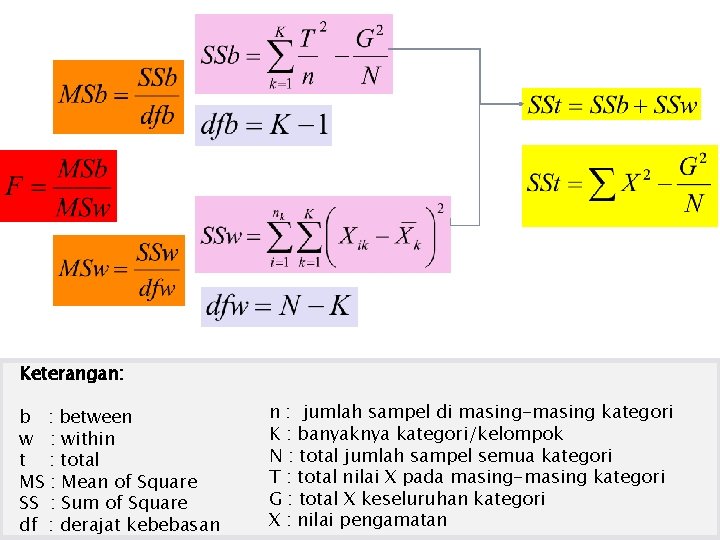
Tahapan One Way ANOVA 1. 2. Menentukan hipotesis (Ho dan Ha) Menentukan nilai F hitung, yaitu rasio antara besar variansi antar kelompok/kategori (Variance Between) dengan variansi dalam kelompok/kategori (Variance Within) q Variance Between dinotasikan MSb q Variance Within dinotasikan MSw

Keterangan: b : between w : within t : total MS : Mean of Square SS : Sum of Square df : derajat kebebasan n : jumlah sampel di masing-masing kategori K : banyaknya kategori/kelompok N : total jumlah sampel semua kategori T : total nilai X pada masing-masing kategori G : total X keseluruhan kategori X : nilai pengamatan

Tahapan One Way ANOVA 3. Menentukan nilai F tabel ü ü 4. 5. Tentukan alpha (α) melalui tingkat kepercayaan yang digunakan Tentukan derajat kebebasan (df): dfb dan dfw. Dalam tabel distribusi F, dfb sebagai pembilang/numerator dan dfw sebagai penyebut/denominator Membandingkan F hitung dengan F tabel q Jika F hitung lebih besar dari F tabel , Ho ditolak q Jika hitung sama dengan atau kurang dari F tabel, Ho diterima Penarikan kesimpulan

Contoh Kasus � Sebuah penelitian bertujuan untuk mengkaji bagaimana pengaruh/efek lokasi terhadap harga/nilai lahan. Pengambilan data dilakukan secara random pada 6 titik pengamatan di 3 lokasi (pusat kota, sub pusat kota, dan pinggiran) seperti pada tabel berikut. Apakah faktor lokasi berpengaruh terhadap harga/nilai lahan?

Penyelesaian Kasus � Menentukan hipotesis: 1 v. Ho: µA= µB= µC (rata-rata harga/nilai lahan ketiga lokasi adalah sama) v. Ha: µ 1 ≠ µ 2 ≠ µ 3 rata-rata harga/nilai lahan ketiga lokasi adalah tidak sama) Atau dalam kalimat verbal dibuat: v. Ho : faktor lokasi tidak mempengaruhi perbedaan harga/nilai lahan v. Ha : faktor lokasi mempengaruhi perbedaan harga/nilai lahan

Penyelesaian Kasus � Menentukan nilai F hitung 2

Penyelesaian Kasus � Menentukan nilai F tabel ◦ Tingkat kepercayaan 95%, maka alpha adalah 5%. Tingkat kepercayaan 99%, maka alpha adalah 1% ◦ Nilai dfb dan dfw ◦ Dengan alpha 0, 05; F (2, 6) = 5, 14 ◦ Dengan alpha 0, 01; F (2, 6) = 10, 92 3

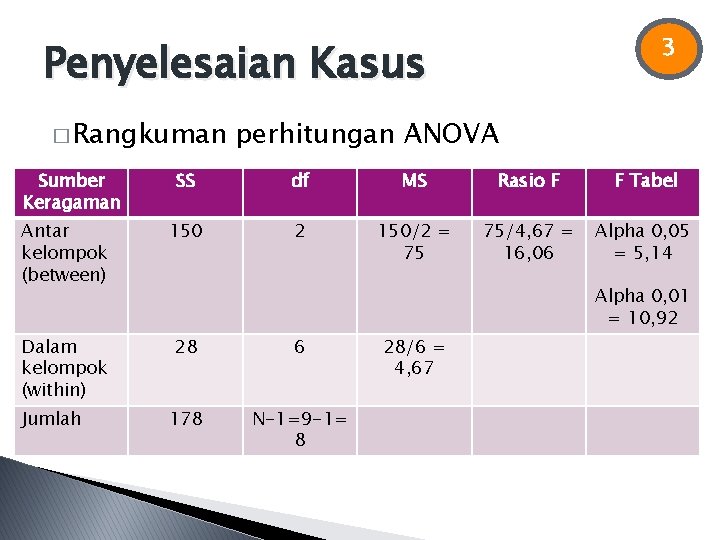
3 Penyelesaian Kasus � Rangkuman Sumber Keragaman perhitungan ANOVA SS df MS Rasio F F Tabel Antar kelompok (between) 150 2 150/2 = 75 75/4, 67 = 16, 06 Alpha 0, 05 = 5, 14 Dalam kelompok (within) 28 6 178 N-1=9 -1= 8 Jumlah Alpha 0, 01 = 10, 92 28/6 = 4, 67

Penyelesaian Kasus Membandingkan F hitung dengan F tabel 4 ◦ F hitung = 16, 06 ◦ F tabel (alpha 0, 05) = 5, 14 ◦ F tabel (alpha 0, 01) = 10, 92 Maka F hitung > F tabel Ho ditolak, artinya rata-rata harga/nilai lahan berbeda menurut lokasi Penarikan kesimpulan: Faktor lokasi mempengaruhi perbedaan harga/nilai lahan

Two Way ANOVA

Kapan digunakan? � Apabila data yang akan dianalisis terdiri dari satu variabel terikat dan dua variabel bebas � Contoh: ◦ perbedaan jumlah penduduk berdasarkan kriteria/faktor tingkat kelahiran (tinggi, sedang, rendah) dan tingkat kematian (tinggi, sedang, rendah). Pada kasus ini variabel bebas yang dimaksud adalah Tingkat Kelahiran dan Tingkat Kematian yang diukur dengan skala ordinal, variabel terikat adalah Jumlah Penduduk yang diukur dengan skala rasio ◦ Dengan two way ANOVA akan menjawab apakah perbedaan tingkat kelahiran dan tingkat kematian memiliki efek terhadap jumlah penduduk atau tidak

Ilustrasi Kasus Two Way ANOVA Tingkat Kematian (A) Tingkat Kelahiran (B) Tinggi Sedang Rendah Tinggi X 11 X 12 X 13 Sedang X 21 X 22 X 23 Rendah X 31 X 32 X 33 Faktor Tingkat Kelahiran dan Tingkat Kematian mempengaruhi perbedaan jumlah penduduk (X 11…. . X 33)

Tahapan Two Way ANOVA 1. Menentukan hipotesis (Ho dan Ha) 1. 2. 3. Yang berkaitan dengan pengaruh faktor pertama (A) atau efek baris Yang berkaitan dengan pengaruh faktor kedua (B) atau efek kolom Interaksi A x B Menentukan nilai F hitung, yaitu rasio antara besar variansi antar kelompok/kategori (Variance Between) dengan variansi dalam kelompok/kategori (Variance Within). Perhitungan rasio F terdiri dari 3 macam: q FA q FB q FAB

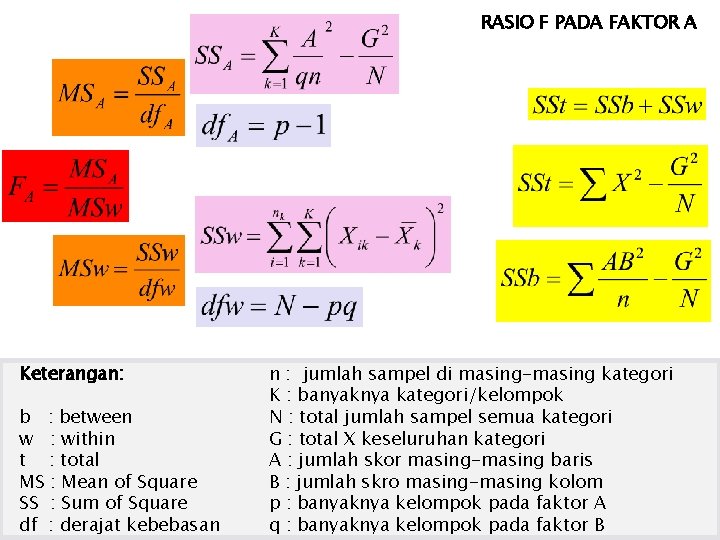
RASIO F PADA FAKTOR A Keterangan: b : between w : within t : total MS : Mean of Square SS : Sum of Square df : derajat kebebasan n : jumlah sampel di masing-masing kategori K : banyaknya kategori/kelompok N : total jumlah sampel semua kategori G : total X keseluruhan kategori A : jumlah skor masing-masing baris B : jumlah skro masing-masing kolom p : banyaknya kelompok pada faktor A q : banyaknya kelompok pada faktor B

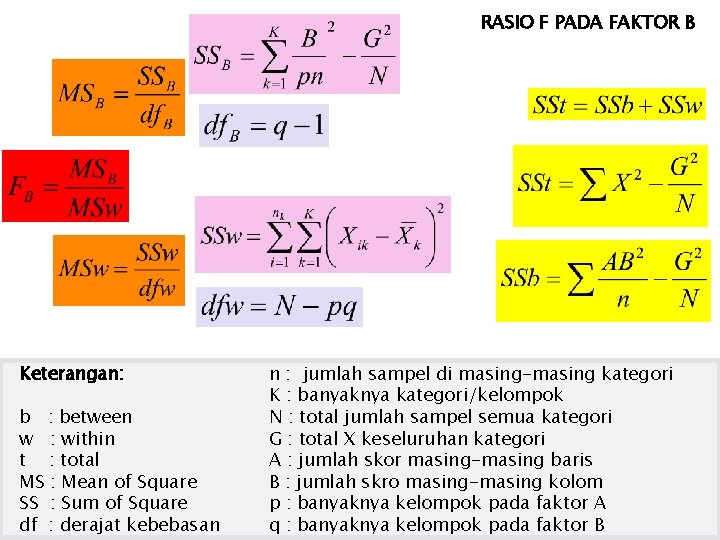
RASIO F PADA FAKTOR B Keterangan: b : between w : within t : total MS : Mean of Square SS : Sum of Square df : derajat kebebasan n : jumlah sampel di masing-masing kategori K : banyaknya kategori/kelompok N : total jumlah sampel semua kategori G : total X keseluruhan kategori A : jumlah skor masing-masing baris B : jumlah skro masing-masing kolom p : banyaknya kelompok pada faktor A q : banyaknya kelompok pada faktor B

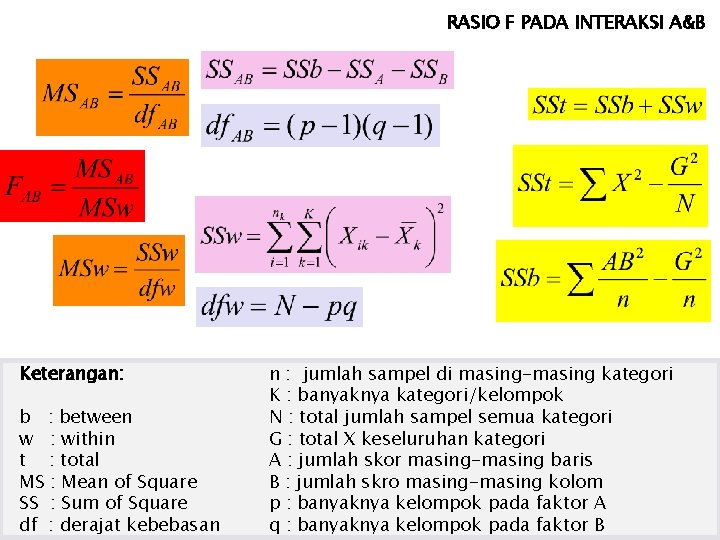
RASIO F PADA INTERAKSI A&B Keterangan: b : between w : within t : total MS : Mean of Square SS : Sum of Square df : derajat kebebasan n : jumlah sampel di masing-masing kategori K : banyaknya kategori/kelompok N : total jumlah sampel semua kategori G : total X keseluruhan kategori A : jumlah skor masing-masing baris B : jumlah skro masing-masing kolom p : banyaknya kelompok pada faktor A q : banyaknya kelompok pada faktor B

Tahapan Two Way ANOVA 3. Menentukan nilai F tabel ü ü 4. 5. Tentukan alpha (α) melalui tingkat kepercayaan yang digunakan Tentukan derajat kebebasan (df): df. A, df. B, df. AB. Dalam tabel distribusi F, df. A, df. B, df. AB sebagai pembilang/numerator dan dfw sebagai penyebut/denominator Membandingkan F hitung dengan F tabel q Jika F hitung lebih besar dari F tabel , Ho ditolak q Jika hitung sama dengan atau kurang dari F tabel, Ho diterima Penarikan kesimpulan

Contoh Kasus � Sebuah penelitian bertujuan untuk mengkaji bagaimana pengaruh/efek lokasi dan efek jarak dengan fasilitas terhadap harga/nilai lahan. Pengambilan data dilakukan secara random pada 30 titik pengamatan seperti pada tabel berikut. Apakah faktor lokasi dan faktor kedekatan dengan fafsilitas berpengaruh terhadap harga/nilai lahan?

Penyelesaian Kasus � Menentukan hipotesis: 1 ◦ Pengaruh Faktor Pertama (A) atau Efek kedekatan dengan fasilitas (efek baris) v Ho: µA 1= µA 2 (rata-rata harga/nilai lahan berdasarkan kedekatan dengan fasilitas adalah sama) v Ha: µA 1 ≠ µA 2 (rata-rata harga/nilai lahan berdasarkan kedekatan dengan fasilitas adalah tidak sama) ◦ Pengaruh Faktor Kedua (B) atau Efek lokasi (efek kolom) v Ho: µB 1= µB 2 = µB 3 (rata-rata harga/nilai lahan ketiga lokasi adalah sama) v Ha: µB 1 ≠ µB 2 ≠ µB 3 (rata-rata harga/nilai lahan ketiga lokasi adalah tidak sama) ◦ Interaksi A x B v Ho: efek faktor A tidak tergantung pada efek faktor B, dan sebaliknya v Ha: efek faktor A tergantung pada efek faktor B, dan sebaliknya

Penyelesaian Kasus � Menentukan nilai F hitung Dari tabel di atas dapat diketahui: A 1 =94 A 2 =107 B 1 =55 B 2 =67, 5 B 3 =78, 5 G =201 p =2 q =3 2

Penyelesaian Kasus � Menentukan nilai F hitung N =30 2

HITUNG RASIO F PADA FAKTOR A (BARIS)

HITUNG RASIO F PADA FAKTOR B (KOLOM)

HITUNG RASIO F PADA INTERAKSI AXB

Penyelesaian Kasus � Menentukan nilai F tabel ◦ Tingkat kepercayaan 95%, maka alpha adalah 5%. ◦ Nilai derajat kebebasan (df): df. A, df. B, df. AB dan dfw ◦ Dengan alpha 0, 05; nilai F tabel: �F tabel A (1, 24) = 4, 26 �F tabel B (2, 24) = 3, 40 �F tabel AB (2, 24) = 3, 40 3

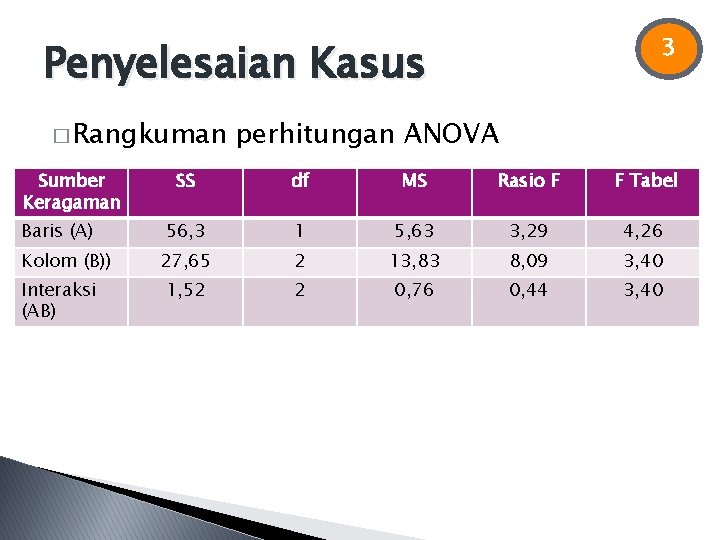
3 Penyelesaian Kasus � Rangkuman Sumber Keragaman Baris (A) Kolom (B)) Interaksi (AB) perhitungan ANOVA SS df MS Rasio F F Tabel 56, 3 1 5, 63 3, 29 4, 26 27, 65 2 13, 83 8, 09 3, 40 1, 52 2 0, 76 0, 44 3, 40

Penyelesaian Kasus 4 Membandingkan F hitung dengan F tabel ◦ Pengaruh Faktor Pertama (A) atau Efek kedekatan dengan fasilitas (efek baris) �FA < F tabel A Ho diterima ◦ Pengaruh Faktor Kedua (B) atau Efek lokasi (efek kolom) �FB > F tabel B Ho ditolak ◦ Interaksi A x B �FAB < F tabel AB Ho diterima Penarikan kesimpulan: Faktor kedekatan fasilitas tidak mempengaruhi perbedaan harga/nilai lahan, namun faktor lokasi mempengaruhi perbedaan harga/nilai lahan. Pengaruh faktor lokasi terhadap harga/nilai lahan tidak tergantung pada faktor kedekatan dengan fasilitas.

KELEMAHAN ANOVA v Jumlah masing-masing sampel pada setiap kategori perlu sama, untuk menjamin kesamaan variansi antar populasi v H 1 diterima tidak menjelaskan berapa kategori yang mempunyai rata-rata yang sama dan juga tidak diketahui kategori mana yang mempunyai perbedaan dengan yang lain.

Latihan Soal - CONTOH KASUS ANOVA To be continued…

Penjelasan � Buatlah kelompok yang beranggotakan maksimum 5 orang � Kerjakan 2 soal berikut secara berkelompok pada lembar jawaban yang diberikan � Pengerjaan soal: 50 menit � Pembahasan soal: 50 menit � Diskusi Tanya Jawab: 20 menit

SEKIAN DAN TERIMAKASIH Q&A