Anorganick chemie I pro studenty Pedagogick fakulty OPBE

Anorganická chemie (I) pro studenty Pedagogické fakulty (OPBE 022 A ) V tomto souboru naleznete podklady ke dvanácti přednáškám (2 hodiny týdně) probíhajících v letním semestru. Doplňkem přednášek je dvouhodinový seminář.

Úvodní přednáška se zabývá stavbou atomu: - historický přehled a vývoj dřívějších a současných představ o stavbě atomu - jádro versus elektronový obal - klasická mechanika versus kvantová mechanika - řešení Schrödingerovy rovnice (operátorové rovnice, sférické souřadnice) - vlnová funkce a pravděpodobnost výskytu elektronu

Soubor vlnových funkcí vypočtených řešením Schrödingerovy rovnice

Řešením Schrödingerovy rovnice získáme soubor funkcí obsahujících parametry n, l, m ležících v oboru celých čísel. Mezi těmito parametry platí následující vztahy: „n“ může nabývat hodnot 1, 2, 3, 4, 5, 6… „l “ může nabývat hodnot „ 0, 1, 2, 3, …n− 1“ „m“ může nabývat hodnot „(−l ), (−l+1), … 0, 1, …+l “ Každá vlnová funkce pro příslušnou kombinaci výše uvedených (kvantových) čísel má radiální část (závislou pouze na proměnné ρ) a angulární část (závislou na proměnných θ a Φ). Tam, kde angulární část nezávisí na proměnných θ a Φ (je konstantní) je vlnová funkce závislá pouze na proměnné ρ, tj. na vzdálenosti od jádra. Vztah vlnové funkce a pravděpodobnosti výskytu elektronu je dána výrazem P = ψ·ψ*, v oboru reálných čísel je pak tedy pravděpodobnost rovna druhé mocnině vlnové funkce. Položíme-li pravděpodobnost rovnou konstantě, získáme izoplochu pravděpodobnosti, která vytváří tvar „orbitalu“. Funkce, které nemají angulární část závislou na proměnných θ a Φ jsou kulově symetrické („orbitaly s“). Funkce s parametrem l =1 představují p-orbitaly, funkce s l =2 pak d-orbitaly atd. V další části přednášky jsou popsány orbitaly s, p, a d včetně jejich prostorové orientace a nodálních ploch. Každý orbital představuje dvě téměř identické vlnové funkce lišící se čtvrtým parametrem („spinem“), matematicky formulovaným jako další kvantové číslo nabývající hodnoty +1/2 a − 1/2.

Teorie molekulových orbitalů Použijeme-li stejný přístup k výpočtu složitějších molekul (to, co bylo doposud odvozeno platí pouze pro vodíkový atom – chování jednoho elektronu v poli jádra o jednotkovém náboji), dostaneme se k teorii molekulových orbitalů, která používá stejný kvantově-mechanický přístup k řešení složitějších molekul. Tyto molekuly však již nelze vyřešit exaktně – je třeba použít různých aproximací a zjednodušení. Jednou z nich je tzv. lineární kombinace atomových orbitalů, tzv. „MO LCAO“. Tato teorie nám poskytuje alespoň u biatomických molekul a iontů základní informaci o tom, jestli příslušná molekula (ion) může vzniknout, jaký v ní bude vazebný řád a také jednoznačnou informaci o počtu nepárových elektronů. Na základě této teorie bylo např. poprvé objasněno, proč je molekula kyslíku (O 2) paramagnetická.

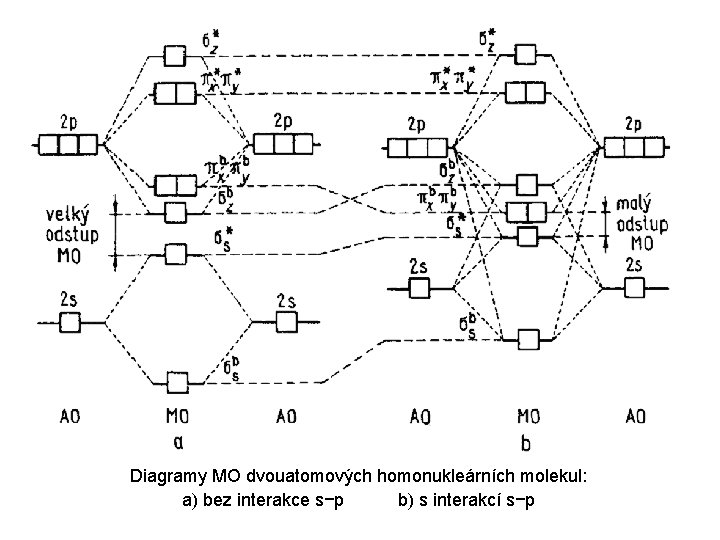
Diagramy MO dvouatomových homonukleárních molekul: a) bez interakce s−p b) s interakcí s−p

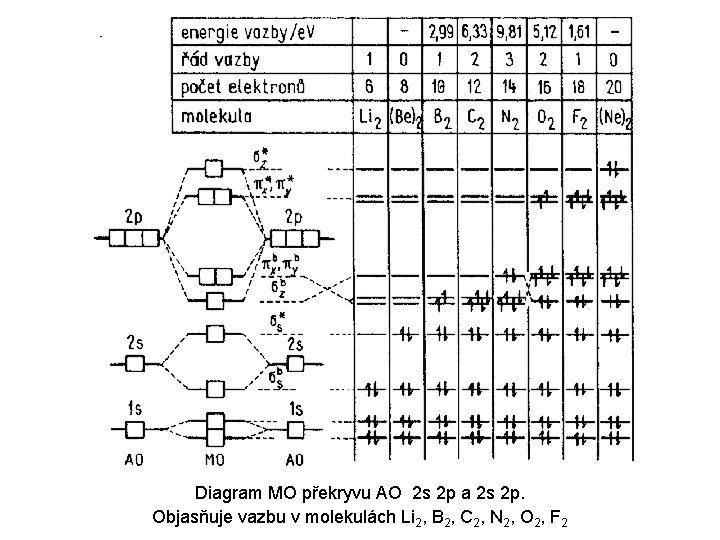
Diagram MO překryvu AO 2 s 2 p a 2 s 2 p. Objasňuje vazbu v molekulách Li 2, B 2, C 2, N 2, O 2, F 2

MODEL VSEPR ( Valence Shell Electron Pair Repulsion = Odpuzování elektronových párů valenční sféry) Teorie molekulových orbitalů nám sice u jednoduchých molekul odpoví na otázky uvedené výše (samotná existence molekuly, řád vazby a počet nepárových elektronů), předpověď tvaru víceatomových molekul však rozhodně není podle této teorie triviální záležitostí. Model „VSEPR“, jehož použitelnost je omezená na atomy nepřechodných prvků však snadno poskytne informaci o tvaru takové molekuly: 1) 2) 3) Nakreslete správně elektronový vzorec příslušné molekuly Sečtěte všechny σ-vaby a volné elektronové páry na centrálním atomu Na základě takto získaného čísla určete základní tvar molekuly (viz následující tabulka)

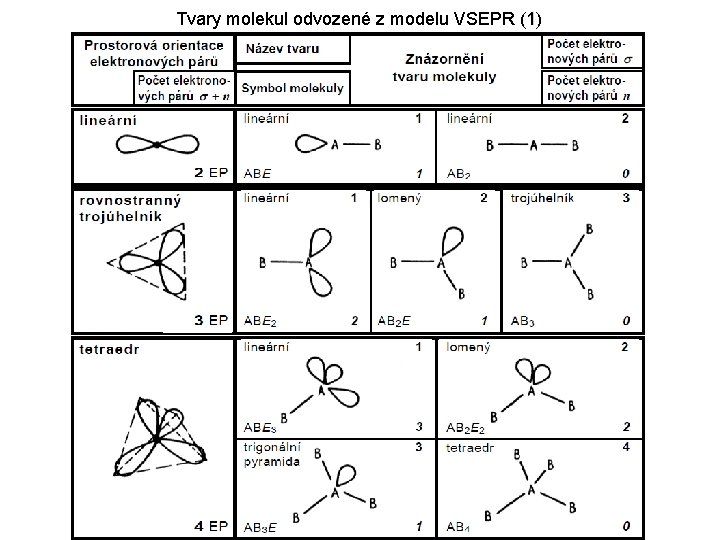
Tvary molekul odvozené z modelu VSEPR (1)

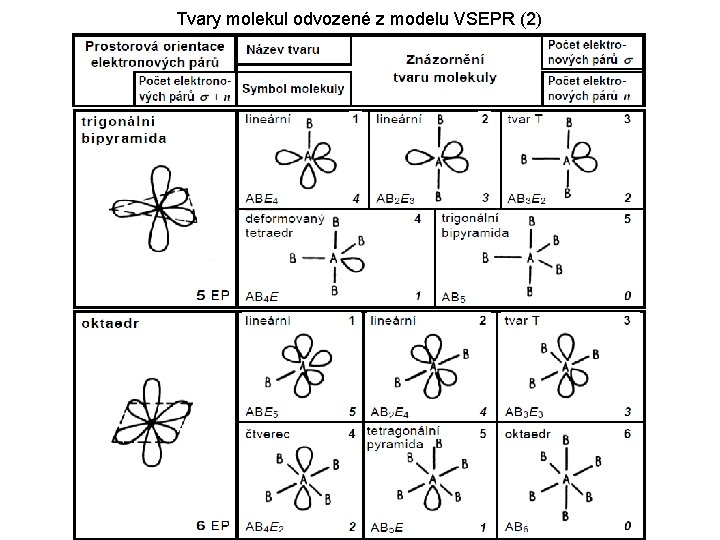
Tvary molekul odvozené z modelu VSEPR (2)

Chemická vazba Vazbou rozumíme obecně interakci mezi atomy nebo molekulami. Podle energie můžeme rozdělit vazebné interakce na tzv. silné a slabé. Z energetického pohledu představují slabé vazebné interakce deset a vícekrát menší energii, nežli ty silné. Silné vazebné interakce představují: – Kovalentní vazbu – Iontovou vazbu – Kovovou vazbu Mezi slabé vazebné interakce pak řadíme: – Van der Wallsovy síly – Vodíkovou vazbu

Charakteristika atomů (molekul) v chemické vazbě – Poloměr atomu (kovalentní, iontový, kovový, Van der Wallsův) a rozložení elektronové hustoty – Elektronová afinita a ionizační potenciál – Elektronegativita – Dipólový moment

Kovalentní vazba – Dokonale kovalentní vazba (mezi atomy se stejnou elektronegativitou) – Polární kovalentní vazba versus vazba iontová – Koordinačně kovalentní (dativní) vazba

Iontová vazba a stavba krystalických látek

Krystaly. . .

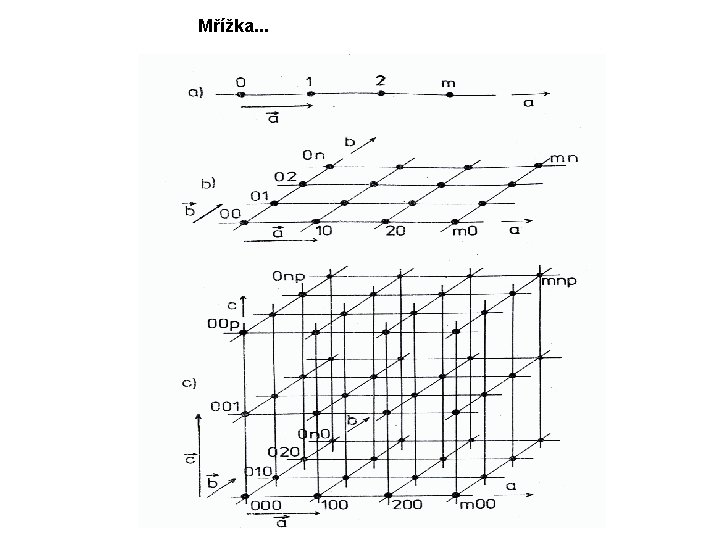
Podle relativní velikosti mřížových parametrů můžeme rozdělit mříže do sedmi krystalových soustav a a a a ≠b≠c; =b=c; =b≠c; =b=c; α , β , γ ≠ 90° α = γ = 90° ; β ≠ 90° α = β = γ = 90° α , β , γ ≠ 90° α = β = 90° ; γ = 120° α = β = γ = 90° Trojklonná Jednoklonná Kosočtverečná Klencová Šesterečná Čtverečná Krychlová

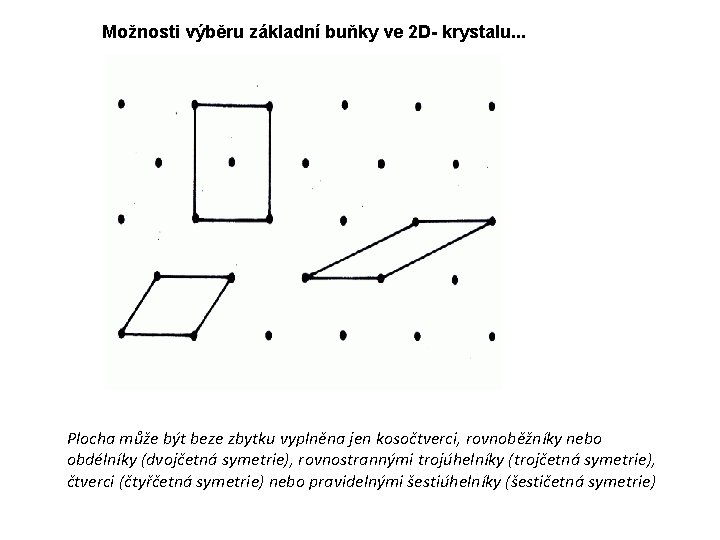
Možnosti výběru základní buňky ve 2 D- krystalu. . . Plocha může být beze zbytku vyplněna jen kosočtverci, rovnoběžníky nebo obdélníky (dvojčetná symetrie), rovnostrannými trojúhelníky (trojčetná symetrie), čtverci (čtyřčetná symetrie) nebo pravidelnými šestiúhelníky (šestičetná symetrie)

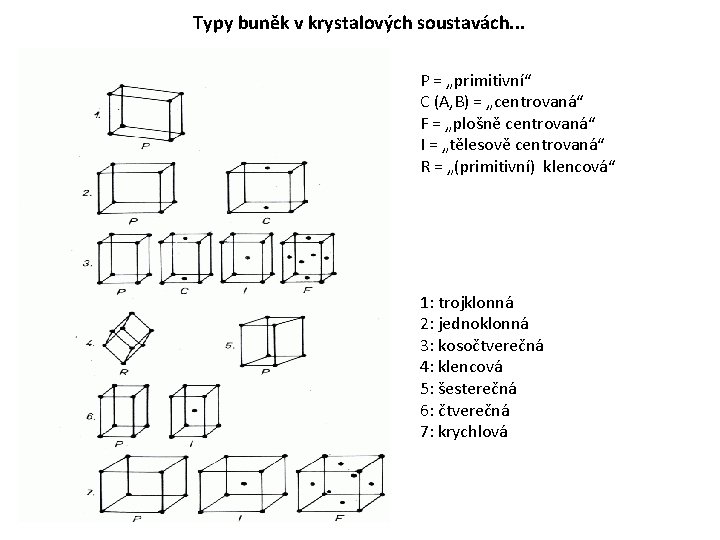
Typy buněk v krystalových soustavách. . . P = „primitivní“ C (A, B) = „centrovaná“ F = „plošně centrovaná“ I = „tělesově centrovaná“ R = „(primitivní) klencová“ 1: trojklonná 2: jednoklonná 3: kosočtverečná 4: klencová 5: šesterečná 6: čtverečná 7: krychlová

Kovová vazba Kovovou vazbou máme na mysli vazbu v kovech, obecně v souborech stejných atomů („koulí o stejné velikosti“). Z krystalografického hlediska umožňuje takové uspořádání jen velmi omezené množství možností. Zjednodušeně můžeme říci, že existují pouze tři způsoby takového uspořádání – tři typy kovových mříží. Z pohledu teorie molekulových orbitalů můžeme na kovový krystal pohlížet jako na molekulu, s obrovským množstvím vazebných, nevazebných a protivazebných orbitalů, jejichž energie se vzájemně liší jen nepatrně, což umožňuje volný pohyb elektronů v molekule (kovovém krystalu). Z pohledu tzv. „pásové struktury“ (viz další obrázek) představují kovy dokonalé překrytí valenčního a vodivostního pásu.

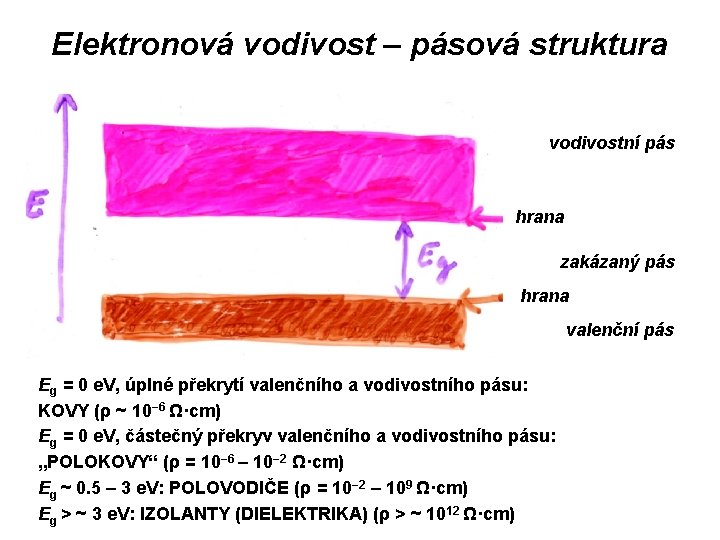
Elektronová vodivost – pásová struktura vodivostní pás hrana zakázaný pás hrana valenční pás Eg = 0 e. V, úplné překrytí valenčního a vodivostního pásu: KOVY (ρ ~ 10− 6 Ω·cm) Eg = 0 e. V, částečný překryv valenčního a vodivostního pásu: „POLOKOVY“ (ρ = 10− 6 – 10− 2 Ω·cm) Eg ~ 0. 5 – 3 e. V: POLOVODIČE (ρ = 10− 2 – 109 Ω·cm) Eg > ~ 3 e. V: IZOLANTY (DIELEKTRIKA) (ρ > ~ 1012 Ω·cm)

Slabé vazebné interakce Van der Wallsovy síly • Interakce dipól – dipól • Interakce dipól – indukovaný dipól • Interakce indukovaný dipól – indukovaný dipól • Dispersní síly

Vodíková vazba „Látky obsahující vodík vázaný na některý z velmi elektronegativních atomů vykazují vlastnosti, které lze nejlépe vysvětlit předpokladem, že vodíkový atom – i když je vázán k danému prvku – má malou, ale významnou afinitu k dalším elektronegativním atomům. Tato poměrně slabá sekundární vazba se nazývá vodíková vazba“ X — H…. Y F. A. Cotton, G. Wilkinson: Anorganická chemie, Academia, Praha 1973

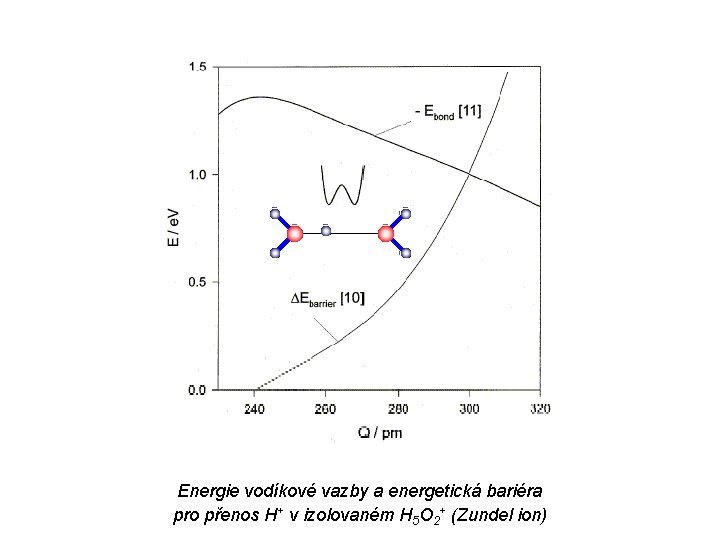
Energie vodíkové vazby a energetická bariéra pro přenos H+ v izolovaném H 5 O 2+ (Zundel ion)