Anonymization Algorithms Other techniques metrics and extended scenarios

Anonymization Algorithms Other techniques, metrics, and extended scenarios Li Xiong CS 573 Data Privacy and Anonymity

So far n k-anonymity (protect identity disclosure) n Anonymization algorithms n Generalization and suppression n Microaggregation and clustering n Privacy principles beyond k-anonymity n l-diversity, t-closeness (protect attribute disclosure) n m-invariance (protect continuous publishing)

Agenda n Other anonymization technique n Anatomization n Information metrics n Extended scenarios

Anonymization methods n Non-perturbative: don't distort the data n Generalization n Suppression n Perturbative: distort the data n Microaggregation/clustering n Additive noise n Anatomization and permutation n De-associate relationship between QID and sensitive attribute

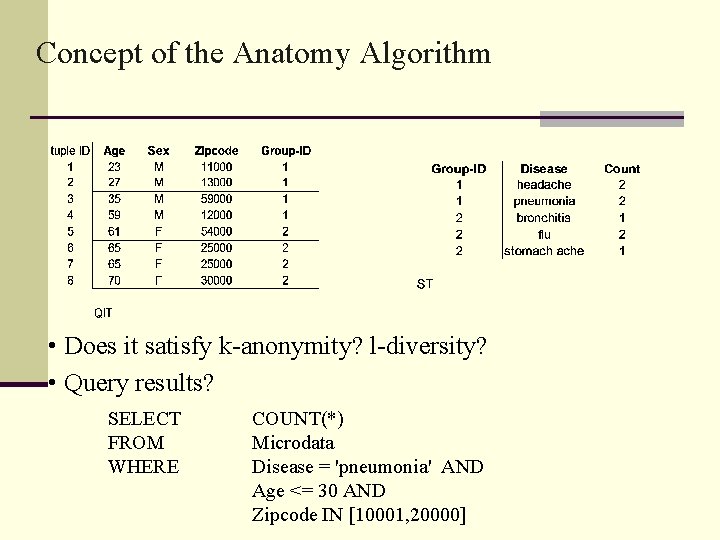
Problems with k-anonymity and l-diversity Query A: SELECT FROM WHERE COUNT(*) Microdata Disease = 'pneumonia' AND Age <= 30 AND Zipcode IN [10001, 20000]

Querying generalized table • • R 1 and R 2 are the anonymized QID groups Q is the query range p = Area(R 1 ∩ RQ)/Area(R 1) = (10*10)/(50*40) = 0. 05 Estimated Answer for A: 2(0. 05) = 0. 1

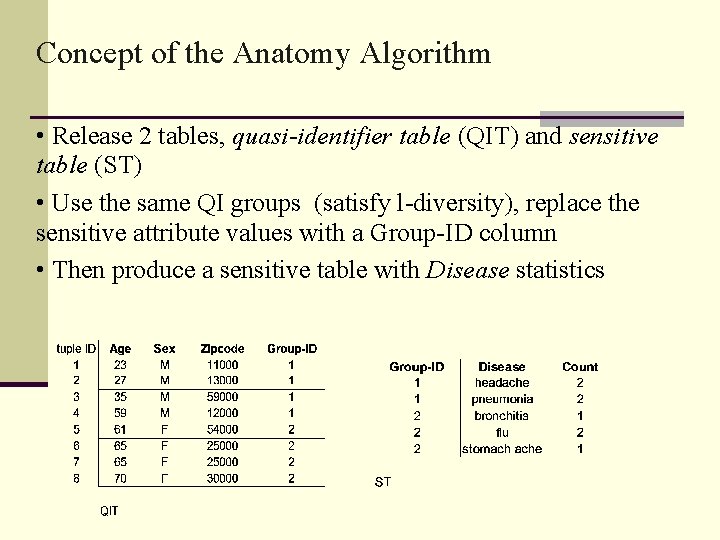
Concept of the Anatomy Algorithm • Release 2 tables, quasi-identifier table (QIT) and sensitive table (ST) • Use the same QI groups (satisfy l-diversity), replace the sensitive attribute values with a Group-ID column • Then produce a sensitive table with Disease statistics

Concept of the Anatomy Algorithm • Does it satisfy k-anonymity? l-diversity? • Query results? SELECT FROM WHERE COUNT(*) Microdata Disease = 'pneumonia' AND Age <= 30 AND Zipcode IN [10001, 20000]

Specifications of Anatomy • T is representation of the microdata to be published • T has d QI attributes Aqi 1, Aqi 2, . . . , Aqid and a sensitive attribute As • Each Aqii (1 ≤ i ≤ d ) is either numerical or categorical, but As can only be categorical because of l-diversity • t is a tuple within T and Aqii is the value of t with [d + 1] as the As value • With the above stated, we can consider t to be a point in a (d +1)-dimensional data space regarded as DS

Specifications of Anatomy cont. DEFINITION 1. (Partition/QI-group) A partition is several subsets of T and only allow each tuple to belong to one subset Subsets are know as QI-groups and are denoted as follows QI 1, QI 2, . . . , QIm

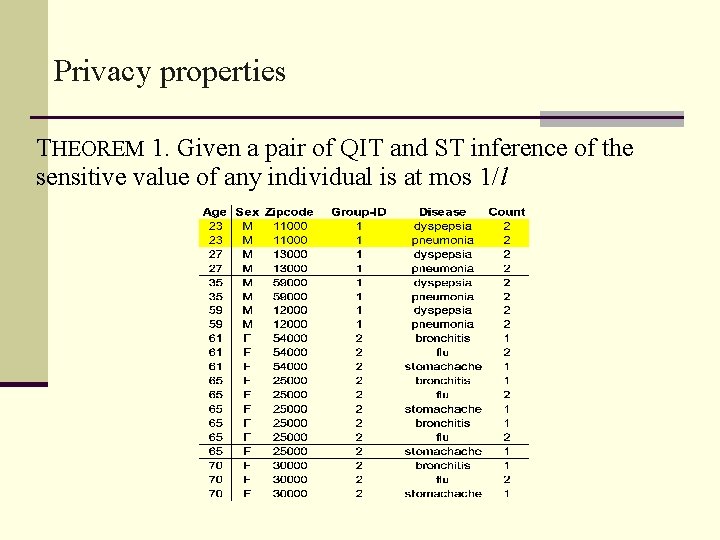
Specifications of Anatomy cont. DEFINITION 2. (l-diverse partition) A partition is considered l-diverse if it conforms to the following: v is the most frequent sensitive value in a QI-group QIj and cj(v) is the number of tuples that match v cj(v)/|QIj| ≤ 1/l |QIj| is the number of tuples of QIj c 1(dyspepsia) = c 1(pneumonia) = 2 and c 2(flu) = 2 |QI 1| = |QI 2| = 4 so this satisfies the condition 2/4 ≤ 1/2

Specifications of Anatomy cont. DEFINITION 3. (Anatomy) With a given l-diverse partition anatomy will create QIT and ST tables QIT will be constructed as the following: (Aqi 1, Aqi 2, . . . , Aqid, Group-ID) ST will be constructed as the following: (Group-ID, As, Count)

Privacy properties THEOREM 1. Given a pair of QIT and ST inference of the sensitive value of any individual is at mos 1/l

Comparison with generalization • Compare with generalization on two assumptions: A 1: the adversary has the QI-values of the target individual A 2: the adversary also knows that the individual is definitely in the microdata If A 1 and A 2 are true, anatomy is as good as generalization 1/l holds true If A 1 is true and A 2 is false, generalization is stronger If A 1 and A 2 are false, generalization is still stronger

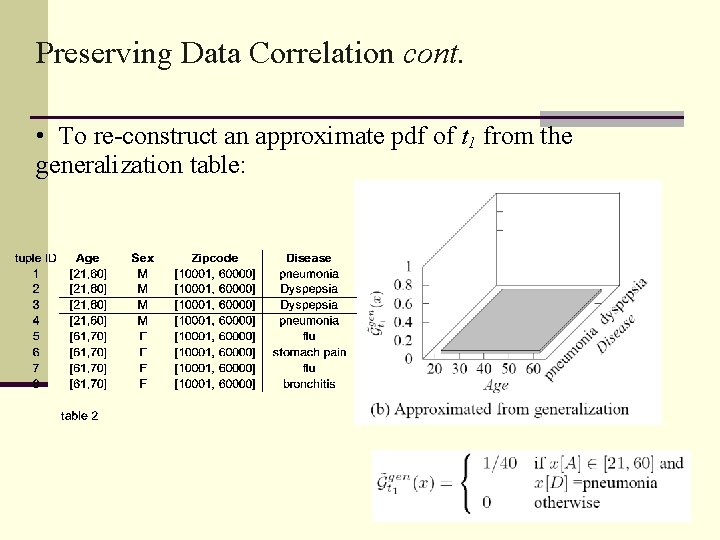
Preserving Data Correlation • Examine the correlation between Age and Disease in T using probability density function pdf • Example: t 1

Preserving Data Correlation cont. • To re-construct an approximate pdf of t 1 from the generalization table:

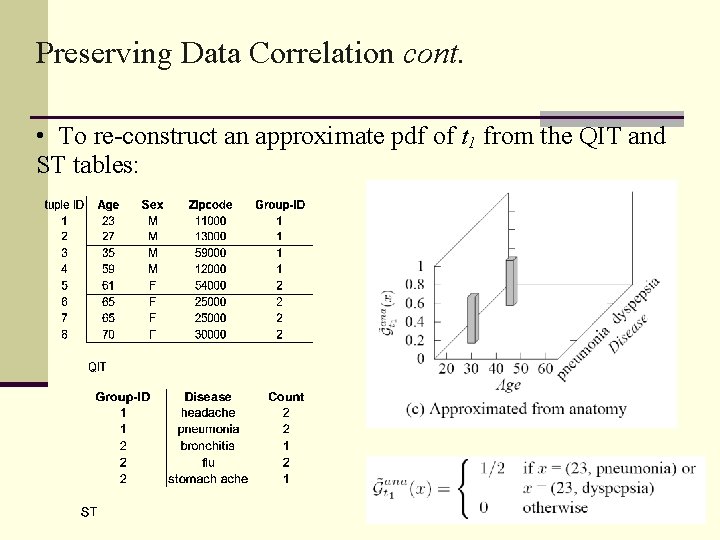
Preserving Data Correlation cont. • To re-construct an approximate pdf of t 1 from the QIT and ST tables:

Preserving Data Correlation cont. • To figure out a more rigorous comparison, calculate the “L 2 distance” with the following equation: The distance for anatomy is 0. 5 while the distance for generalization is 22. 5 • Anatomy provides for better re-constructions of the probability density functions of all tuples.

Preserving Data Correlation cont. • measure the error for each pdf by using the following formula: Objective: for all tuples t in T and obtain a minimal reconstruction error (RCE):

Nearly-Optimal Anatomizing Algorithm • They propose an efficient algorithm for anatomizing tables that will minimize the RCE • The resulting QIT and ST achieves an RCE that only deviates from the lower bound by a factor < 1 + 1/n, where n is the size of T • This algorithm has linear I/O complexity O(n/b) where b is the page size

Nearly-Optimal Anatomizing Algorithm cont. PROPERTY 1. At the end of the group-creation phase, each non-empty bucket has only one tuple. PROPERTY 2. The set S' always includes at least one QI-group. PROPERTY 3. After the residue-assignment phase, each QI group has at least l tuples with distinct senstive attribute value

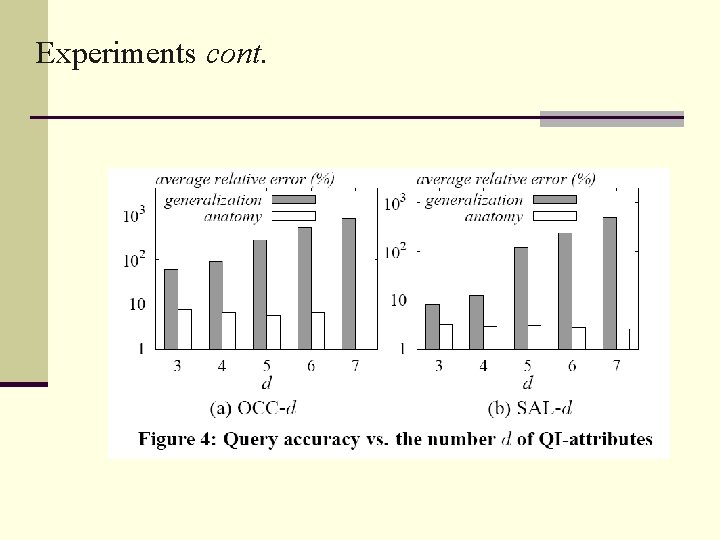
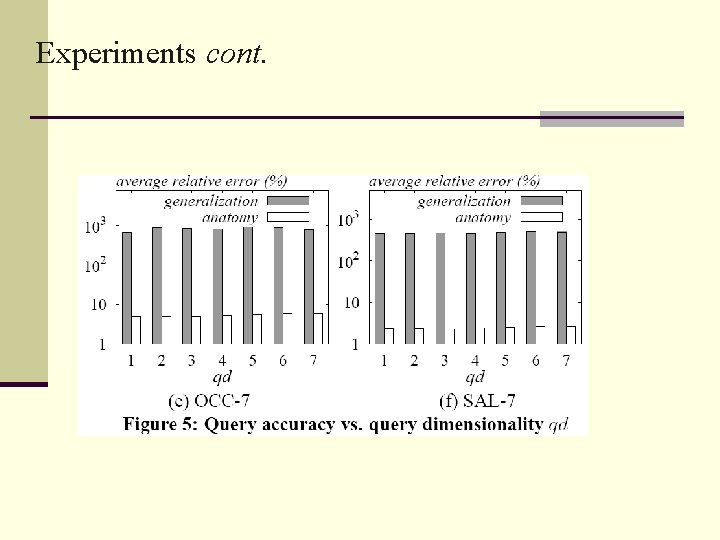
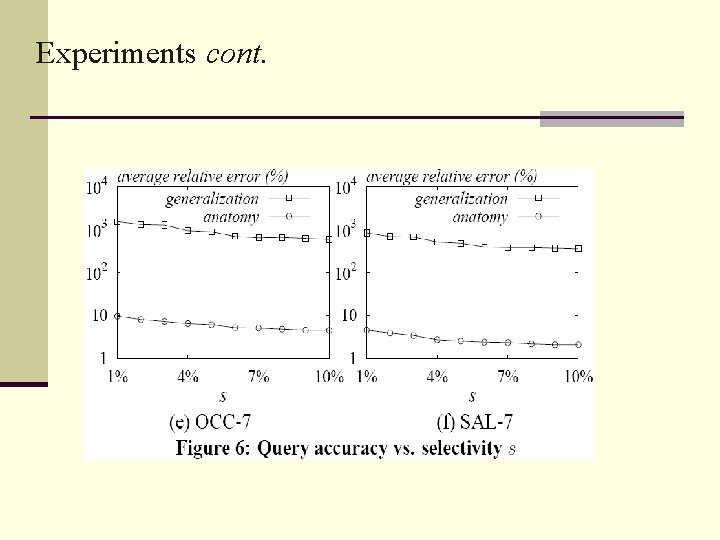
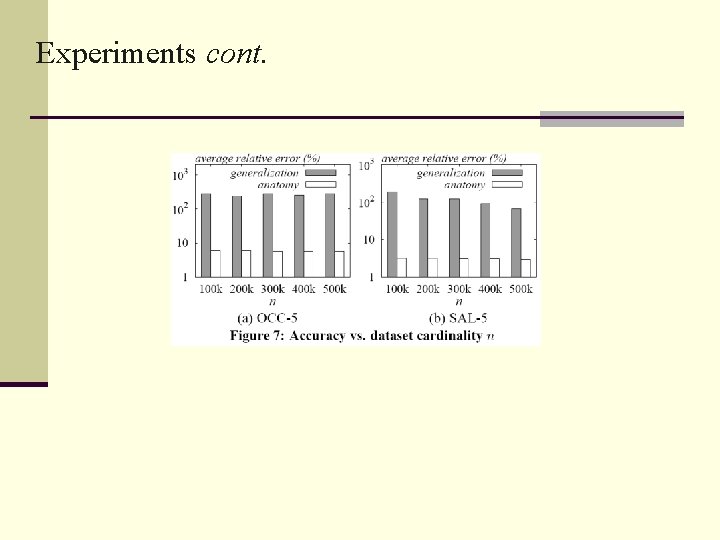
Experiments • dataset CENSUS that contained the personal information of 500 k American adults containing 9 discrete attributes • Created two sets of microdata tables Set 1: 5 tables denoted as OCC-3, . . . , OCC-7 so that OCC-d (3 ≤ d ≤ 7) uses the first d as QI-attributes and Occupation as the sensitive attribute As Set 2: 5 tables denoted as SAL-3, . . . , SAL-7 so that SAL-d (3 ≤ d ≤ 7) uses the first d as QI-attributes and Salary-class as the sensitive attribute As g

Experiments cont.

Experiments cont.

Experiments cont.

Experiments cont.

Conclusion • Anatomy was designed to overcome the problem of generalization of losing too much data and still obtain privacy • Anatomy has a significantly lower error rate as compared with generalization • Several items would require further research - Multiple sensitive attributes - Effective mining of patterns in microdata

Agenda n Other anonymization technique n Anatomization n Information metrics n Extended scenarios

Information Metrics n General purpose metrics n Special purpose metrics n Trade-off metrics

General Purpose Metrics n General idea: measure “similarity” between the original data and the anonymized data n Minimal distortion metric (Samarati 2001; Sweeney 2002, Wang and Fung 2006) n Charge a penalty to each instance of a value generalized or suppressed (independently of other records) n ILoss (Xiao and Tao 2006) n Charge a penalty when a specific value is generalized

General Purpose Metrics cont. n Discernibility Metric (DM) (K-OPTIMIZE, Mondrian, l-diversity …) n Charge a penalty to each record for being indistinguishable from other records

Special Purpose Metrics n Classification: Classification metric (CM) (Iyengar 2002) n Charge a penalty for each record suppressed or generalized to a group in which the record’s class is not the majority class n Query error: count queries n Query imprecision: overlapped range

Extended Scenarios n Multiple release publishing n Continuous release publishing n Collaborative/distributed publishing

Other types of data n High dimensional transaction data n Market basket, web queries n Moving objects data n Location based services n Textual data