Anomalous Hall effect in multiband disordered systems from

Anomalous Hall effect in multiband disordered systems: from the metallic to the hopping regime JAIRO SINOVA Texas A&M University Institute of Physics ASCR Texas A&M University Xiong-Jun Liu, Xin Liu (Nankai) Institute of Physics ASCR Tomas Jungwirth, et al UCLA A. Kovalev, Y. Tserkovnyak Hitachi Cambridge J. Wunderlich, A. Irvine, et al Workshop on Spintronics and Low Dimensional Magnetism June 17 th, 2010 Fudam University, Shanghai, China Research fueled by:

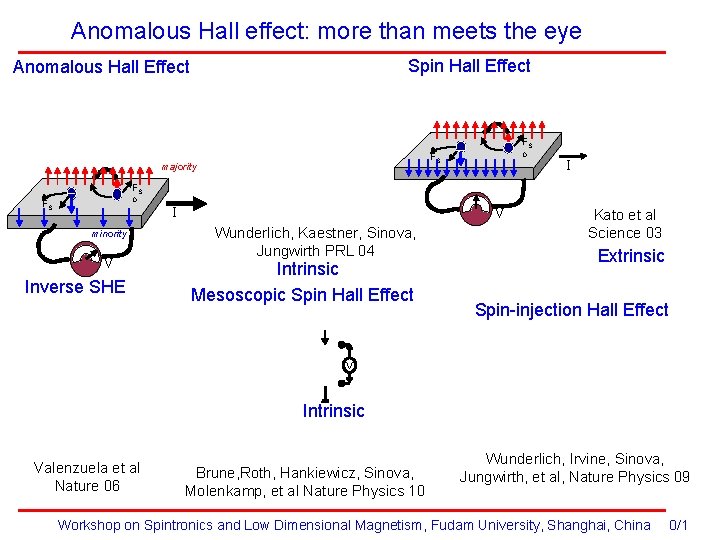
Anomalous Hall effect: more than meets the eye Spin Hall Effect Anomalous Hall Effect _ FS majority _ _ _ FS O O I FS O FS I O minority V Inverse SHE V Wunderlich, Kaestner, Sinova, Jungwirth PRL 04 Intrinsic Mesoscopic Spin Hall Effect Kato et al Science 03 Extrinsic Spin-injection Hall Effect V Intrinsic Valenzuela et al Nature 06 Brune, Roth, Hankiewicz, Sinova, Molenkamp, et al Nature Physics 10 Wunderlich, Irvine, Sinova, Jungwirth, et al, Nature Physics 09 Workshop on Spintronics and Low Dimensional Magnetism, Fudam University, Shanghai, China 0/1

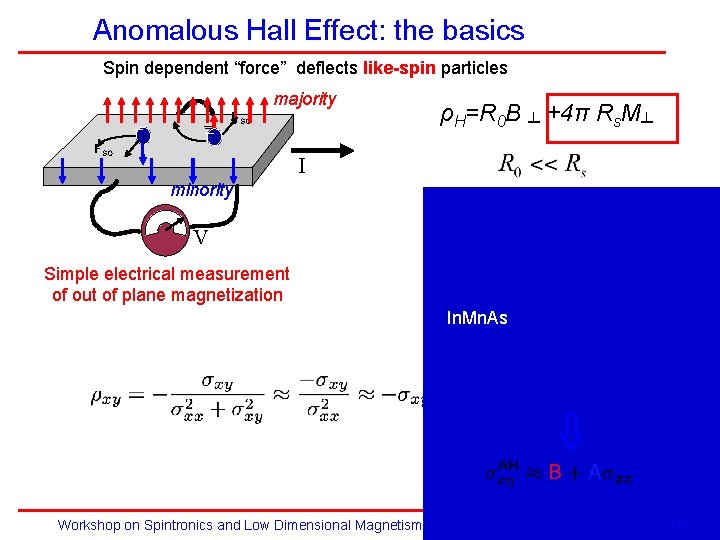
Anomalous Hall Effect: the basics Spin dependent “force” deflects like-spin particles _ __ majority FSO ρH=R 0 B ┴ +4π Rs. M┴ I minority V Simple electrical measurement of out of plane magnetization In. Mn. As Workshop on Spintronics and Low Dimensional Magnetism, Fudam University, Shanghai, China 1/1

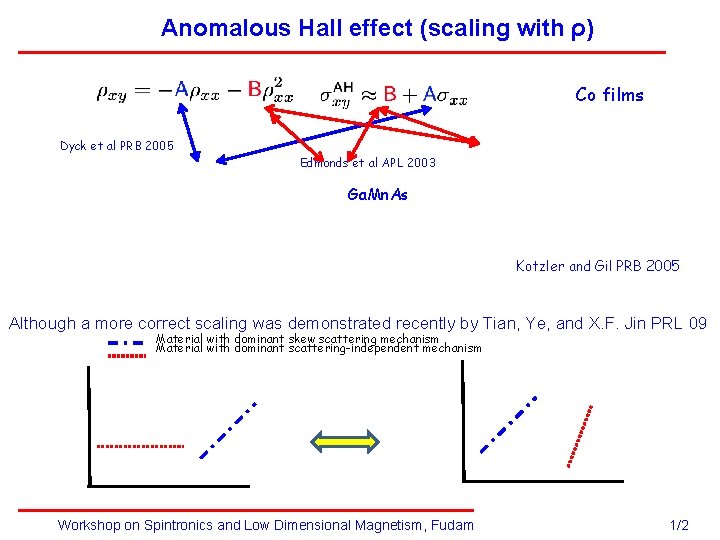
Anomalous Hall effect (scaling with ρ) Co films Dyck et al PRB 2005 Edmonds et al APL 2003 Ga. Mn. As Kotzler and Gil PRB 2005 Although a more correct scaling was demonstrated recently by Tian, Ye, and X. F. Jin PRL 09 Material with dominant skew scattering mechanism Material with dominant scattering-independent mechanism Workshop on Spintronics and Low Dimensional Magnetism, Fudam University, Shanghai, China 1/2

Phenomenological regimes of AHE Review of AHE (RMP 2010), Nagaosa, Sinova, Onoda, Mac. Donald, Ong 1. A high conductivity regime for σxx>106 (Ωcm)-1 in which AHE is skew dominated 2. A good metal regime for σxx ~104 -106 (Ωcm) -1 in which σxy. AH~ const 3. A bad metal/hopping regime for σxx<104 (Ωcm) -1 for which σxy. AH~ σxyα with α>1 Skew dominated regime Workshop on Spintronics and Low Dimensional Magnetism, Fudam University, Shanghai, China 2/3

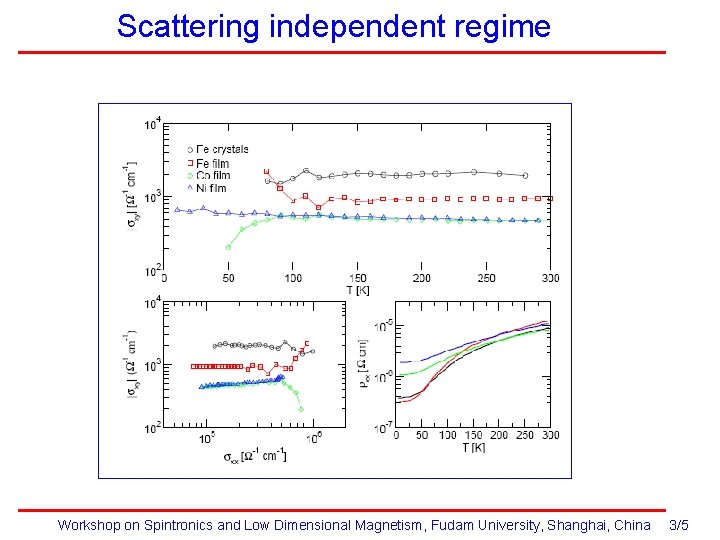
Scattering independent regime Workshop on Spintronics and Low Dimensional Magnetism, Fudam University, Shanghai, China 3/5

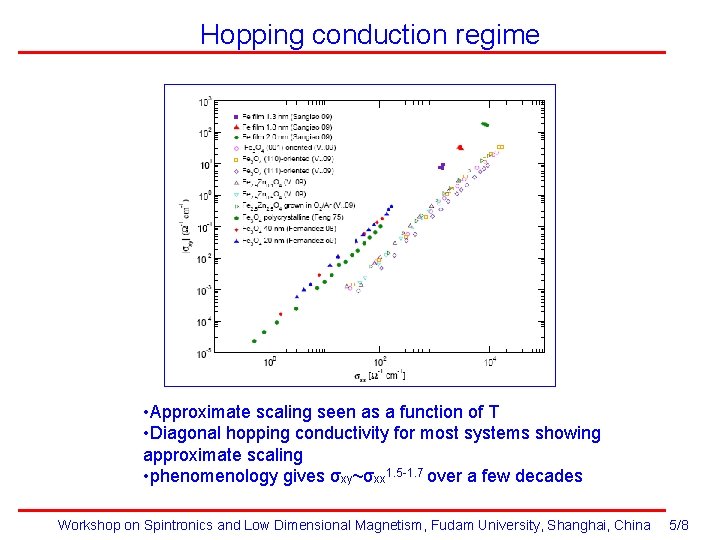
Hopping conduction regime • Approximate scaling seen as a function of T • Diagonal hopping conductivity for most systems showing approximate scaling • phenomenology gives σxy~σxx 1. 5 -1. 7 over a few decades Workshop on Spintronics and Low Dimensional Magnetism, Fudam University, Shanghai, China 5/8

The tumultuous history of AHE • 1880 -81: Hall discovers the Hall and the anomalous Hall effect • 1954: Karplus and Luttinger attempt first microscopic theory: Hall they develop (and later Kohn and Luttinger) a microscopic theory of linear response transport based on the equation of motion of the density matrix for noninteracting electrons, ; run into problems interpreting results since some terms are gauge dependent. Lack of easy physical connection. • 1955 -58: Smit attempts to create a semi-classical theory using wavepackets formed from Bloch band states: identifies the skew scattering and Luttinger notices a side-step of the wave-packet upon scattering and accelerating. . Speculates, wrongly, that the side-step cancels to zero. The physical interpretation of the cancellation is based on a gauge dependent object!! • 1970: Berger reintroduces (and renames) the side-jump: claims that it does not vanish and that it is the dominant contribution, ignores intrinsic contribution. (problem: his side-jump is gauge dependent) • 1970’s: Berger, Smit, and others argue about the existence of side-jump: the field is left in a confused state. Who is right? How can we tell? Three contributions to Berger AHE are floating in the literature of the AHE: anomalous velocity (intrinsic), side-jump, and skew contributions. • 1972 -87: Detailed quantitative by Fert and Levy understanding of resonant skew scattering: paramagnetic systems with imbedded magnetic impurities (d and f). 5/8

The tumultuous history of AHE: last three decades • 1980’s: Ideas of geometric phases introduced by Berry; QHE discoveries • 2000’s: Materials with strong spin-orbit coupling show agreement with the anomalous velocity contribution: intrinsic contribution linked to Berry’s curvature of Bloch states. Ignores disorder contributions. • 2004’s: Spin-Hall effect is revived by the proposal of intrinsic SHE (from two works working on intrinsic AHE): AHE comes to the masses, many debates are inherited in the discussions of SHE. • 2004 -10’s: Linear theories in simple models treating SO coupling and disorder finally merge: full semi-classical theory developed and microscopic approaches are in agreement among each other in simple models. • 2010: More detailed ab-initio studies and formalism developed for metals; hopping regime begins to be understood 8/13

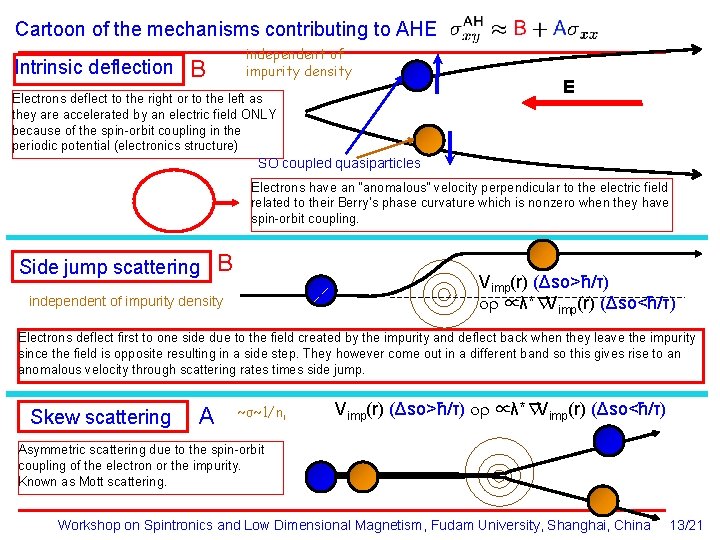
Cartoon of the mechanisms contributing to AHE Intrinsic deflection independent of impurity density B Electrons deflect to the right or to the left as they are accelerated by an electric field ONLY because of the spin-orbit coupling in the periodic potential (electronics structure) E SO coupled quasiparticles Electrons have an “anomalous” velocity perpendicular to the electric field related to their Berry’s phase curvature which is nonzero when they have spin-orbit coupling. Side jump scattering B Vimp(r) (Δso>ħ/τ) or ∝λ*∇Vimp(r) (Δso<ħ/τ) independent of impurity density Electrons deflect first to one side due to the field created by the impurity and deflect back when they leave the impurity since the field is opposite resulting in a side step. They however come out in a different band so this gives rise to an anomalous velocity through scattering rates times side jump. Skew scattering A ~σ~1/ni Vimp(r) (Δso>ħ/τ) or ∝λ*∇Vimp(r) (Δso<ħ/τ) Asymmetric scattering due to the spin-orbit coupling of the electron or the impurity. Known as Mott scattering. Workshop on Spintronics and Low Dimensional Magnetism, Fudam University, Shanghai, China 13/21

Microscopic vs. Semiclassical • Boltzmann semiclassical approach: easy physical interpretation of different contributions (used to define them) but very easy to miss terms and make mistakes. Must be confirmed microscopically. How one understands but not necessarily computes the effect. • Kubo approach: systematic formalism but not very transparent. • Keldysh approach: also a systematic kinetic equation approach (equivalent to Kubo in the linear regime). In the quasi-particle limit it must yield Boltzmann semiclassical treatment. Workshop on Spintronics and Low Dimensional Magnetism, Fudam University, Shanghai, China 21/34

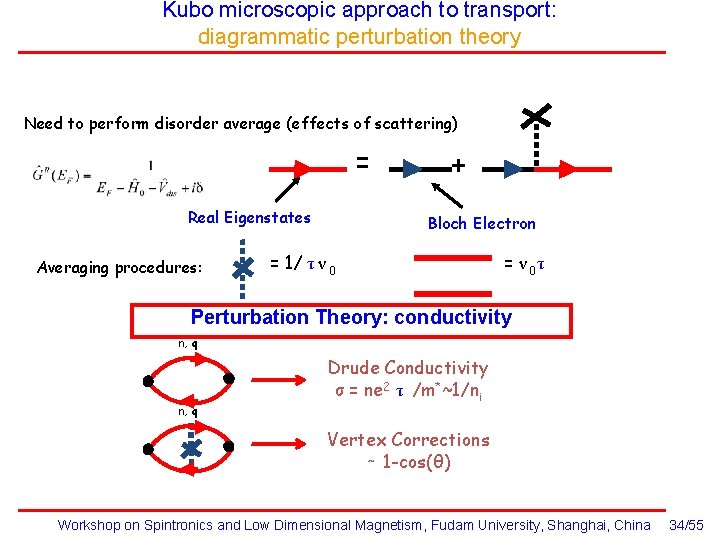
Kubo microscopic approach to transport: diagrammatic perturbation theory Need to perform disorder average (effects of scattering) = Real Eigenstates Averaging procedures: + Bloch Electron = 1/ τ ν 0 = ν 0τ Perturbation Theory: conductivity n, q Drude Conductivity σ = ne 2 τ /m*~1/ni Vertex Corrections ∼ 1 -cos(θ) Workshop on Spintronics and Low Dimensional Magnetism, Fudam University, Shanghai, China 34/55

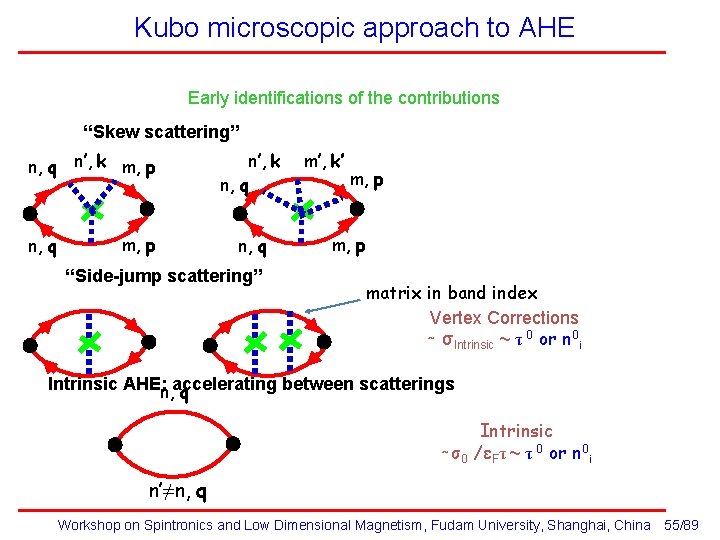
Kubo microscopic approach to AHE Early identifications of the contributions “Skew scattering” n, q n’, k m, p n, q m, p n’, k n, q “Side-jump scattering” m’, k’ m, p matrix in band index Vertex Corrections ∼ σIntrinsic ~ τ 0 or n 0 i Intrinsic AHE: n, accelerating between scatterings q Intrinsic ∼ σ0 /εFτ ~ τ 0 or n 0 i n’≠n, q Workshop on Spintronics and Low Dimensional Magnetism, Fudam University, Shanghai, China 55/89

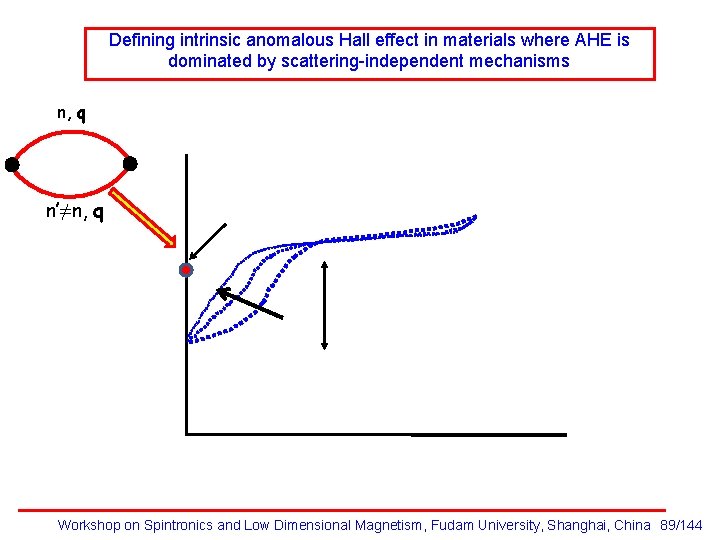
Defining intrinsic anomalous Hall effect in materials where AHE is dominated by scattering-independent mechanisms n, q n’≠n, q Workshop on Spintronics and Low Dimensional Magnetism, Fudam University, Shanghai, China 89/144

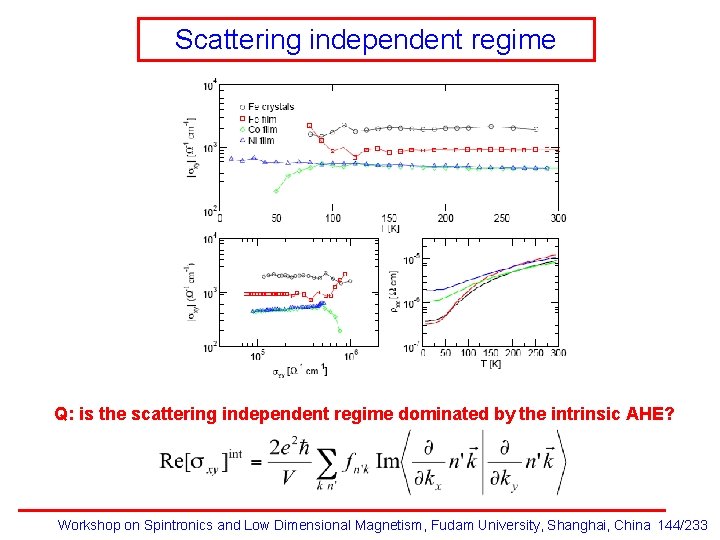
Scattering independent regime Q: is the scattering independent regime dominated by the intrinsic AHE? Workshop on Spintronics and Low Dimensional Magnetism, Fudam University, Shanghai, China 144/233

n, q n’≠n, q intrinsic AHE approach in comparing to experiment: phenomenological “proof” • DMS systems (Jungwirth et al PRL 2002, APL 03) • Fe (Yao et al PRL 04) • layered 2 D ferromagnets such as Sr. Ru. O 3 and pyrochlore ferromagnets [Onoda et al (2001), Taguchi et al. , AHE in Ga. Mn. As Science 291, 2573 (2001), Fang et al Science 302, 92 (2003) • colossal magnetoresistance of manganites, Ye et~al Phys. AHE in Fe Rev. Lett. 83, 3737 (1999). • Cu. Cr. Se. Br compounts, Lee et al, Science 303, 1647 (2004) Experiment σ AH ∼ 1000 (Ω cm)-1 Theroy σ AH ∼ 750 (Ω cm)-1 Workshop on Spintronics and Low Dimensional Magnetism, Fudam University, Shanghai, China 233/377

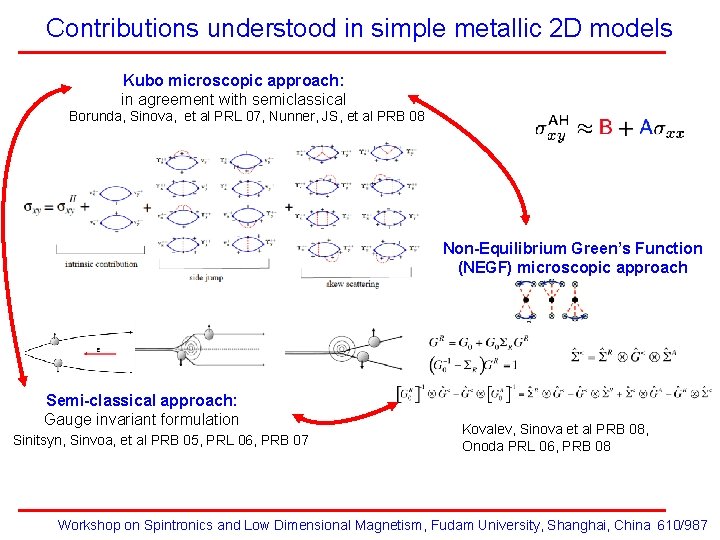
Contributions understood in simple metallic 2 D models Kubo microscopic approach: in agreement with semiclassical Borunda, Sinova, et al PRL 07, Nunner, JS, et al PRB 08 Non-Equilibrium Green’s Function (NEGF) microscopic approach Semi-classical approach: Gauge invariant formulation Sinitsyn, Sinvoa, et al PRB 05, PRL 06, PRB 07 Kovalev, Sinova et al PRB 08, Onoda PRL 06, PRB 08 Workshop on Spintronics and Low Dimensional Magnetism, Fudam University, Shanghai, China 610/987

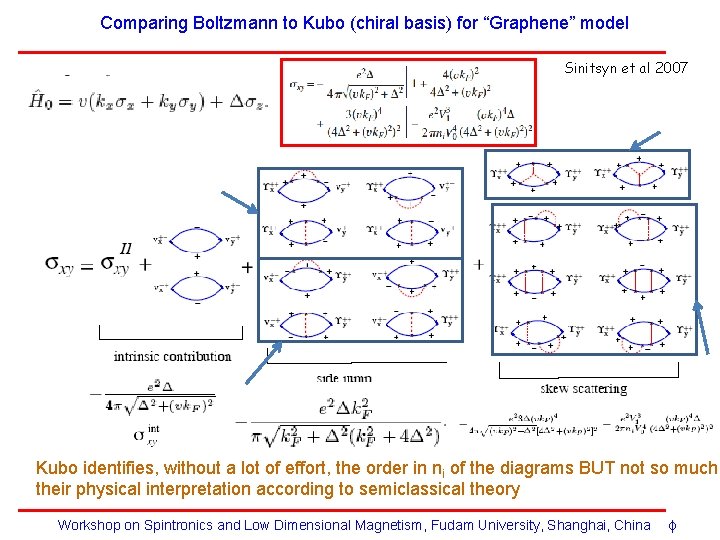
Comparing Boltzmann to Kubo (chiral basis) for “Graphene” model Sinitsyn et al 2007 Kubo identifies, without a lot of effort, the order in ni of the diagrams BUT not so much their physical interpretation according to semiclassical theory Workshop on Spintronics and Low Dimensional Magnetism, Fudam University, Shanghai, China ϕ

Generalization to 3 D General band structure in the presence of delta-correlated Gaussian disorder N-band projected Hamiltonian expressed via envelope fields In the presence of Gaussian disorder To test our theory we will consider band structures of a 2 D Rashba and 3 D Luttinger models: 6 -band Luttinger model will also be considered Kovalev, Sinova, Tserkovnyak PRL 2010 Workshop on Spintronics and Low Dimensional Magnetism, Fudam University, Shanghai, China 1/4

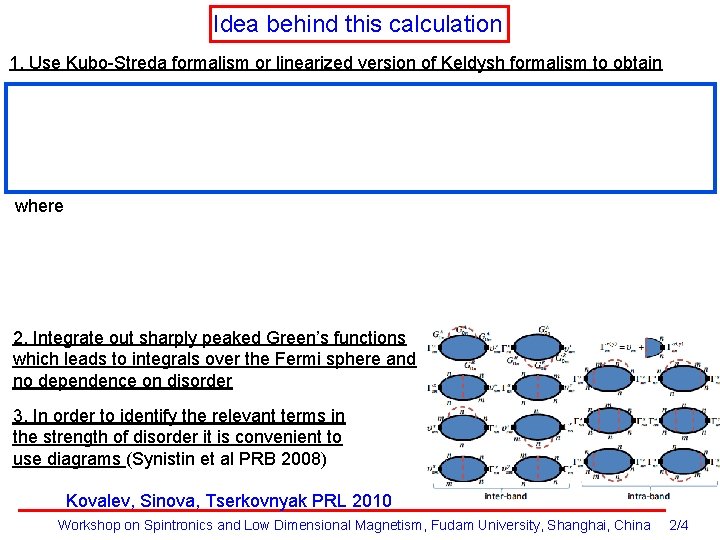
Idea behind this calculation 1. Use Kubo-Streda formalism or linearized version of Keldysh formalism to obtain where 2. Integrate out sharply peaked Green’s functions which leads to integrals over the Fermi sphere and no dependence on disorder 3. In order to identify the relevant terms in the strength of disorder it is convenient to use diagrams (Synistin et al PRB 2008) Kovalev, Sinova, Tserkovnyak PRL 2010 Workshop on Spintronics and Low Dimensional Magnetism, Fudam University, Shanghai, China 2/4

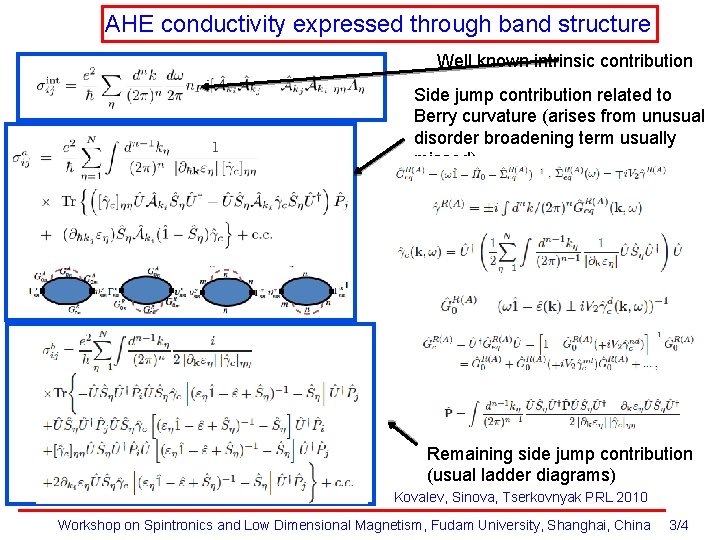
AHE conductivity expressed through band structure Well known intrinsic contribution Side jump contribution related to Berry curvature (arises from unusual disorder broadening term usually missed) Remaining side jump contribution (usual ladder diagrams) Kovalev, Sinova, Tserkovnyak PRL 2010 Workshop on Spintronics and Low Dimensional Magnetism, Fudam University, Shanghai, China 3/4

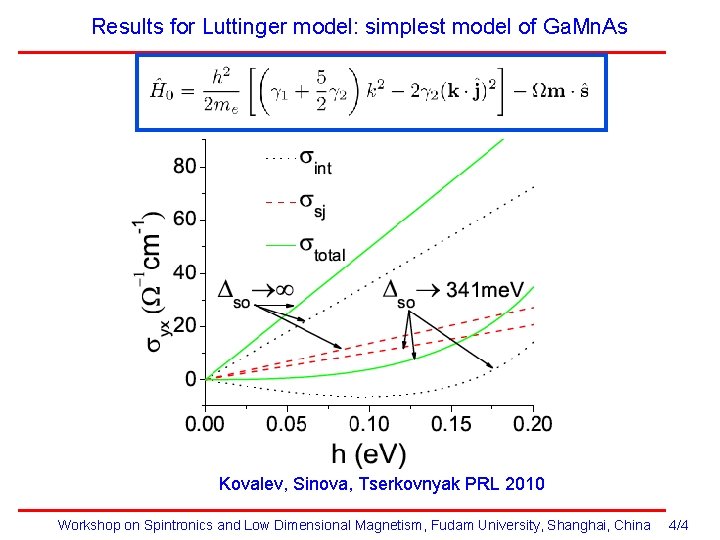
Results for Luttinger model: simplest model of Ga. Mn. As Kovalev, Sinova, Tserkovnyak PRL 2010 Workshop on Spintronics and Low Dimensional Magnetism, Fudam University, Shanghai, China 4/4

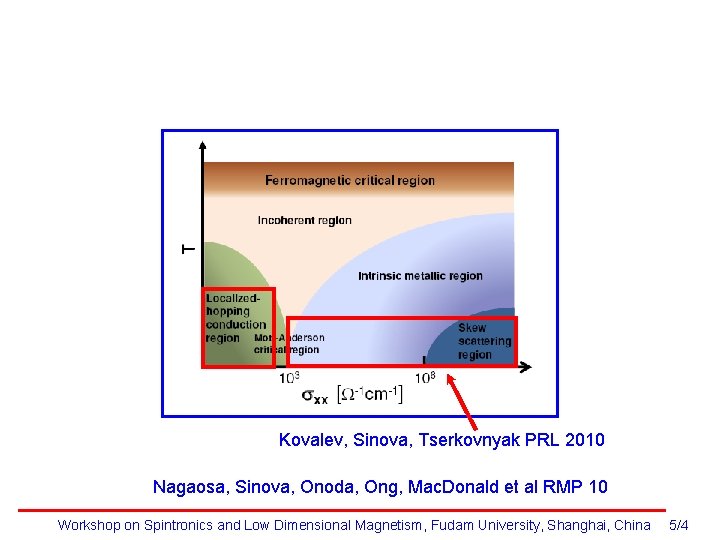
Kovalev, Sinova, Tserkovnyak PRL 2010 Nagaosa, Sinova, Onoda, Ong, Mac. Donald et al RMP 10 Workshop on Spintronics and Low Dimensional Magnetism, Fudam University, Shanghai, China 5/4

Anomalous Hall effect in the hopping regime Three regimes of anomalous Hall effect 1. Intrinsic regime: 2. Skew scattering: 3. Hopping regime: This scaling relation has been seen in many experiments: B. A. Aronzon etal. , phys. stat. sol. (b) 218, 169 (2000) W. Allen, etal. , Phys. Rev. B 70, 125320 (2004) . . H. Toyosaki etal. , Nature, 3, 221 (2004) K. Ueno etal. , Appl. Phys. Lett. 90, 072103 (2007) T. Miyasato etal. , Phys. Rev. Lett. , 99, 086602 (2007) D. Venkateshvaran etal. , Phys. Rev. B 78, 092405 (2008) A. Fernández-Pacheco etal. , Phys. Rev. B 77, 100403(R) (2008) Previous Theories: S. H. Chun etal. , Phys. Rev. Lett. 84, 757 (2000), A. A. Burkov and L. Balents, Phys. Rev. Lett. 91, 057202 (2003), Cannot explain the scaling relation in the experiment. Workshop on Spintronics and Low Dimensional Magnetism, Fudam University, Shanghai, China 1/9

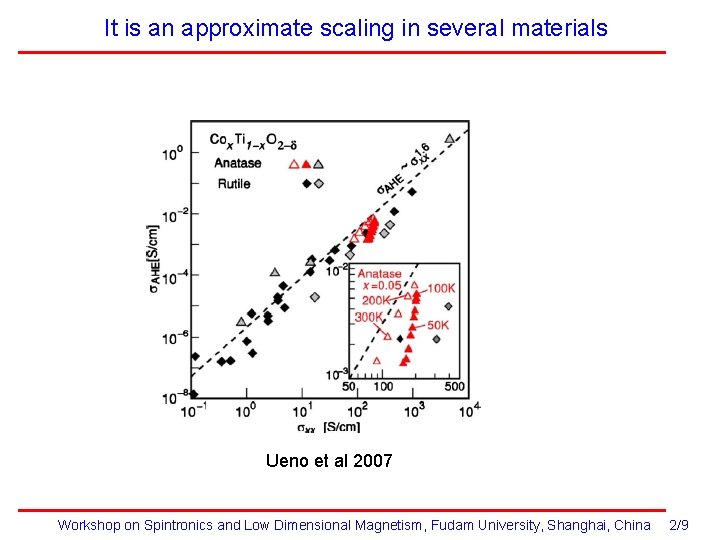
It is an approximate scaling in several materials Ueno et al 2007 Workshop on Spintronics and Low Dimensional Magnetism, Fudam University, Shanghai, China 2/9

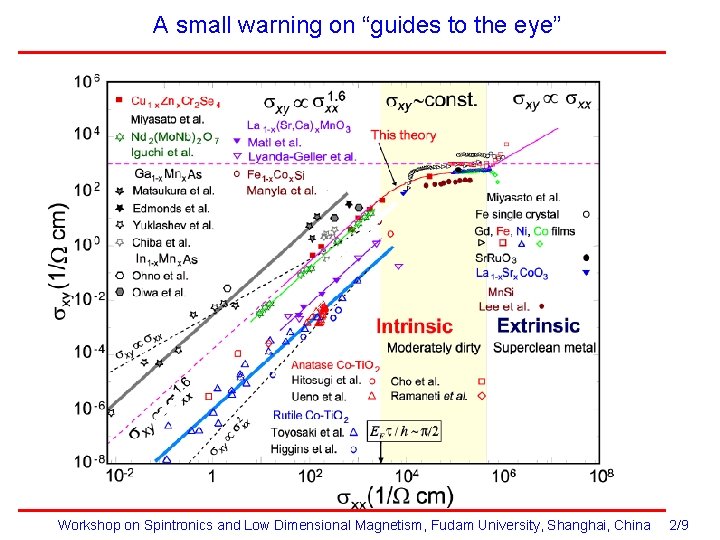
A small warning on “guides to the eye” Workshop on Spintronics and Low Dimensional Magnetism, Fudam University, Shanghai, China 2/9

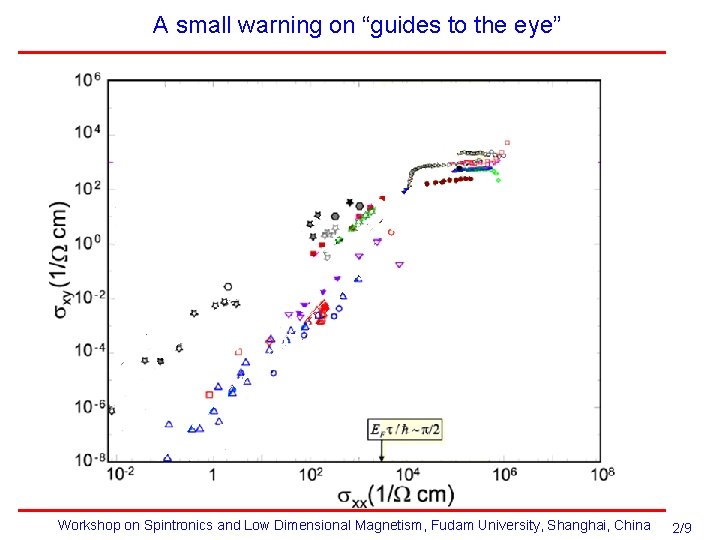
A small warning on “guides to the eye” Workshop on Spintronics and Low Dimensional Magnetism, Fudam University, Shanghai, China 2/9

Phonon-assisted hopping between localized states The Hamiltonian describing localized states and e-ph interaction (Holstein 1961, Burkov etal, 2003) with phonon Localization: phonon-assisted hopping i j k Electric current between two sites: Ri : direct conductance due to two-site hopping. Rk Rj : off-diagonal conductance due to three-site hopping. Workshop on Spintronics and Low Dimensional Magnetism, Fudam University, Shanghai, China 3/9

Perturbative method to calculate the Hall conductivity Recall the charge current: Perturbation method for the present triad: a) First step: applying the external electric field, neglecting the Hall current, then calculating the voltage of each node according to the Kirchoff’s equation: The Hall current through each node is then calculated with the voltage obtained in the first step: b) Second step: turning off the electric field, and considering only above calculated Hall current flowing through each node. One can then calculate the Hall current between each two sites, and the corresponding Hall voltage, with which one can finally obtain the Hall conductivity. Workshop on Spintronics and Low Dimensional Magnetism, Fudam University, Shanghai, China 4/9

Perturbative method to calculate the Hall conductivity (II) For example, we calculate the Hall current flowing between site 2 and 3. For this we first derive the voltage difference between them due to the present current situation: 3 The corresponding field is: 1 2 Then the Hall current flowing between site 2 and site 3 is given by: Recall the original current when the external electric field is applied: Workshop on Spintronics and Low Dimensional Magnetism, Fudam University, Shanghai, China 5/9

Linear response to the electric field The charge current in the presence of external electric field is given by: Transverse voltage with and Responsible for the normal conductivity yields zero when the magnetization is zero Responsible for the Hall conductivity: arises from interference of two phonon hopping process Workshop on Spintronics and Low Dimensional Magnetism, Fudam University, Shanghai, China 6/9

Percolation theory For each two site, a bond that can conduct electricity establishes when the direct conductance between them is no less than a critical value (Ambegaokar et al. , 1971): This gives the condition: Ri Rj connected Ri Rj disconnected For a site with energy given by: , the average number of sites connecting to it satisfying above condition is Workshop on Spintronics and Low Dimensional Magnetism, Fudam University, Shanghai, China 7/9

Anomalous Hall conductivity via percolation theory in hopping regime Critical paths appear when the average number : The macroscopic AH conductivity/resistivity should be averaged along the critical path: Instead of exactly calculating the above extremely complicated integral, we shall evaluate its two limits: the lower limit and upper limit, which will be more meaningful. This is because, in the insulating regime, the system is very complicated and the relation between normal and Hall conductivity cannot be uniquely determined by a few parameters. Therefore, in this regime it is more reasonable to consider the scaling relation between them has a range. Xiong-Jun Liu, Sinova 2010 Workshop on Spintronics and Low Dimensional Magnetism, Fudam University, Shanghai, China 8/9

The lower and upper limits are given by (note the differences in the constrain) For the Mott variable range hopping, we find Physically, the upper limit (γ=1. 34) corresponds to the situation that most triads in the system are equilateral triangles (this is actually a regular distribution), while for the lower limit (γ=1. 68) the geometry of triads is randomly distributed. Since the impurity sites are randomly distributed, we expect the realistic result is usually close to the lower limit. This is true for the experiment. Xiong-Jun Liu, Sinova, 2010 Workshop on Spintronics and Low Dimensional Magnetism, Fudam University, Shanghai, China 9/9

SUMMARY • AHE general theory for metallic multi-band systems which contains all scattering-independent contributions developed: useful for ab-initio studies (Kovalev, Sinova, Tserkovnyak PRL 2010) • AHE hopping regime approximate scaling arises directly from a generalization of the Holstein theory to AHE (Xiong-Jun Liu, Sinova 2010) • AHE hopping regime scaling remains even when crossing to different types of insulating hopping regimes, only algebraic pre-factor changes Workshop on Spintronics and Low Dimensional Magnetism, Fudam University, Shanghai, China 10/9

Liviu Zarbo Ewelina Hankiewicz Texas A&M Univ. (Texas A&M Univ. ) ASCR Würzburg University Mario Borunda Texas A&M Univ. Harvard Univ. Xin Liu Texas A&M U. Alexey Kovalev Texas A&M U. UCLA Principal Collaborators Tomas Jungwirth Texas A&M U. Inst. of Phys. ASCR U. of Nottingham Allan Mac. Donald U of Texas Xiong-Jun Liu Texas A&M U. Nikolai Sinitsyn Texas A&M U. U. of Texas LANL Laurens Molenkamp Bryan Gallagher Y. Tserkovnyak Gerrit Bauer Joerg Wunderlich U. of Nottingham UCLA Würzburg TU Delft Cambridge-Hitachi Nanoelectronics, spintronics, and materials control by spin-orbit coupling 36