Announcements Assignment 7 due now or tommorrow Assignment

Announcements • Assignment 7 due now or tommorrow • Assignment 8 posted – Due Friday 25 th. • All project components arrived? • Dates – Thursday 12/1 review lecture – Tuesday 12/6 project demonstrations in the lab (no presentations) – Sunday 12/11 project reports due to me by email – Tuesday 12/13 final exam, 1 pm-3 pm here.

Lecture 21 Overview • More Sequential Logic Design – Another counter example – “don’t care” conditions – Ant Brain Example

FSM Design Procedure • Start with counters • Simple because the output is just the state • Simple because there is no choice of next state based on inputs • Draw the finite state diagram • State diagram to state transition table • Tabular form of state diagram • Similar to a truth-table • State encoding: how do you represent the state in binary? • Decide on representation of states (e. g. traffic light green = what in binary? ) • For counters it is simple: just its value • Implementation • Flip-flop for each state bit • Use Karnaugh maps to find combinational logic, based on state encoding

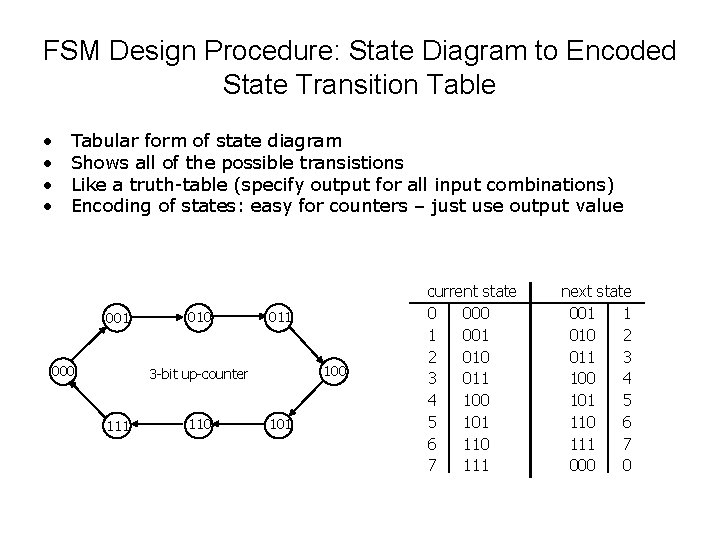
FSM Design Procedure: State Diagram to Encoded State Transition Table • • Transition table is just a tabular form of the state diagram Shows all of the possible transitions Like a truth-table (specify output for all input combinations) Encoding of states: easy for counters – just use output value 001 1 000 0 010 2 011 3 100 4 3 -bit up-counter 111 7 110 6 101 5 current state 0 000 1 001 2 010 3 011 4 100 5 101 6 110 7 111 next state 001 1 010 2 011 3 100 4 101 5 110 6 111 7 000 0

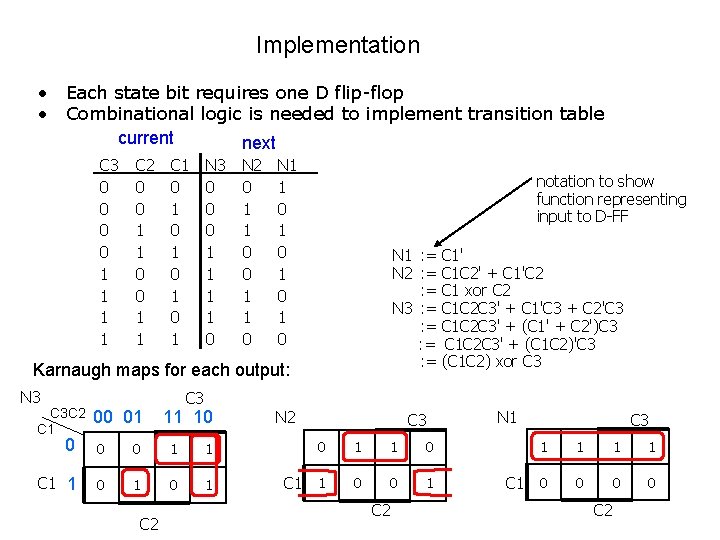
FSM Design Procedure: State Diagram to Encoded State Transition Table • • Tabular form of state diagram Shows all of the possible transistions Like a truth-table (specify output for all input combinations) Encoding of states: easy for counters – just use output value 001 000 011 100 3 -bit up-counter 111 110 101 current state 0 000 1 001 2 010 3 011 4 100 5 101 6 110 7 111 next state 001 1 010 2 011 3 100 4 101 5 110 6 111 7 000 0

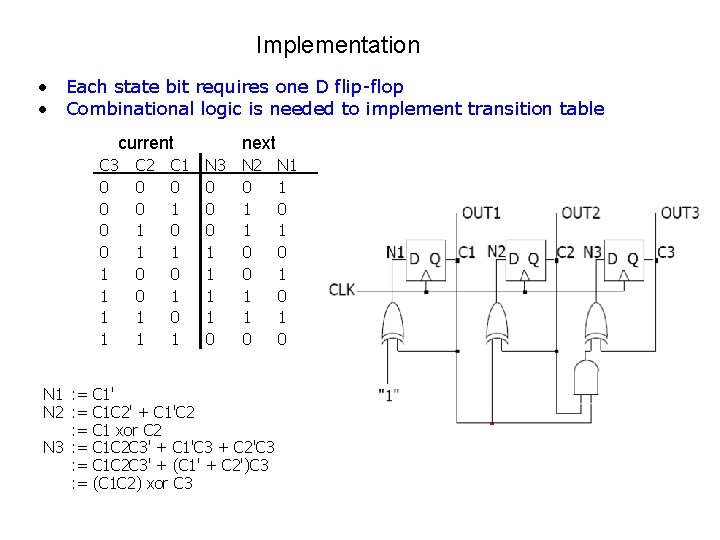
Implementation • Each state bit requires one D flip-flop • Combinational logic is needed to implement transition table current next C 3 0 0 1 1 C 2 0 0 1 1 C 1 0 1 0 1 N 3 0 0 0 1 1 0 N 2 0 1 1 0 N 1 1 0 1 0 notation to show function representing input to D-FF N 1 : = C 1' N 2 : = C 1 C 2' + C 1'C 2 : = C 1 xor C 2 N 3 : = C 1 C 2 C 3' + C 1'C 3 + C 2'C 3 : = C 1 C 2 C 3' + (C 1' + C 2')C 3 : = C 1 C 2 C 3' + (C 1 C 2)'C 3 : = (C 1 C 2) xor C 3 Karnaugh maps for each output: N 3 C 3 C 2 C 1 00 01 C 3 11 10 N 2 C 3 N 1 C 3 0 0 0 1 1 C 1 1 0 1 C 1 1 0 0 1 C 1 0 0 C 2 C 2

Implementation • Each state bit requires one D flip-flop • Combinational logic is needed to implement transition table current C 3 0 0 1 1 C 2 0 0 1 1 C 1 0 1 0 1 next N 3 0 0 0 1 1 0 N 2 0 1 1 0 N 1 : = C 1' N 2 : = C 1 C 2' + C 1'C 2 : = C 1 xor C 2 N 3 : = C 1 C 2 C 3' + C 1'C 3 + C 2'C 3 : = C 1 C 2 C 3' + (C 1' + C 2')C 3 : = (C 1 C 2) xor C 3 N 1 1 0 1 0

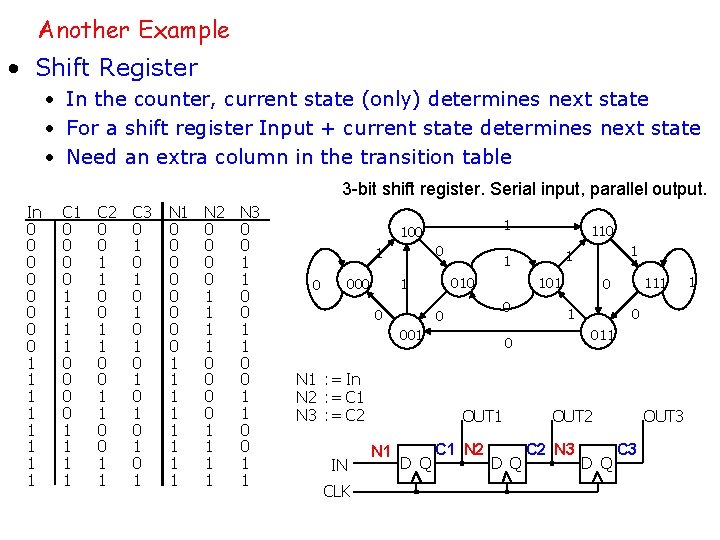
Another Example • Shift Register • In the counter, current state (only) determines next state • For a shift register Input + current state determines next state • Need an extra column in the transition table 3 -bit shift register. Serial input, parallel output. In 0 0 0 0 1 1 1 1 C 1 0 0 0 0 1 1 1 1 C 2 0 0 1 1 C 3 0 1 0 1 N 1 0 0 0 0 1 1 1 1 N 2 0 0 0 0 1 1 1 1 N 3 0 0 1 1 1 100 0 101 0 0 001 N 1 : = In N 2 : = C 1 N 3 : = C 2 IN CLK D Q C 1 N 2 D Q 111 0 011 0 OUT 1 N 1 1 010 1 000 110 OUT 2 C 2 N 3 D Q OUT 3 C 3 1

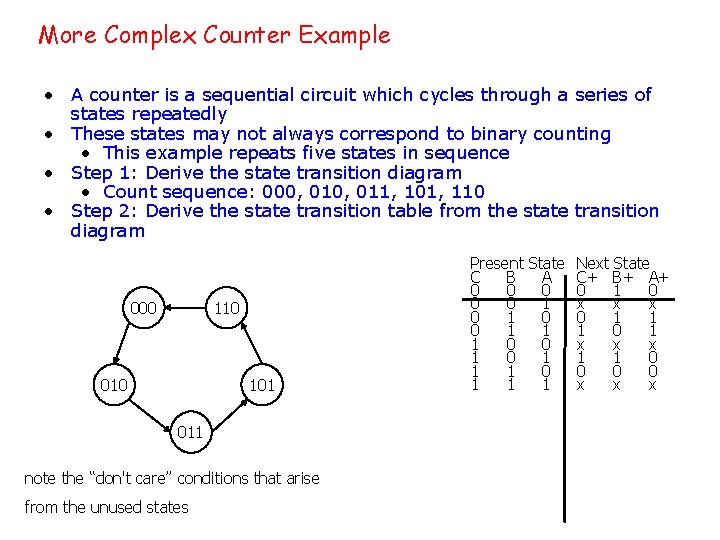
More Complex Counter Example • A counter is a sequential circuit which cycles through a series of states repeatedly • These states may not always correspond to binary counting • This example repeats five states in sequence • Step 1: Derive the state transition diagram • Count sequence: 000, 011, 101, 110 • Step 2: Derive the state transition table from the state transition diagram 000 110 010 101 011 note the “don't care” conditions that arise from the unused states Present State Next State C B A C+ B+ A+ 0 0 1 0 0 0 1 x x x 0 1 0 0 1 1 1 0 0 x x x 1 0 1 1 0 0 1 1 1 x x x

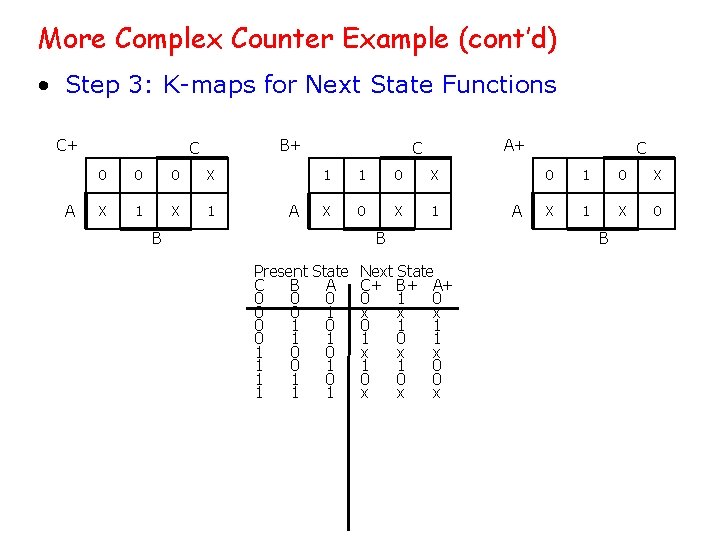
More Complex Counter Example (cont’d) • Step 3: K-maps for Next State Functions C+ A B+ C 0 0 0 X X 1 B A A+ C 1 1 0 X X 0 X 1 B Present State Next State C B A C+ B+ A+ 0 0 1 0 0 0 1 x x x 0 1 0 0 1 1 1 0 0 x x x 1 0 1 1 0 0 1 1 1 x x x A C 0 1 0 X X 1 X 0 B

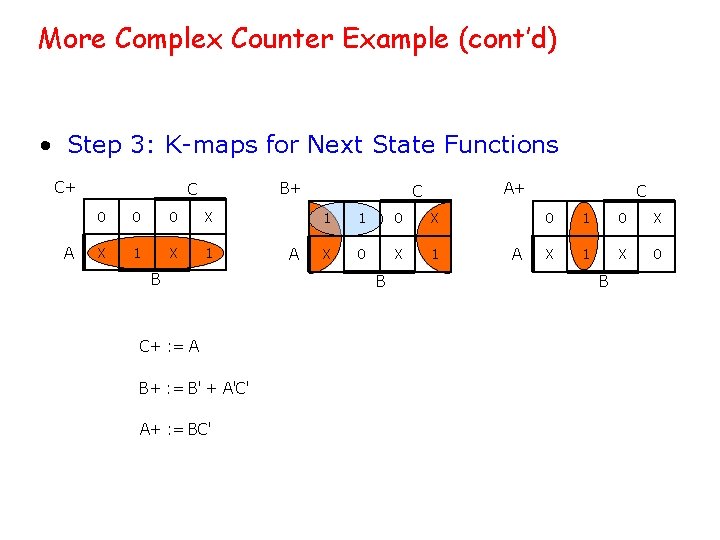
More Complex Counter Example (cont’d) • Step 3: K-maps for Next State Functions C+ A B+ C 0 0 0 X X 1 B C+ : = A B+ : = B' + A'C' A+ : = BC' A A+ C 1 1 0 X X 0 X 1 B A C 0 1 0 X X 1 X 0 B

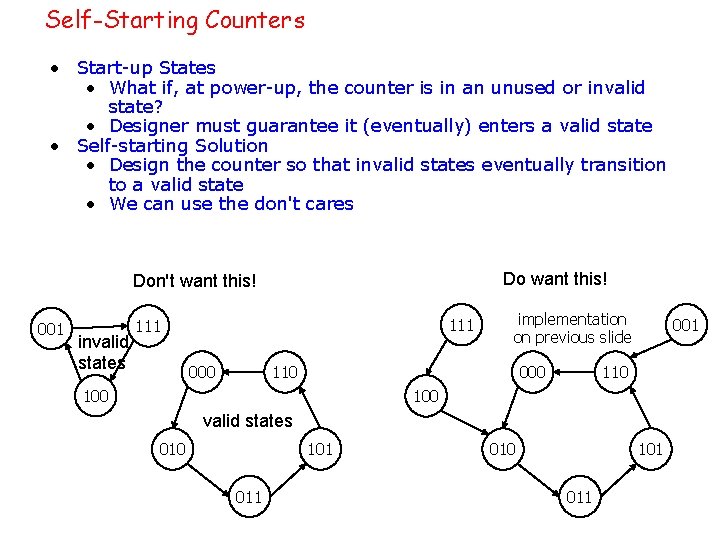
Self-Starting Counters • Start-up States • What if, at power-up, the counter is in an unused or invalid state? • Designer must guarantee it (eventually) enters a valid state • Self-starting Solution • Design the counter so that invalid states eventually transition to a valid state • We can use the don't cares Do want this! Don't want this! 001 invalid states 111 000 implementation on previous slide 110 000 100 001 110 100 valid states 010 101 011

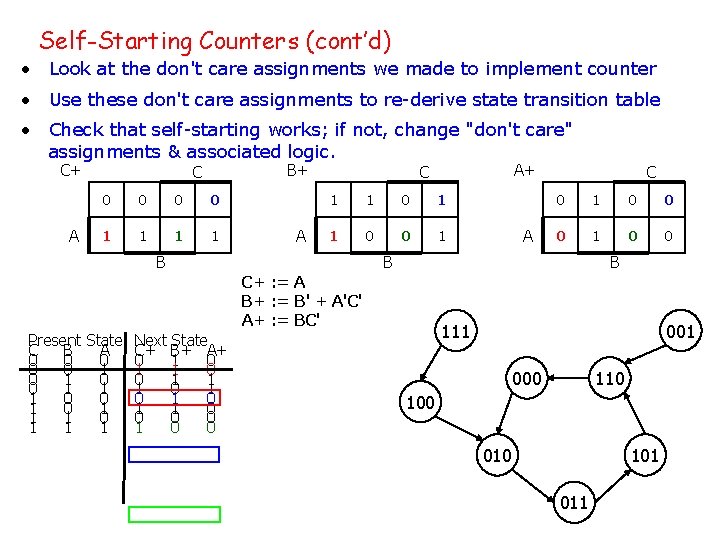
Self-Starting Counters (cont’d) • Look at the don't care assignments we made to implement counter • Use these don't care assignments to re-derive state transition table • Check that self-starting works; if not, change "don't care" assignments & associated logic. C+ A B+ C 0 0 1 1 A 1 1 0 0 1 B A C 0 1 0 0 B B C+ : = A B+ : = B' + A'C' A+ : = BC' Present State Next State C B A C+ B+ A+ 0 0 1 0 0 0 1 1 1 0 0 1 1 0 0 0 1 0 1 1 1 0 0 0 0 1 1 0 0 A+ C 111 000 110 100 010 101 011

Your turn • Design a 3 -bit binary up counter that only counts odd numbers using D-type flipflops. Any even number resets the circuit to 111 • The steps are: • • Draw the state diagram Derive the transition table Use Karnaugh maps to work out the logic Convert this to a circuit

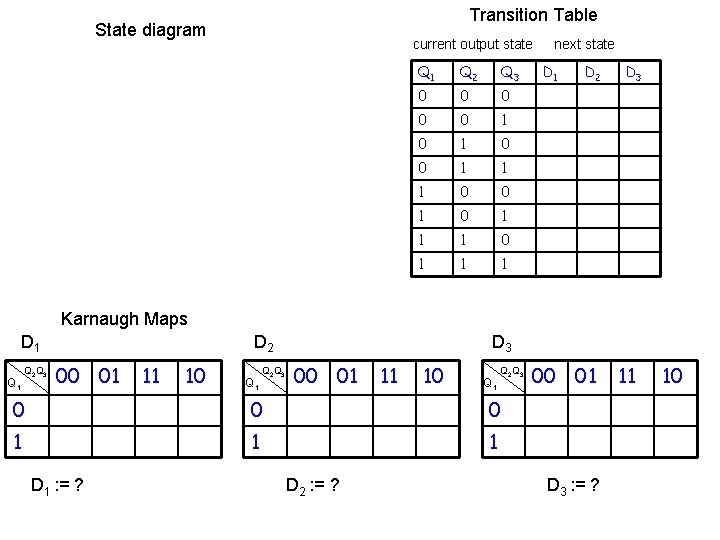
Transition Table State diagram current output state Q 1 Q 2 Q 3 0 0 0 1 1 1 0 0 1 1 1 next state D 1 D 2 D 3 Karnaugh Maps D 1 Q 2 Q 3 D 2 00 01 11 10 Q 1 Q 2 Q 3 D 3 00 01 11 10 Q 1 Q 2 Q 3 0 0 0 1 1 1 D 1 : = ? D 2 : = ? 00 01 D 3 : = ? 11 10

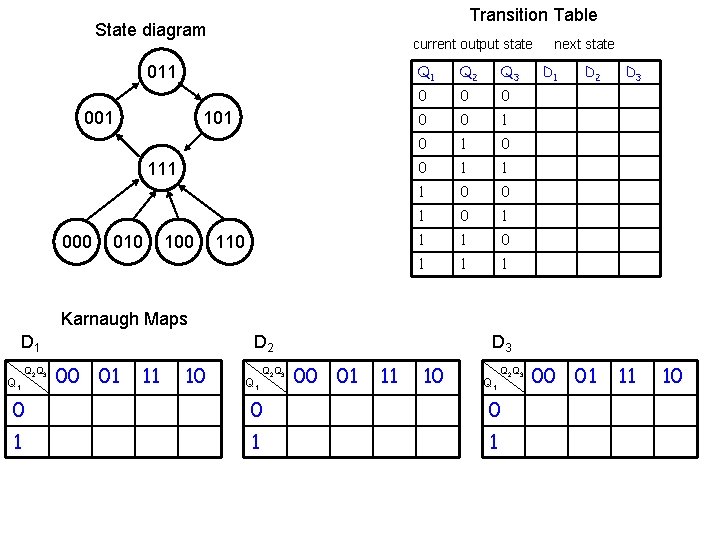
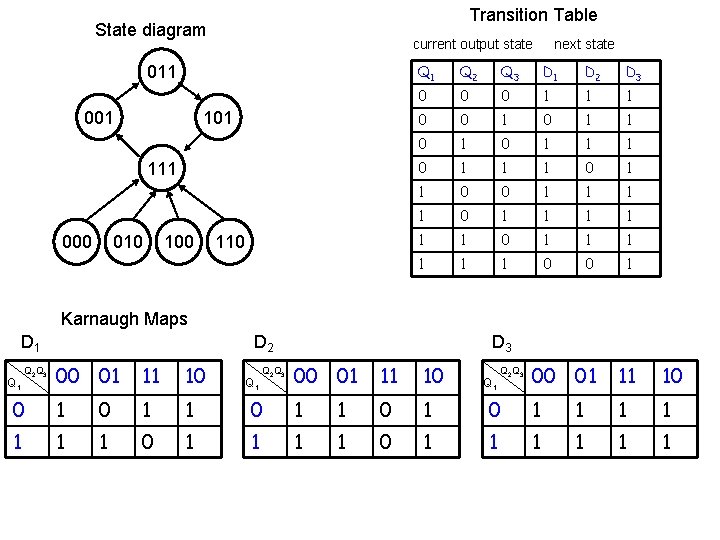
Transition Table State diagram current output state 011 001 111 000 010 100 110 Q 1 Q 2 Q 3 0 0 0 1 1 1 0 0 1 1 1 next state D 1 D 2 D 3 Karnaugh Maps D 1 Q 2 Q 3 D 2 00 01 11 10 Q 1 Q 2 Q 3 D 3 00 01 11 10 Q 1 Q 2 Q 3 0 0 0 1 1 1 00 01 11 10

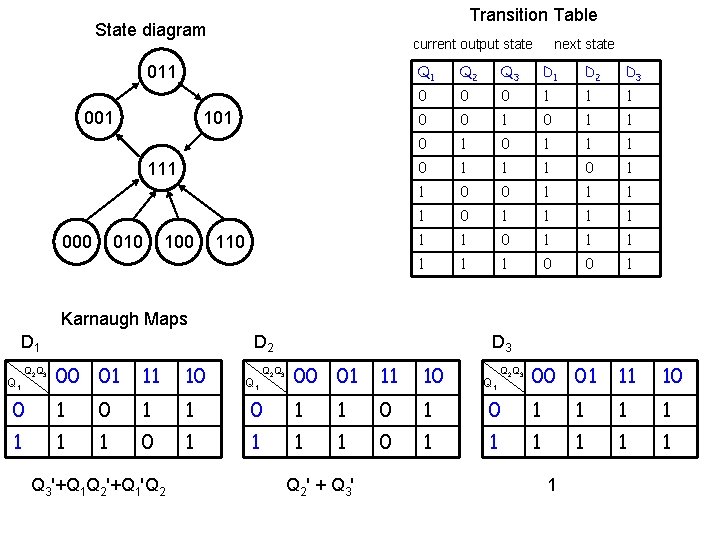
Transition Table State diagram current output state 011 001 111 000 010 100 110 next state Q 1 Q 2 Q 3 D 1 D 2 D 3 0 0 0 1 1 1 0 0 1 0 1 1 0 0 1 1 1 0 1 1 1 0 0 1 00 01 11 10 Karnaugh Maps D 1 D 2 00 01 11 10 0 1 1 1 0 1 Q 2 Q 3 D 3 00 01 11 10 0 1 1 1 1 0 1 1 1 Q 1 Q 2 Q 3

Transition Table State diagram current output state 011 001 111 000 010 100 110 next state Q 1 Q 2 Q 3 D 1 D 2 D 3 0 0 0 1 1 1 0 0 1 0 1 1 0 0 1 1 1 0 1 1 1 0 0 1 00 01 11 10 Karnaugh Maps D 1 D 2 00 01 11 10 0 1 1 1 0 1 Q 2 Q 3 Q 3'+Q 1 Q 2'+Q 1'Q 2 D 3 00 01 11 10 0 1 1 1 1 0 1 1 1 Q 1 Q 2 Q 3 Q 2 ' + Q 3 ' Q 1 Q 2 Q 3 1

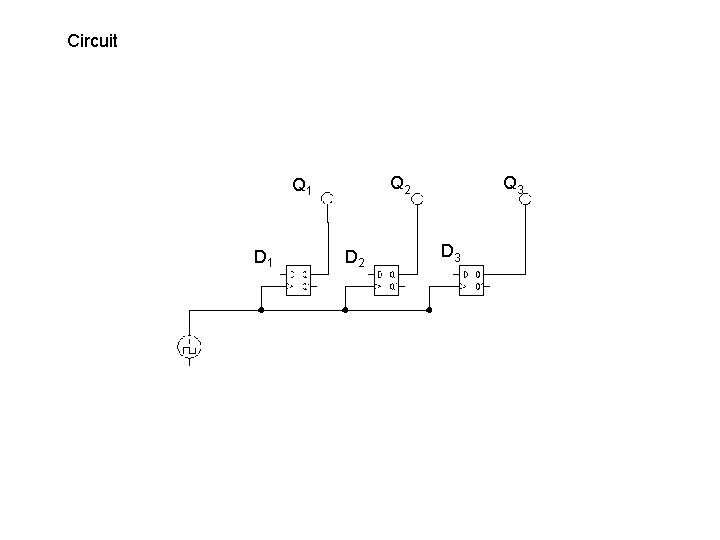
Circuit Q 2 Q 1 D 2 Q 3 D 3

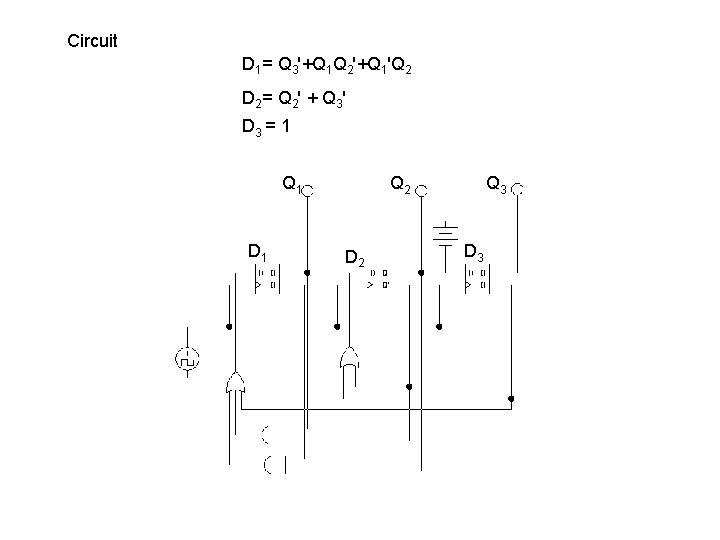
Circuit D 1= Q 3'+Q 1 Q 2'+Q 1'Q 2 D 2 = Q 2 ' + Q 3 ' D 3 = 1 Q 1 D 1 Q 2 D 2 Q 3 D 3

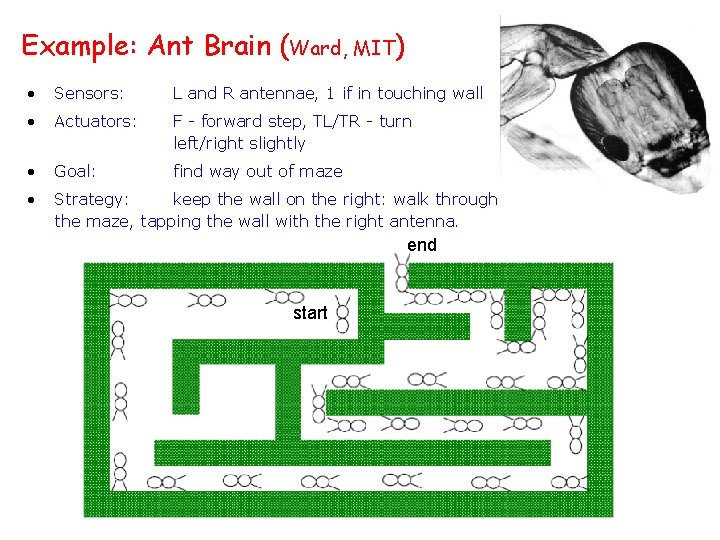
Example: Ant Brain (Ward, MIT) • Sensors: L and R antennae, 1 if in touching wall • Actuators: F - forward step, TL/TR - turn left/right slightly • Goal: find way out of maze • Strategy: keep the wall on the right: walk through the maze, tapping the wall with the right antenna. end start

Ant Brain: Defining the states • We need to turn the strategy into an algorithm - define a series of states and the appropriate response to them. • Special case I : Left antenna touching the wall • Turn 180 degrees - turn left until right antenna no longer touches the wall.

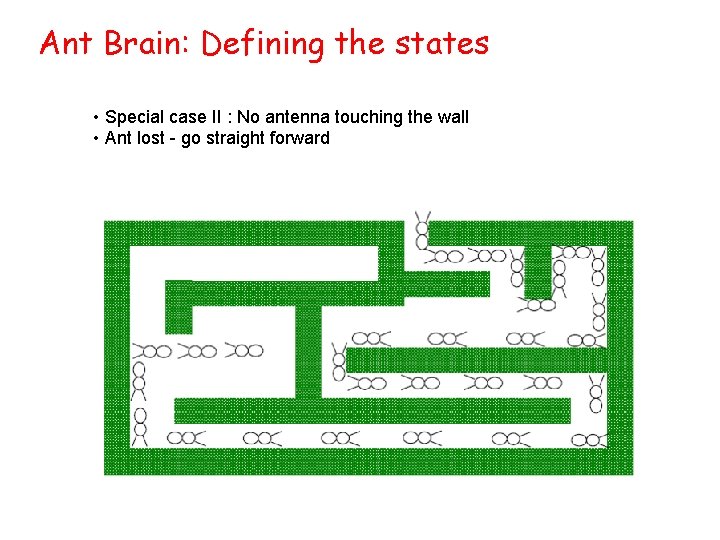
Ant Brain: Defining the states • Special case II : No antenna touching the wall • Ant lost - go straight forward

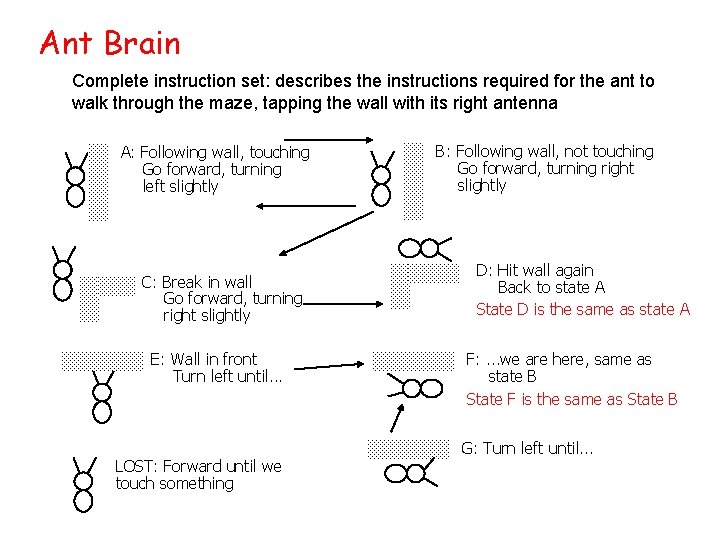
Ant Brain Complete instruction set: describes the instructions required for the ant to walk through the maze, tapping the wall with its right antenna A: Following wall, touching Go forward, turning left slightly C: Break in wall Go forward, turning right slightly E: Wall in front Turn left until. . . LOST: Forward until we touch something B: Following wall, not touching Go forward, turning right slightly D: Hit wall again Back to state A State D is the same as state A F: . . . we are here, same as state B State F is the same as State B G: Turn left until. . .

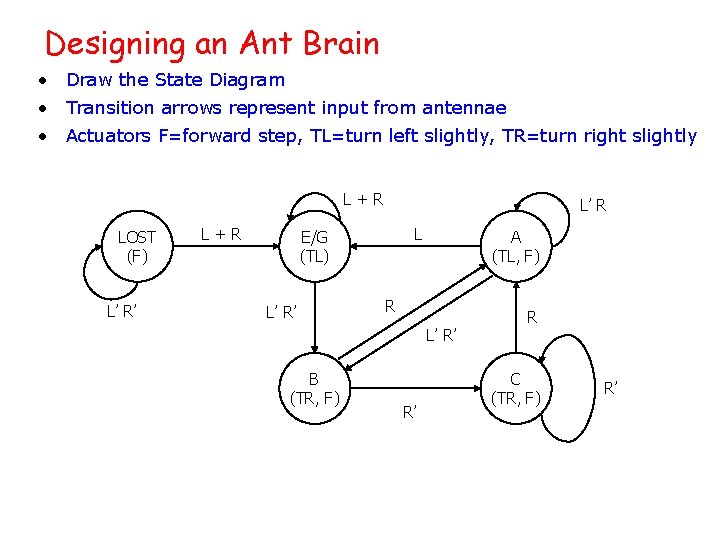
Designing an Ant Brain • Draw the State Diagram • Transition arrows represent input from antennae • Actuators F=forward step, TL=turn left slightly, TR=turn right slightly L+R LOST (F) L’ R’ L+R L’ R L E/G (TL) L’ R’ A (TL, F) R L’ R’ B (TR, F) R’ R C (TR, F) R’

Synthesizing the Ant Brain Circuit • Encode States Using a Set of State Variables • The encoding is an arbitrary choice - may affect cost, speed • Use Transition Truth Table • Define next state function for each state variable • Define output function for each output • Implement next state and output functions using combinational logic

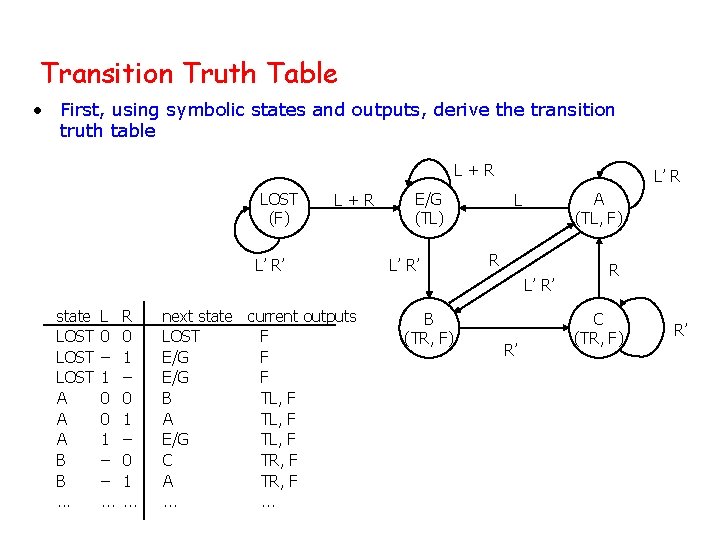
Transition Truth Table • First, using symbolic states and outputs, derive the transition truth table L+R LOST (F) L+R L’ R’ E/G (TL) L’ R’ L’ R A (TL, F) L R L’ R’ state LOST A A A B B. . . L 0 – 1 0 0 1 – –. . . R 0 1 – 0 1. . . next state current outputs LOST F E/G F B TL, F A TL, F E/G TL, F C TR, F A TR, F. . . B (TR, F) R’ R C (TR, F) R’

• Synthesis 5 states : at least 3 state variables required (X, Y, Z) • State assignment: • Convert symbolic states to bits (in this case, arbitrarily chosen) • Also represent outputs with bits it now remains state L R next state outputs to "synthesize" X, Y, Z X', Y', Z' F TR TL these 6 functions: to design output logic 000 0 0 000 1 0 0 and next state logic to 000 0 1 001 1 0 0 produce this result. . . . 010 0 0 011 1 010 0 1 010 1 0 001 1 010 1 1 001 1 011 0 0 100 1 1 0 011 0 1 010 1 1 0. . . . LOST E/G A B C - 000 001 010 011 100 An alternative Assignment: LOST - 000 E/G - 101 A - 110 B - 111 C - 100

Synthesis of Next State and Output Functions solve (using K-maps) for each output and next state e. g. state X, Y, Z 000 000 001 001 010 010 011 100 inputs L R 0 0 - 1 1 0 0 0 1 1 - 0 - 1 next state X+, Y+, Z+ 000 001 011 010 001 100 010 outputs F TR TL 1 0 0 1 0 0 1 1 0 1 1 0 TR = X + Y Z X+ = X R’ + Y Z R’ = R’ TR 3 state bits + 2 inputs means 25 = 32 rows in the transition table. Here we only show those we care about. e. g. : Unused states 101, 110 & 111 are missing Assumed don't cares

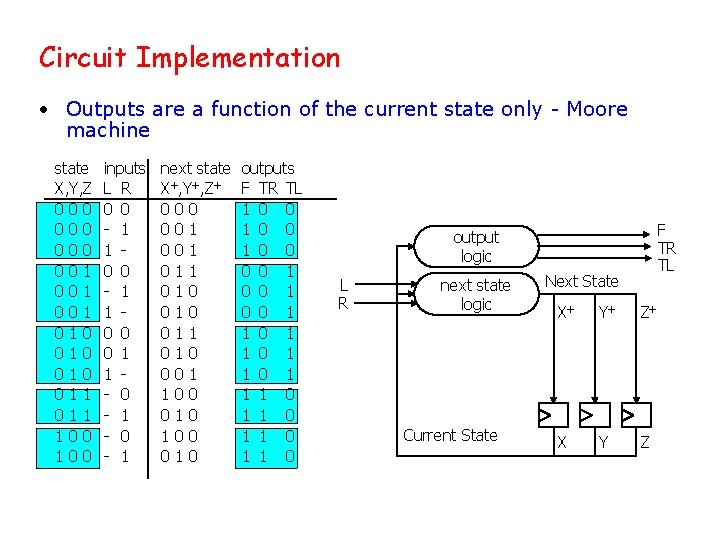
Circuit Implementation • Outputs are a function of the current state only - Moore machine state X, Y, Z 000 000 001 001 010 010 011 100 inputs L R 0 0 - 1 1 0 0 0 1 1 - 0 - 1 next state X+, Y+, Z+ 000 001 011 010 001 100 010 outputs F TR TL 1 0 0 1 0 0 1 1 0 1 1 0 F TR TL output logic L R next state logic Current State Next State X+ Y+ Z+ X Y Z

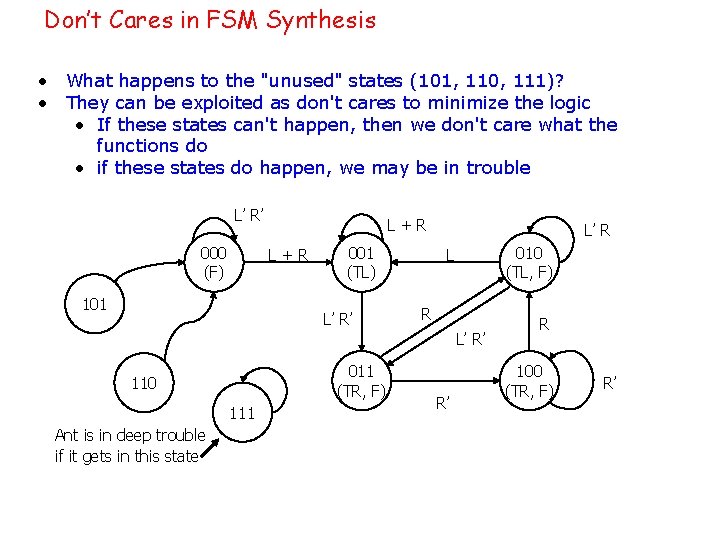
Don’t Cares in FSM Synthesis • What happens to the "unused" states (101, 110, 111)? • They can be exploited as don't cares to minimize the logic • If these states can't happen, then we don't care what the functions do • if these states do happen, we may be in trouble L’ R’ 000 (F) L+R 101 001 (TL) L’ R’ L’ R 010 (TL, F) L R L’ R’ 011 (TR, F) 110 111 Ant is in deep trouble if it gets in this state R’ R 100 (TR, F) R’

State Minimization • Fewer states may mean fewer state variables • High-level synthesis may generate many redundant states • Two states are equivalent if they are impossible to distinguish from the outputs of the FSM, i. e. , for any input sequence the outputs are the same • Two conditions for two states to be equivalent: 1) Output must be the same in both states (The nodes in the state diagram must be the same) 2) Must transition to equivalent states for all input combinations (The arrows FROM the nodes in the state diagram must result in the same state)