Anlisis de Varianza ANOVA Ing Ral Alvarez Guale

Análisis de Varianza (ANOVA) Ing. Raúl Alvarez Guale, MPC

Motivación • En sesiones anteriores se ha visto prueba de hipótesis referentes a dos medias poblacionales. • En base a muestras de dos poblaciones se trataba de testear si las medias poblacionales diferían: – Ho : u 1 = u 2 – HA : u 1 ≠ u 2 Para un nivel de significancia dado. 12 -2

Motivación • En esta sesión se enfoca el caso de testear a través de muestras, para un nivel de significancia dado, si las medias de tres o más poblaciones difieren: – Ho : – HA : u 1 = u 2 = u 3 =…. . = un Al menos de las medias poblacionales difieren. 12 -3

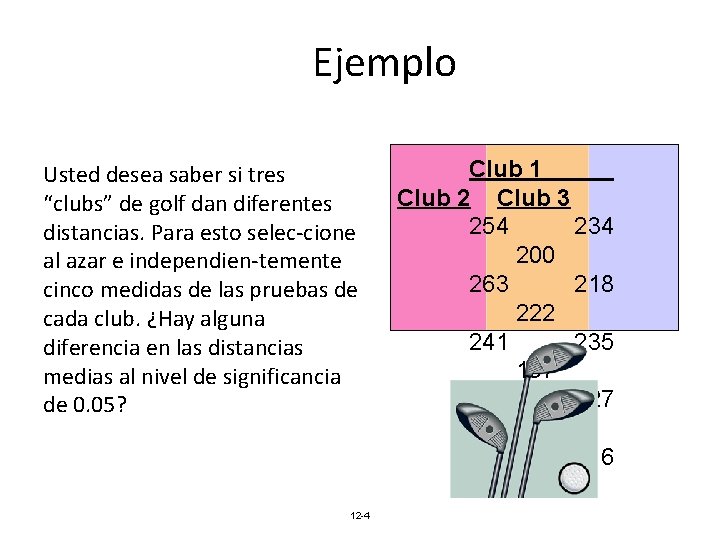
Ejemplo Usted desea saber si tres “clubs” de golf dan diferentes distancias. Para esto selec-cione al azar e independien-temente cinco medidas de las pruebas de cada club. ¿Hay alguna diferencia en las distancias medias al nivel de significancia de 0. 05? 12 -4 Club 1 Club 2 Club 3 254 234 200 263 218 222 241 235 197 237 227 206 251 216 204

Objetivos • Reconocer situaciones en las que se usa el análisis de varianza (ANOVA). • Entender diferentes diseños de análisis de varianza. • Desarrollar ANOVA de un factor (manualmente y con la ayuda de programas) e interpretar el resultado. • Ejecutar e interpretar procesos de comparación por pares (después del análisis de varianza). • Desarrollar ANOVA de Bloques Completamente Aleatorizados. • Desarrollar ANOVA de dos factores con réplicas a través de Excel o SPSS. 12 -5

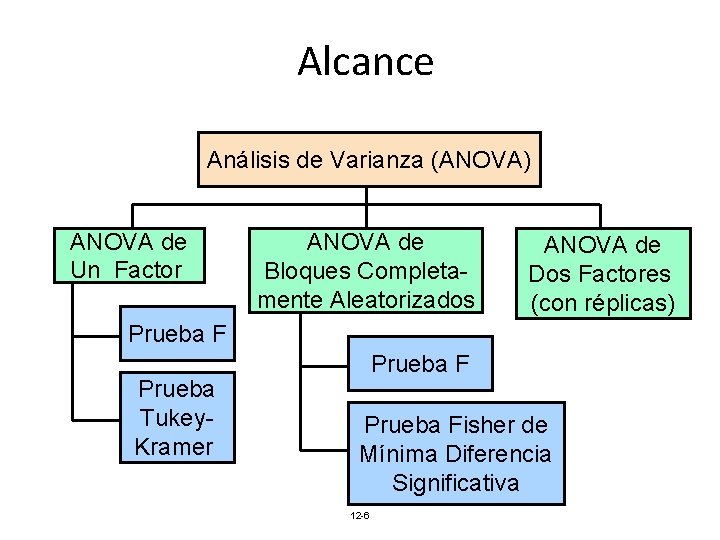
Alcance Análisis de Varianza (ANOVA) ANOVA de Un Factor ANOVA de Bloques Completamente Aleatorizados ANOVA de Dos Factores (con réplicas) Prueba F Prueba Tukey. Kramer Prueba Fisher de Mínima Diferencia Significativa 12 -6

Lógica del Análisis de Varianza • El investigador controla una o más variables independientes: – Llamadas factores. – Cada factor tiene dos o más niveles o tratamientos (o categorías/ clasificaciones). • Observar los efectos en la variable dependiente – Repuesta a niveles de la variable independiente. • Diseño experimental: Plan para probar hipótesis. 12 -7

Propósito del Análisis de Varianza • Supóngase que en un experimento agrícola cuatro tratamientos químicos diferentes del suelo producen rendimientos medios de trigo de 28, 22, 18 y 24 hl/ha respectivamente. ¿Hay una diferencia apreciable en estas medias o la dispersión observada simplemente se debe al azar?

Clasificación Simple o Experimentos de un Factor • En un experimento de un factor se obtienen medidas u observaciones para z grupos independientes de muestras, donde el número de medidas en cada grupo es b. • Hablamos de a tratamientos cada uno de los cuales tiene b repeticiones o réplicas.

Clasificación Simple o Experimentos de un Factor-Iguales número de Observaciones

Diseño Completamente Aleatorizado (Un Factor) • Las unidades experimentales (sujetos) son asignados al azar a los niveles del factor. • Sólo hay un factor (variable independiente) – Con dos o más niveles o tratamientos • Analizado por – Análisis de varianza de un factor (one-way ANOVA). • Llamado Diseño Balanceado si todos los niveles del factor tienen igual tamaño de muestra. 12 -11

Análisis de Varianza de Un Factor • Evalúa la igualdad entre las medias de dos o más poblaciones Ejemplos: ● Tasas de accidentes para el 1 er, 2 do y 3 er turno ● Kilometrajes esperados por galón para 5 marcas de neumáticos • Supuestos – Las poblaciones tienen distribución normal – Las poblaciones tienen igual varianza – Las muestras son aleatorias e independientes – La medida de los datos es de intervalo o razón 12 -12

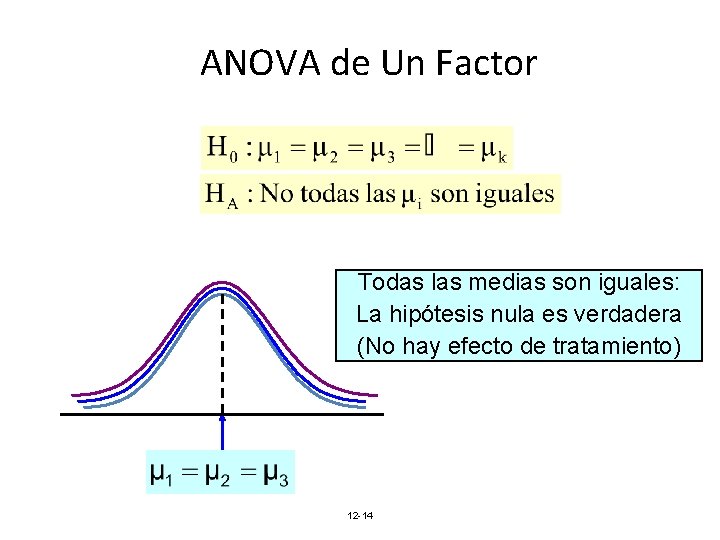
One-Way ANOVA: Hipótesis • – Todas las medias poblacionales son iguales – Es decir, no hay efecto de tratamiento (no hay variación entre las medias de los grupos) • – Al menos dos medias poblacionales son diferentes – Es decir, hay efecto de tratamiento – No significa que todas las medias poblacionales sean diferentes (algunos pares podrían ser iguales) 12 -13

ANOVA de Un Factor Todas las medias son iguales: La hipótesis nula es verdadera (No hay efecto de tratamiento) 12 -14

ANOVA de Un Factor (continuación) Al menos dos medias son diferentes: La hipótesis nula no es verdadera (Hay efecto de tratamiento) o 12 -15

ANOVA de Un Factor • Supuestos – Las poblaciones tienen distribución normal – Las poblaciones tienen igual varianza – Las muestras son aleatorias e independientes – La medida de los datos es de intervalo o razón • Supuesto Normalidad. pdf • Supuesto Varianzas. pdf 12 -16

ANOVA de Un Factor Supuestos: • Si las muestras son del mismo tamaño, los procedimientos ANOVA son robustos, esto es las pruebas no se ven mayormente afectadas si los supuestos de normalidad e igual varianza no se cumplen. • Si las muestras no son del mismo tamaño, los procedimientos ANOVA aún son relativamente robustos si el ratio entre la muestra de mayor tamaño y la de menor tamaño no excede 1. 5. 12 -17

Diseños ANOVA Desagregar la variación total de los datos en términos de: • Las variaciones explicadas por los tratamientos o niveles. • Las variaciones aleatorias al interior de cada tratamiento o nivel. 12 -18

Fórmulas •

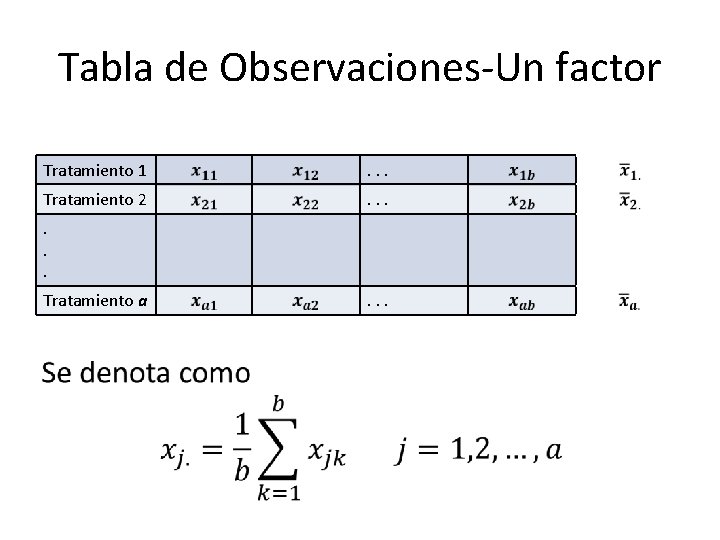
Tabla de Observaciones-Un factor Tratamiento 1 . . . Tratamiento 2 . . . Tratamiento a . . .

Desagregando la Variación Total • La variación total puede ser desagregada en dos partes: SST = SSB + SSW 12 -21

Variación Total •

Variación dentro de Tratamientos •

Variación entre Tratamientos •

• Variación Total = Variación dentro de tratamientos + Variación entre tratamientos

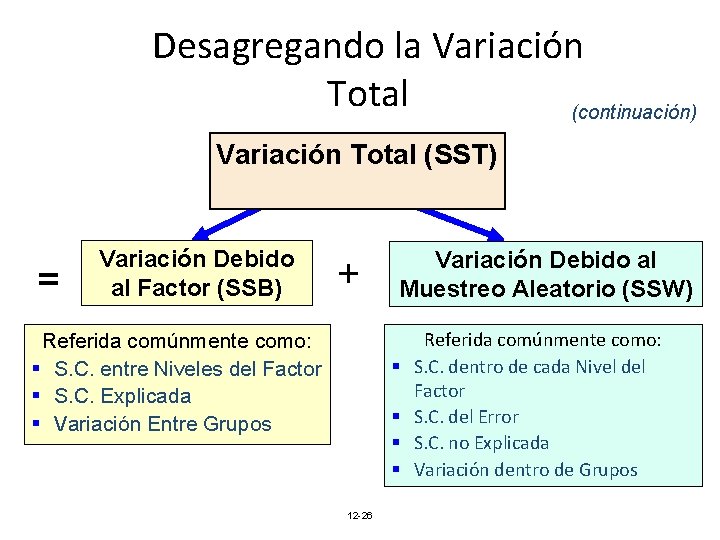
Desagregando la Variación Total (continuación) Variación Total (SST) = Variación Debido al Factor (SSB) + Referida comúnmente como: § S. C. entre Niveles del Factor § S. C. Explicada § Variación Entre Grupos Variación Debido al Muestreo Aleatorio (SSW) § § 12 -26 Referida comúnmente como: S. C. dentro de cada Nivel del Factor S. C. del Error S. C. no Explicada Variación dentro de Grupos

Desagregando la Variación Total (continuación) SST = SSB + SSW Variación Total (SST) = Dispersión total de los valores individuales. Variación entre niveles del factor (SSB) = Dispersión entre las medias muestrales del factor. Variación dentro de los niveles del factor (SSW) = Dispersión que existe entre los datos al interior de cada nivel del factor. 12 -27

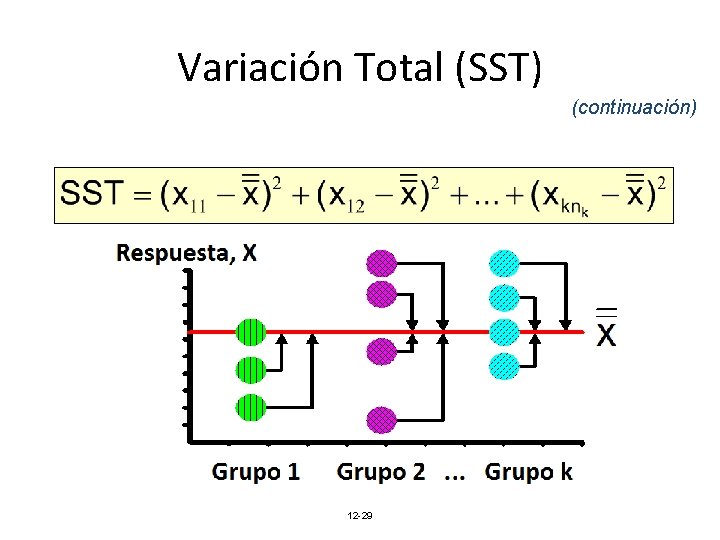
Variación Total (SST) SST = SSB + SSW Donde: SST = Suma total de cuadrados k = Número de poblaciones (niveles) ni = Tamaño muestral de la población i. xij = jma medida de la muestra correspondiente a la población i. x = Gran media (media de todos los datos) 12 -28

Variación Total (SST) (continuación) 12 -29

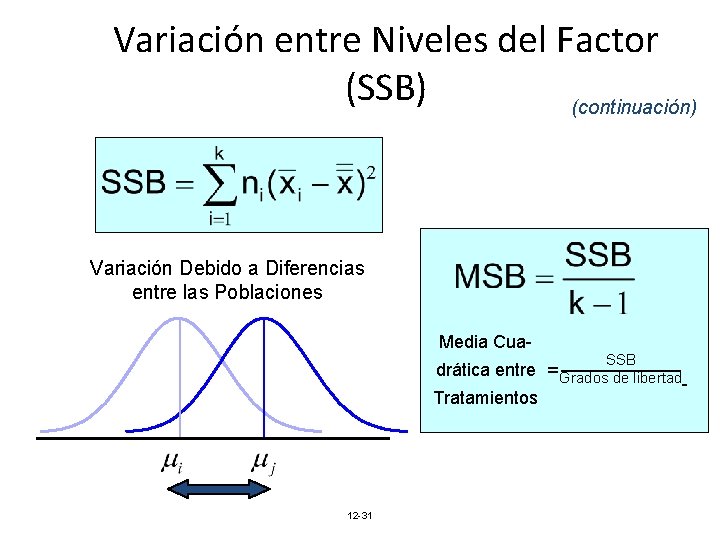
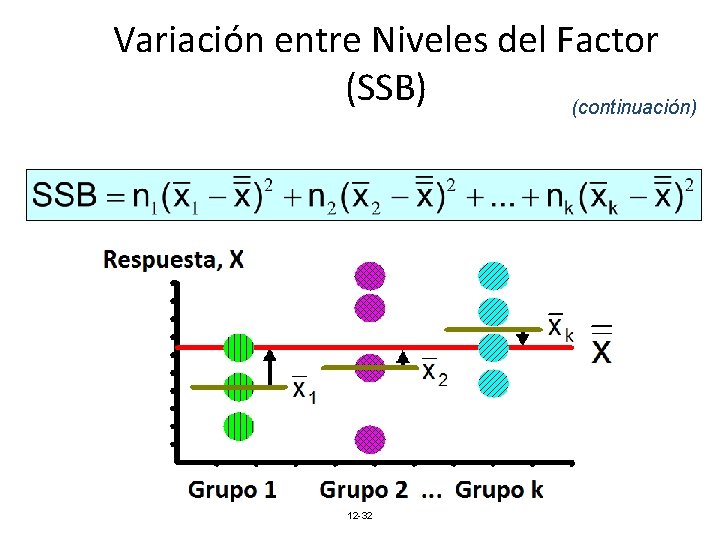
Variación entre Niveles del Factor (SSB) SST = SSB + SSW Donde: SSB = Suma de cuadrados entre tratamientos k = Número de poblaciones (niveles) ni = Tamaño muestral de la población i. xi = Media muestral de la población i. x = Gran media (media de todos los datos) 12 -30

Variación entre Niveles del Factor (SSB) (continuación) Variación Debido a Diferencias entre las Poblaciones Media Cua. SSB drática entre =Grados de libertad Tratamientos 12 -31

Variación entre Niveles del Factor (SSB) (continuación) 12 -32

Variación dentro de los Niveles del Factor (SSW) SST = SSB + SSW Donde: SSW = Suma de cuadrados del error k = Número de poblaciones ni = Tamaño de la muestra de la población i xi = Media muestral de la población i xij = jma medida de la muestra correspondiente a la población i. 12 -33

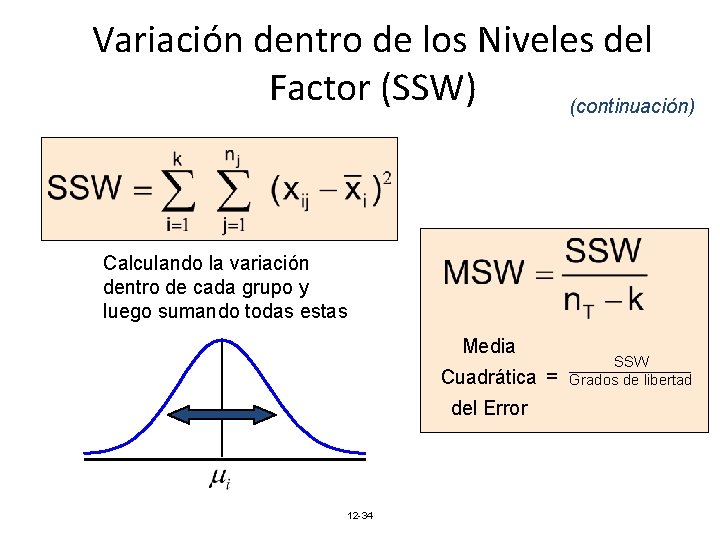
Variación dentro de los Niveles del Factor (SSW) (continuación) Calculando la variación dentro de cada grupo y luego sumando todas estas Media Cuadrática = del Error 12 -34 SSW Grados de libertad

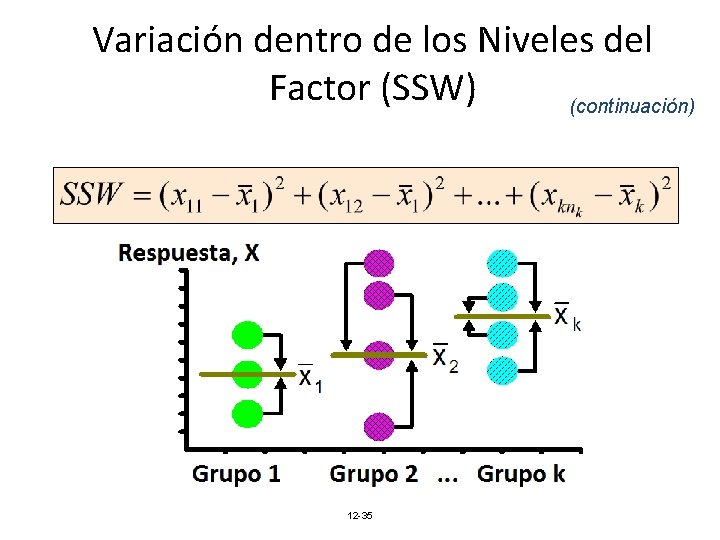
Variación dentro de los Niveles del Factor (SSW) (continuación) 12 -35

ANOVA de Un Factor: Estadístico de prueba F H 0: μ 1= μ 2 = … = μ k HA: Al menos dos medias poblacionales son diferentes • Estadístico de prueba: MSB: Media cuadrática entre tratamientos MSW: Media cuadrática dentro de tratamientos • Grados de libertad – glnumerador = k – 1 (k = Número de poblaciones) – gldenominador = n. T – k (n. T = Suma de todos los tamaños de muestra) 12 -36

ANOVA de Un Factor: Interpretación del estadístico F • El estadístico F es la razón de la media cuadrática entre tratamientos y la media cuadrátrica dentro de tratamientos – La razón siempre debe ser positiva – glnumerador = k -1, comúnmente será pequeño – gldenominador = n. T – k, comúnmente será grande La razón debería estar cerca a 1 si H 0: μ 1= μ 2 = … = μk es verdadera La razón debería ser más grande que 1 si H 0: μ 1= μ 2 = … = μk es falsa 12 -37

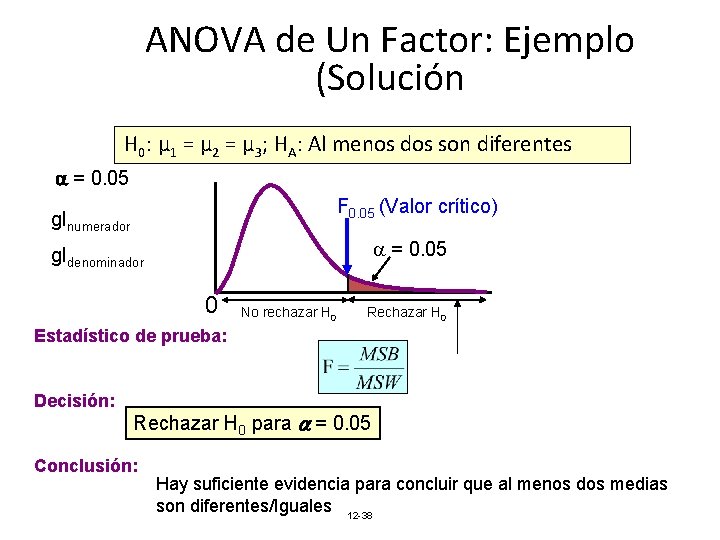
ANOVA de Un Factor: Ejemplo (Solución H 0: μ 1 = μ 2 = μ 3; HA: Al menos dos son diferentes = 0. 05 F 0. 05 (Valor crítico) glnumerador = 0. 05 gldenominador 0 No rechazar H 0 Rechazar H 0 Estadístico de prueba: Decisión: Rechazar H 0 para = 0. 05 Conclusión: Hay suficiente evidencia para concluir que al menos dos medias son diferentes/Iguales 12 -38

ANOVA: Pasos 1. 2. 3. 4. 5. 6. 7. 8. Especificar el parámetro de interés. Formular hipótesis. Fijar el nivel de significancia, . Seleccionar muestras aleatorias e independientes • Calcular las medias muestrales y la gran media. Determinar la regla de decisión. Verificar los supuestos: Normalidad e igualdad de varianzas. Crear la tabla ANOVA. Tomar una decisión e interpretar resultados. 12 -39

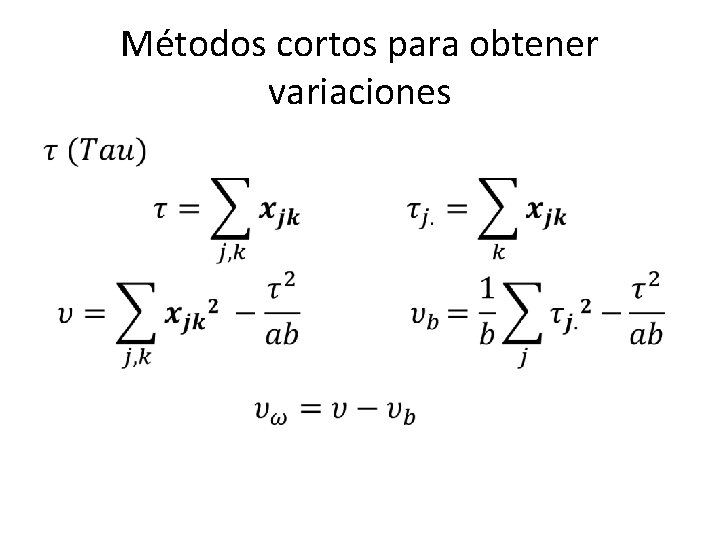
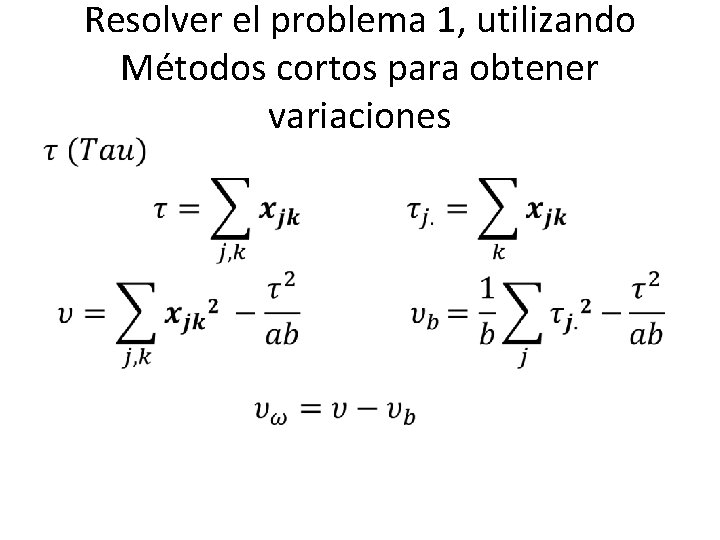
Métodos cortos para obtener variaciones •

Fórmulas cortas Tratamiento 1 . . . Tratamiento 2 . . . Tratamiento a . . .

Tablas de Análisis de varianza Variación Grados de Libertad a-1 a(b-1) ab-1 Media de Cuadrados F

Problema 1 • La tabla siguiente muestra los rendimientos en hl/ha de una cierta variedad de trigo cultivado en un tipo particular de suelo tratado con Químicos A, B o C. Hallar a) El rendimiento medio para los diferentes tratamientos, b) La gran media para todos los tratamientos, c) la variación total, d) la variación entre tratamientos, e) la variación dentro de tratamientos.

Problema 1 •

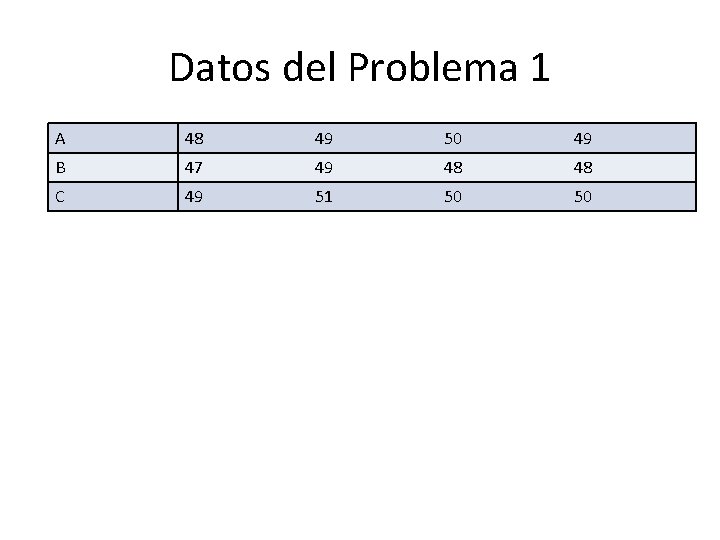
Datos del Problema 1 A 48 49 50 49 B 47 49 48 48 C 49 51 50 50

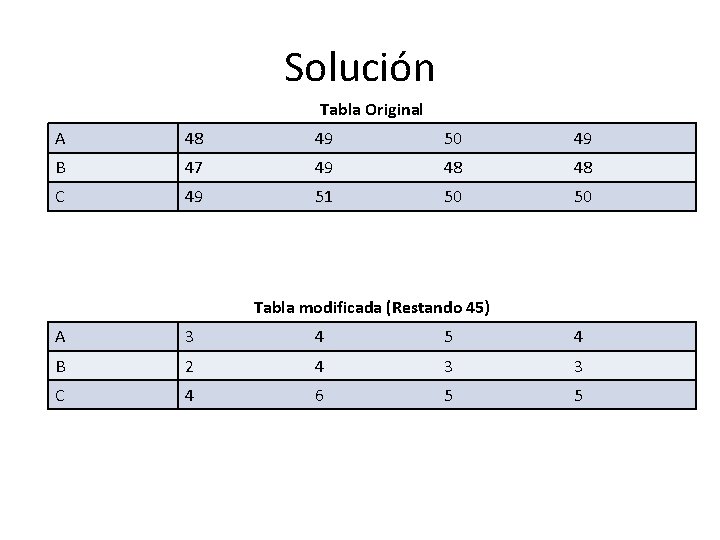
Solución Tabla Original A 48 49 50 49 B 47 49 48 48 C 49 51 50 50 Tabla modificada (Restando 45) A 3 4 5 4 B 2 4 3 3 C 4 6 5 5

a) Media de tratamientos Tabla modificada (Restando 45) A 3 4 5 5 4 B 2 4 3 3 3 C 4 6 5 5 5 • Por lo tanto son 49, 48 y 50 hl/ha para A, B y C (sumando 45 a cada resultado)

b) La gran media • Así la gran media para el conjunto original de datos es 45+4 = 49 hl/ha

c) Variación Total

d) Variación entre tratamientos •

e) Variación dentro de tratamientos

f)Y g) Estima insesgada de la varianza entre/dentro tratamiento •

h) Prueba de hipótesis 0. 05 •

i) Prueba de hipótesis 0. 01 •

Resumen del Problema 1 Variación Grados de Libertad a-1=2 a(b-1)=(3)(3)=9 ab-1=(3)(4)-1=11 Media de Cuadrados F

• Resolver el problema 1, utilizando Métodos cortos para obtener variaciones

c) Variación Total •

Variación entre y dentro de tratamiento •

Resumen Problema 2 A B C 3 2 4 4 4 6 5 3 5 4 3 5 16 12 20 256 144 400

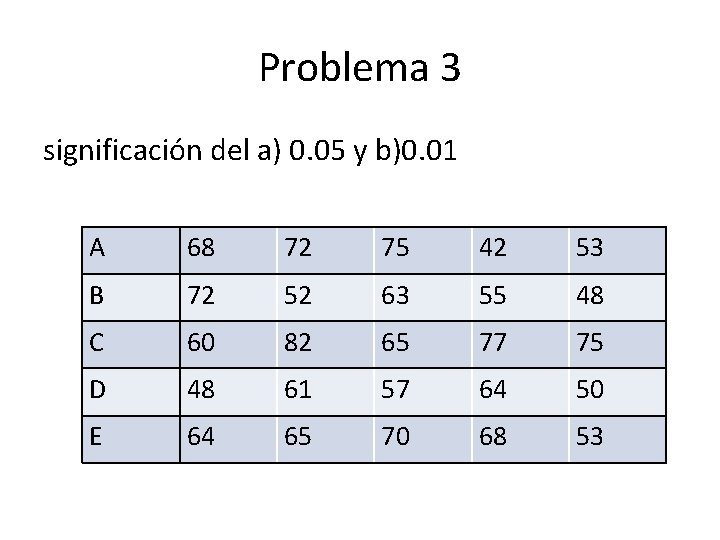
Problema 3 • Una compañía desea comprar una de cinco máquinas diferentes A, B, C, D, E. En un experimento diseñado para decidir si hay diferencia en el rendimiento de las máquinas, cinco operadores experimentados trabajan con las máquinas durante intervalos iguales. La siguiente tabla muestra el número de unidades producidas. Ensayar la hipótesis de

Problema 3 significación del a) 0. 05 y b)0. 01 A 68 72 75 42 53 B 72 52 63 55 48 C 60 82 65 77 75 D 48 61 57 64 50 E 64 65 70 68 53

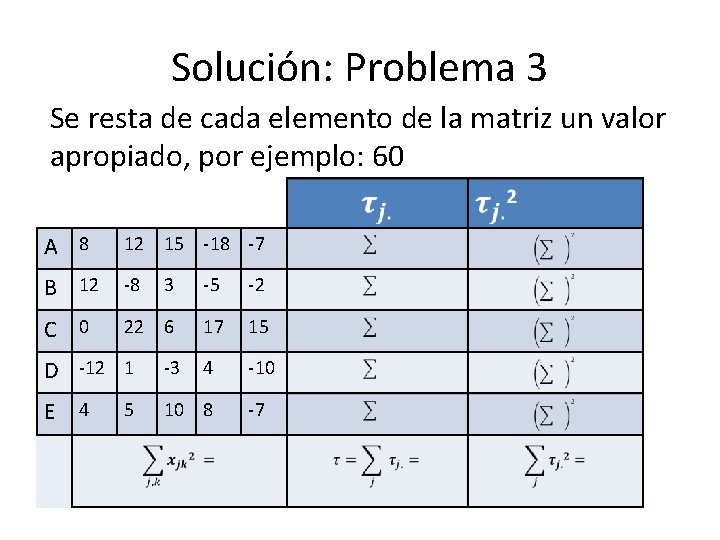
Solución: Problema 3 Se resta de cada elemento de la matriz un valor apropiado, por ejemplo: 60 A 8 12 15 -18 -7 B 12 -8 3 -5 -2 C 0 22 6 17 15 4 -10 D -12 1 -3 E 4 10 8 5 -7

Cálculos del Problema 3 A 8 12 15 -18 -7 10 100 B 12 -8 3 -5 -2 0 0 C 0 22 6 17 15 60 3600 4 -10 -20 400 -7 20 400 D -12 1 -3 E 4 10 8 5

Variaciones Totales • Se obtienen las variaciones totales, entre y dentro de cada tratamiento

Resumen del Problema 3 Variación Grados de Libertad a-1=4 a(b-1)=(5)(4)=20 ab-1=(5)(4)-1=24 Media de Cuadrados F

Conclusión: Problema 3 •

Clasificación Simple o Experimentos de un Factor-Diferentes número de Observaciones

Fórmulas •

Fórmulas cortas Tratamiento 1 . . . Tratamiento 2 . . . Tratamiento a . . .

Tabla de Análisis de Varianza Variación Grados de Libertad a-1 n-a n-1 Media de Cuadrados F

Problema 4 • La siguiente tabla muestra la duración en horas de las muestras de tres tipos diferentes de tubos de televisión fabricados por una compañía. Utilizando el método corto, ensayar al nivel de significación del (a)0. 05, (b) 0. 01 si hay diferencia en los tres tipos. Muestras Muestra 1 407 411 409 Muestra 2 404 406 408 405 Muestra 3 410 408 406 408 402

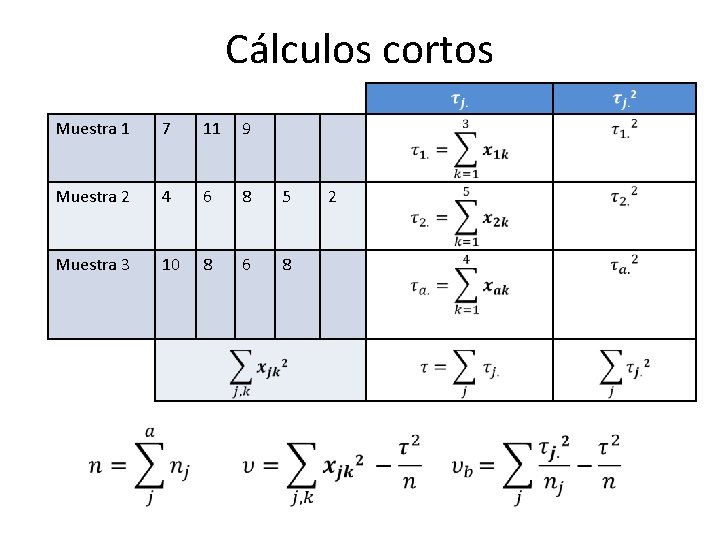
Cálculos cortos Muestra 1 7 11 9 Muestra 2 4 6 8 5 Muestra 3 10 8 6 8 2

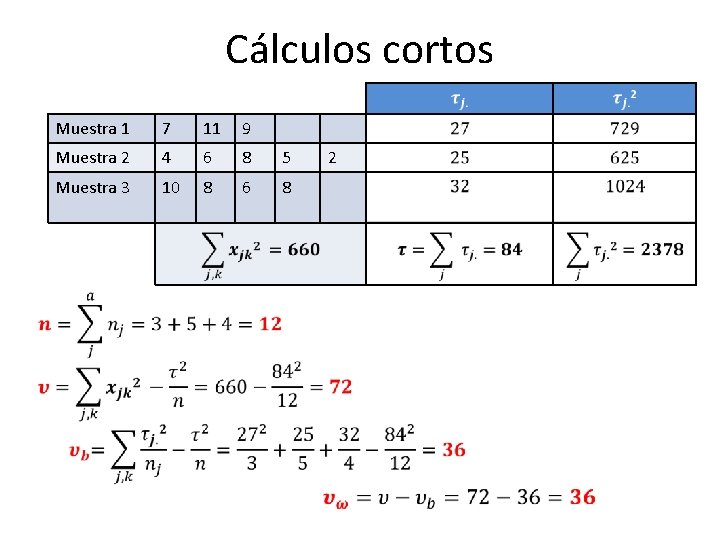
Cálculos cortos Muestra 1 7 11 9 Muestra 2 4 6 8 5 Muestra 3 10 8 6 8 2

Resumen del Problema 4 Variación Grados de Libertad a-1=3 -1=2 n-a=12 -3=9 Media de Cuadrados F

Clasificación Simple o Experimentos de dos Factores

¿Cuándo utilizar? • Las ideas de análisis de varianza para clasificación simple o experimentos de un factor pueden generalizarse. Para la clasificación doble o experimentos de dos factores se ilustra por medio del siguiente ejemplo:

Ejemplo • Supóngase que en un experimento agrícola consiste en examinar los rendimientos por acre de 4 variedades diferentes de trigo (tratamiento), donde cada variedad se cultiva en 5 parcelas diferentes (bloques). En este caso hay dos clasificaciones o factores, puesto que puede existir diferencias en rendimiento por tratamiento o bloques

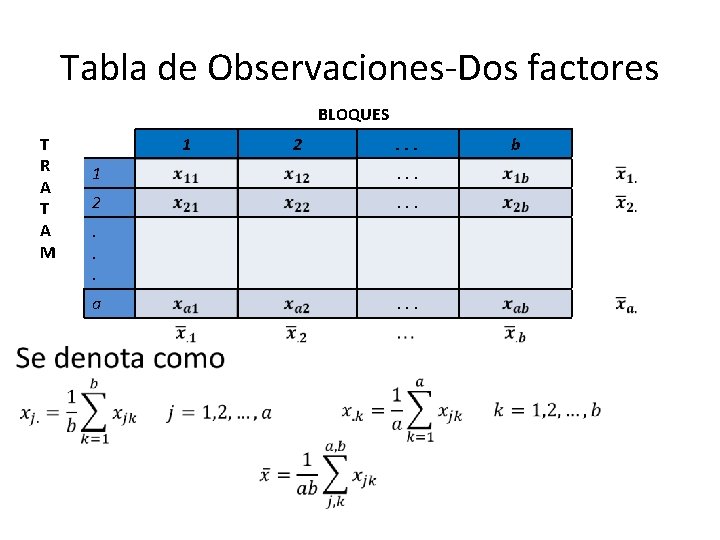
Tabla de Observaciones-Dos factores BLOQUES T R A T A M 1 2 . . . 1 . . . 2 . . . a . . . b

Fórmulas cortas T R A T A M I E N T O S 1 2 b . . . 1 . . . 2 . . . . a . .

Donde •

Tabla de Análisis de Varianza Variación Grados de Libertad a-1 b-1 (a-1)(b-1) ab-1 Media de Cuadrados F

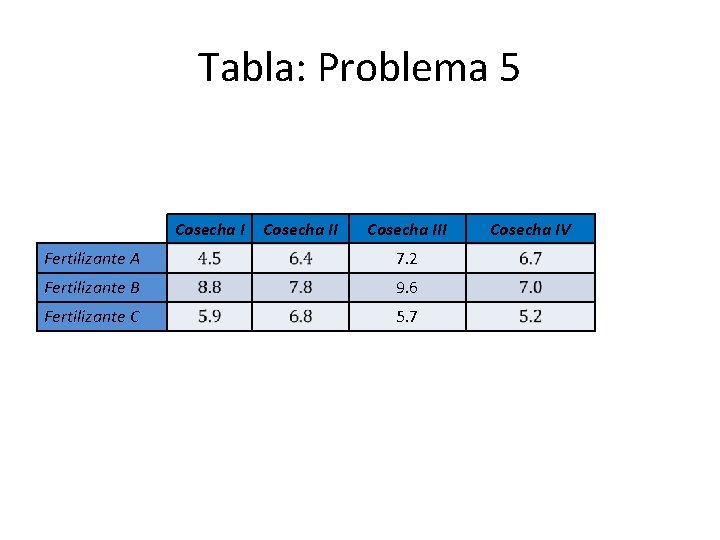
Problema 5 La siguiente tabla muestra los rendimientos por acre de cuatro cosechas de plantas diferentes cultivadas en parcelas tratadas con tres tipos diferentes de fertilizantes. Utilizando el método corto, ensayar el nivel de significación de 0, 01 si (a) hay una diferencia significativa en rendimiento por acre debida a los fertilizantes, (b) hay una diferencia significativa en rendimiento por acre debido a las cosechas.

Tabla: Problema 5 Cosecha III Fertilizante A 7. 2 Fertilizante B 9. 6 Fertilizante C 5. 7 Cosecha IV

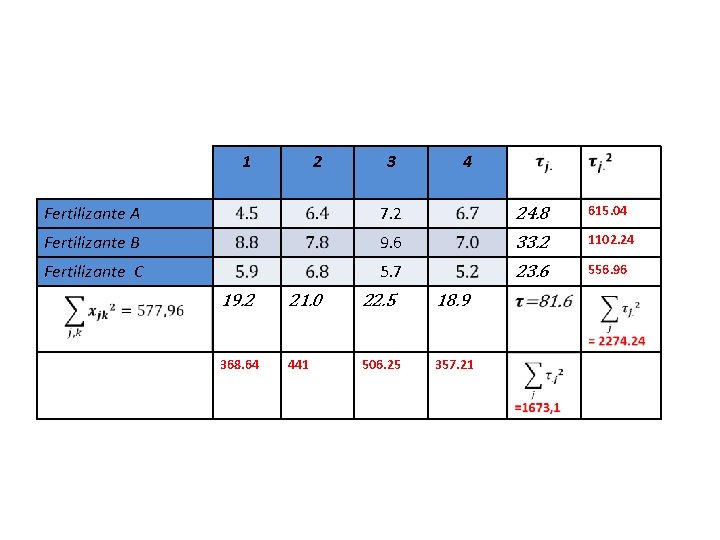
1 2 3 4 Fertilizante A 7. 2 24. 8 615. 04 Fertilizante B 9. 6 33. 2 1102. 24 Fertilizante C 5. 7 23. 6 556. 96 19. 2 21. 0 22. 5 18. 9 368. 64 441 506. 25 357. 21

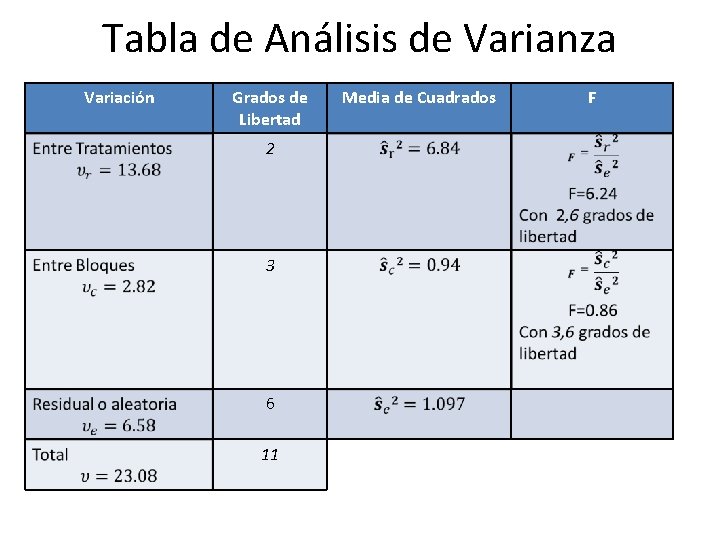
Tabla de Análisis de Varianza Variación Grados de Libertad 2 3 6 11 Media de Cuadrados F

Conclusiones: Problema 5 • Al nivel de significación de 0. 05 con 2, 6 grados de libertad, F 0. 95 = 5. 14, entonces, ya que 6. 24>5. 14 podemos rechazar la hipótesis de que las medias de fila son iguales y concluir que al nivel de 0. 05 hay una diferencia significativa en el rendimiento debido a los fertilizantes.

Conclusiones: Problema 5 • Ya que el valor de F correspondiente a las diferencias en las medias de columna es menor que 1 podemos concluir que no hay diferencia significativa en el rendimiento debido a las cosechas.