Anlise da Estabilidade de Sistemas Dinmicos Aula Terica

Análise da Estabilidade de Sistemas Dinâmicos Aula Teórica – Semana 9 PC - Prof. RCBetini 1

Análise da Estabilidade • O principal requisito de um sistema de controle é garantir a estabilidade em qualquer condição de operação do sistema. • Garantindo-se a estabilidade procura-se atender aos outros requisitos de regime permanente e regime transitório. • Considera-se que um sistema é estável quando ao ser aplicado um sinal finito a sua entrada, após um período transitório obtém-se um sinal finito na saída. • Se a saída tender a um valor infinito ou não estabilizar em um valor finito constante, o sistema é considerado instável. PC - Prof. RCBetini 2

Análise da Estabilidade • Pólos localizados no SPE do Plano s (parte real negativa do pólo), resulta em exponenciais decrescentes com o tempo, caracterizando o sistema estável. • Por outro lado, pólos no SPD (parte real positiva do pólo), resulta em exponenciais crescentes com o tempo o que caracteriza um sistema como instável. • Portanto, para que um sistema seja estável basta que as raízes do denominador da Função de Transferência em Malha Fechada apresentem parte real negativa. • Para sistemas de 1ª e 2ª ordem pode-se verificar com facilidade a Estabilidade. • Entretanto sistemas de ordem superior torna-se mais difícil verificar a Estabilidade. • Também pode ser necessário verificar a influência da variação de algum parâmetro do sistema, na sua Estabilidade. • Para estes casos pode-se adotar o critério de ROUTHHURWITZ. PC - Prof. RCBetini 3

Análise da Estabilidade – Método de ROUTH-HURWITZ PC - Prof. RCBetini 4

Análise da Estabilidade – Método de ROUTH-HURWITZ PC - Prof. RCBetini 5

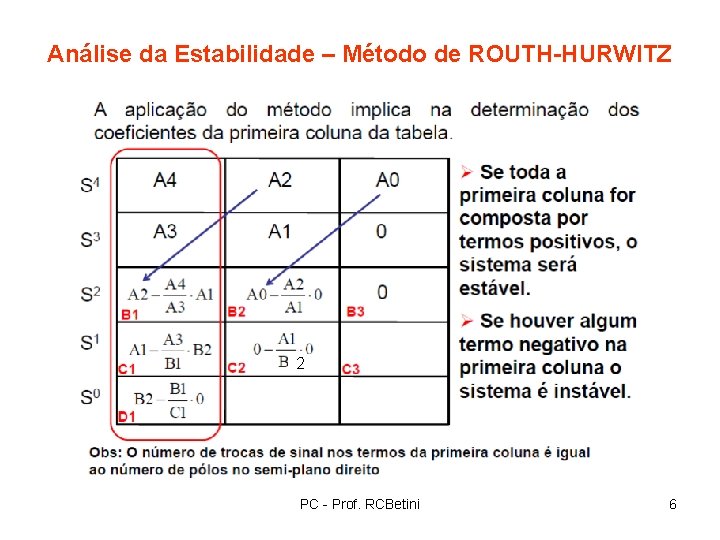
Análise da Estabilidade – Método de ROUTH-HURWITZ 2 PC - Prof. RCBetini 6

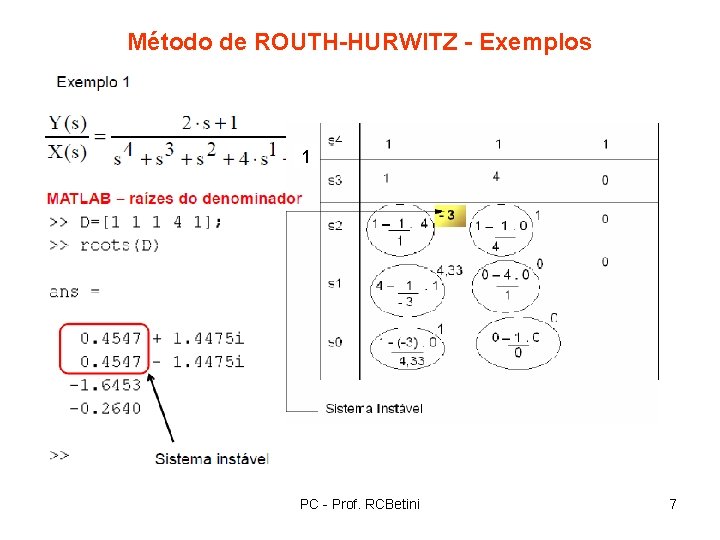
Método de ROUTH-HURWITZ - Exemplos 1 PC - Prof. RCBetini 7

Método de ROUTH-HURWITZ - Exemplos (D) PC - Prof. RCBetini 8

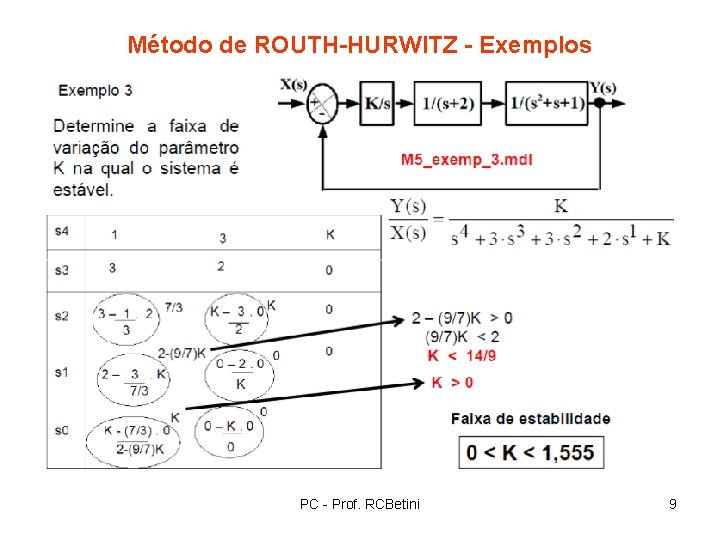
Método de ROUTH-HURWITZ - Exemplos PC - Prof. RCBetini 9

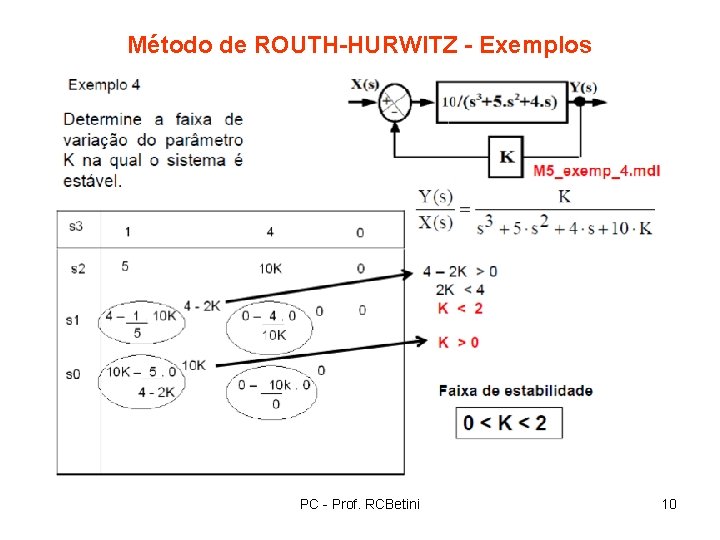
Método de ROUTH-HURWITZ - Exemplos PC - Prof. RCBetini 10