Anisotropic Flow Sergei A Voloshin Wayne State University

Anisotropic Flow Sergei A. Voloshin Wayne State University, Detroit, Michigan Disclaimer: It must be something! - Not a real review – this is an introduction - Fully to Anisotropic Flow: Artistic! terminology, physics, - Art’s playground analysis techniques, achievements and problems, current status of the art. for many years - Many of the most recent results will be - Fun for everyone! discussed in the original talks at this School. - Apologies for not mentioning many good papers on the subject. This talk is based mostly on works where I participated and know the best. page 1 School of Collective Dynamics in High Energy Collisions, LBNL, May 19 -27, 2005 S. A. Voloshin

Outline Part I. Physics Part II. 1. Introduction. Definitions. 2. Directed flow - Physics of the “wiggle” - Blast wave parameterization - Coalescence I. Directed flow of light nuclei 3. Elliptic flow - General properties. “Early times” - Low Density and “Hydro” Limits - Phase transition - Blast wave. “Mass splitting” - Coalescence II. Constituent quarks. Resonances. - Elliptic flow at high pt’s. 4. Anisotropies and asymmetries - Femtoscopy of anisotropic source - High pt, 2 -particle correlations - Global polarization, Parity violation… Methods and Results 1. Non-flow estimates - From the “resolution plot” - Azimuthal correlations in pp and AA 2. Multiparticle correlations - 4 -particle cumulants. Methods. - Non-flow and flow fluctuations - Mixed harmonics. 3 -particle correlations. - Distributions in q-vector - Detector effects 3. Main results - Reaching the hydro limit - Mass splitting - Constituent quark scaling - Elliptic flow at high pt - v 1 and higher harmonics - other 4. Conclusion 5. Can we measure it? - correlations induced by flow - “Non-flow”. Flow fluctuations page 2 School of Collective Dynamics in High Energy Collisions, LBNL, May 19 -27, 2005 S. A. Voloshin

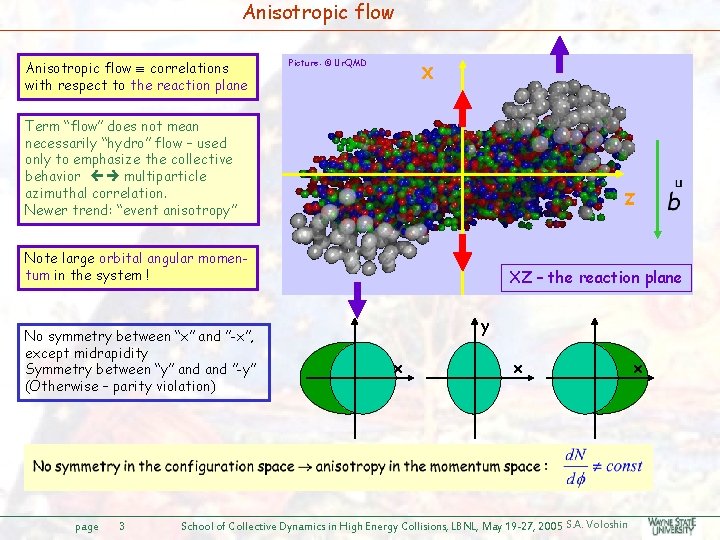
Anisotropic flow correlations with respect to the reaction plane Picture: © Ur. QMD X Term “flow” does not mean necessarily “hydro” flow – used only to emphasize the collective behavior multiparticle azimuthal correlation. Newer trend: “event anisotropy” Z Note large orbital angular momentum in the system ! No symmetry between “x” and ”-x”, except midrapidity Symmetry between “y” and ”-y” (Otherwise – parity violation) page 3 XZ – the reaction plane y x x School of Collective Dynamics in High Energy Collisions, LBNL, May 19 -27, 2005 S. A. Voloshin x

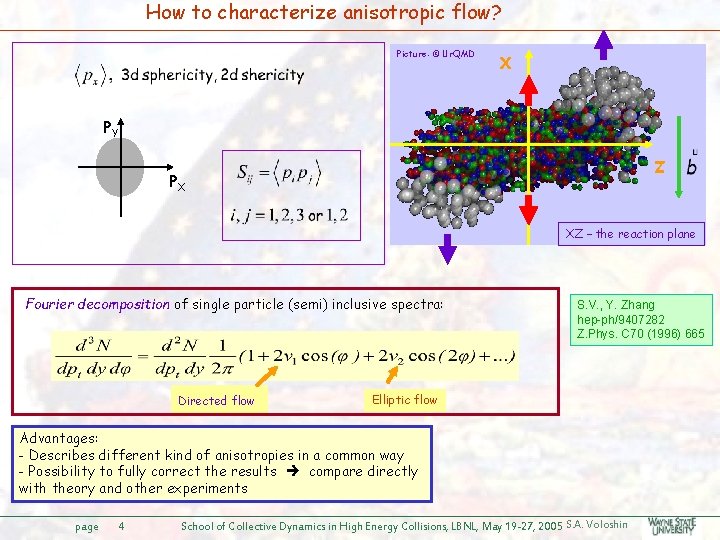
How to characterize anisotropic flow? Picture: © Ur. QMD X PY Z PX XZ – the reaction plane Fourier decomposition of single particle (semi) inclusive spectra: Directed flow S. V. , Y. Zhang hep-ph/9407282 Z. Phys. C 70 (1996) 665 Elliptic flow Advantages: - Describes different kind of anisotropies in a common way - Possibility to fully correct the results compare directly with theory and other experiments page 4 School of Collective Dynamics in High Energy Collisions, LBNL, May 19 -27, 2005 S. A. Voloshin

Definitions, continued Terminology: -harmonics, not multipoles (dipole, etc. required to describe 2 d or 3 d distributions) “… v 2 in pp collisions is almost 100% …” “… event anisotropy at high pt, elliptic flow at low pt…” Anisotropic flow correlations with respect to the reaction plane The situation with definitions is more complicated with two particle spectra measured with respect to the reaction plane. One way: parameterize, consider parameter dependence on pair orientation relative to the reaction plane. page 5 School of Collective Dynamics in High Energy Collisions, LBNL, May 19 -27, 2005 S. A. Voloshin

Why are we interested in anisotropic flow? Short answer: to learn more about system properties, evolution dynamics, hadronization – Anisotropic flow – as a measure of interactions in the system. Example: Does hydrodynamic model works? 1992 paper of J. -Y. Ollitrault PRD 46 (1992) 229 Collide Au+Au, is it enough to create QGP? • Is the system dense enough? What are the Quark & Gluon densities? • Does the system equilibrate? • What is the initial Temperature? To answer these questions we need to study the system early in the collision - hard (rare) probes: J/Psi, jets, dileptons, … - anisotropic flow ! Before discussing how the anisotropic flow let us set some time scales (in the center of mass frame): Passing time – the time two nuclei pass each other ~ RA/γ Initial transverse size of the system ~ RA Freeze-out time (could be up to a several RA) Directed flow is predefined at passing time, as at this moment the initial geometry of the system being set. Elliptic flow is mostly defined at the time scale of the initial size of the system for two reasons: -This is the time required for a fast particle to traverse the system -The time after which the spatial anisotropy diminish page 6 School of Collective Dynamics in High Energy Collisions, LBNL, May 19 -27, 2005 S. A. Voloshin

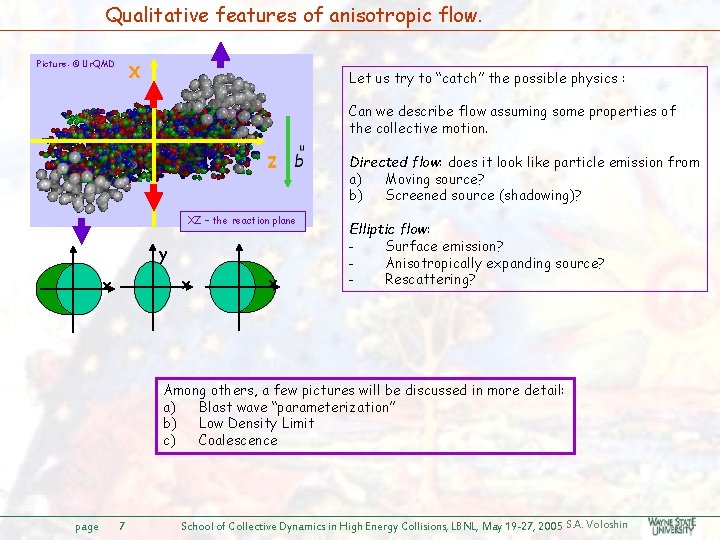
Qualitative features of anisotropic flow. Picture: © Ur. QMD X Let us try to “catch” the possible physics : Can we describe flow assuming some properties of the collective motion. Z XZ – the reaction plane y x x x Directed flow: does it look like particle emission from a) Moving source? b) Screened source (shadowing)? Elliptic flow: Surface emission? Anisotropically expanding source? Rescattering? Among others, a few pictures will be discussed in more detail: a) Blast wave “parameterization” b) Low Density Limit c) Coalescence page 7 School of Collective Dynamics in High Energy Collisions, LBNL, May 19 -27, 2005 S. A. Voloshin

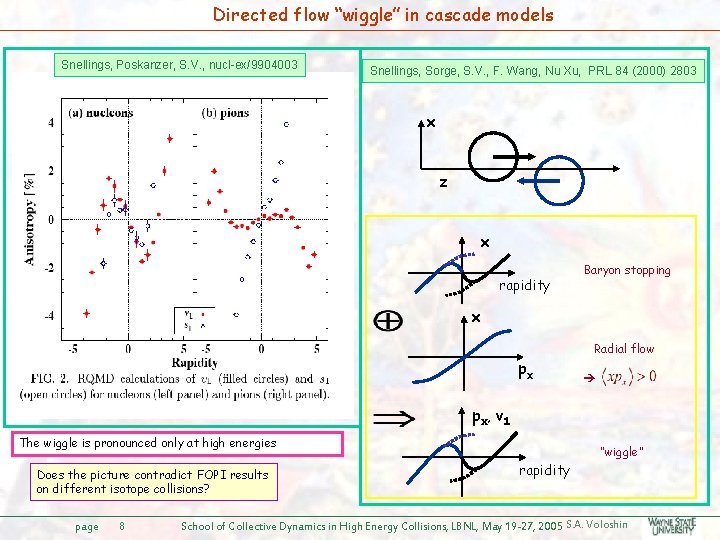
Directed flow “wiggle” in cascade models Snellings, Poskanzer, S. V. , nucl-ex/9904003 Snellings, Sorge, S. V. , F. Wang, Nu Xu, PRL 84 (2000) 2803 x z x rapidity Baryon stopping x Radial flow px px , v 1 The wiggle is pronounced only at high energies Does the picture contradict FOPI results on different isotope collisions? page 8 “wiggle” rapidity School of Collective Dynamics in High Energy Collisions, LBNL, May 19 -27, 2005 S. A. Voloshin

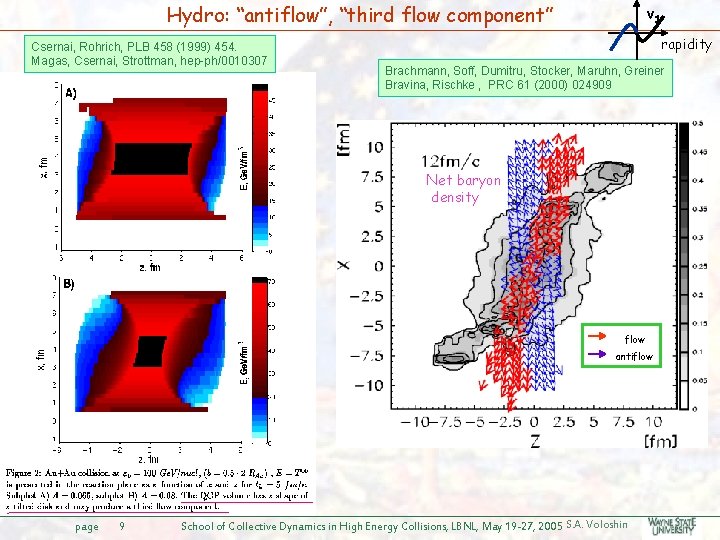
Hydro: “antiflow”, “third flow component” Csernai, Rohrich, PLB 458 (1999) 454. Magas, Csernai, Strottman, hep-ph/0010307 v 1 rapidity Brachmann, Soff, Dumitru, Stocker, Maruhn, Greiner Bravina, Rischke , PRC 61 (2000) 024909 Net baryon density flow antiflow page 9 School of Collective Dynamics in High Energy Collisions, LBNL, May 19 -27, 2005 S. A. Voloshin

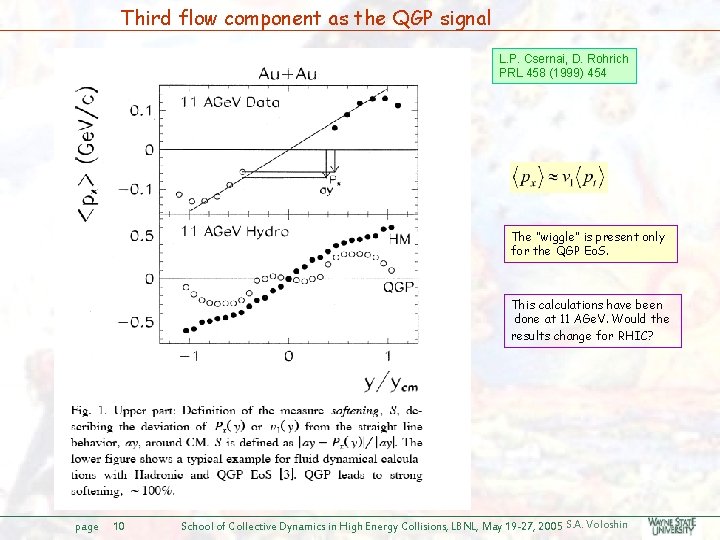
Third flow component as the QGP signal L. P. Csernai, D. Rohrich PRL 458 (1999) 454 The “wiggle” is present only for the QGP Eo. S. This calculations have been done at 11 AGe. V. Would the results change for RHIC? page 10 School of Collective Dynamics in High Energy Collisions, LBNL, May 19 -27, 2005 S. A. Voloshin

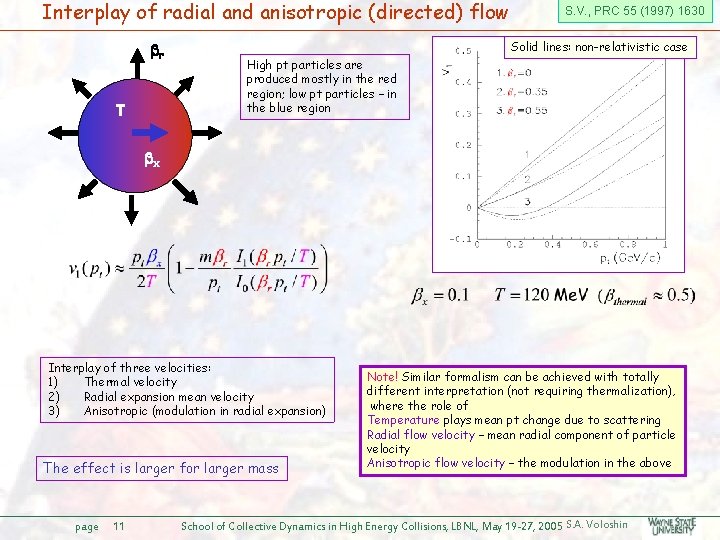
Interplay of radial and anisotropic (directed) flow r T S. V. , PRC 55 (1997) 1630 Solid lines: non-relativistic case High pt particles are produced mostly in the red region; low pt particles – in the blue region x Interplay of three velocities: 1) Thermal velocity 2) Radial expansion mean velocity 3) Anisotropic (modulation in radial expansion) The effect is larger for larger mass page 11 Note! Similar formalism can be achieved with totally different interpretation (not requiring thermalization), where the role of Temperature plays mean pt change due to scattering Radial flow velocity – mean radial component of particle velocity Anisotropic flow velocity – the modulation in the above School of Collective Dynamics in High Energy Collisions, LBNL, May 19 -27, 2005 S. A. Voloshin

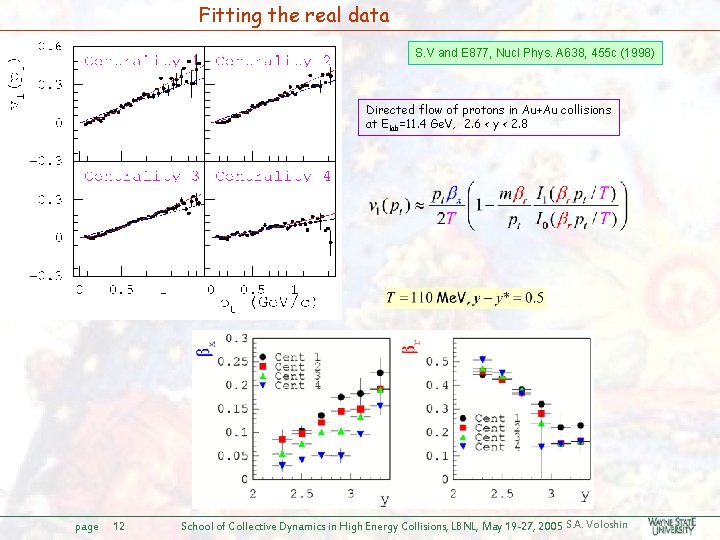
Fitting the real data S. V and E 877, Nucl Phys. A 638, 455 c (1998) Directed flow of protons in Au+Au collisions at Elab=11. 4 Ge. V, 2. 6 < y < 2. 8 page 12 School of Collective Dynamics in High Energy Collisions, LBNL, May 19 -27, 2005 S. A. Voloshin

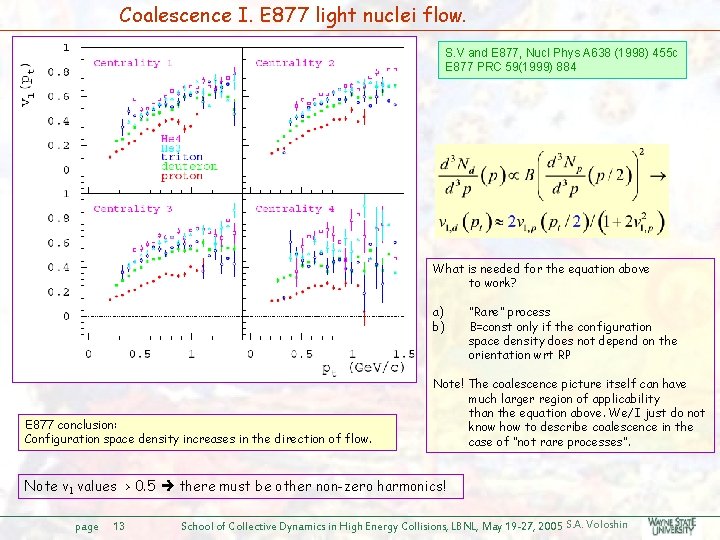
Coalescence I. E 877 light nuclei flow. S. V and E 877, Nucl Phys A 638 (1998) 455 c E 877 PRC 59(1999) 884 What is needed for the equation above to work? a) b) E 877 conclusion: Configuration space density increases in the direction of flow. “Rare” process B=const only if the configuration space density does not depend on the orientation wrt RP Note! The coalescence picture itself can have much larger region of applicability than the equation above. We/I just do not know how to describe coalescence in the case of “not rare processes”. Note v 1 values > 0. 5 there must be other non-zero harmonics! page 13 School of Collective Dynamics in High Energy Collisions, LBNL, May 19 -27, 2005 S. A. Voloshin

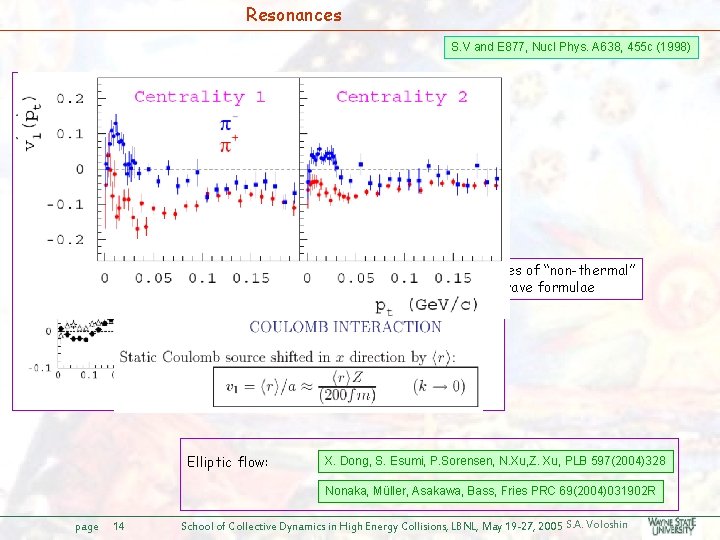
Resonances S. V and E 877, Nucl Phys. A 638, 455 c (1998) Note: one of the examples of “non-thermal” interpretation of blast wave formulae Elliptic flow: X. Dong, S. Esumi, P. Sorensen, N. Xu, Z. Xu, PLB 597(2004)328 Nonaka, Müller, Asakawa, Bass, Fries PRC 69(2004)031902 R page 14 School of Collective Dynamics in High Energy Collisions, LBNL, May 19 -27, 2005 S. A. Voloshin

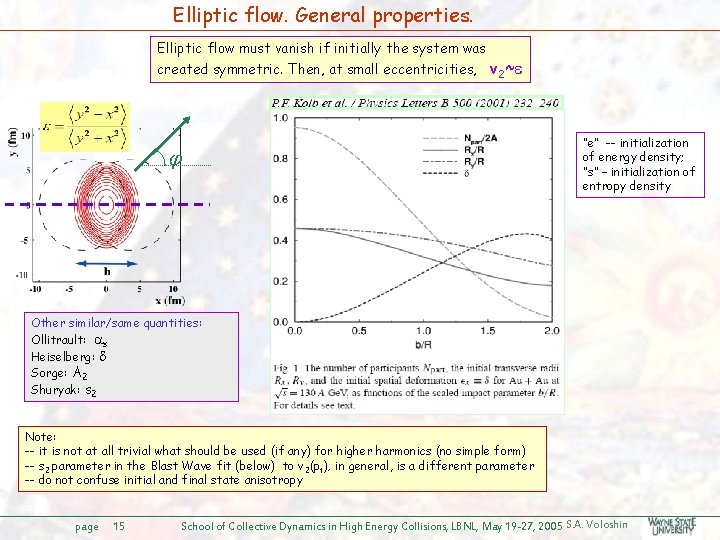
Elliptic flow. General properties. Elliptic flow must vanish if initially the system was created symmetric. Then, at small eccentricities, v 2~ “e” -- initialization of energy density; “s” – initialization of entropy density Other similar/same quantities: Ollitrault: s Heiselberg: Sorge: A 2 Shuryak: s 2 Note: -- it is not at all trivial what should be used (if any) for higher harmonics (no simple form) -- s 2 parameter in the Blast Wave fit (below) to v 2(pt), in general, is a different parameter -- do not confuse initial and final state anisotropy page 15 School of Collective Dynamics in High Energy Collisions, LBNL, May 19 -27, 2005 S. A. Voloshin

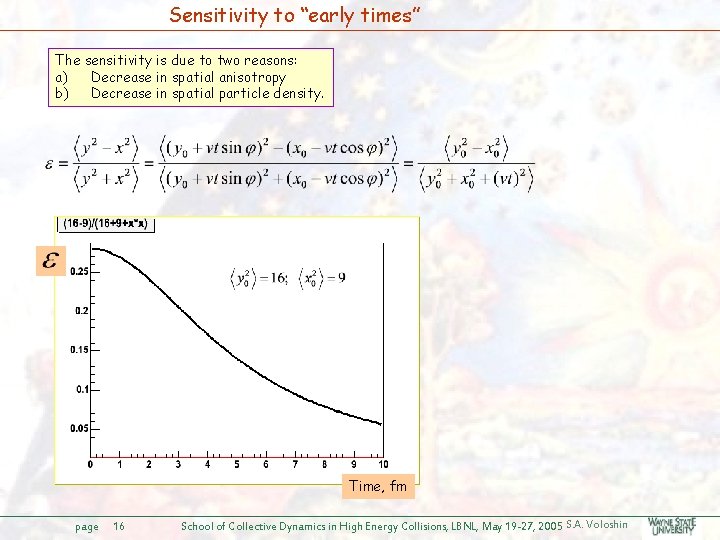
Sensitivity to “early times” The sensitivity is due to two reasons: a) Decrease in spatial anisotropy b) Decrease in spatial particle density. Time, fm page 16 School of Collective Dynamics in High Energy Collisions, LBNL, May 19 -27, 2005 S. A. Voloshin

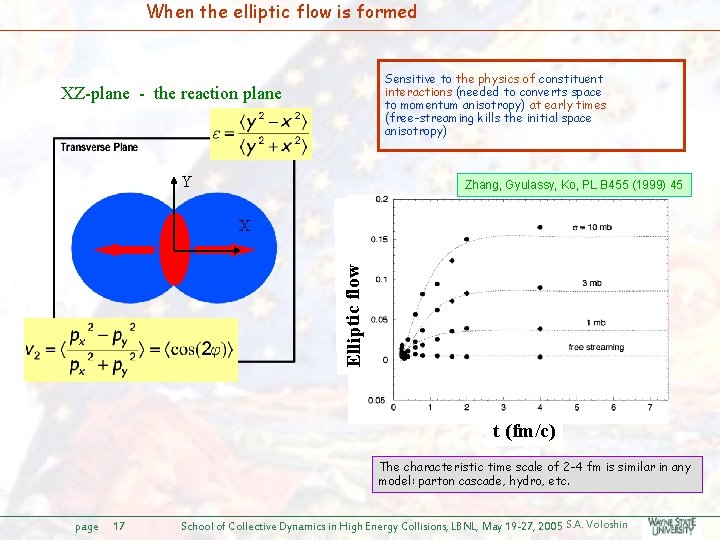
When the elliptic flow is formed Sensitive to the physics of constituent interactions (needed to converts space to momentum anisotropy) at early times (free-streaming kills the initial space anisotropy) XZ-plane - the reaction plane Y Zhang, Gyulassy, Ko, PL B 455 (1999) 45 Elliptic flow X t (fm/c) The characteristic time scale of 2 -4 fm is similar in any model: parton cascade, hydro, etc. page 17 School of Collective Dynamics in High Energy Collisions, LBNL, May 19 -27, 2005 S. A. Voloshin

Low density limit (called “collisionless” in the original paper of Heiselberg and Levy) Below - my own derivation of Heiselberg’s results Heiselberg & Levy, PRC 59 (1999) 2716 Change in the particle flux is proportional to the probability for the particle to interact. Integrations over: a) particle emission point b) Over the trajectory of the particle (time) with weight proportional to the density of other particles --“scattering centers” Particle density at time t assuming free streaming Note: (x-vt) changes very little over the entire history page 18 School of Collective Dynamics in High Energy Collisions, LBNL, May 19 -27, 2005 S. A. Voloshin

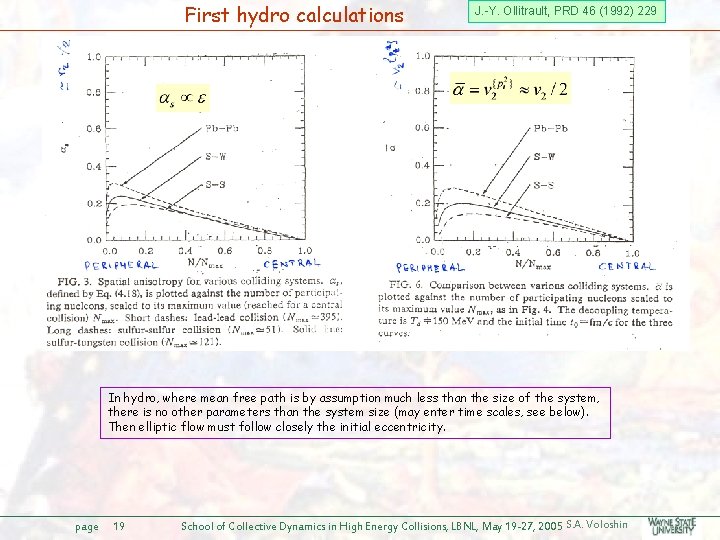
First hydro calculations J. -Y. Ollitrault, PRD 46 (1992) 229 In hydro, where mean free path is by assumption much less than the size of the system, there is no other parameters than the system size (may enter time scales, see below). Then elliptic flow must follow closely the initial eccentricity. page 19 School of Collective Dynamics in High Energy Collisions, LBNL, May 19 -27, 2005 S. A. Voloshin

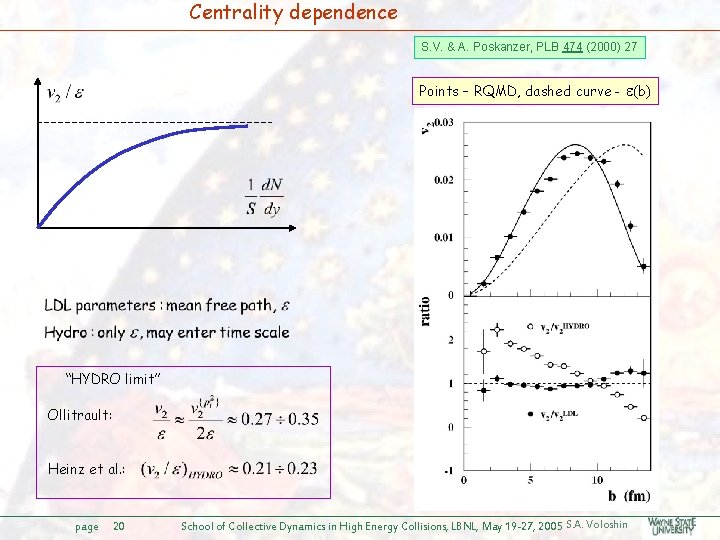
Centrality dependence S. V. & A. Poskanzer, PLB 474 (2000) 27 Points – RQMD, dashed curve - (b) “HYDRO limit” Ollitrault: Heinz et al. : page 20 School of Collective Dynamics in High Energy Collisions, LBNL, May 19 -27, 2005 S. A. Voloshin

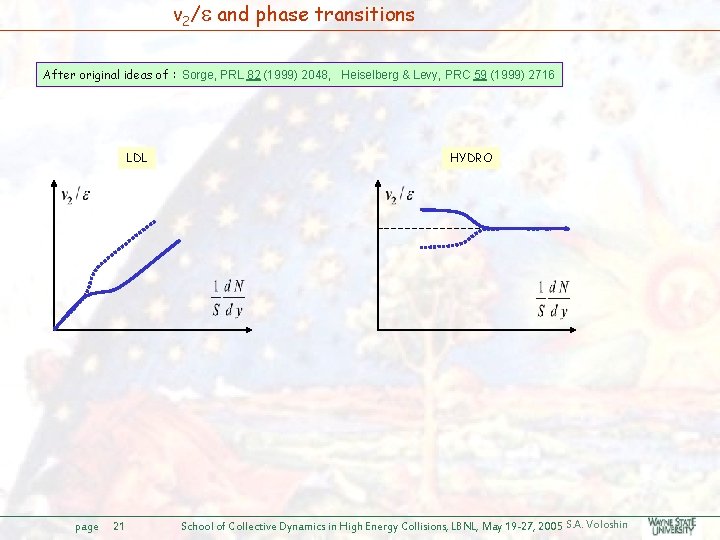
v 2/ and phase transitions After original ideas of : Sorge, PRL 82 (1999) 2048, Heiselberg & Levy, PRC 59 (1999) 2716 LDL page 21 HYDRO School of Collective Dynamics in High Energy Collisions, LBNL, May 19 -27, 2005 S. A. Voloshin

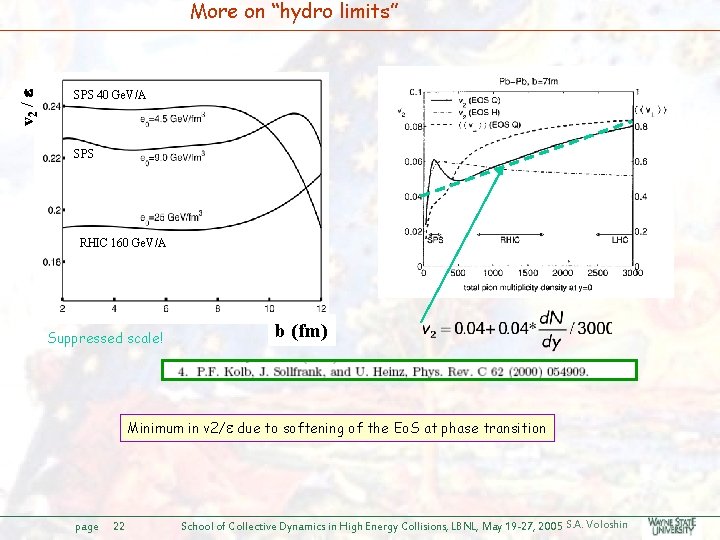
v 2 / More on “hydro limits” SPS 40 Ge. V/A SPS RHIC 160 Ge. V/A Suppressed scale! b (fm) Minimum in v 2/ due to softening of the Eo. S at phase transition page 22 School of Collective Dynamics in High Energy Collisions, LBNL, May 19 -27, 2005 S. A. Voloshin

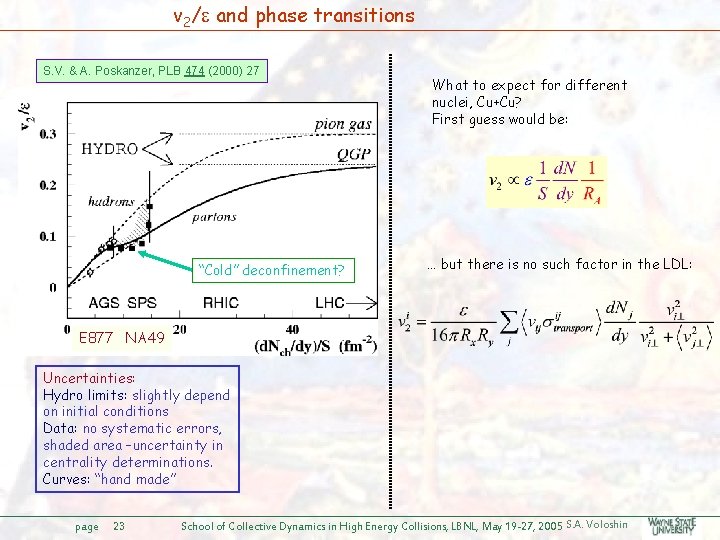
v 2/ and phase transitions S. V. & A. Poskanzer, PLB 474 (2000) 27 “Cold” deconfinement? What to expect for different nuclei, Cu+Cu? First guess would be: … but there is no such factor in the LDL: E 877 NA 49 Uncertainties: Hydro limits: slightly depend on initial conditions Data: no systematic errors, shaded area –uncertainty in centrality determinations. Curves: “hand made” page 23 School of Collective Dynamics in High Energy Collisions, LBNL, May 19 -27, 2005 S. A. Voloshin

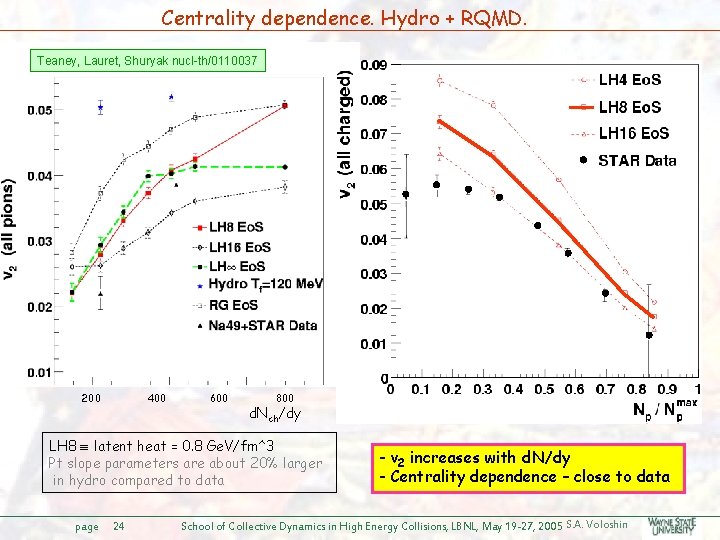
Centrality dependence. Hydro + RQMD. Teaney, Lauret, Shuryak nucl-th/0110037 200 400 600 800 d. Nch/dy LH 8 latent heat = 0. 8 Ge. V/fm^3 Pt slope parameters are about 20% larger in hydro compared to data page 24 - v 2 increases with d. N/dy - Centrality dependence – close to data School of Collective Dynamics in High Energy Collisions, LBNL, May 19 -27, 2005 S. A. Voloshin

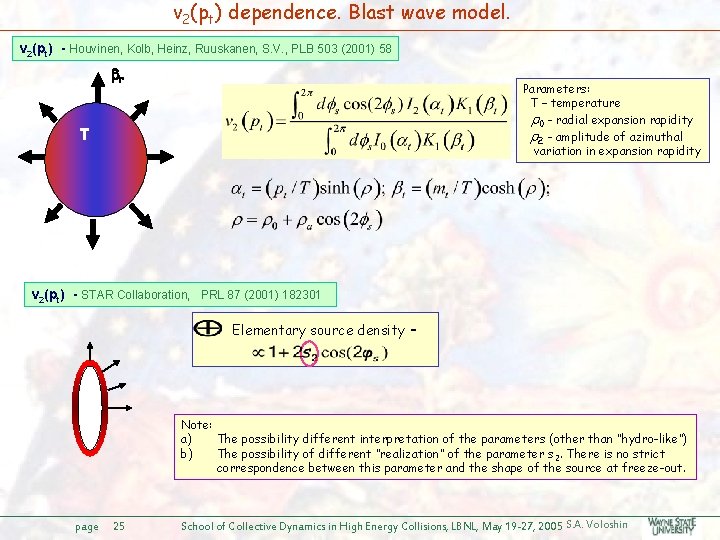
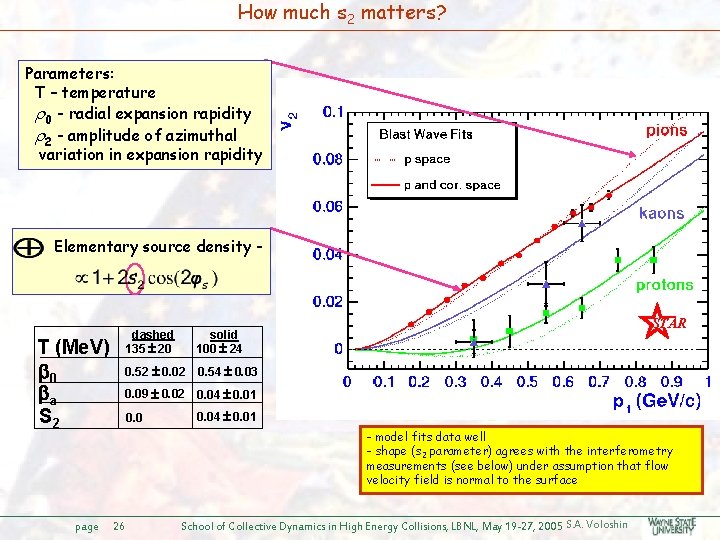
v 2(pt) dependence. Blast wave model. v 2(pt) - Houvinen, Kolb, Heinz, Ruuskanen, S. V. , PLB 503 (2001) 58 r Parameters: T – temperature 0 - radial expansion rapidity 2 - amplitude of azimuthal variation in expansion rapidity T v 2(pt) - STAR Collaboration, PRL 87 (2001) 182301 Elementary source density - Note: a) The possibility different interpretation of the parameters (other than “hydro-like”) b) The possibility of different “realization” of the parameter s 2. There is no strict correspondence between this parameter and the shape of the source at freeze-out. page 25 School of Collective Dynamics in High Energy Collisions, LBNL, May 19 -27, 2005 S. A. Voloshin

How much s 2 matters? Parameters: T – temperature 0 - radial expansion rapidity 2 - amplitude of azimuthal variation in expansion rapidity Elementary source density - T (Me. V) 0 a S 2 page dashed 135 20 solid 100 24 0. 52 0. 02 0. 54 0. 03 STAR 0. 09 0. 02 0. 04 0. 01 - model fits data well - shape (s 2 parameter) agrees with the interferometry measurements (see below) under assumption that flow velocity field is normal to the surface 26 School of Collective Dynamics in High Energy Collisions, LBNL, May 19 -27, 2005 S. A. Voloshin

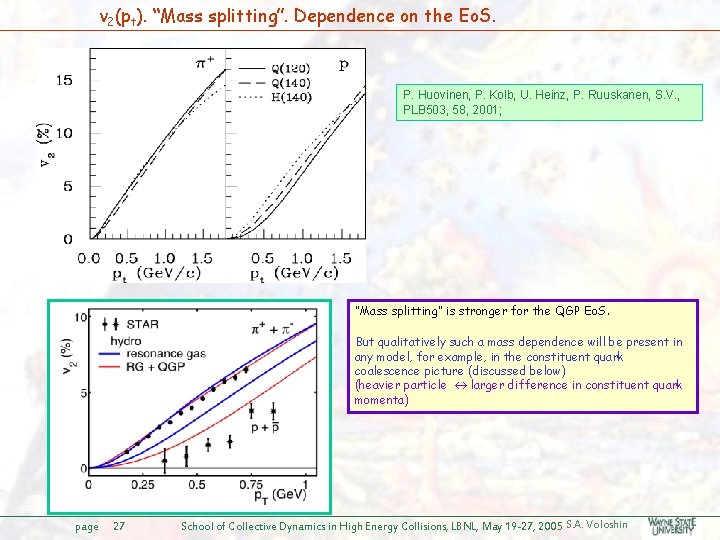
v 2(pt). “Mass splitting”. Dependence on the Eo. S. P. Huovinen, P. Kolb, U. Heinz, P. Ruuskanen, S. V. , PLB 503, 58, 2001; “Mass splitting” is stronger for the QGP Eo. S. But qualitatively such a mass dependence will be present in any model, for example, in the constituent quark coalescence picture (discussed below) (heavier particle larger difference in constituent quark momenta) page 27 School of Collective Dynamics in High Energy Collisions, LBNL, May 19 -27, 2005 S. A. Voloshin

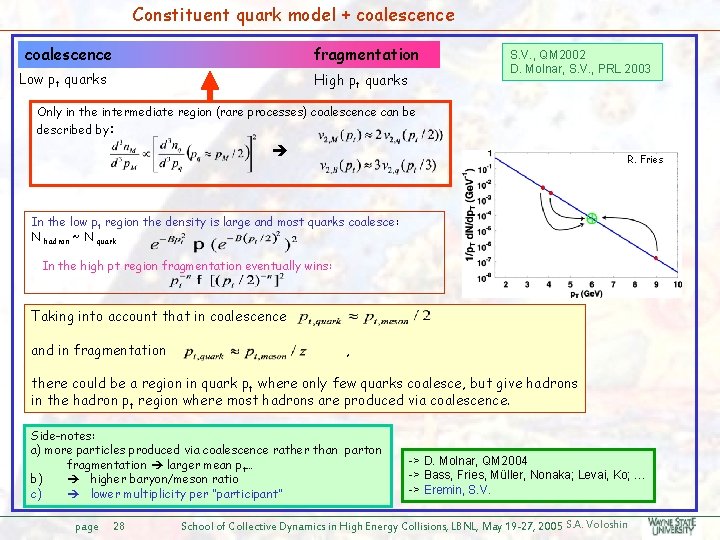
Constituent quark model + coalescence fragmentation Low pt quarks High pt quarks S. V. , QM 2002 D. Molnar, S. V. , PRL 2003 Only in the intermediate region (rare processes) coalescence can be described by: R. Fries In the low pt region the density is large and most quarks coalesce: N hadron ~ N quark In the high pt region fragmentation eventually wins: Taking into account that in coalescence and in fragmentation , there could be a region in quark pt where only few quarks coalesce, but give hadrons in the hadron pt region where most hadrons are produced via coalescence. Side-notes: a) more particles produced via coalescence rather than parton fragmentation larger mean pt… b) higher baryon/meson ratio c) lower multiplicity per “participant” page 28 -> D. Molnar, QM 2004 -> Bass, Fries, Müller, Nonaka; Levai, Ko; … -> Eremin, S. V. School of Collective Dynamics in High Energy Collisions, LBNL, May 19 -27, 2005 S. A. Voloshin

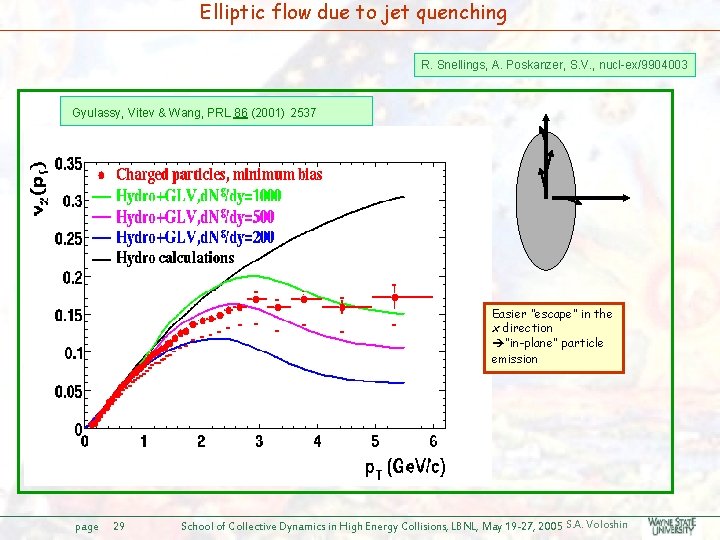
Elliptic flow due to jet quenching R. Snellings, A. Poskanzer, S. V. , nucl-ex/9904003 Gyulassy, Vitev & Wang, PRL 86 (2001) 2537 Easier “escape” in the x direction “in-plane” particle emission page 29 School of Collective Dynamics in High Energy Collisions, LBNL, May 19 -27, 2005 S. A. Voloshin

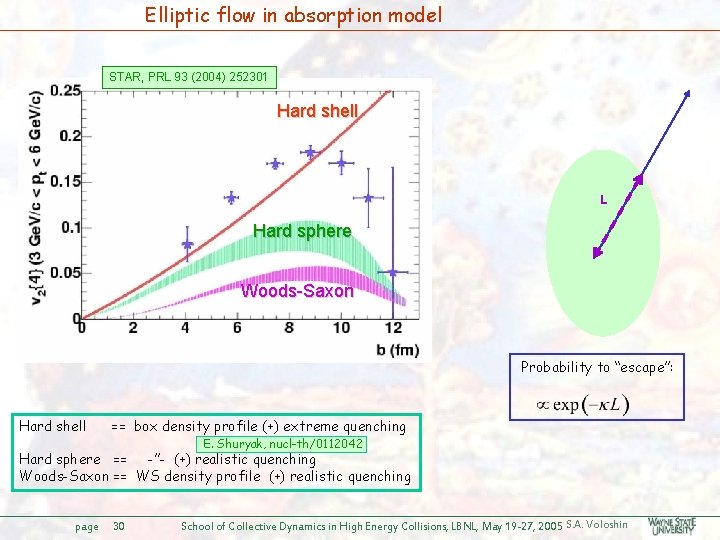
Elliptic flow in absorption model STAR, PRL 93 (2004) 252301 Hard shell L Hard sphere Woods-Saxon Probability to “escape”: Hard shell == box density profile (+) extreme quenching E. Shuryak, nucl-th/0112042 Hard sphere == -”- (+) realistic quenching Woods-Saxon == WS density profile (+) realistic quenching page 30 School of Collective Dynamics in High Energy Collisions, LBNL, May 19 -27, 2005 S. A. Voloshin

New possibilities Anisotropies and asymmetries 1. 2. 3. 4. 5. page 31 HBT with respect to the reaction plane Non-identical particle correlations with respect to the reaction plane High pt 2 -particle correlation wrt reaction plane Global polarization in AA Parity violation School of Collective Dynamics in High Energy Collisions, LBNL, May 19 -27, 2005 S. A. Voloshin

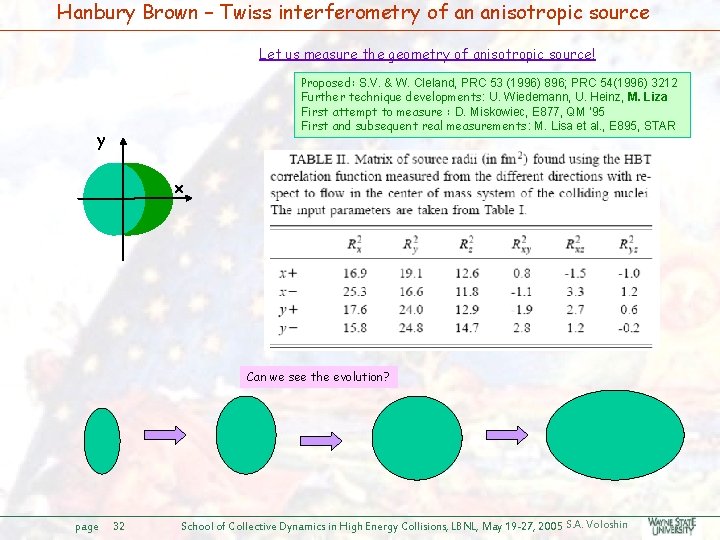
Hanbury Brown – Twiss interferometry of an anisotropic source Let us measure the geometry of anisotropic source! Proposed: S. V. & W. Cleland, PRC 53 (1996) 896; PRC 54(1996) 3212 Further technique developments: U. Wiedemann, U. Heinz, M. Liza First attempt to measure : D. Miskowiec, E 877, QM ’ 95 First and subsequent real measurements: M. Lisa et al. , E 895, STAR y x Can we see the evolution? page 32 School of Collective Dynamics in High Energy Collisions, LBNL, May 19 -27, 2005 S. A. Voloshin

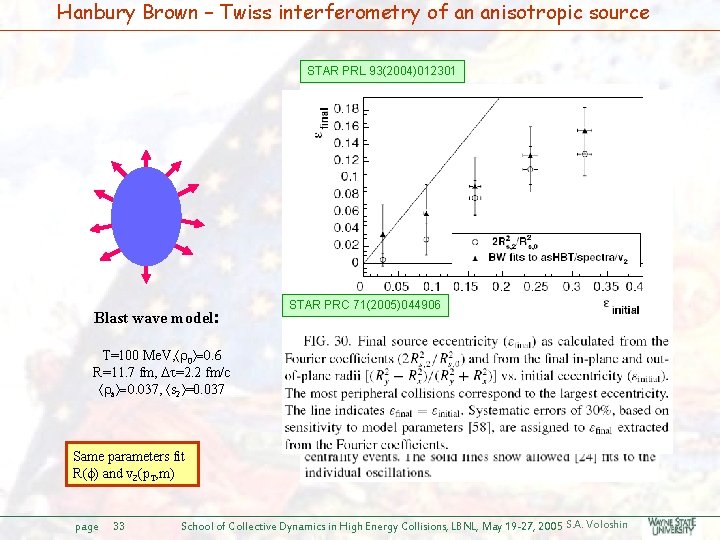
Hanbury Brown – Twiss interferometry of an anisotropic source STAR PRL 93(2004)012301 Blast wave model: STAR PRC 71(2005)044906 T=100 Me. V, r 0 =0. 6 R=11. 7 fm, Dt=2. 2 fm/c ra =0. 037, s 2 =0. 037 Same parameters fit R(f) and v 2(p. T, m) page 33 School of Collective Dynamics in High Energy Collisions, LBNL, May 19 -27, 2005 S. A. Voloshin

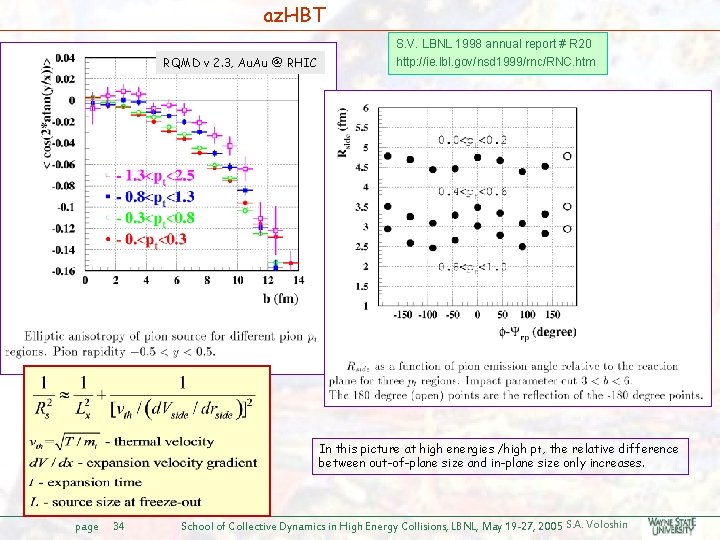
az. HBT RQMD v 2. 3, Au. Au @ RHIC S. V. LBNL 1998 annual report # R 20 http: //ie. lbl. gov/nsd 1999/rnc/RNC. htm In this picture at high energies /high pt, the relative difference between out-of-plane size and in-plane size only increases. page 34 School of Collective Dynamics in High Energy Collisions, LBNL, May 19 -27, 2005 S. A. Voloshin

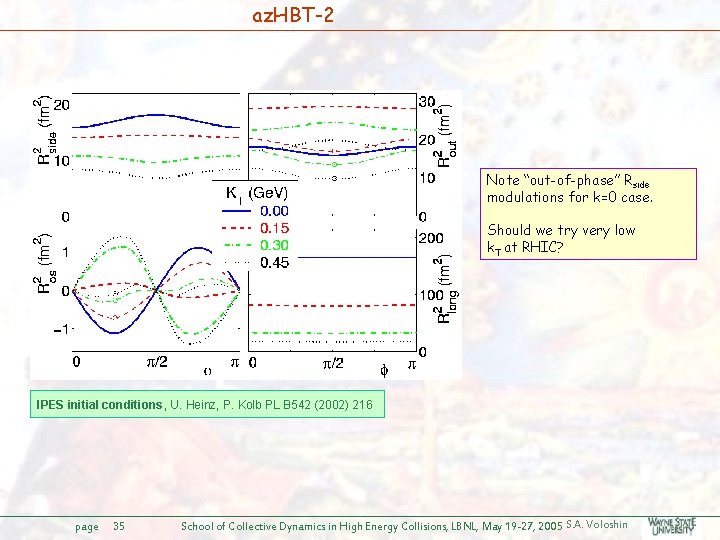
az. HBT-2 Note “out-of-phase” Rside modulations for k=0 case. Should we try very low k. T at RHIC? IPES initial conditions, U. Heinz, P. Kolb PL B 542 (2002) 216 page 35 School of Collective Dynamics in High Energy Collisions, LBNL, May 19 -27, 2005 S. A. Voloshin

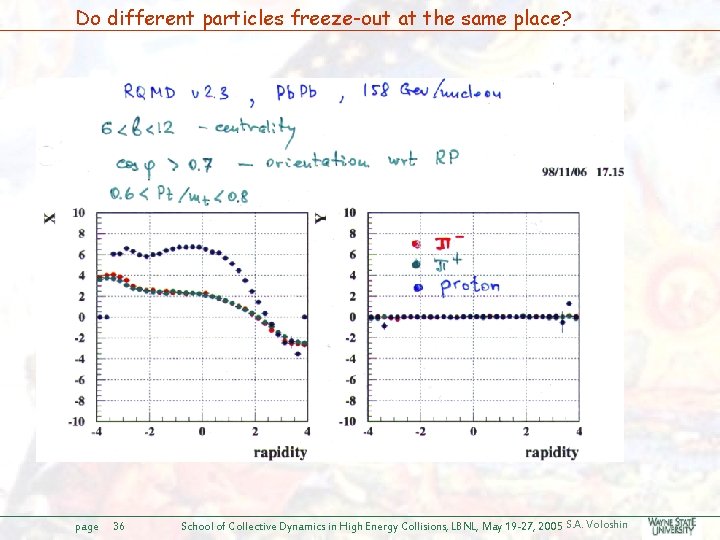
Do different particles freeze-out at the same place? page 36 School of Collective Dynamics in High Energy Collisions, LBNL, May 19 -27, 2005 S. A. Voloshin

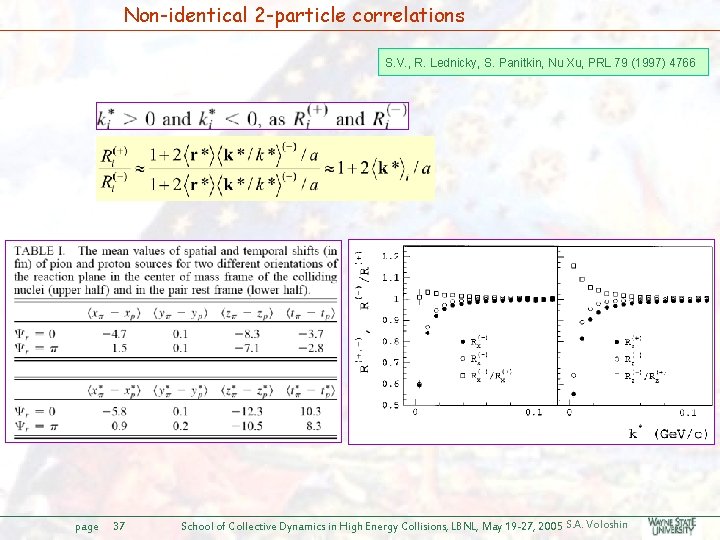
Non-identical 2 -particle correlations S. V. , R. Lednicky, S. Panitkin, Nu Xu, PRL 79 (1997) 4766 page 37 School of Collective Dynamics in High Energy Collisions, LBNL, May 19 -27, 2005 S. A. Voloshin

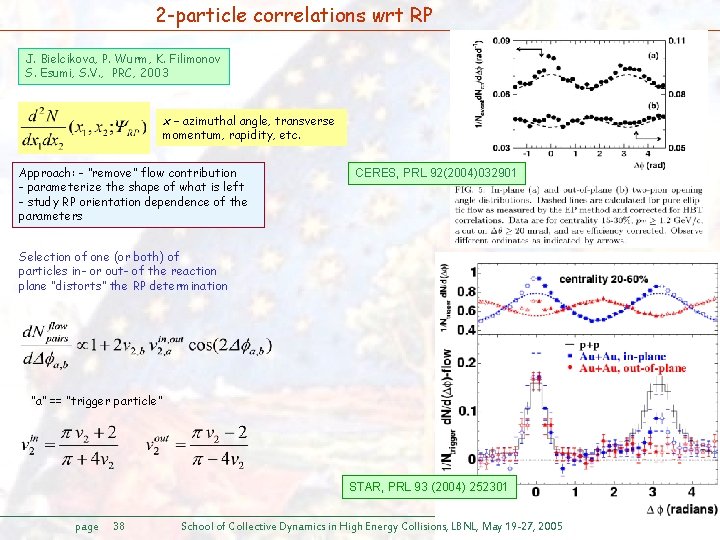
2 -particle correlations wrt RP J. Bielcikova, P. Wurm, K. Filimonov S. Esumi, S. V. , PRC, 2003 x – azimuthal angle, transverse momentum, rapidity, etc. Approach: - “remove” flow contribution - parameterize the shape of what is left - study RP orientation dependence of the parameters CERES, PRL 92(2004)032901 Selection of one (or both) of particles in- or out- of the reaction plane “distorts” the RP determination “a” == “trigger particle” STAR, PRL 93 (2004) 252301 page 38 School of Collective Dynamics in High Energy Collisions, LBNL, May 19 -27, 2005 S. A. Voloshin

Parity, CP- violation, global polarization… Kharzeev, Pisarski, Tytgat, PRL 81 (1998) 512 Kharzeev, Pisarski, PRD 61 (2000) 111901 Observing parity (CP) violation with anisotropic flow techniques Parity violation S. V. PRC 62 (2000) 044901 D. Kharzeev, hep-ph/0406125 : Emission of positive (negative) pions could be asymmetric along the system angular momentum S. V. PRC 70 (2004) 057901 Global polarization Liang, Wang, nucl-th: 0410079. PRL S. V. nucl-th: 0410089 Large orbital momentum of the system can be transformed into particle spin momentum global polarization “Oriented” DCC Asakawa, Minakata, Müller, nucl-th/0212070 Negative elliptic flow of neutral pions page 39 School of Collective Dynamics in High Energy Collisions, LBNL, May 19 -27, 2005 S. A. Voloshin

How one would measure flow? page 40 School of Collective Dynamics in High Energy Collisions, LBNL, May 19 -27, 2005 S. A. Voloshin

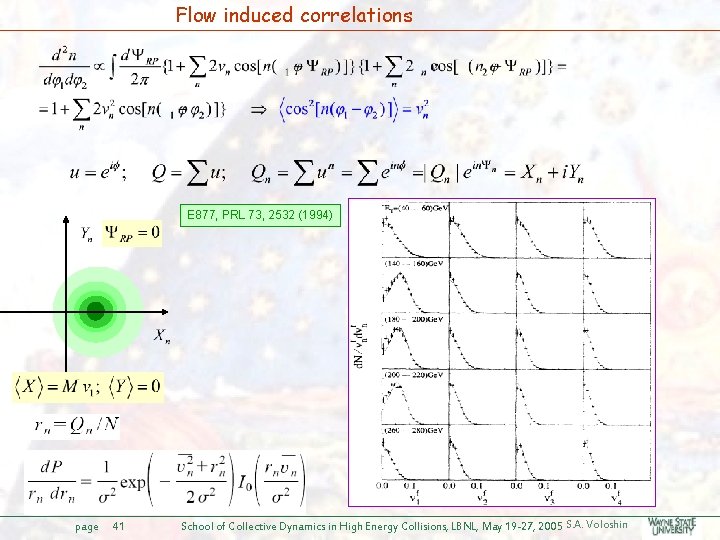
Flow induced correlations E 877, PRL 73, 2532 (1994) page 41 School of Collective Dynamics in High Energy Collisions, LBNL, May 19 -27, 2005 S. A. Voloshin

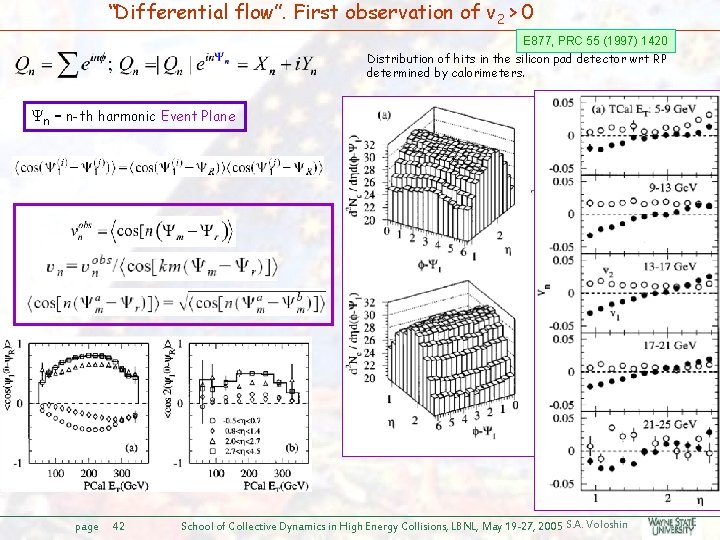
“Differential flow”. First observation of v 2 > 0 E 877, PRC 55 (1997) 1420 Distribution of hits in the silicon pad detector wrt RP determined by calorimeters. n – n-th harmonic Event Plane page 42 School of Collective Dynamics in High Energy Collisions, LBNL, May 19 -27, 2005 S. A. Voloshin

End of the ideal world: “Non-flow”, flow fluctuations, … Flow “non-flow” “Non-flow” – azimuthal correlations of any other origin except the correlation with respect to the reaction plane. It combines the possible contributions from resonance decay, inter and intra jet correlations, etc. An example: Effect of flow fluctuations Other possibilities fro flow fluctuations: fluctuation in the initial geometry, in multiplicity at the same geometry, etc. Not perfect azimuthal acceptance not flat Event Plane distribution. “Flattening of the reaction plane”. Approximate and exact solutions to the problem. Each one by itself presents little problem, but taken at the same time, it is the major problem we fight during the last years. page 43 School of Collective Dynamics in High Energy Collisions, LBNL, May 19 -27, 2005 S. A. Voloshin

Part I. The End. Part II. Methods and Results 1. Non-flow estimates - From the “resolution plot” - Azimuthal correlations in pp and AA 2. Multiparticle correlations - 4 -particle cumulants. Methods. - Non-flow and flow fluctuations - Mixed harmonics. 3 -particle correlations. - Distributions in q-vector - Detector effects 3. Main results - Reaching the hydro limit - Mass splitting - Constituent quark scaling - Elliptic flow at high pt - v 1 and higher harmonics - other 4. Conclusion page 44 School of Collective Dynamics in High Energy Collisions, LBNL, May 19 -27, 2005 S. A. Voloshin

EXTRA page 45 School of Collective Dynamics in High Energy Collisions, LBNL, May 19 -27, 2005 S. A. Voloshin

Mixed harmonic technique or 3 -particle correlations hep-ph/0406311 a > 0 preferential emission along the angular momentum The sign can vary event by event, a~Q/N , where Q is the topological charge, |Q|=1, 2, … at d. N/dy~100, |a|~1%. projections onto reaction plane Projections on the direction of angular momentum All effects non sensitive to the RP cancel out! Possible systematics: clusters that flow And using only one particle instead of the event flow vector note that for a rapidity region symmetric with respect to the midrapidity v 1=0 page 46 School of Collective Dynamics in High Energy Collisions, LBNL, May 19 -27, 2005 S. A. Voloshin

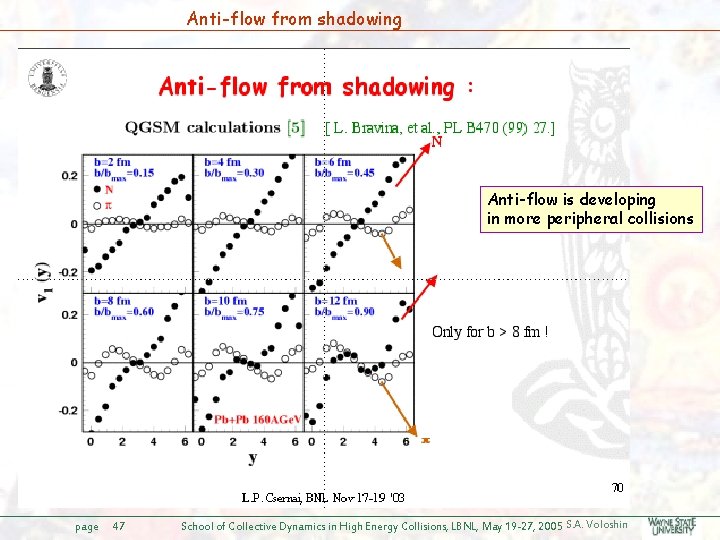
Anti-flow from shadowing Anti-flow is developing in more peripheral collisions page 47 School of Collective Dynamics in High Energy Collisions, LBNL, May 19 -27, 2005 S. A. Voloshin

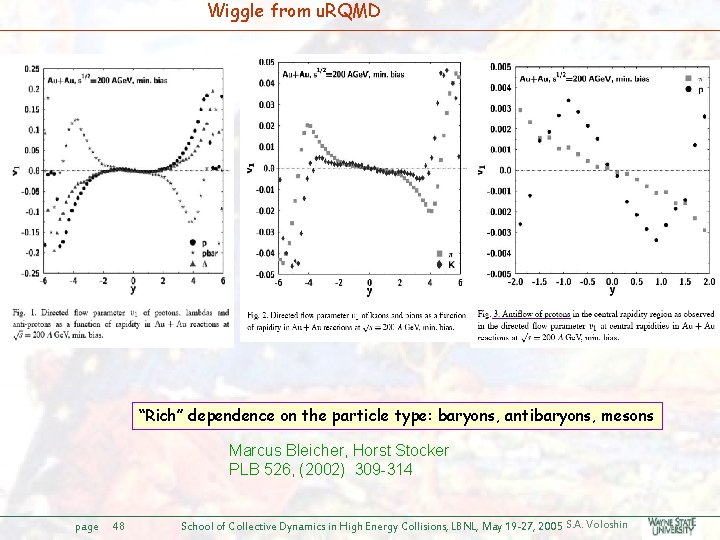
Wiggle from u. RQMD “Rich” dependence on the particle type: baryons, antibaryons, mesons Marcus Bleicher, Horst Stocker PLB 526, (2002) 309 -314 page 48 School of Collective Dynamics in High Energy Collisions, LBNL, May 19 -27, 2005 S. A. Voloshin

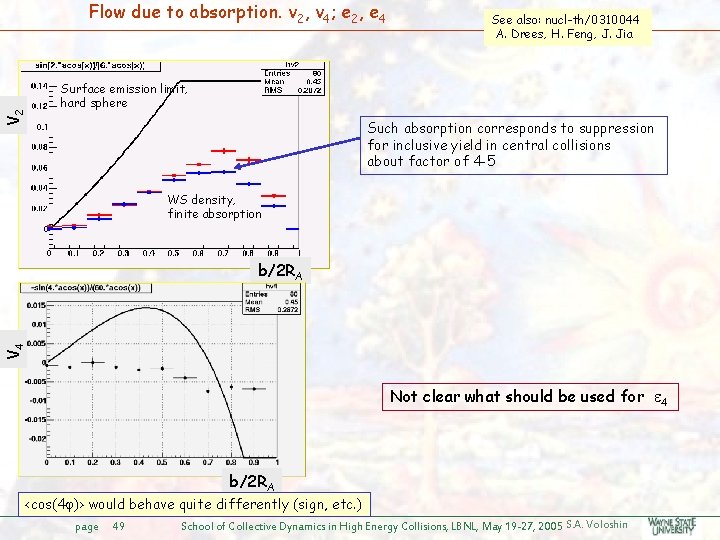
V 2 Flow due to absorption. v 2, v 4; e 2, e 4 See also: nucl-th/0310044 A. Drees, H. Feng, J. Jia Surface emission limit, hard sphere Such absorption corresponds to suppression for inclusive yield in central collisions about factor of 4 -5 WS density, finite absorption V 4 b/2 RA Not clear what should be used for 4 b/2 RA <cos(4 )> would behave quite differently (sign, etc. ) page 49 School of Collective Dynamics in High Energy Collisions, LBNL, May 19 -27, 2005 S. A. Voloshin