ANGULOS y sus aplicaciones copywriter 1 ANGULO Es

ANGULOS y sus aplicaciones © copywriter 1

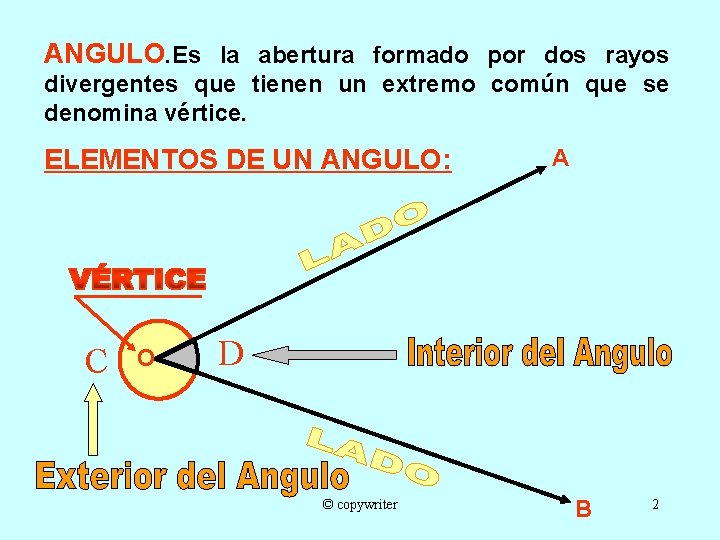
ANGULO. Es la abertura formado por dos rayos divergentes que tienen un extremo común que se denomina vértice. ELEMENTOS DE UN ANGULO: C O A D © copywriter B 2

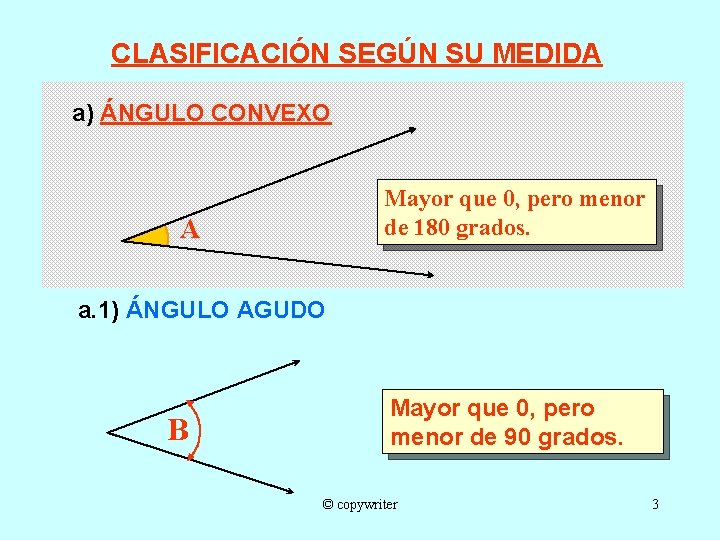
CLASIFICACIÓN SEGÚN SU MEDIDA a) ÁNGULO CONVEXO Mayor que 0, pero menor de 180 grados. A a. 1) ÁNGULO AGUDO B Mayor que 0, pero menor de 90 grados. © copywriter 3

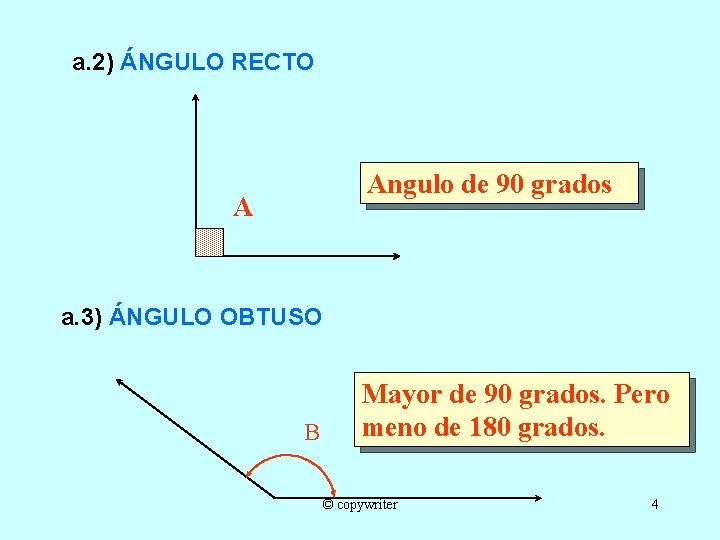
a. 2) ÁNGULO RECTO Angulo de 90 grados A a. 3) ÁNGULO OBTUSO B Mayor de 90 grados. Pero meno de 180 grados. © copywriter 4

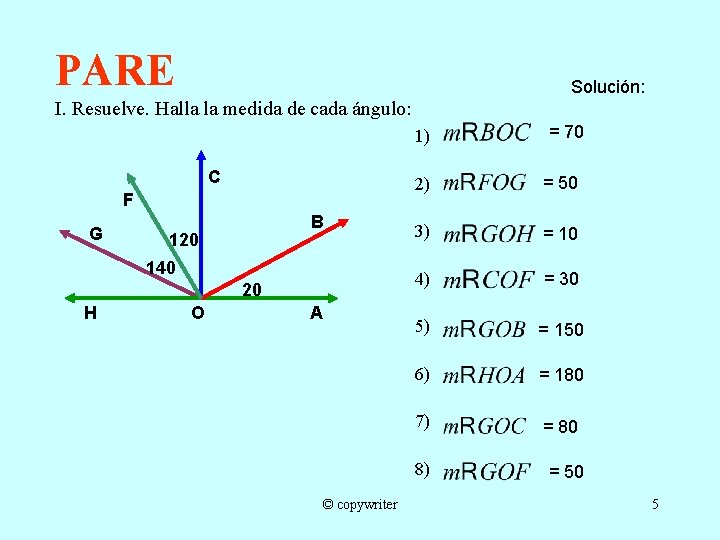
PARE Solución: I. Resuelve. Halla la medida de cada ángulo: 1) C F G B 120 140 20 H O A 2) = 50 3) = 10 4) = 30 5) = 150 6) = 180 7) = 80 8) © copywriter = 70 = 50 5

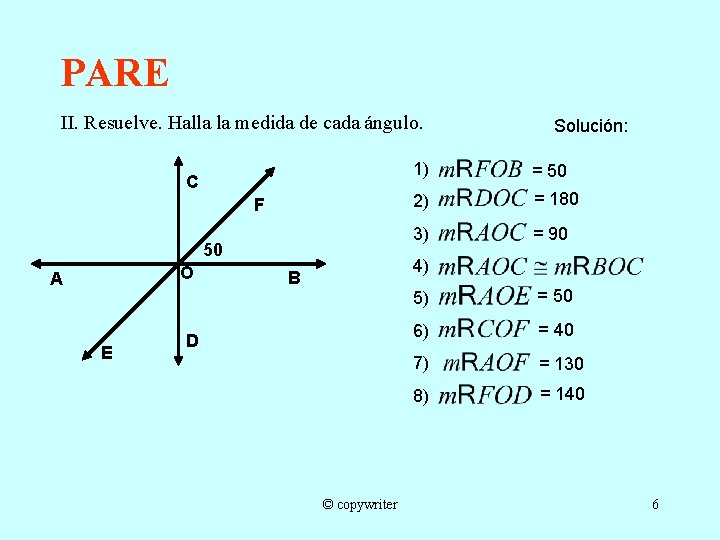
PARE II. Resuelve. Halla la medida de cada ángulo. C F 50 O A E Solución: 1) = 50 2) = 180 3) = 90 4) B D © copywriter 5) = 50 6) = 40 7) = 130 8) = 140 6

Práctica adícional: (Relación de ángulos): z `125 x y Solución: X = 125 Opuestos por el vértice. Y = 55 Par lineal con 125 o con x. Z = 55 Opuesto por el vértice o par lineal. © copywriter 7

Tema: Relación Entre Angulos © copywriter 8

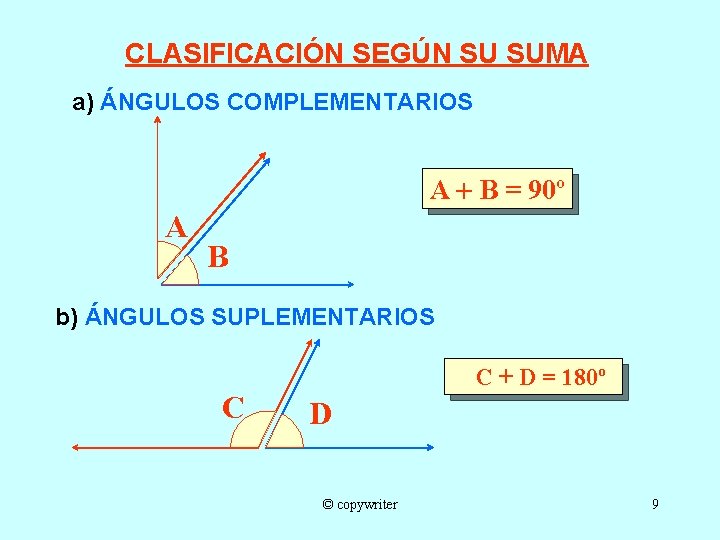
CLASIFICACIÓN SEGÚN SU SUMA a) ÁNGULOS COMPLEMENTARIOS A B = 90º A B b) ÁNGULOS SUPLEMENTARIOS C C + D = 180º D © copywriter 9

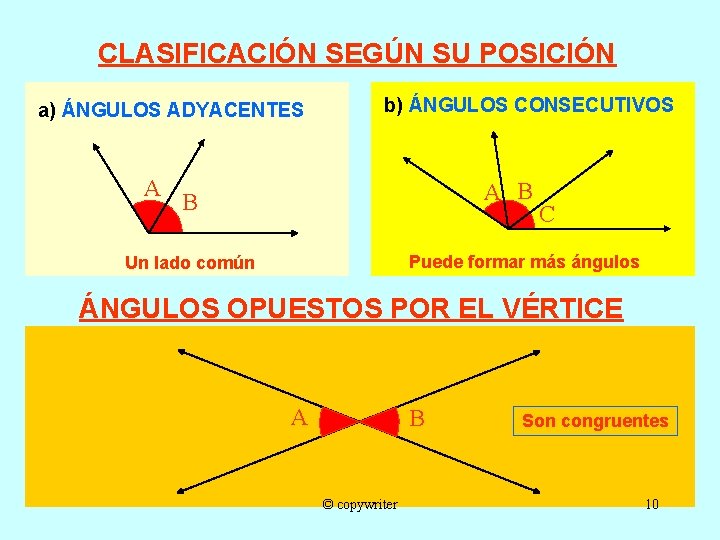
CLASIFICACIÓN SEGÚN SU POSICIÓN a) ÁNGULOS ADYACENTES A b) ÁNGULOS CONSECUTIVOS A B B C Puede formar más ángulos Un lado común ÁNGULOS OPUESTOS POR EL VÉRTICE A B © copywriter Son congruentes 10

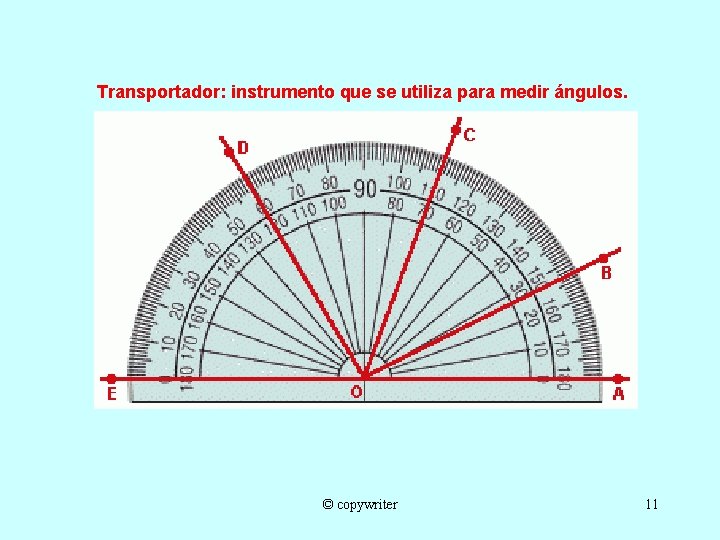
Transportador: instrumento que se utiliza para medir ángulos. © copywriter 11

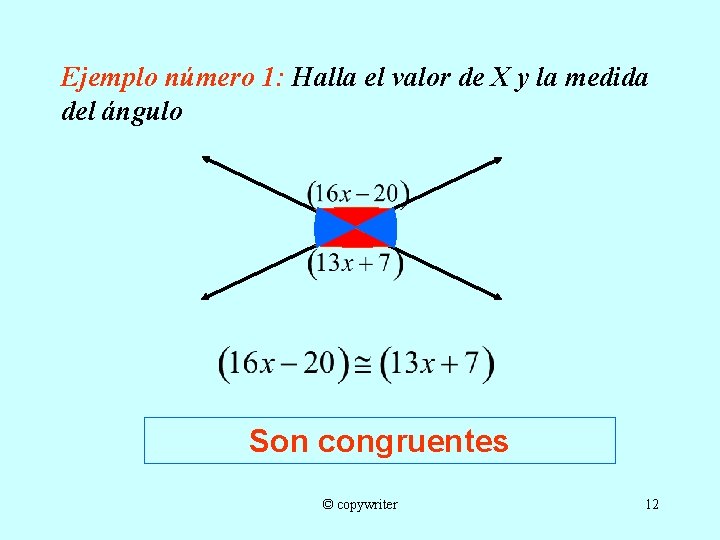
Ejemplo número 1: Halla el valor de X y la medida del ángulo Son congruentes © copywriter 12

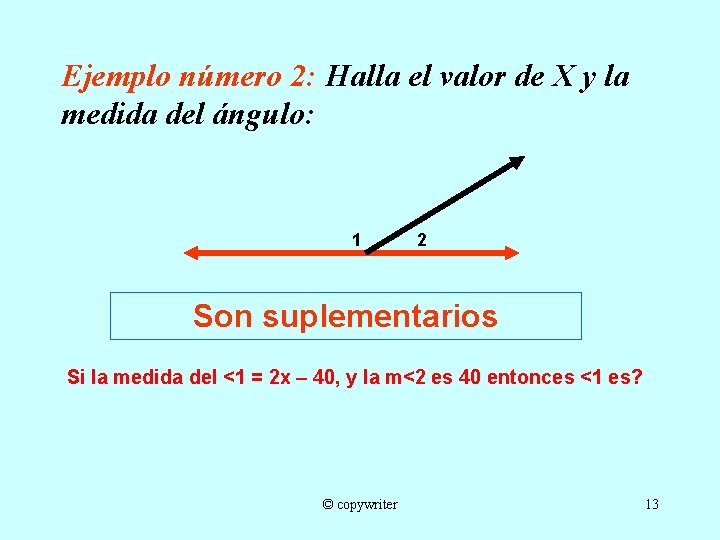
Ejemplo número 2: Halla el valor de X y la medida del ángulo: 1 2 Son suplementarios Si la medida del <1 = 2 x – 40, y la m<2 es 40 entonces <1 es? © copywriter 13

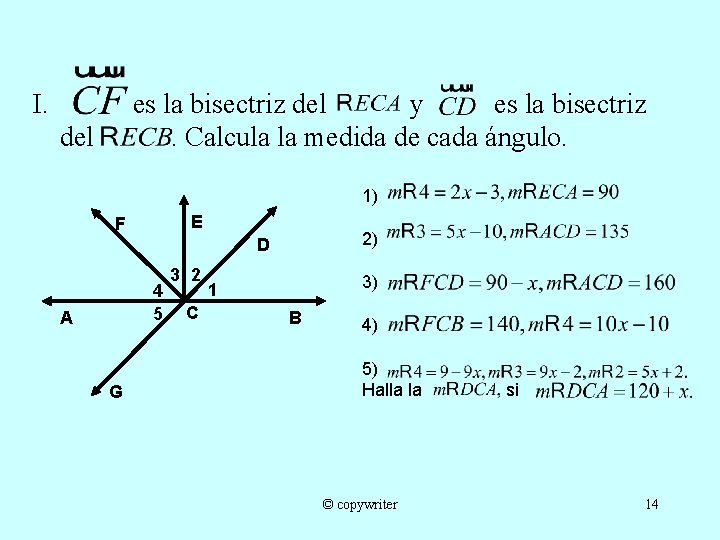
I. es la bisectriz del y es la bisectriz. Calcula la medida de cada ángulo. del 1) E F 2) D 4 5 A G 3 2 C 3) 1 B 4) 5) Halla la © copywriter si 14

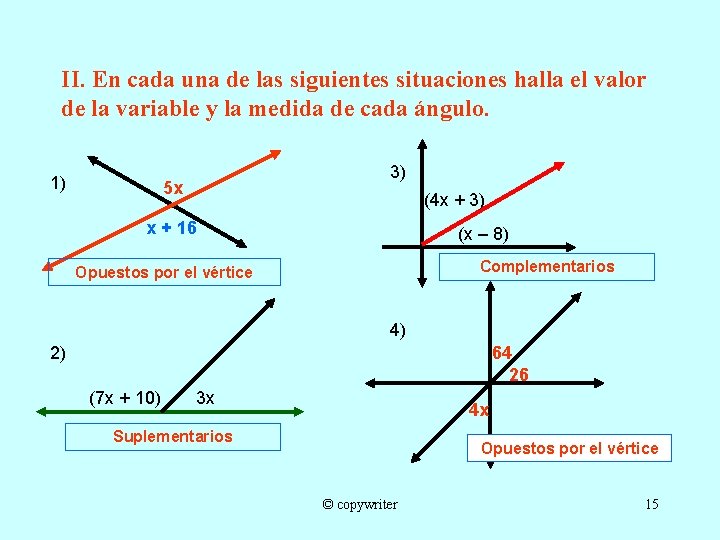
II. En cada una de las siguientes situaciones halla el valor de la variable y la medida de cada ángulo. 1) 3) 5 x (4 x + 3) x + 16 (x – 8) Complementarios Opuestos por el vértice 4) 64 26 2) (7 x + 10) 3 x 4 x Suplementarios Opuestos por el vértice © copywriter 15

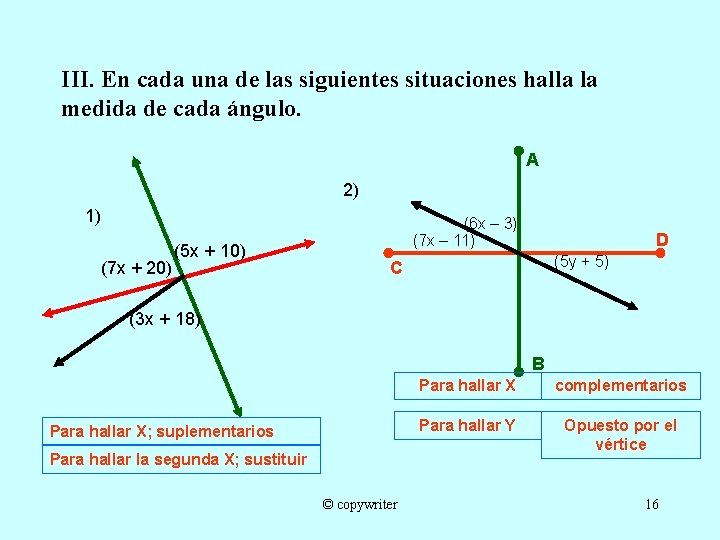
III. En cada una de las siguientes situaciones halla la medida de cada ángulo. A 2) 1) (7 x + 20) (5 x + 10) (6 x – 3) (7 x – 11) D (5 y + 5) C (3 x + 18) B Para hallar X; suplementarios Para hallar la segunda X; sustituir © copywriter Para hallar X complementarios Para hallar Y Opuesto por el vértice 16

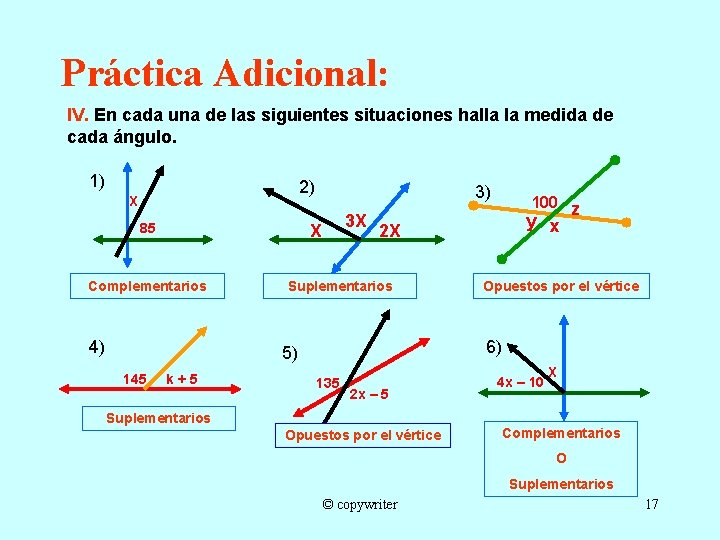
Práctica Adicional: IV. En cada una de las siguientes situaciones halla la medida de cada ángulo. 1) 2) X 85 3) 3 X X Complementarios 4) k+5 y x 2 X Suplementarios Opuestos por el vértice 6) 5) 145 100 z 135 2 x – 5 Suplementarios Opuestos por el vértice 4 x – 10 X Complementarios O Suplementarios © copywriter 17

Tema: Rectas Paralelas & Transversales © copywriter 18

Introducción Cuando dos planos no se intersecan, reciben el nombre planos paralelos. De la misma manera son paralelas rectas en un mismo plano que no se intersecan. Pero cuando estas no estan en el mismo plano y no se intersecan reciben el nombre de rectas alabeadas o rectas oblicuas. Una recta que interseca dos o más rectas en un mismo plano y en puntos distintos recibe el nombre de transversal. © copywriter 19

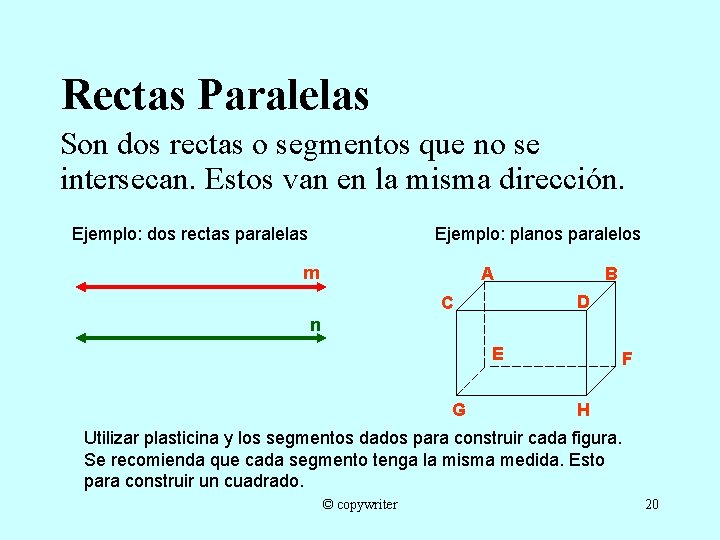
Rectas Paralelas Son dos rectas o segmentos que no se intersecan. Estos van en la misma dirección. Ejemplo: dos rectas paralelas Ejemplo: planos paralelos m A B D C n E G F H Utilizar plasticina y los segmentos dados para construir cada figura. Se recomienda que cada segmento tenga la misma medida. Esto para construir un cuadrado. © copywriter 20

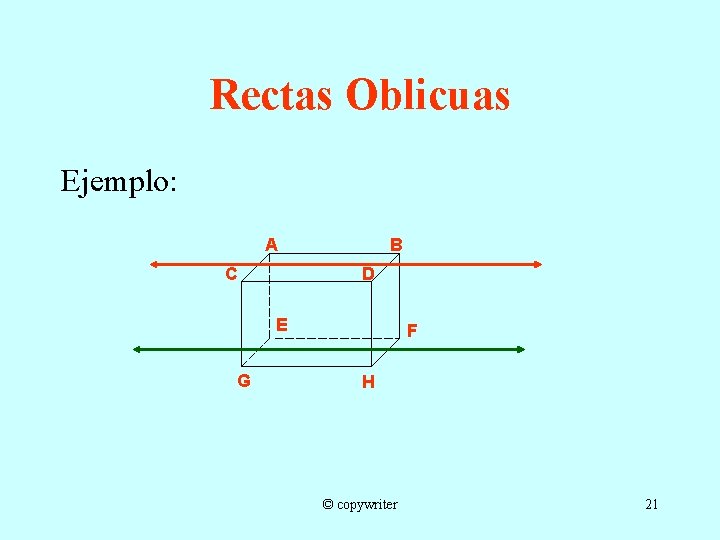
Rectas Oblicuas Ejemplo: A B D C E G F H © copywriter 21

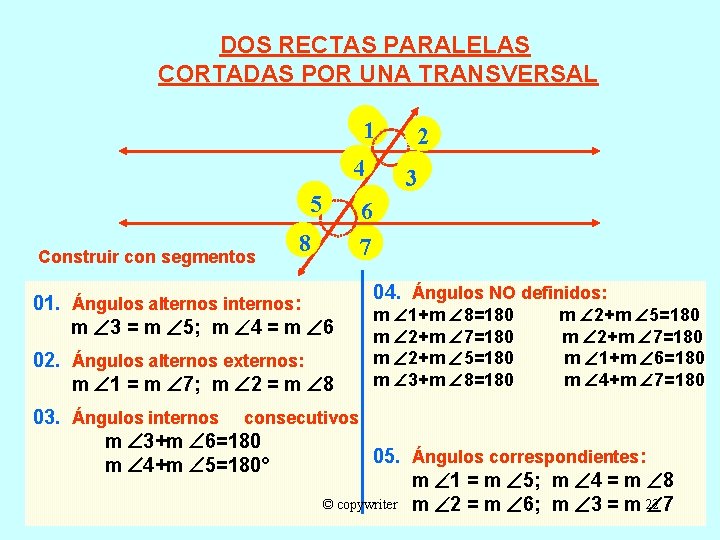
DOS RECTAS PARALELAS CORTADAS POR UNA TRANSVERSAL 1 4 5 Construir con segmentos 8 01. Ángulos alternos internos: m 3 = m 5; m 4 = m 6 02. Ángulos alternos externos: m 1 = m 7; m 2 = m 8 2 3 6 7 04. Ángulos NO definidos: m 1+m 8=180 m 2+m 7=180 m 2+m 5=180 m 3+m 8=180 m 2+m 5=180 m 2+m 7=180 m 1+m 6=180 m 4+m 7=180 03. Ángulos internos consecutivos: m 3+m 6=180 05. Ángulos correspondientes: m 4+m 5=180° m 1 = m 5; m 4 = m 8 © copywriter m 2 = m 6; m 3 = m 22 7

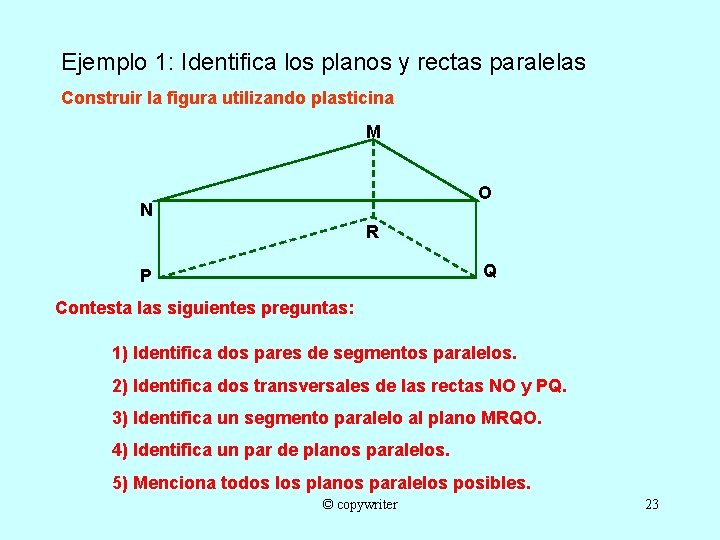
Ejemplo 1: Identifica los planos y rectas paralelas Construir la figura utilizando plasticina M O N R Q P Contesta las siguientes preguntas: 1) Identifica dos pares de segmentos paralelos. 2) Identifica dos transversales de las rectas NO y PQ. 3) Identifica un segmento paralelo al plano MRQO. 4) Identifica un par de planos paralelos. 5) Menciona todos los planos paralelos posibles. © copywriter 23

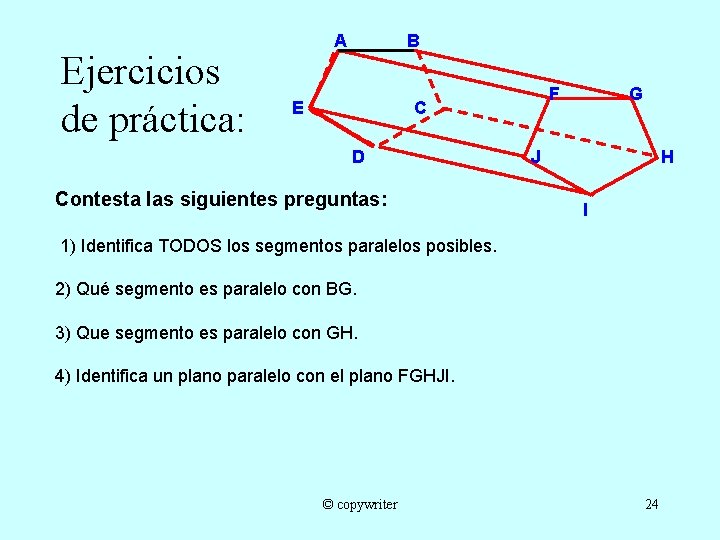
Ejercicios de práctica: A B E F C D Contesta las siguientes preguntas: G J H I 1) Identifica TODOS los segmentos paralelos posibles. 2) Qué segmento es paralelo con BG. 3) Que segmento es paralelo con GH. 4) Identifica un plano paralelo con el plano FGHJI. © copywriter 24

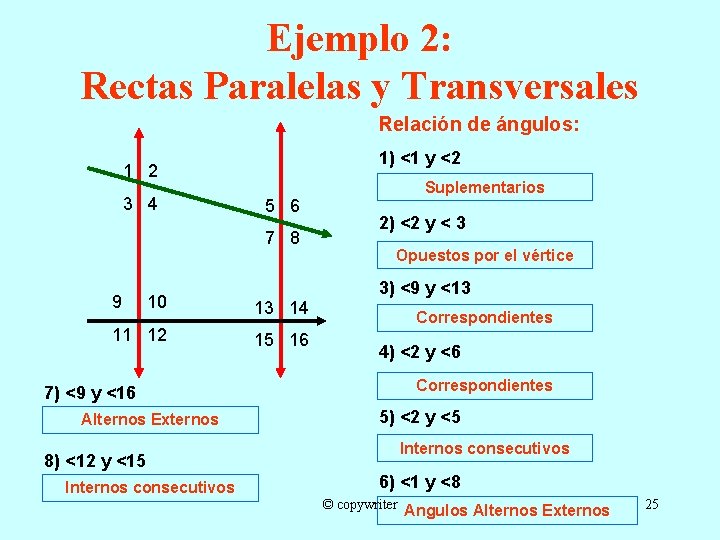
Ejemplo 2: Rectas Paralelas y Transversales Relación de ángulos: 1) <1 y <2 1 2 3 4 5 6 7 8 9 13 14 11 12 15 16 Alternos Externos 8) <12 y <15 Internos consecutivos 2) <2 y < 3 Opuestos por el vértice 3) <9 y <13 10 7) <9 y <16 Suplementarios Correspondientes 4) <2 y <6 Correspondientes 5) <2 y <5 Internos consecutivos 6) <1 y <8 © copywriter Angulos Alternos Externos 25

Angulos y Rectas Paralelas • Si dos rectas paralelas son cortadas por una transversal entonces los siguientes pares de ángulos son congruentes. © copywriter 26

RELACION SEGUN SU MEDIDA (Congruencia) • Angulos que tienen la misma medida: – Angulos alternos internos – Angulos alternos externos – Angulos correspondientes – Angulos opuestos por el vértice © copywriter 27

RELACION SEGUN SU MEDIDA (Suplementarios) • Angulos que la suma de sus medidas es 180: – Par lineal – Internos consecutivos – Angulos NO Definidos © copywriter 28

Ejercicio de práctica: En la figura, N es paralelo con O. Halla la medida de cada ángulo: t 1 2 3 4 4) Si la m<4 = 20, halla la m<7. n 8 7 6 No Definidos 5) Si la m<3 = 140, halla la m<8. o 5 No Definidos 6) Si la m<4 = 30, halla la m<1. No Definidos Resuelve: 7) Si la m<4 = 40, halla la m<2. 1) Si la m<7 = 100, halla la m<3. Correspondientes Alternos Internos 8) Si la m<7 = 125, halla la m<4. 2) Si la m<7 = 95, halla la m<6. No definidos Consecutivos 9) Si la m<1 + m<3 = 230, halla la m<6. 3) Si la m<1 = 120, halla la m<5. Alterno Externos © copywriter Par lineal o Suplementario 29

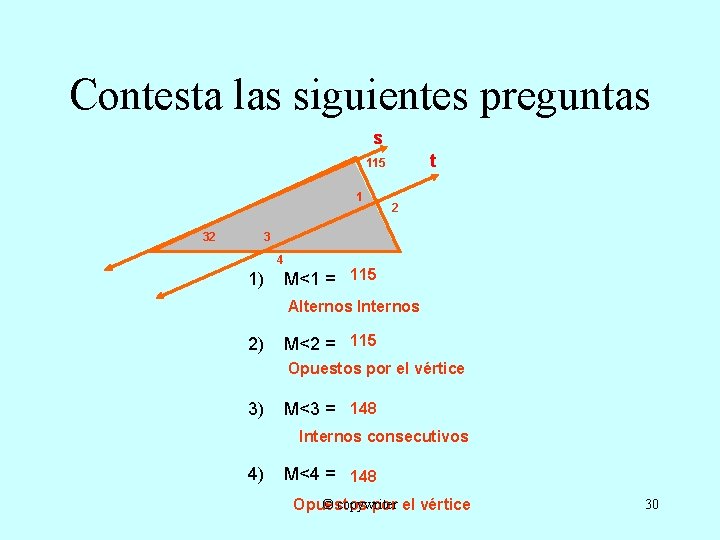
Contesta las siguientes preguntas s t 115 1 32 2 3 4 1) M<1 = 115 Alternos Internos 2) M<2 = 115 Opuestos por el vértice 3) M<3 = 148 Internos consecutivos 4) M<4 = 148 © copywriter Opuestos por el vértice 30

Opcional: Halla la relación de ángulos 1 8 2 3 7 6 15 16 14 1) 13 9 11 4 r 5 10 s 12 l m Angulos Alternos Externos 3 y 12; 4 y 11; 1 y 13; 2 y 14; 2) Angulos Internos Consecutivos 8 y 15; 7 y 16; 6 y 9; 5 y 10; 7 y 6; 16 y 9; 2 y 3; 13 y 11 3) Angulos Alternos Internos 8 y 16; 7 y 15; 6 y 10; 5 y 9 4) Angulos Correspondientes 1 y 15; 8 y 14; 2 y 16; 7 y 13; 3 y 9; 6 y 11; 4 y 10; 5 y 12 1 y 3; 2 y 4; 8 y 6; 7 y 5; 15 y 9; 16 © y copywriter 10; 14 y 11; 13 y 12 31

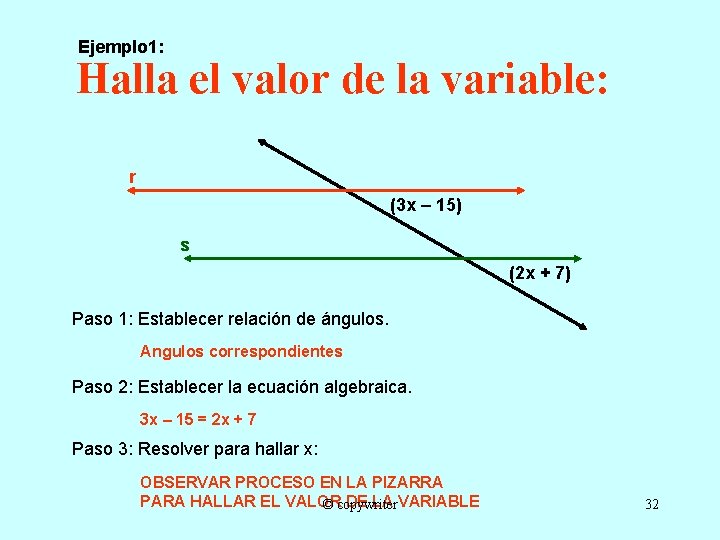
Ejemplo 1: Halla el valor de la variable: r (3 x – 15) s (2 x + 7) Paso 1: Establecer relación de ángulos. Angulos correspondientes Paso 2: Establecer la ecuación algebraica. 3 x – 15 = 2 x + 7 Paso 3: Resolver para hallar x: OBSERVAR PROCESO EN LA PIZARRA PARA HALLAR EL VALOR DE LA VARIABLE © copywriter 32

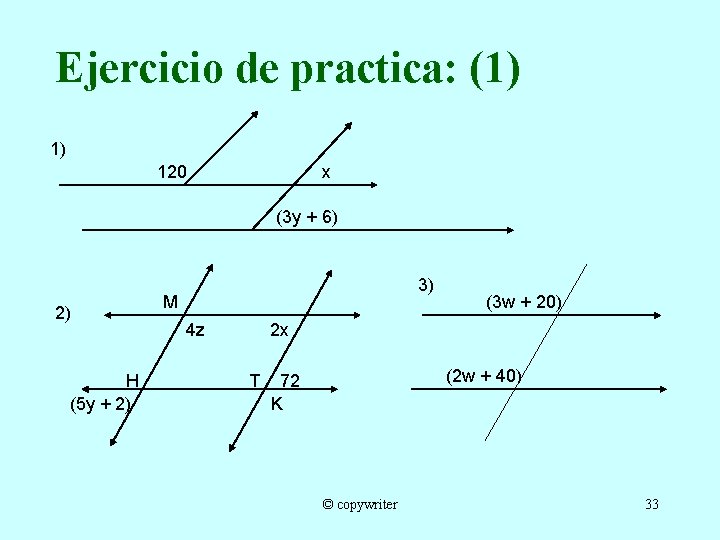
Ejercicio de practica: (1) 1) 120 x (3 y + 6) 2) H (5 y + 2) 3) M 4 z (3 w + 20) 2 x T (2 w + 40) 72 K © copywriter 33

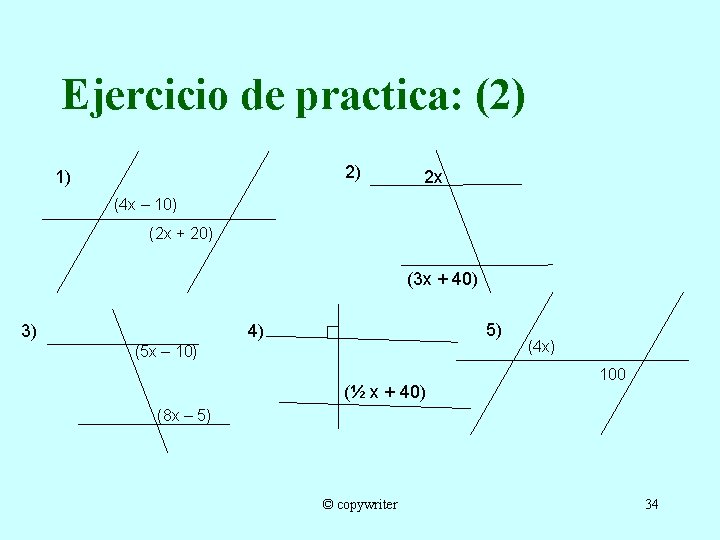
Ejercicio de practica: (2) 2) 1) 2 x (4 x – 10) (2 x + 20) (3 x + 40) 3) 5) 4) (5 x – 10) (½ x + 40) (4 x) 100 (8 x – 5) © copywriter 34

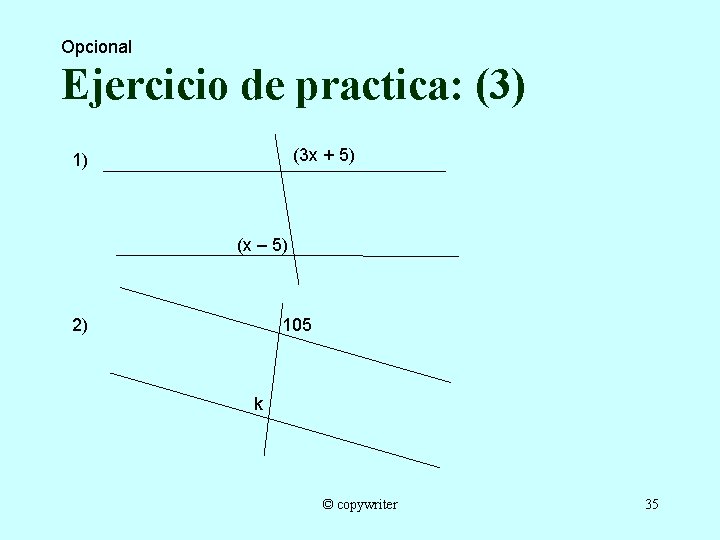
Opcional Ejercicio de practica: (3) (3 x + 5) 1) (x – 5) 2) 105 k © copywriter 35