AngularMomentum Theory M Auzinsh D Budker S Rochester

Angular-Momentum Theory M. Auzinsh D. Budker S. Rochester Optically polarized atoms: understanding light -atom interactions Ch. 3

Rotations Classical rotations Commutation relations Quantum rotations Finding U (R ) D – functions Visualization Irreducible tensors Polarization moments 2

Classical rotations Rotations use a 3 x 3 matrix R: position or other vector Rotation by angle θ about z axis: For θ=π/2: For small angles: For arbitrary axis: Ji are “generators of infinitesimal rotations” 3

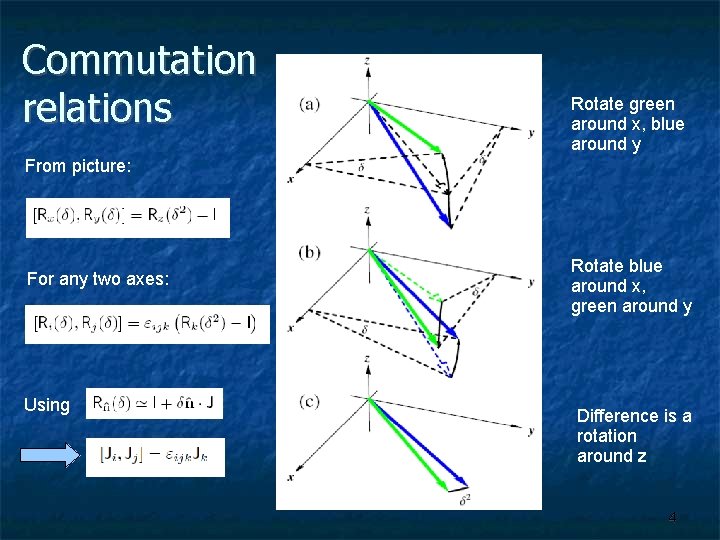
Commutation relations Rotate green around x, blue around y From picture: For any two axes: Using Rotate blue around x, green around y Difference is a rotation around z 4

Quantum rotations Want to find U (R) that corresponds to R U(R) should be unitary, and should rotate various objects as we expect E. g. , expectation value of vector operator: Remember, for spin ½, U is a 2 x 2 matrix A is a 3 -vector of 2 x 2 matrices R is a 3 x 3 matrix 5

Quantum rotations Infinitesimal rotations Like classical formula, except i makes J Hermitian For small θ: minus sign is conventional gives J units of angular momentum The Ji are the generators of infinitesimal rotations They are the QM angular momentum operators. This is the most general definition for J We can recover arbitrary rotation: 6

Quantum rotations Determining U (R) Start by demanding that U(R) satisfies same commutation relations as R The commutation relations specify J, and thus U(R) That's it! E. g. , for spin ½: 7

Quantum rotations Is it right? We've specified U(R), but does it do what we want? Want to check J is an observable, so check Do easy case: infinitesimal rotation around z Neglect δ 2 term Same Rz matrix as before 8

D -functions Matrix elements of the rotation operator Rotations do not change j. D-function z-rotations are simple: so we use Euler angles (z-y-z): 9