Angular momentum transport and mixing in rotating stars

Angular momentum transport and mixing in rotating stars Jean-Paul Zahn Observatoire de Paris Second Corot-Brazil Workshop Ubatuba, 2 -6 November 2005

Why bother about rotation in stars? • Rotation is the main cause of mixing in stellar radiation zones • It plays a major role in the generation and decay of magnetic field • Rotation intervenes in the mass loss hence its impact on stellar and galactic evolution

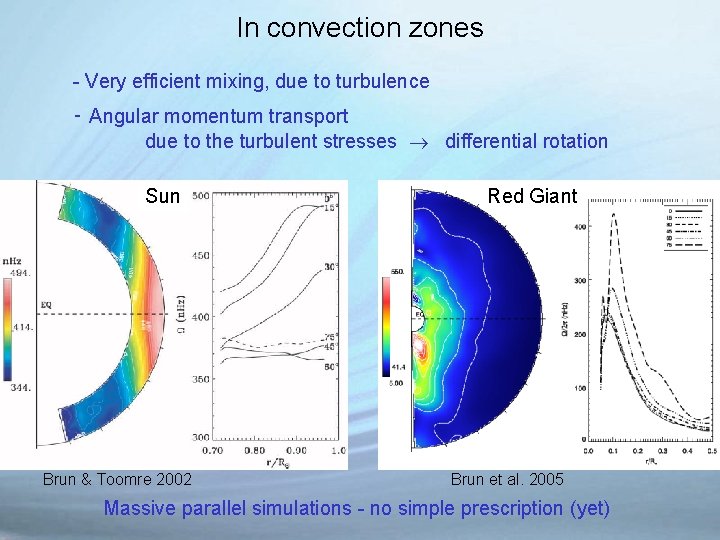
In convection zones - Very efficient mixing, due to turbulence - Angular momentum transport due to the turbulent stresses differential rotation Sun Brun & Toomre 2002 Red Giant Brun et al. 2005 Massive parallel simulations - no simple prescription (yet)

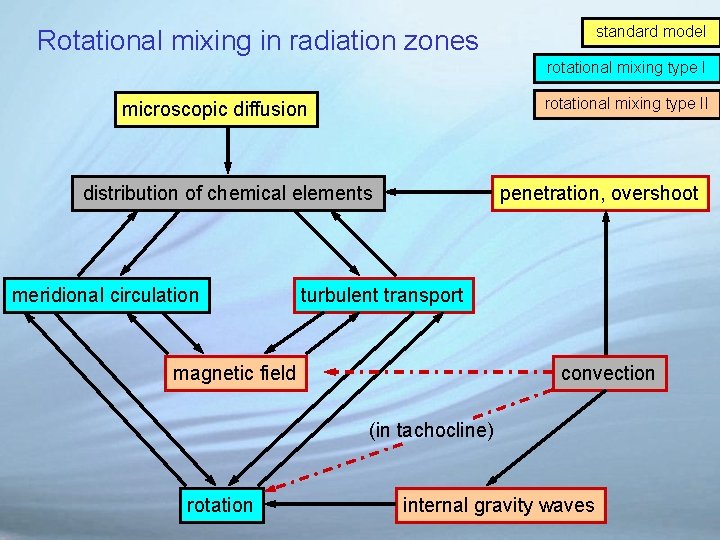
Mixing processes in radiation zones Main cause : (differential) rotation - Rotational mixing of type I Matter and angular momentum are transported by the same processes : meridional circulation and turbulence - Rotational mixing of type II Mixing is caused by circulation and turbulence, but another process (magnetic field, waves) intervenes in the transport of angular momentum

Mixing processes in radiation zones: rotational mixing of type I • Meridional circulation Classical picture: circulation is due to thermal imbalance caused by perturbing force (centrifugal, etc. ) Eddington (1925), Vogt (1925), Sweet (1950), etc Eddington-Sweet time Revised picture: after a transient phase of about t. ES, circulation is driven by the loss (or gain) of angular momentum Busse (1981), JPZ (1992), Maeder & Z (1998) No AM loss: no need to transport AM weak circulation AM loss by wind: need to transport AM to surface strong circulation

Turbulence caused by differential rotation By vertical shear W(r) (baroclinic instability) - if maximum of vorticity: linear instability - if no maximum of vorticity: finite amplitude instability - stabilizing effect of stratification reduced by radiative diffusion Richardson criterion turbulence if from which one deduces the turbulent diffusivity (if = cst) Townsend 1959 Dudis 1974; JPZ 1974 Lignières et al. 1999 K thermal diffusion; n viscosity; N buoyancy frequency

Turbulence caused by differential rotation By horizontal shear W( ) (barotropic instability) Assumptions: - instability acts to suppress its cause, i. e. W( ) - turbulent transport is anisotropic (due to stratification): Dh Dv Main weakness: no firm prescription for Dh Maeder 2003 Mathis, Palacios & Z 2004 2 important properties: - erodes stabilising effect of stratification Talon & Z 1997 - changes advection of chemicals into vertical diffusion Chaboyer & Z 1992

Rotational mixing of type I - the observational test The same processes (circulation and turbulence) responsible for the mixing of chemical elements and for the transport of angular momentum are Zahn (1992), Maeder & Zahn (1998) Quite successful with early-type stars Talon et al. 1997; Maeder & Meynet 2000; Talon & Charbonnel 1999 For late-type stars, predicts - fast rotating core helioseismology

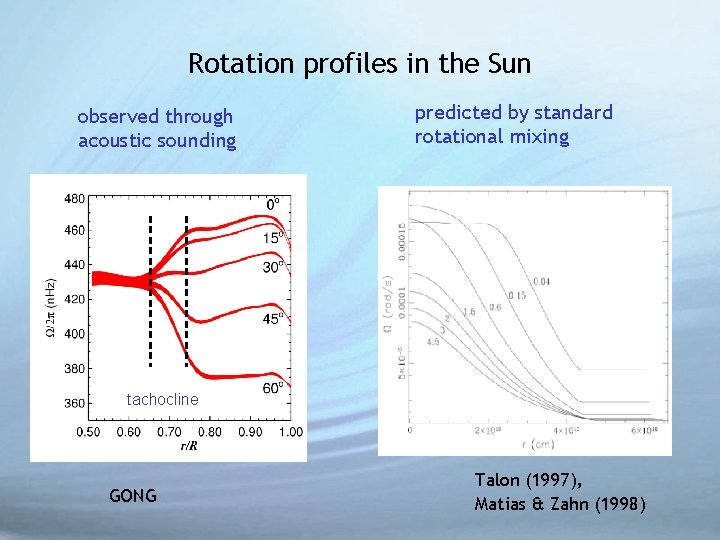
Rotation profiles in the Sun observed through acoustic sounding predicted by standard rotational mixing tachocline GONG Talon (1997), Matias & Zahn (1998)

Rotational mixing of type I - the observational test The same processes (circulation and turbulence) responsible for the mixing of chemical elements and for the transport of angular momentum are Zahn (1992), Maeder & Zahn (1998) Quite successful with early-type stars Talon et al. 1997; Maeder & Meynet 2000; Talon & Charbonnel 1999 · For late-type stars, predicts - fast rotating core helioseismology - strong destruction of Be in Sun (may be explained by tachocline mixing) - mixing correlated with loss of angular momentum Li in tidally locked binaries little dispersion in the Spite plateau Another, more powerful process is responsible for the transport of angular momentum

Rotational mixing of type II Circulation and turbulence are responsible for the mixing of chemical elements Another process operates for the transport of angular momentum; has indirect impact on mixing, by shaping the rotation profile · Magnetic field ? · Internal gravity waves ?

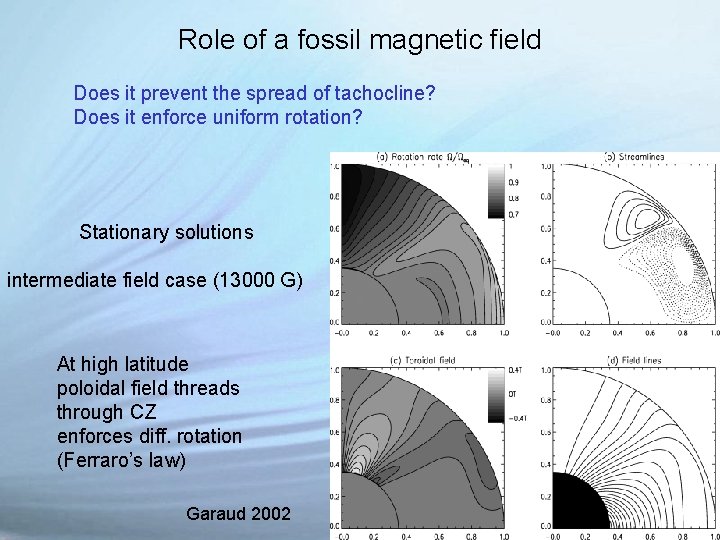
Role of a fosssil magnetic field Does it prevent the spread of tachocline? Does it enforce uniform rotation? convection zone tachocline void of magnetic field magnetopause Gough & Mc. Intyre 1998

Role of a fossil magnetic field Does it prevent the spread of tachocline? Does it enforce uniform rotation? Stationary solutions intermediate field case (13000 G) At high latitude poloidal field threads through CZ enforces diff. rotation (Ferraro’s law) Garaud 2002

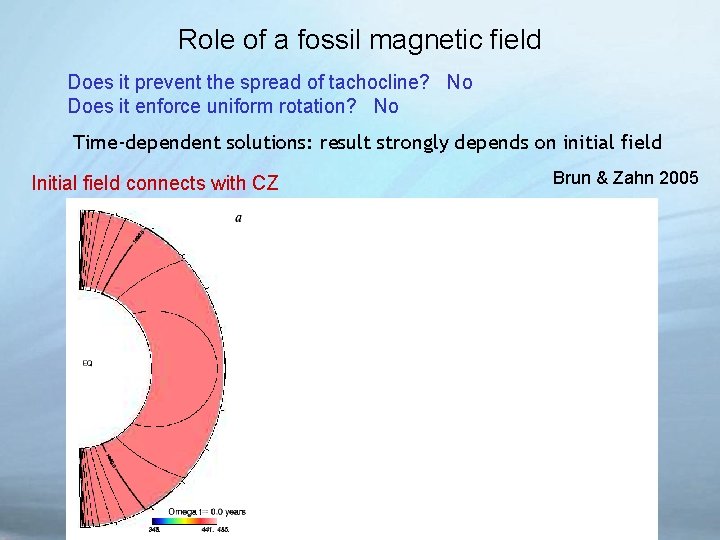
Role of a fossil magnetic field Does it prevent the spread of tachocline? No Does it enforce uniform rotation? No Time-dependent solutions: result strongly depends on initial field Initial field connects with CZ Brun & Zahn 2005

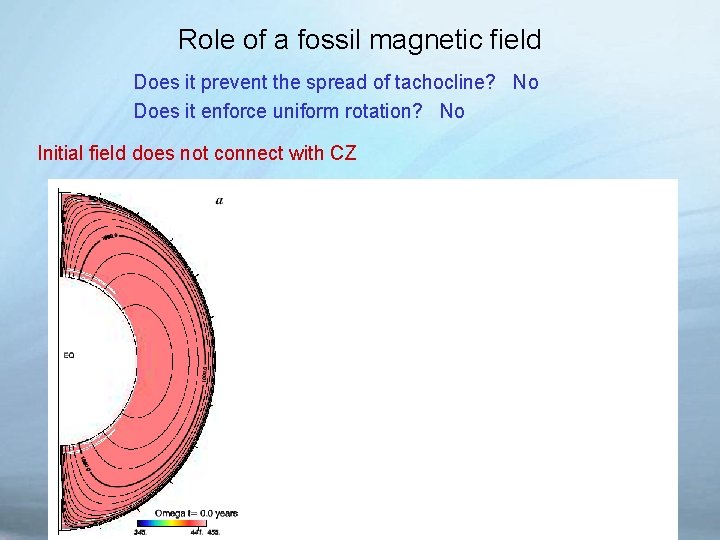
Role of a fossil magnetic field Does it prevent the spread of tachocline? No Does it enforce uniform rotation? No Initial field does not connect with CZ

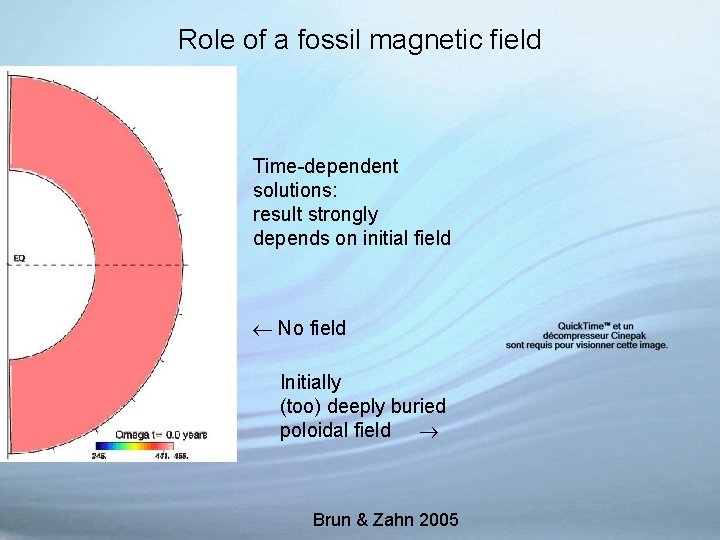
Role of a fossil magnetic field Time-dependent solutions: result strongly depends on initial field No field Initially (too) deeply buried poloidal field Brun & Zahn 2005

Role of a fossil magnetic field Time-dependent solutions: result strongly depends on initial field No field Initially (too) deeply buried poloidal field Brun & Zahn 2005

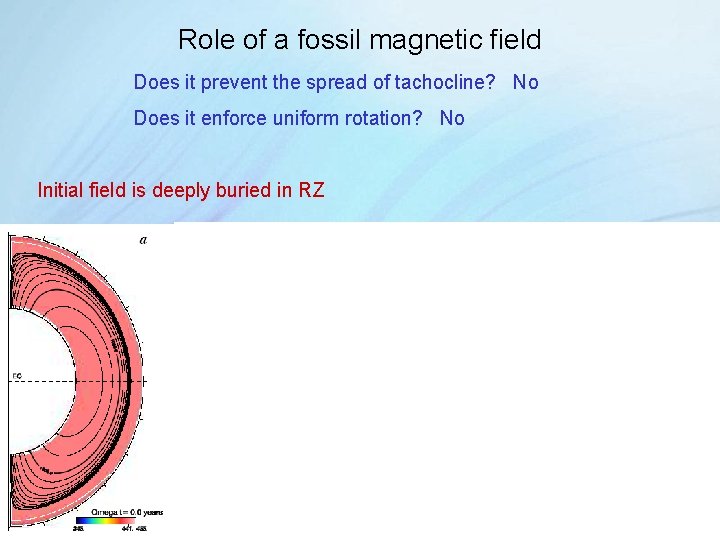
Role of a fossil magnetic field Does it prevent the spread of tachocline? No Does it enforce uniform rotation? No Initial field is deeply buried in RZ

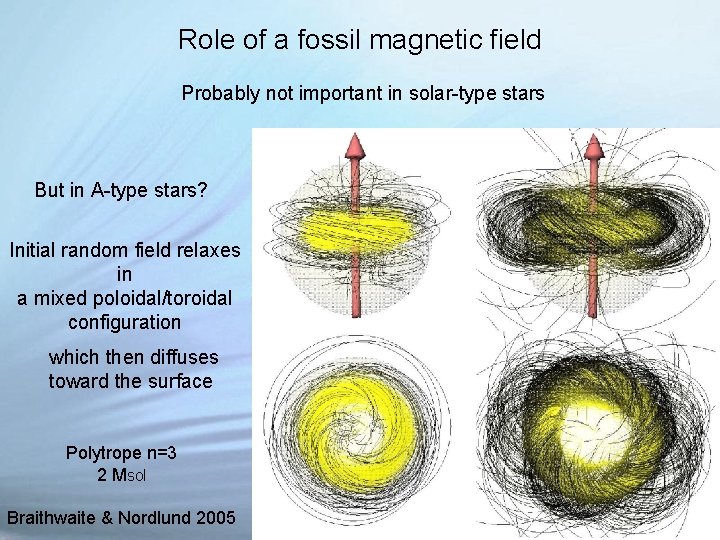
Role of a fossil magnetic field Probably not important in solar-type stars But in A-type stars? Initial random field relaxes in a mixed poloidal/toroidal configuration which then diffuses toward the surface Polytrope n=3 2 Msol Braithwaite & Nordlund 2005

Properties of internal gravity waves • Propagate in stratified media • restoring force buoyancy (Brunt-Väisälä) frequency oscillation frequency of a displaced element in a stratified region • Excited by turbulence (e. g. in or close to convective zones) • Conserve momentum (or angular momentum) – if they are not damped transport AM to place where they are dissipated

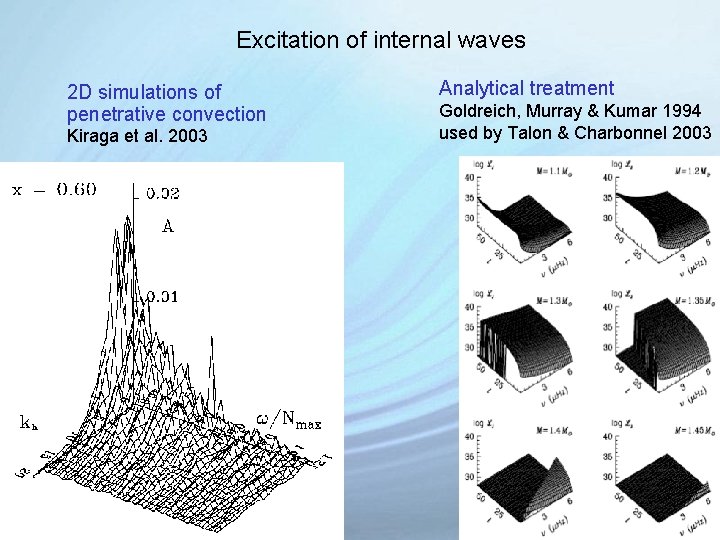
Excitation of internal waves 2 D simulations of penetrative convection Kiraga et al. 2003 Analytical treatment Goldreich, Murray & Kumar 1994 used by Talon & Charbonnel 2003

Momentum transport by waves • In stars, IGW are damped by thermal diffusion flux at the base of the CZ frequency in frame rotating with CZ thermal diffusion local frequency is Doppler shifted if there is differential rotation Waves transfer momentum from the region where they are excited to the region where they are dissipated

Momentum transport by waves - if prograde (m>0) and retrograde (m<0) waves are equally excited and if there is no differential rotation no net momentum deposition - if there is differential rotation, +m and -m waves deposit their momentum at different locations waves increase the local differential rotation · high l waves are damped very close to the CZ

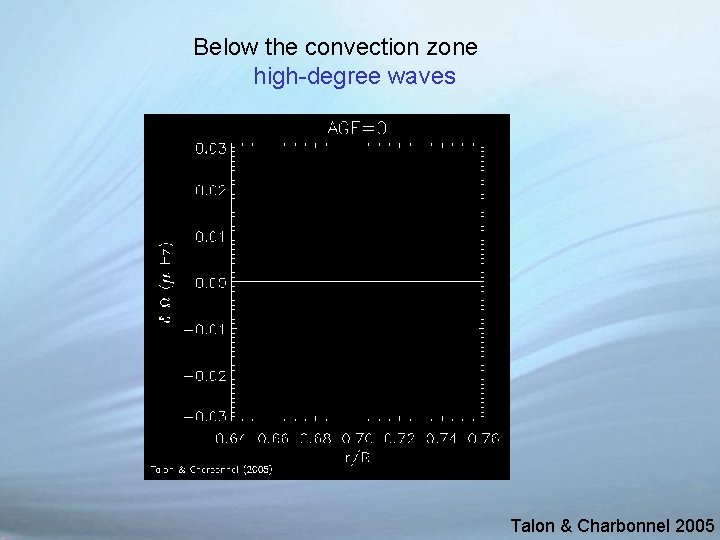
Below the convection zone high-degree waves Talon & Charbonnel 2005

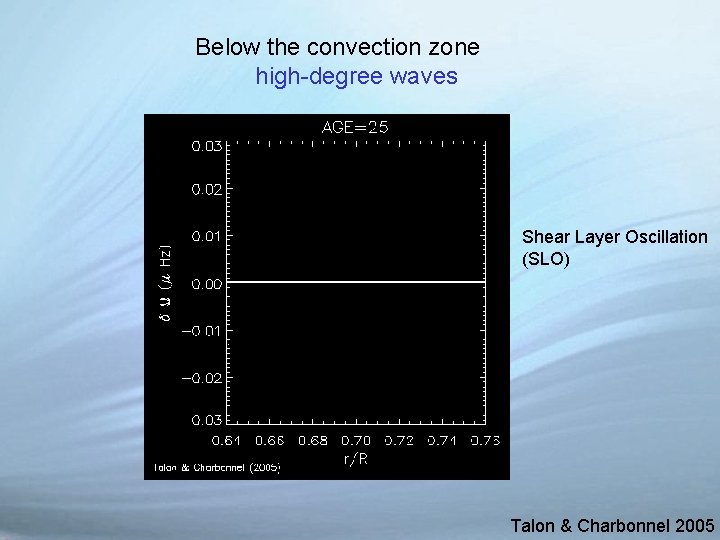
Below the convection zone high-degree waves Shear Layer Oscillation (SLO) Talon & Charbonnel 2005

Momentum transport by waves • if prograde (m>0) and retrograde (m<0) waves are equally excited and there is no differential rotation no net momentum deposition • if there is differential rotation, +m and -m waves deposit their momentum at different locations waves increase the local differential rotation - high l waves are damped very close to the CZ - low l, low frequency waves are damped in deep interior

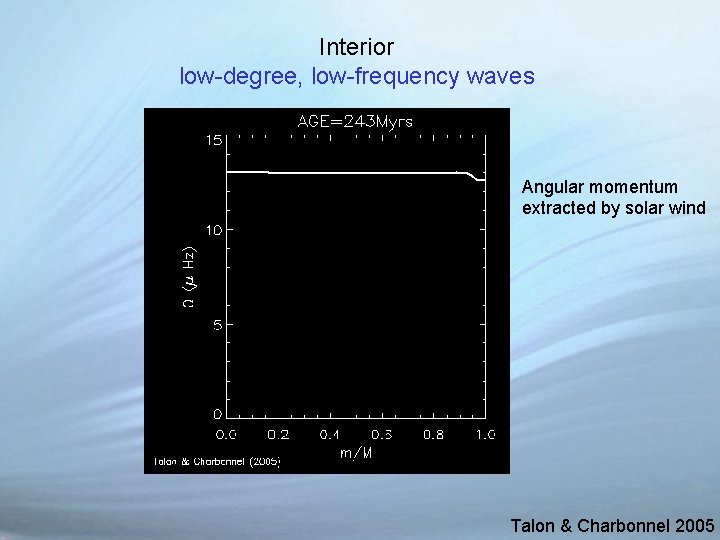
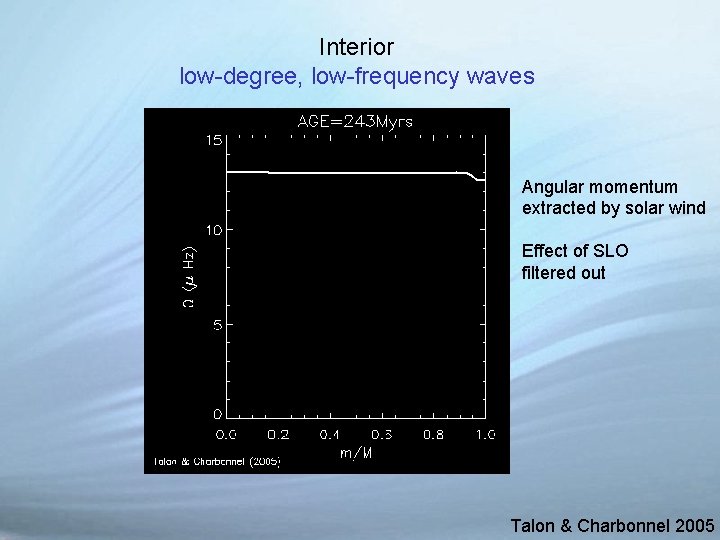
Interior low-degree, low-frequency waves Angular momentum extracted by solar wind Talon & Charbonnel 2005

Interior low-degree, low-frequency waves Angular momentum extracted by solar wind Effect of SLO filtered out Talon & Charbonnel 2005

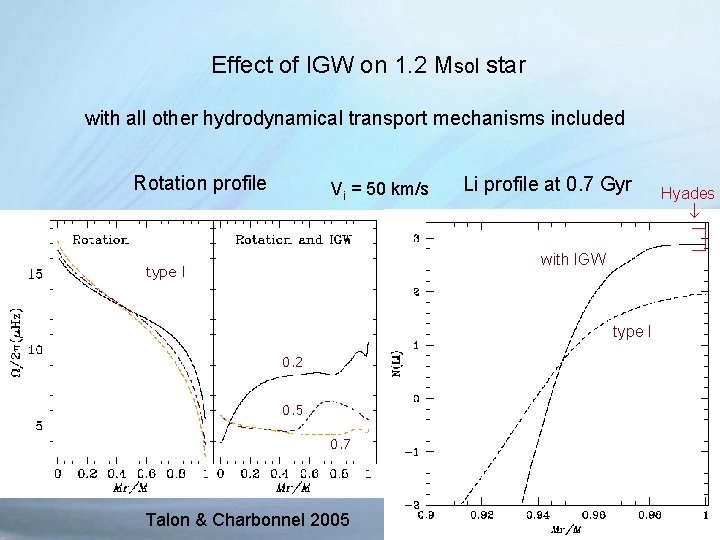
Effect of IGW on 1. 2 Msol star with all other hydrodynamical transport mechanisms included Rotation profile Vi = 50 km/s Li profile at 0. 7 Gyr with IGW type I 0. 2 0. 5 0. 7 Talon & Charbonnel 2005 Hyades

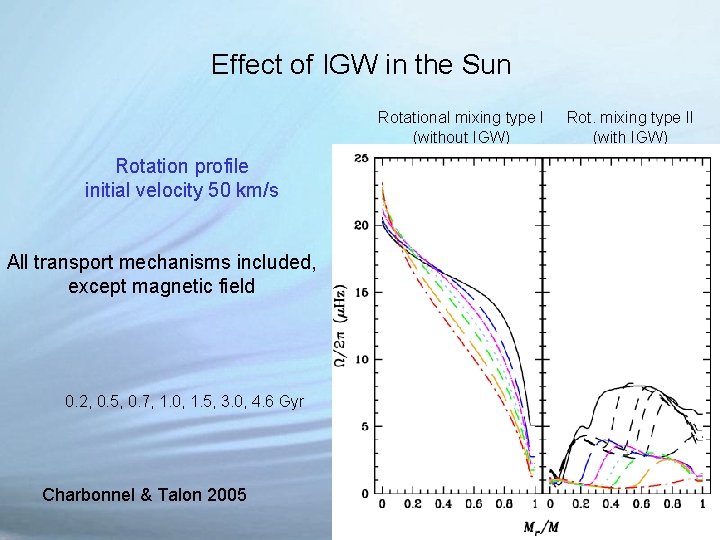
Effect of IGW in the Sun Rotational mixing type I (without IGW) Rotation profile initial velocity 50 km/s All transport mechanisms included, except magnetic field 0. 2, 0. 5, 0. 7, 1. 0, 1. 5, 3. 0, 4. 6 Gyr Charbonnel & Talon 2005 Rot. mixing type II (with IGW)

standard model Rotational mixing in radiation zones rotational mixing type II microscopic diffusion distribution of chemical elements meridional circulation penetration, overshoot turbulent transport magnetic field convection (in tachocline) rotation internal gravity waves

Weakest points of present models - Convective penetration into radiation zones - Parametrisation of shear turbulence due to differential rotation - Power spectrum for IGW emitted at base of convection zone - Particle transport by IGW ? - Role of magnetic field ? Co. Ro. T will put most valuable constraints