Angular Momentum Projection in TDHF Dynamics application to

Angular Momentum Projection in TDHF Dynamics : application to Coulomb excitation and fusion C. Simenel 1, 2 In collaboration with M. Bender 2, T. Duguet 2, F. Nunes 2 1) CEA-SPh. N, Saclay 2) MSU/NSCL, US

Motivations Nuclear reactions • elastic, inelastic, deep-inelastic, transfer, break-up, fusion, fission… • Coulomb + nuclear interactions, couplings, multistep process, tunnel effect… Whole nuclear chart • from light to superheavy elements • from proton to neutron drip lines Fully microscopic theory effective interaction (Skyrme, Gogny…) Beyond mean-field • long range dynamical correlations • mixing of trajectories

Present status Time dependent mean field • Time-Dependent Hatree-Fock theory P. A. M. Dirac, Proc. Camb. Phil. Soc. 26, 376 (1930) • First application to nuclear physics Y. M. Engel et al. , NPA 249, 215 (1975) P. Bonche, S. Koonin and J. W. Negele, PRC 13, 1226 (1976) • 3 D calculations of nuclear reactions H. Flocard, S. E. Koonin and M. S. Weiss, PRC 17, 1682 (1978) K. -H. Kim, T. Otsuka and P. Bonche, JPG 23, 1267 (1997) C. S. , P. Chomaz and G. de France, PRL 86, 2971 (2001) C. S. , P. Chomaz and G. de France, PRL 93, 102701 (2004) • no pairing (except QRPA)

Present status Beyond time dependent mean field • Extended TDHF D. Lacroix, P. Chomaz and S. Ayik, PRC 58, 2154 (1998) • Time Dependent Density Matrix S. J. Wang and W. Cassing, Ann. Phys. 159, 328 (1985) M. Tohyama, PRC 36, 187 (1987) • Stochastic TDHF O. Juillet and P. Chomaz, PRL 88, 142503 (1998) • Time Dependent Generator Coordinate Method P. -G. Reinhard, R. Y. Cusson and K. Goeke, NPA 398, 141 (1983) J. F. Berger, M. Girod and D. Gogny, NPA 428, 23 c (1984) H. Goutte, J. F. Berger, P. Casoli and D. Gogny, PRC 71, 024316 (2005) • Projected TDHF (present work)

Today's objectives: reactions with a deformed projectile effect of the initial orientation on the reaction many TDHF trajectories Coulomb excitation (rotation) • angular momentum projection to calculate the J-population • Interferences between initial orientations Fusion • incoherent mixing of TDHF trajectories realistic fusion probability (between 0 and 1) • Effect of Coulomb excitation in the approach

I) Projected TDHF : formalism A) Projection on angular momentum • static case angular momentum "projector": rotated Slater determinant: • evolution no feed back of the correlations - on the Slater evolution TDHF trajectories - on the superposition functions f( ) is constant initial state correlations in the observation only

I) Projected TDHF : formalism B) Projection on angular momentum • exact J-population we use high computationnal cost • approximated J-population accurate if the vibration and the rotational speed are small

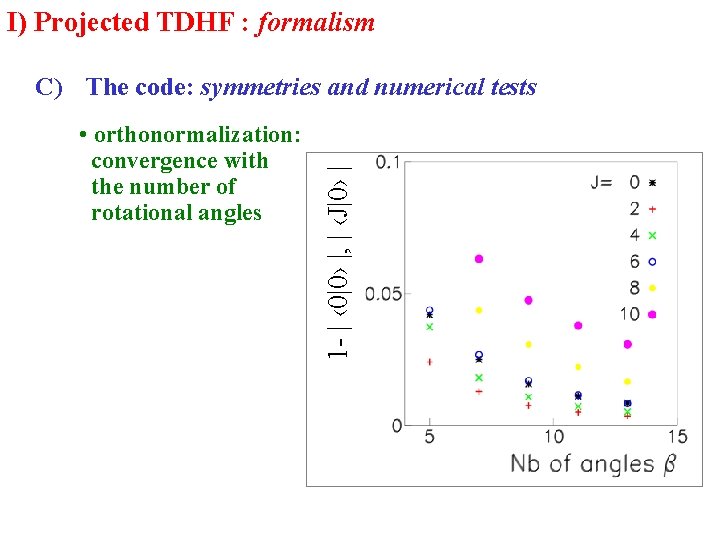
I) Projected TDHF : formalism C) The code: symmetries and numerical tests • initial condition: isotropic distribution of (J=0) • axial symmetry of small impact parameter or small dynamical deformation of (t) or sudden approximation • the HF g. s. has an axial symmetry, a time-reversal symmetry and a good parity • the evolved Slater determinants symmetry only one collision partner can be deformed • no charge mixing in the s. p. wave functions have a plane of

I) Projected TDHF : formalism C) The code: symmetries and numerical tests • explicit expression of the JM-population - exact with and - approximated

I) Projected TDHF : formalism • orthonormalization: convergence with the number of rotational angles 1 - | ‹ 0|0› |, | ‹J|0› | C) The code: symmetries and numerical tests

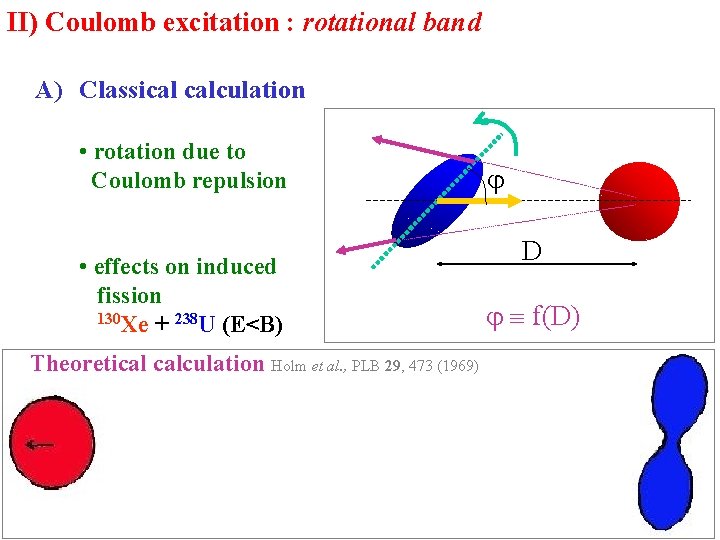
II) Coulomb excitation : rotational band A) Classical calculation • rotation due to Coulomb repulsion • effects on induced fission 130 Xe + 238 U (E<B) Theoretical calculation Holm et al. , PLB 29, 473 (1969) D f(D)

II) Coulomb excitation : rotational band A) Classical calculation K. Alder and A. Winther, Electromagnetic Excitation (1978) C. S. , P. Chomaz and G. de France, PRL 93, 102701 (2004) Z 1, A 1 - point like target - small D - small - differential equation : with and - solution : - reorientation ( =1) : Z 2, A 2

II) Coulomb excitation : rotational band B) TDHF approach • self consistent mean field theory • independant s. p. wave functions • mean values of one body observables (ex : orientation) • quantal treatment of inertia • P. Bonche code K. -H. Kim, T. Otsuka and P. Bonche, JPG 23, 1267 (1997) deformed projectile + Coulomb potential of the target • Skyrme forces (SLy 4 d) T. Skyrme, Phil. Mag. 1 (1956)

II) Coulomb excitation : rotational band B) TDHF approach • 24 Mg (+ 208 Pb) • ECM = 112 Me. V (≈B) • Dinit. = 220 fm • head on collision` • Rutherford trajectory • approach phase only

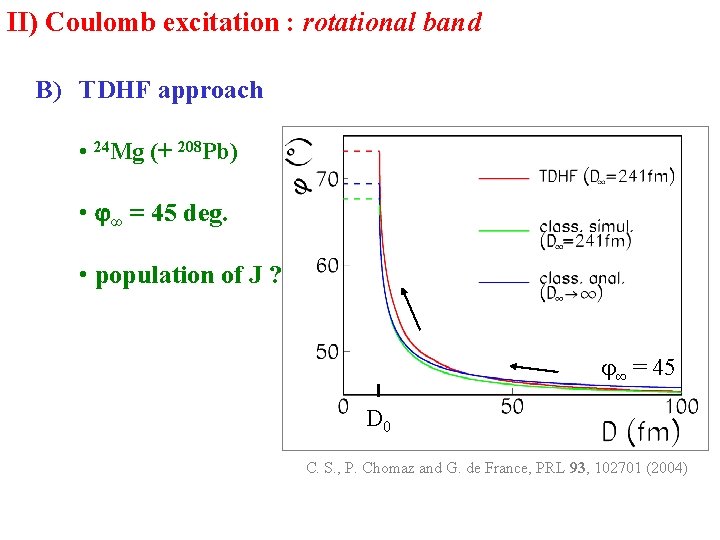
II) Coulomb excitation : rotational band B) TDHF approach • 24 Mg (+ 208 Pb) • ∞ = 45 deg. • population of J ? ∞ = 45 D 0 C. S. , P. Chomaz and G. de France, PRL 93, 102701 (2004)

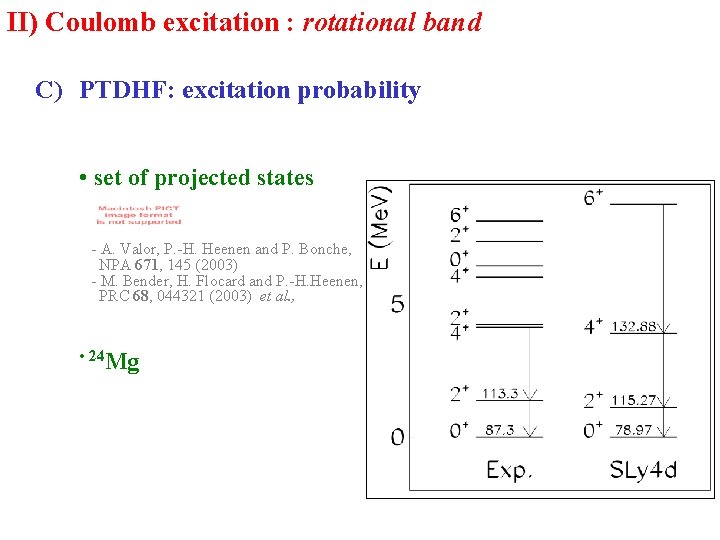
II) Coulomb excitation : rotational band C) PTDHF: excitation probability • set of projected states - A. Valor, P. -H. Heenen and P. Bonche, NPA 671, 145 (2003) - M. Bender, H. Flocard and P. -H. Heenen, PRC 68, 044321 (2003) et al. , • 24 Mg

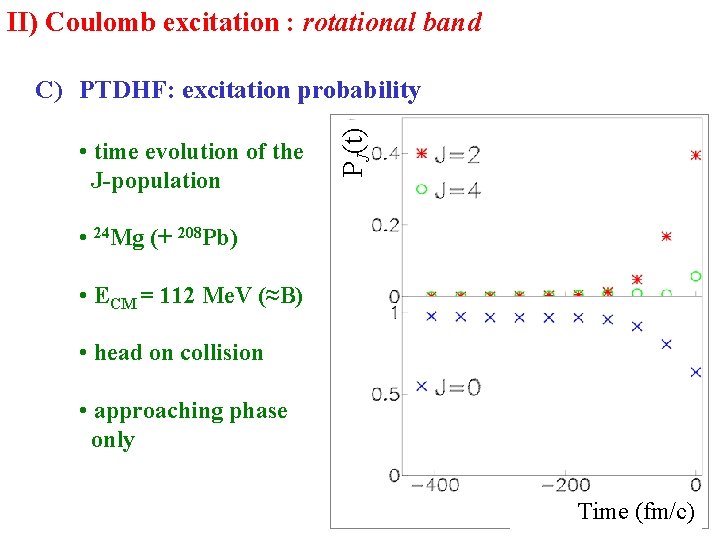
II) Coulomb excitation : rotational band • time evolution of the J-population PJ(t) C) PTDHF: excitation probability • 24 Mg (+ 208 Pb) • ECM = 112 Me. V (≈B) • head on collision • approaching phase only Time (fm/c)

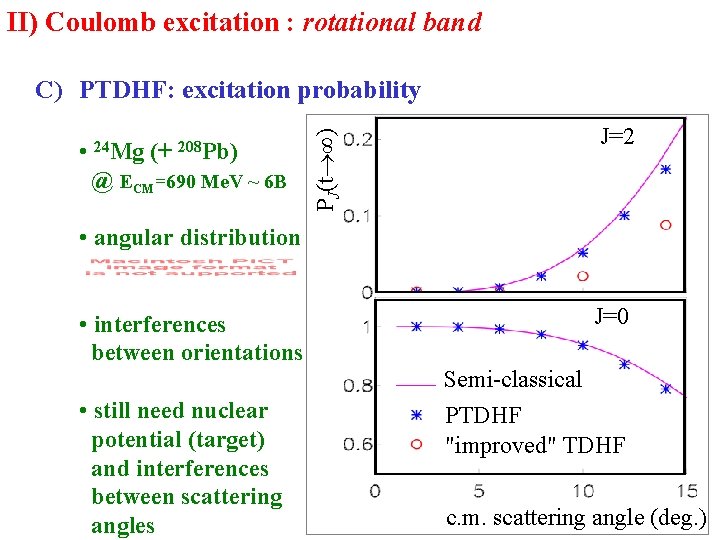
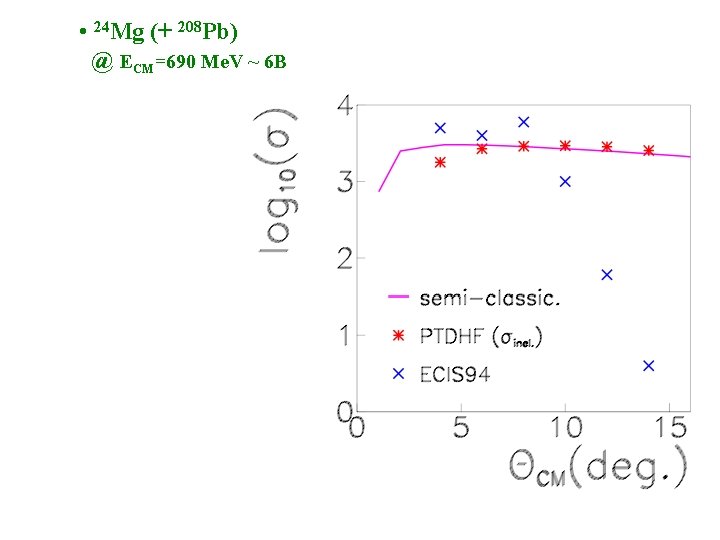
II) Coulomb excitation : rotational band • 24 Mg (+ 208 Pb) @ ECM=690 Me. V ~ 6 B PJ(t ∞) C) PTDHF: excitation probability J=2 • angular distribution • interferences between orientations • still need nuclear potential (target) and interferences between scattering angles J=0 Semi-classical PTDHF "improved" TDHF c. m. scattering angle (deg. )

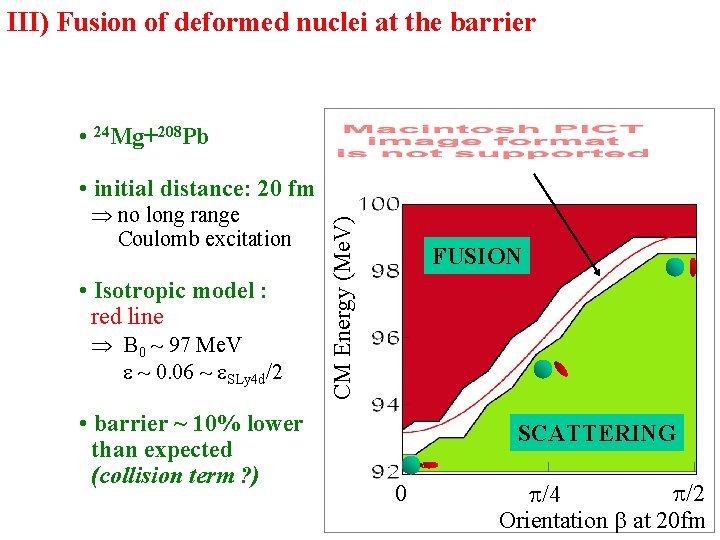
III) Fusion of deformed nuclei at the barrier • 24 Mg+208 Pb @ 94 Me. V • head-on collision • initial distance: 20 fm • the fusion probability depends on the initial orientation

III) Fusion of deformed nuclei at the barrier • 24 Mg+208 Pb no long range Coulomb excitation • Isotropic model : red line B 0 ~ 97 Me. V ~ 0. 06 ~ SLy 4 d/2 • barrier ~ 10% lower than expected (collision term ? ) CM Energy (Me. V) • initial distance: 20 fm FUSION SCATTERING 0 /2 /4 Orientation at 20 fm

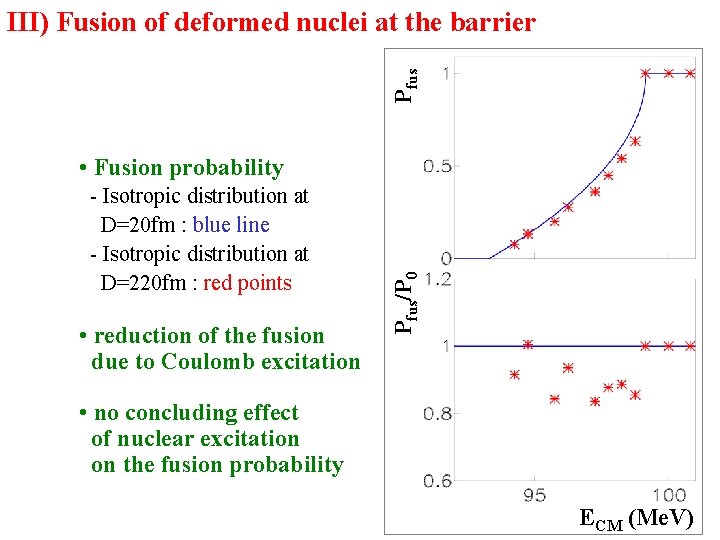
Pfus III) Fusion of deformed nuclei at the barrier - Isotropic distribution at D=20 fm : blue line - Isotropic distribution at D=220 fm : red points • reduction of the fusion due to Coulomb excitation Pfus/P 0 • Fusion probability • no concluding effect of nuclear excitation on the fusion probability ECM (Me. V)

Conclusions and perspectives PTDHF • approximated angular momentum projection on TDHF trajectories • beyond mean field for the observation, ex: PJ(t) • Coulomb excitation strong effect of the interferences • fusion reduction of the fusion due to Coulomb excitation exact projection interferences between scattering angles effect of interferences (orientations) on fusion ? feed back of the correlations on the evolution TDGCM pairing (TDHF)

annexe

Plan I) Projected TDHF: Formalism • Time Dependent Generator Coordinate Method • Projection on angular momentum • The code: symmetries and numerical tests II) Coulomb excitation: 24 Mg rotationnal band • Classical calculation • TDHF approach • PTDHF: excitation probability III) Fusion of deformed nuclei at the barrier • Rotationnal couplings in the entrance channel • Beyond mean field results IV) Conclusions and perspectives

I) Projected TDHF : formalism A) TDGCM • wave function q: collective variable f : superposition function : Slater determinant P. -G. Reinhard et al. (t) TDHF(t) J. F. Berger et al. + H. Goutte et al. (t) HFB • time dependent Griffin-Hill-Wheeler equation

I) Projected TDHF : formalism C) The code: symmetries and numerical tests • explicit expression of the JM-population - exact with and - approximated - without interferences

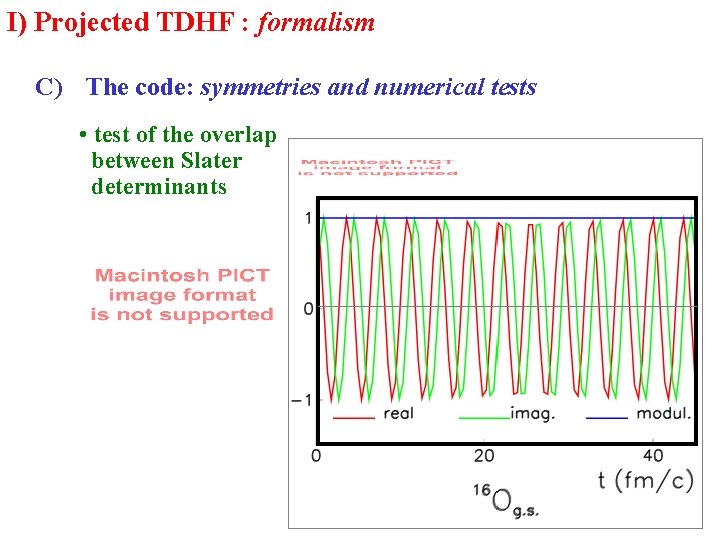
I) Projected TDHF : formalism C) The code: symmetries and numerical tests • test of the overlap between Slater determinants

• 24 Mg (+ 208 Pb) @ ECM=690 Me. V ~ 6 B