Angular Mechanics Torque and moment of inertia Contents








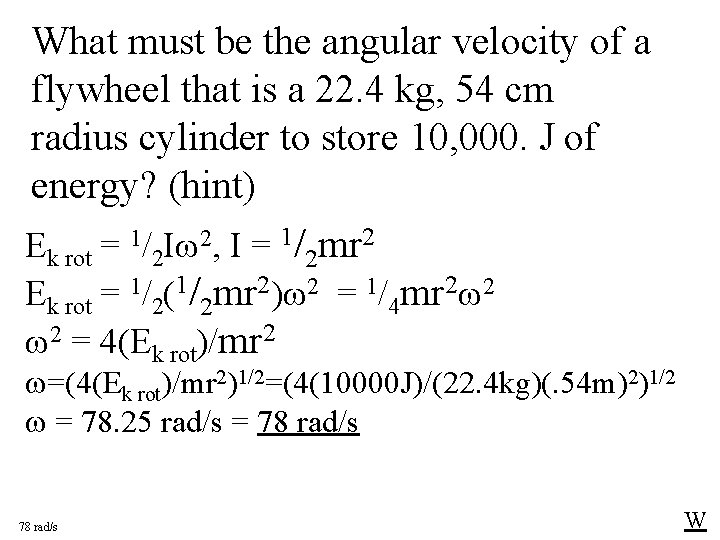



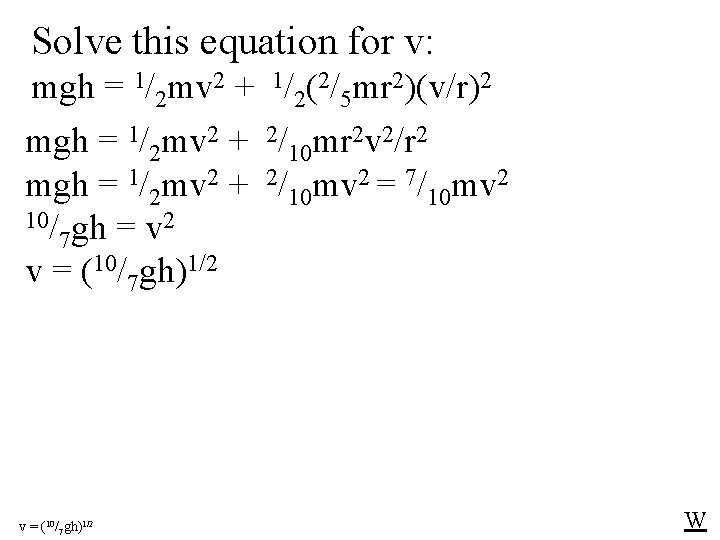




- Slides: 21

Angular Mechanics - Torque and moment of inertia Contents: • Review • Linear and angular Qtys • Tangential Relationships • Angular Kinematics • Rotational KE • Example | Whiteboard • Rolling Problems • Example | Whiteboard

Angular Mechanics - Angular Quantities Linear: Angular: (m) s - Angle (Radians) (m/s) u o - Initial angular velocity (Rad/s) (m/s) v - Final angular velocity (Rad/s) (m/s/s) a - Angular acceleration (Rad/s/s) (s) t t - Uh, time (s) (N) F - Torque (kg) m I - Moment of inertia TOC

Angular Mechanics - Angular kinematics Linear: s/ t = v v/ t = a u + at = v ut + 1/2 at 2 = s u 2 + 2 as = v 2 (u + v)t/2 = s ma = F 1/ mv 2 = E 2 kin Fs = W Angular: = / t* = o + t = ot + 1/2 t 2 2 = o 2 + 2 = ( o + )t/2* = I Ek rot = 1/2 I 2 W = * *Not in data packet TOC

Angular Mechanics - Useful Substitutions = I = r. F so F = /r = I /r s = r, so = s/r v = r, so = v/r a = r, so = a/r TOC

Angular Mechanics - Rotational Ke Two types of kinetic energy: Translational: Ekin = 1/2 mv 2 Rotational: Ek rot = 1/2 I 2 Of course a rolling object has both IP Demo Rolling. ip TOC

Example: What Energy does it take to speed up a 23. 7 kg 45 cm radius cylinder from rest to 1200 RPM? TOC

Whiteboards: Rotational KE 1|2|3 TOC

What is the rotational kinetic energy of an object with an angular velocity of 12 rad/s, and a moment of inertia of 56 kgm 2? Ek rot = 1/2 I 2 Ek rot = 1/2(56 kgm 2)(12 rad/s)2 Ek rot = 4032 J = 4. 0 x 103 J W
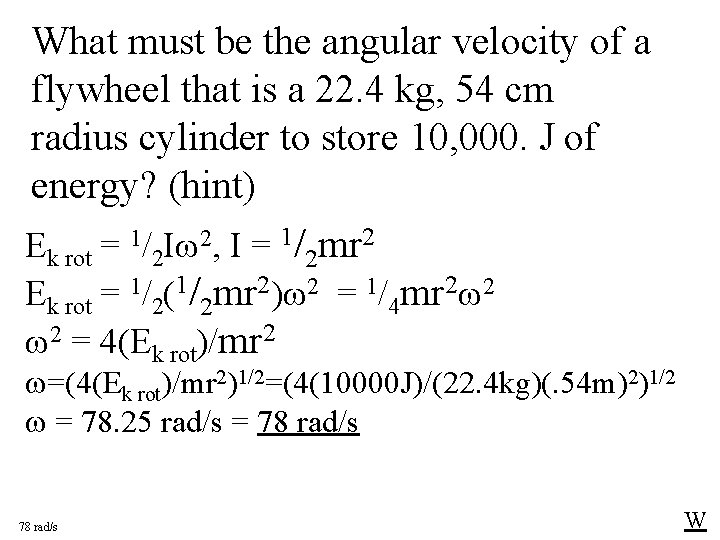
What must be the angular velocity of a flywheel that is a 22. 4 kg, 54 cm radius cylinder to store 10, 000. J of energy? (hint) Ek rot = 1/2 I 2, I = 1/2 mr 2 Ek rot = 1/2(1/2 mr 2) 2 = 1/4 mr 2 2 2 = 4(Ek rot)/mr 2 =(4(Ek rot)/mr 2)1/2=(4(10000 J)/(22. 4 kg)(. 54 m)2)1/2 = 78. 25 rad/s = 78 rad/s W

What is the total kinetic energy of a 2. 5 cm diameter 405 g sphere rolling at 3. 5 m/s? (hint) I=2/5 mr 2, = v/r, Ek rot=1/2 I 2 , Ekin=1/2 mv 2 Ek total= 1/2 mv 2 +1/2 I 2 Ek total= 1/2 mv 2 +1/2(2/5 mr 2)(v/r)2 Ek total= 1/2 mv 2 +2/10 mv 2 = 7/10 mv 2 Ek total= 7/10 mv 2 = 7/10(. 405 kg)(3. 5 m/s)2 Ek total= 3. 473 J = 3. 5 J W

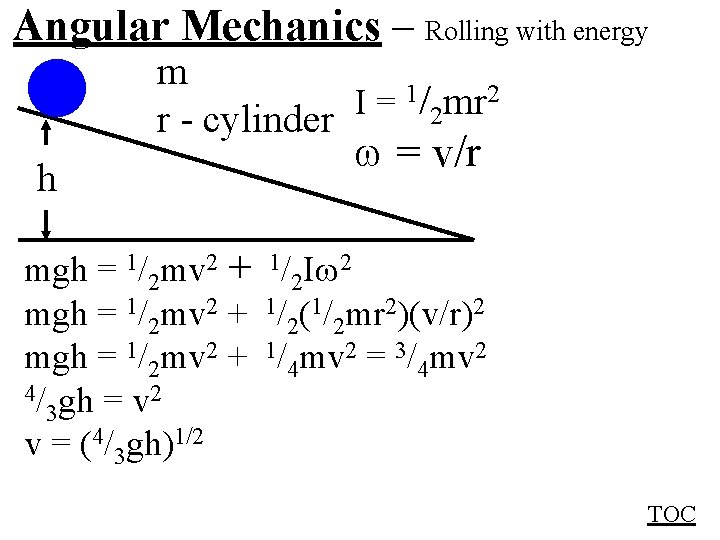
Angular Mechanics – Rolling with energy m 1/ mr 2 I = 2 r - cylinder h = v/r mgh = 1/2 mv 2 + 1/2 I 2 mgh = 1/2 mv 2 + 1/2(1/2 mr 2)(v/r)2 mgh = 1/2 mv 2 + 1/4 mv 2 = 3/4 mv 2 4/ gh = v 2 3 v = (4/3 gh)1/2 TOC

Whiteboards: Rolling with Energy 1|2|3 TOC

A 4. 5 kg ball with a radius of. 12 m rolls down a 2. 78 m long ramp that loses. 345 m of elevation. Set up the energy equation without plugging any of the knowns into it. Make substitutions for I and , but don’t simplify. I = 2/5 mr 2, = v/r mgh = 1/2 mv 2 + 1/2 I 2 mgh = 1/2 mv 2 + 1/2(2/5 mr 2)(v/r)2 W
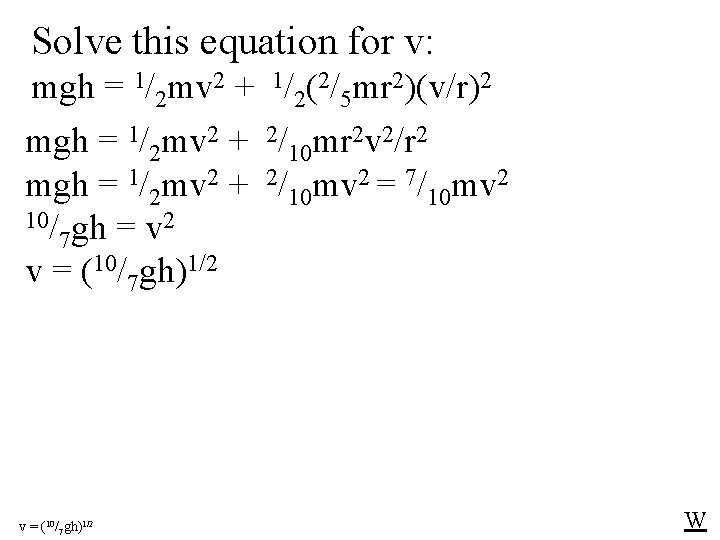
Solve this equation for v: mgh = 1/2 mv 2 + 1/2(2/5 mr 2)(v/r)2 mgh = 1/2 mv 2 + 2/10 mr 2 v 2/r 2 mgh = 1/2 mv 2 + 2/10 mv 2 = 7/10 mv 2 10/ gh = v 2 7 v = (10/7 gh)1/2 W

A 4. 5 kg ball with a radius of. 12 m rolls down a 2. 78 m long ramp that loses. 345 m of elevation. What is the ball’s velocity at the bottom? (v = (10/7 gh)1/2) v = (10/7(9. 8 m/s/s)(. 345 m))1/2 = 2. 1977 m/s v = 2. 20 m/s W

A 4. 5 kg ball with a radius of. 12 m rolls down a 2. 78 m long ramp that loses. 345 m of elevation. What was the rotational velocity of the ball at the bottom? (v = 2. 1977 m/s) = v/r = (2. 1977 m/s)/(. 12 m) = 18. 3 s-1 = 18 s-1 18 rad/s W

A 4. 5 kg ball with a radius of. 12 m rolls down a 2. 78 m long ramp that loses. 345 m of elevation. What was the linear acceleration of the ball down the ramp? (v = 2. 1977 m/s) v 2 = u 2 + 2 as v 2/(2 s) = a (2. 1977 m/s)2/(2(2. 78 m)) =. 869 m/s/s W

In General: I tend to solve all rotational dynamics problems using energy. 1. Set up the energy equation 2. (Make up a height) 3. Substitute linear for angular: • = v/r • I = ? mr 2 4. Solve for v 5. Go back and solve for accelerations TOC

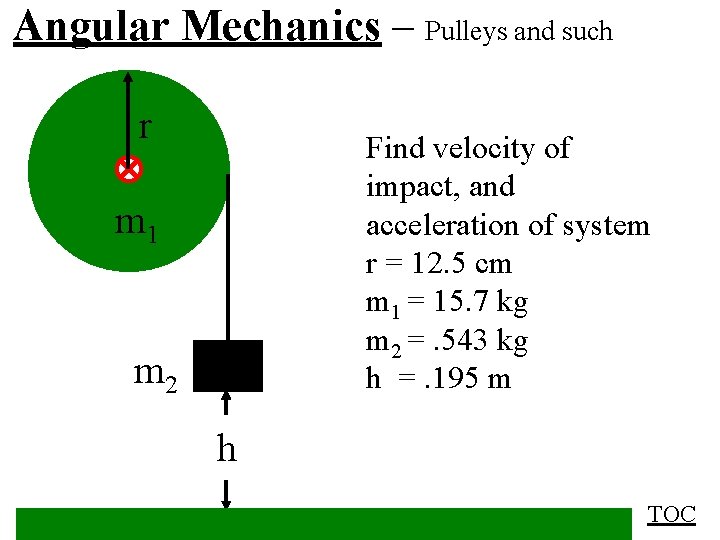
Angular Mechanics – Pulleys and such r Find velocity of impact, and acceleration of system r = 12. 5 cm m 1 = 15. 7 kg m 2 =. 543 kg h =. 195 m m 1 m 2 h TOC

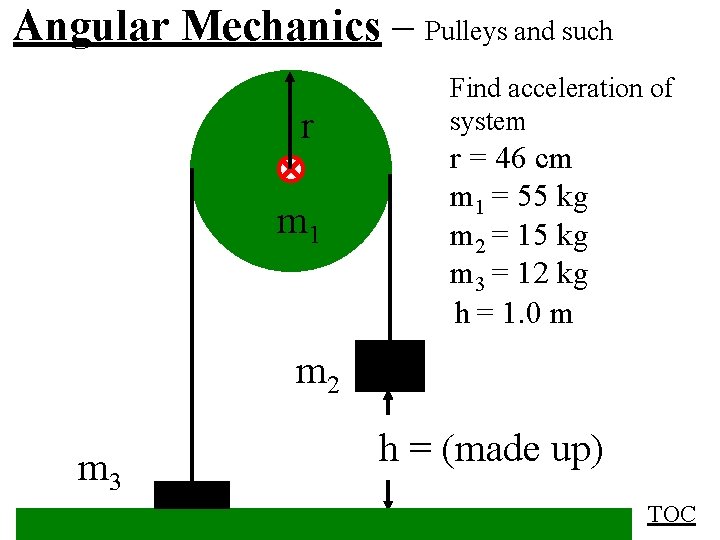
Angular Mechanics – Pulleys and such r m 1 Find acceleration of system r = 46 cm m 1 = 55 kg m 2 = 15 kg m 3 = 12 kg h = 1. 0 m m 2 m 3 h = (made up) TOC

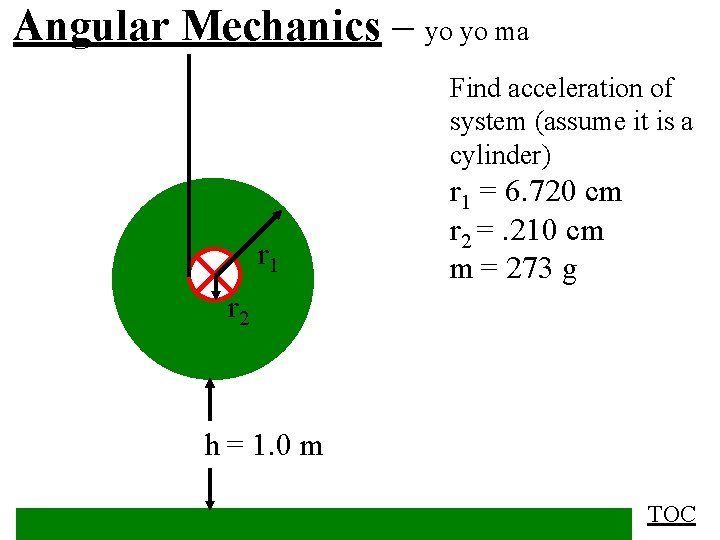
Angular Mechanics – yo yo ma Find acceleration of system (assume it is a cylinder) r 1 = 6. 720 cm r 2 =. 210 cm m = 273 g r 2 h = 1. 0 m TOC