Angular Kinematics Angular motion occurs when all points

Angular Kinematics Angular motion occurs when all points on an object move in circular paths about the same fixed axis. Chapter 6 in the text 3/10/2021 Dr. Sasho Mac. Kenzie - HK 376 1

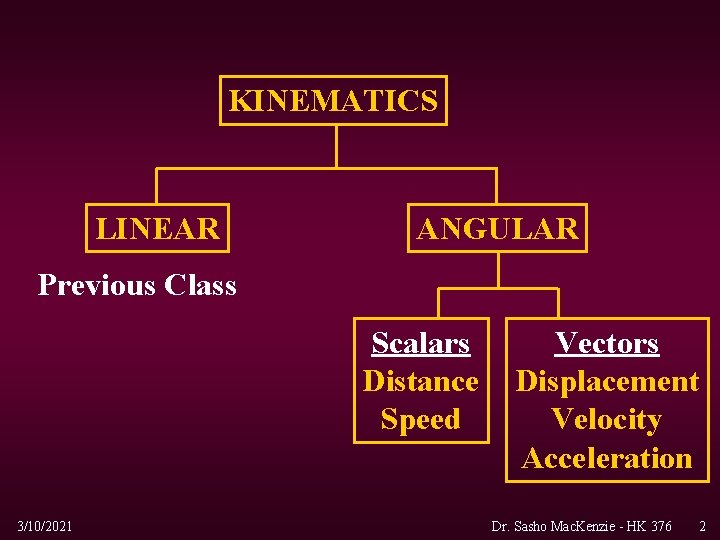
KINEMATICS LINEAR ANGULAR Previous Class Scalars Distance Speed 3/10/2021 Vectors Displacement Velocity Acceleration Dr. Sasho Mac. Kenzie - HK 376 2

What is an angle? • An angle is formed by the intersection of two lines. • The symbol for angle is (Theta). • Angles can be measured in degrees or radians (rads). 1 rad = 180/Pi = 57. 3 3/10/2021 Dr. Sasho Mac. Kenzie - HK 376 3

Angular Displacement Arc length Angular displacement (rads) radius Angular displacement is the change in angular position experienced by a rotating line. A vector quantity. 3/10/2021 Dr. Sasho Mac. Kenzie - HK 376 4

Direction of an angular vector • Not like linear vectors. Angular vectors are perpendicular to the plane of motion. • Must use right hand rule – Curl fingers of rt. hand in the direction of rotation. – The direction of your extended thumb is the direction of the angular displacement vector. • A counterclockwise finger curl means the thumb is pointing in the positive direction 3/10/2021 Dr. Sasho Mac. Kenzie - HK 376 5

Link between Linear Distance and Angular Displacement • Radius is the link between linear and angular kinematics • If the angular displacement is measured in radians, then the linear distance (arc length) is equal to the angular displacement times the radius. • L = *r 3/10/2021 Dr. Sasho Mac. Kenzie - HK 376 6

Angular Velocity • The rate of change of angular displacement. • Average angular velocity equals angular displacement divided time. • The symbol is (omega). • Angular velocity is a vector found using the rt. hand rule. 3/10/2021 Dr. Sasho Mac. Kenzie - HK 376 7

Angular Distance and Angular Speed • Angular distance and angular speed define a magnitude of rotation but no direction as they are scalar quantities. 3/10/2021 Dr. Sasho Mac. Kenzie - HK 376 8

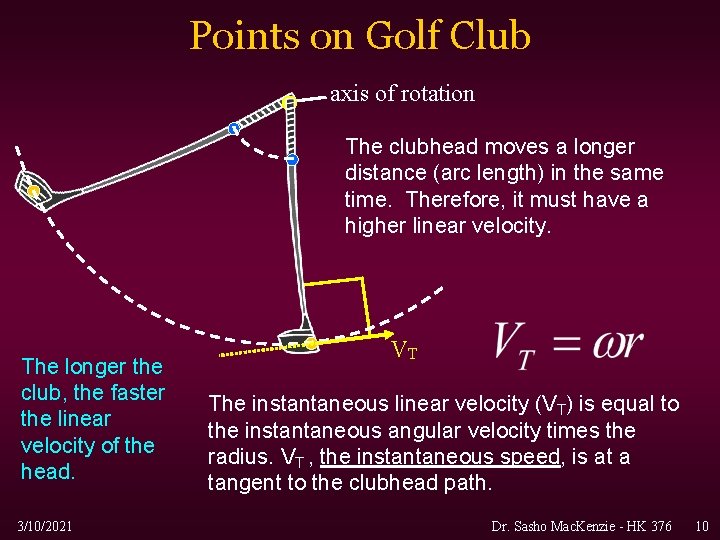
Link between Linear and Angular Velocity • The link is radius. • All points on a golf club undergo the same angular displacement and therefore the same angular velocity. • But they trace out different arc lengths based on their radius, therefore their linear velocities must be different. 3/10/2021 Dr. Sasho Mac. Kenzie - HK 376 9

Points on Golf Club axis of rotation The clubhead moves a longer distance (arc length) in the same time. Therefore, it must have a higher linear velocity. The longer the club, the faster the linear velocity of the head. 3/10/2021 VT The instantaneous linear velocity (VT) is equal to the instantaneous angular velocity times the radius. VT , the instantaneous speed, is at a tangent to the clubhead path. Dr. Sasho Mac. Kenzie - HK 376 10

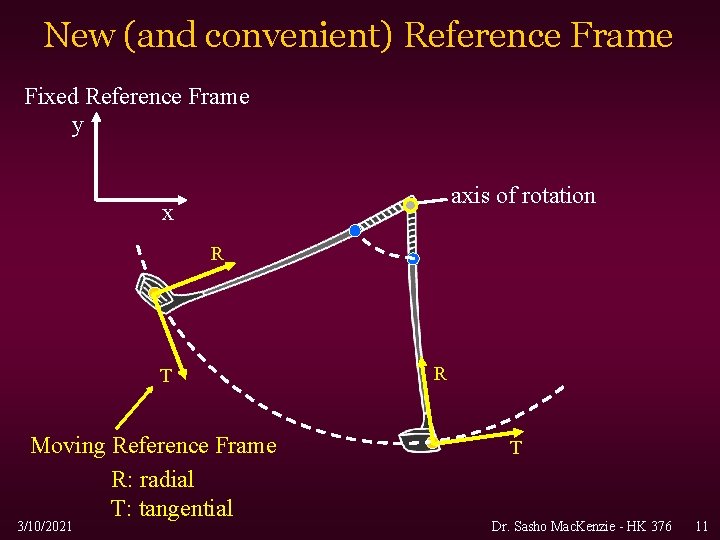
New (and convenient) Reference Frame Fixed Reference Frame y axis of rotation x R T Moving Reference Frame R: radial T: tangential 3/10/2021 R T Dr. Sasho Mac. Kenzie - HK 376 11

Angular Acceleration • The rate of change of angular velocity. • Average angular acceleration equals the change in angular velocity divided by time. • The symbol is , (alpha) • Angular acceleration is a vector found using the rt. hand rule. 3/10/2021 Dr. Sasho Mac. Kenzie - HK 376 12

Angular Acceleration • Angular acceleration occurs when something spins faster and faster or slower and slower, or when the object’s axis of spin changes direction. 3/10/2021 Dr. Sasho Mac. Kenzie - HK 376 13

Track Example Usain Bolt runs the curve of this 200 m in 11 s. Assume he ran on the inside line of lane 1, which makes a semicircle (r = 36. 5 m) for the first part of the race. His speed after the curve was 11. 5 m/s. Circle Circumference = 2 r; Circle Diameter = 2 r; r is radius 1. 2. 3. 4. Start What distance was run on the curve? What was his angular displacement ? What was his average angular velocity? What was his average angular acceleration? N 36. 5 m W E S Finish 3/10/2021 Dr. Sasho Mac. Kenzie - HK 376 14

Figure Skater Examples 1. While spinning in the air, a figure skater completes 400 degrees of rotation. What was the skater’s angular displacement covered in radians? What was the skater’s angular distance covered in radians? 2. If a figure skater has an initial angular velocity of 12 radians/second and undergoes an angular acceleration of 10 radians/second for 0. 5 seconds, what is the skater’s final angular velocity? 3/10/2021 Dr. Sasho Mac. Kenzie - HK 376 15

Linear Acceleration and Rotation When an object has angular motion, it is often easier to express linear acceleration relative to a reference frame that moves with the object. So, instead of describing acceleration in the fixed X and Y directions, we consider… • Centripetal (radial) acceleration – Calculated using angular velocity • Tangential acceleration – Calculated using angular acceleration 3/10/2021 Dr. Sasho Mac. Kenzie - HK 376 16

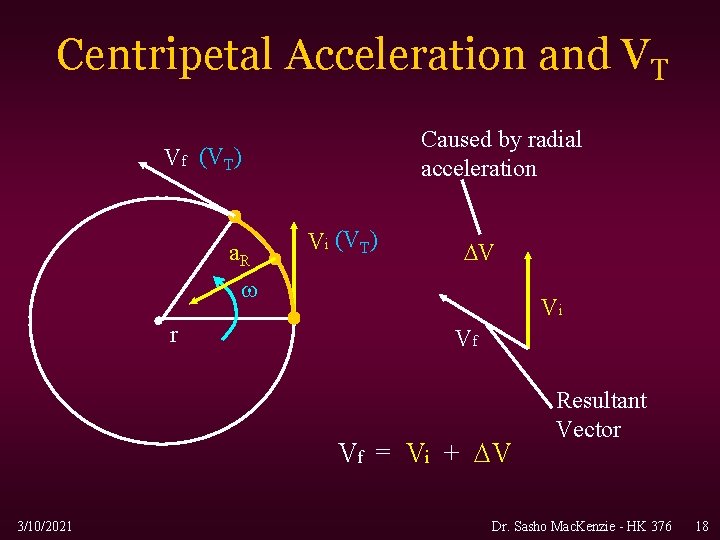
Centripetal Acceleration • The component of linear acceleration directed towards the axis of rotation (center of the circle). • Associated with the change in direction of an object moving in a circle. Changes the direction of the velocity vector (arrow). 3/10/2021 Dr. Sasho Mac. Kenzie - HK 376 17

Centripetal Acceleration and VT Caused by radial acceleration Vf (VT) a. R Vi (VT) V r Vi Vf Vf = Vi + V 3/10/2021 Resultant Vector Dr. Sasho Mac. Kenzie - HK 376 18

Tangential Acceleration • The component of linear acceleration tangent to the circular path (perpendicular to the radius). • Associated with the speeding up of an object moving in a circle. Increases the length of the tangential velocity arrow. • Equal to the angular acceleration times the radius. 3/10/2021 Dr. Sasho Mac. Kenzie - HK 376 19

Constant Angular Motion = 360 º (6. 28 rad) t = 3 s r=2 m = 0, therefore is constant at = 0, therefore Vt is constant For this example, instantaneous values are the same as average values! 3/10/2021 Dr. Sasho Mac. Kenzie - HK 376 20

Accelerated Angular Motion A = 360 º (6. 28 rad) t = 3 s B r=2 m D C Instantaneous values are different than average values! 3/10/2021 True or False 1. Between A and B, is > 0? T 2. Between D and A, is > 0? F 3. Omega ( ) is always 0? T Dr. Sasho Mac. Kenzie - HK 376 21

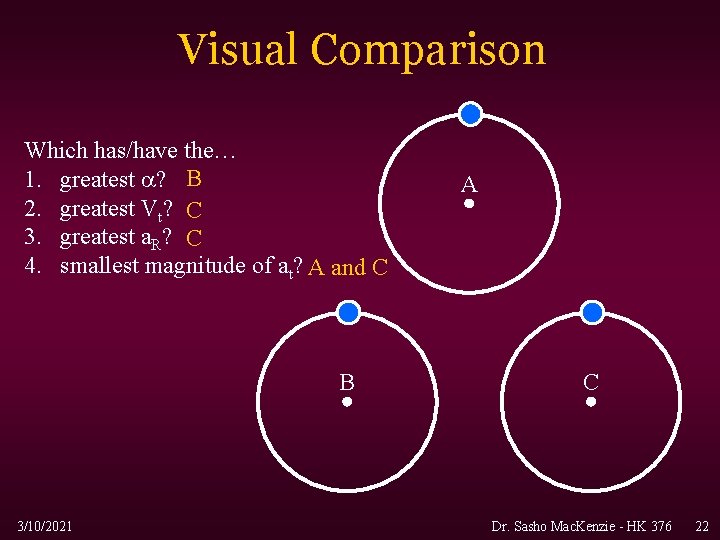
Visual Comparison Which has/have the… 1. greatest ? B 2. greatest Vt? C 3. greatest a. R? C 4. smallest magnitude of at? A and C B 3/10/2021 A C Dr. Sasho Mac. Kenzie - HK 376 22

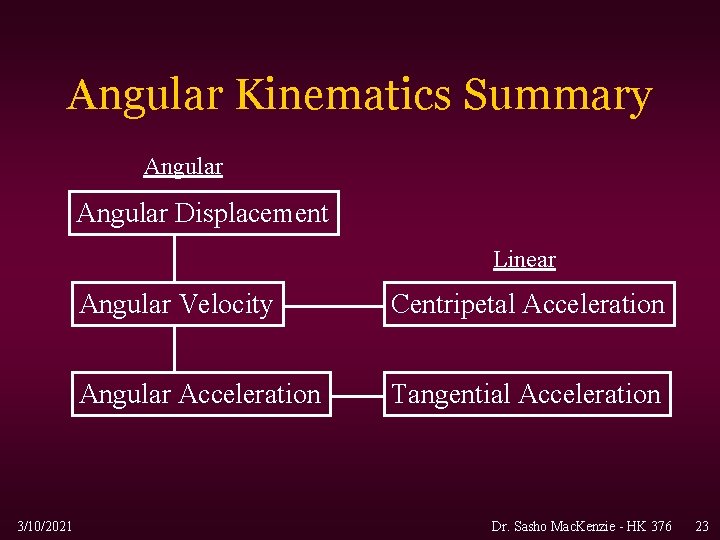
Angular Kinematics Summary Angular Displacement Linear 3/10/2021 Angular Velocity Centripetal Acceleration Angular Acceleration Tangential Acceleration Dr. Sasho Mac. Kenzie - HK 376 23

Track Example #2 At 4 s into his 200 m race, Bolt is running with a speed of 7 m/s. At 9 s, his speed is at 10 m/s. Assume he is running on the inside line of lane 1, which makes a semicircle (r = 36. 5 m). t = 4 s 1. 2. 3. 4. 5. Start N 36. 5 m t=9 s W E What’s his radial acceleration at 4 s? What’s his radial acceleration at 9 s? What’s his angular velocity at 4 s? What’s his angular velocity at 9 s? What’s his average angular acceleration between 4 s and 9 s? 6. What’s his average tangential acceleration between 4 s and 9 s? S Finish 3/10/2021 Dr. Sasho Mac. Kenzie - HK 376 24

Example Problem • The cyclists shown on the next page are rounding a turn at the bottom of a hill. The path they follow in doing this is a gentle curve that becomes progressively sharper as they near the corner. The radius of the path followed by one of these riders is 20 m at one point in the initial gentle part of the turn, and then decreases to a minimum value of 17 m, 1. 5 s later. Her tangential velocity at these two instants are 12 m/s and 11. 5 m/s respectively. What is her radial acceleration at the two points? What is her average tangential acceleration between the two points? 3/10/2021 Dr. Sasho Mac. Kenzie - HK 376 25

Biking On a Curve 3/10/2021 Dr. Sasho Mac. Kenzie - HK 376 26