Angles Triangles Demonstration This resource provides animated demonstrations

Angles – Triangles – Demonstration This resource provides animated demonstrations of the mathematical method. Check animations and delete slides not needed for your class.

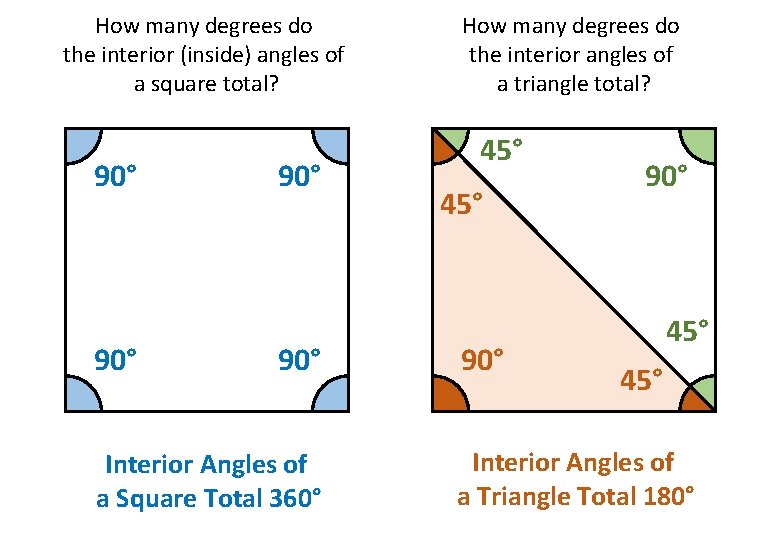
How many degrees do the interior (inside) angles of a square total? 90° 90° Interior Angles of a Square Total 360° How many degrees do the interior angles of a triangle total? 45° 90° 45° Interior Angles of a Triangle Total 180°

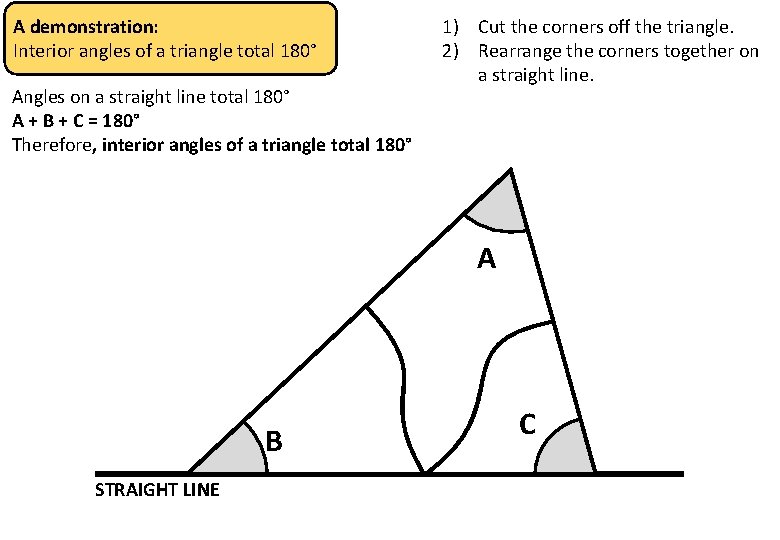
A demonstration: Interior angles of a triangle total 180° Angles on a straight line total 180° A + B + C = 180° Therefore, interior angles of a triangle total 180° 1) Cut the corners off the triangle. 2) Rearrange the corners together on a straight line. A B STRAIGHT LINE C

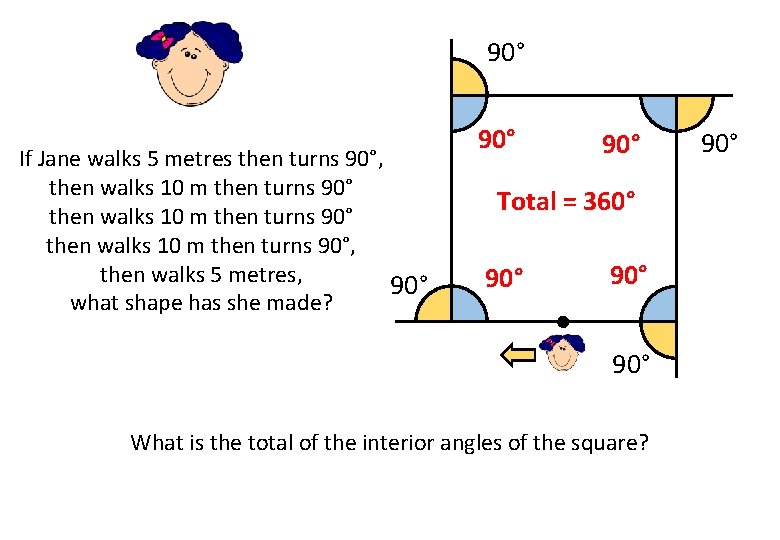
90° If Jane walks 5 metres then turns 90°, then walks 10 m then turns 90°, then walks 5 metres, 90° what shape has she made? 90° Total = 360° 90° 90° What is the total of the interior angles of the square? 90°

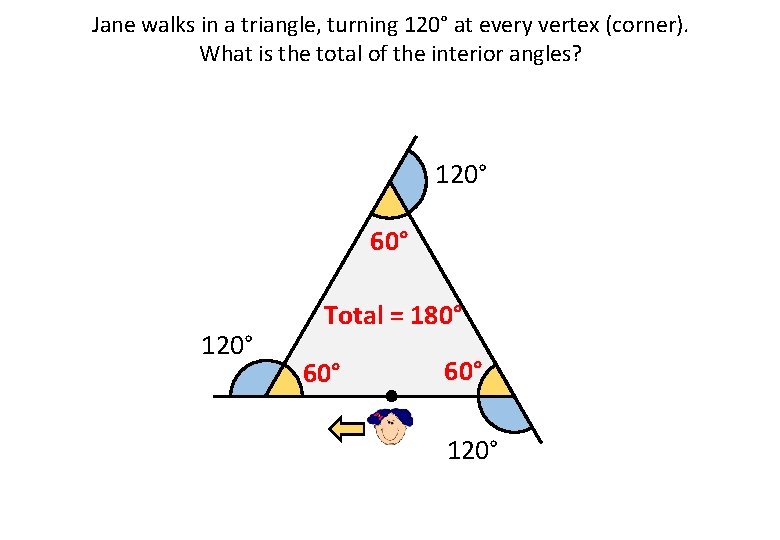
Jane walks in a triangle, turning 120° at every vertex (corner). What is the total of the interior angles? 120° 60° 120° Total = 180° 60° 120°

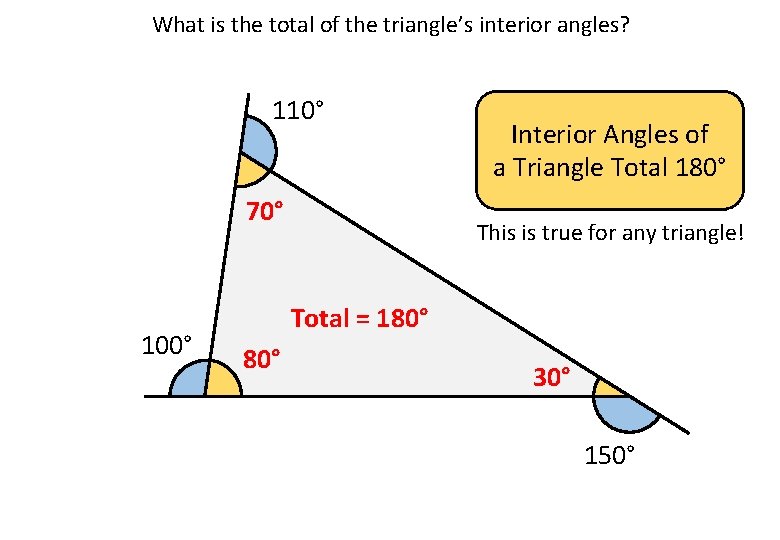
What is the total of the triangle’s interior angles? 110° 70° 100° Interior Angles of a Triangle Total 180° This is true for any triangle! Total = 180° 30° 150°

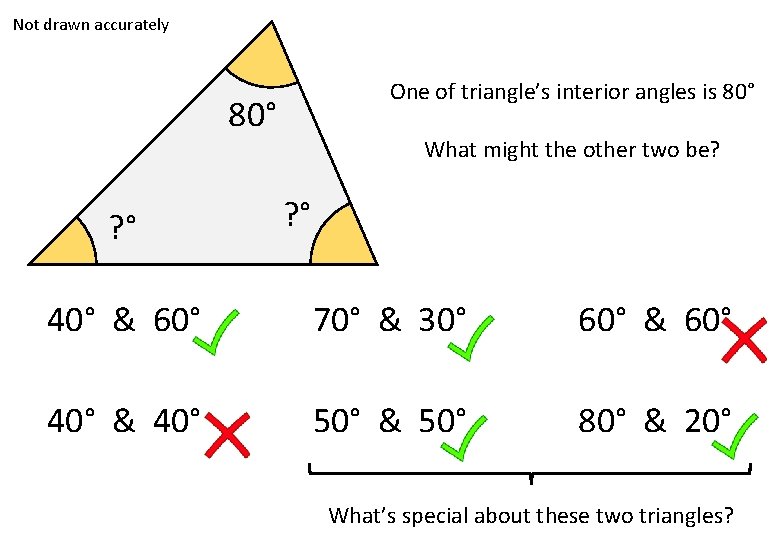
Not drawn accurately One of triangle’s interior angles is 80° ? ° What might the other two be? ? ° 40° & 60° 70° & 30° 60° & 60° 40° & 40° 50° & 50° 80° & 20° What’s special about these two triangles?

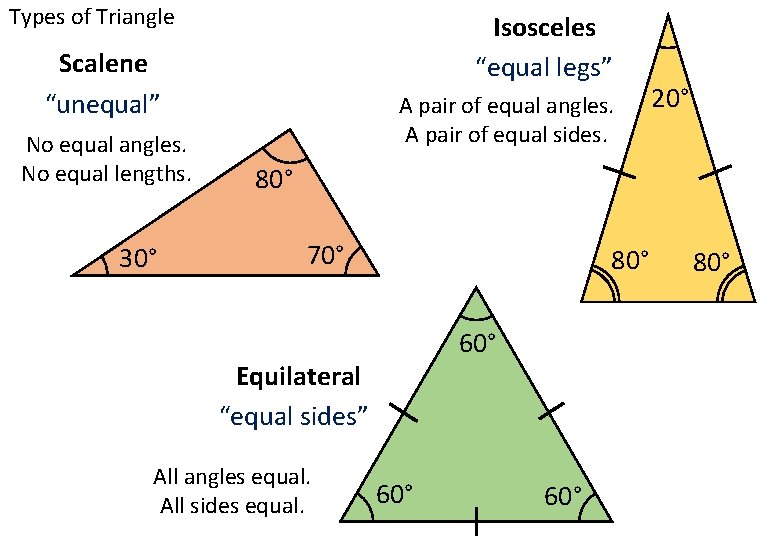
Types of Triangle Isosceles “equal legs” Scalene “unequal” No equal angles. No equal lengths. 30° A pair of equal angles. A pair of equal sides. 20° 80° 70° 80° 60° Equilateral “equal sides” All angles equal. All sides equal. 60° 80°

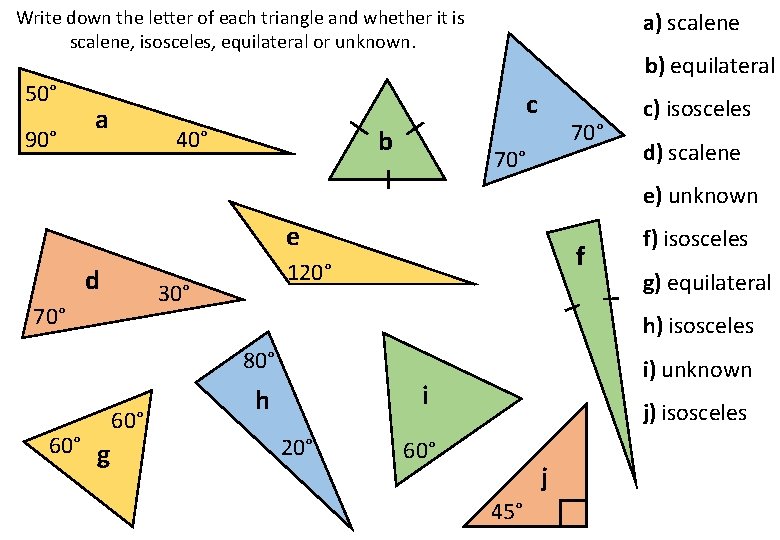
Write down the letter of each triangle and whether it is scalene, isosceles, equilateral or unknown. 50° 90° a) scalene b) equilateral c a b 40° 70° c) isosceles d) scalene e) unknown e d 30° 70° f 120° g) equilateral h) isosceles 80° 60° g f) isosceles 60° i) unknown i h 20° j) isosceles 60° j 45°

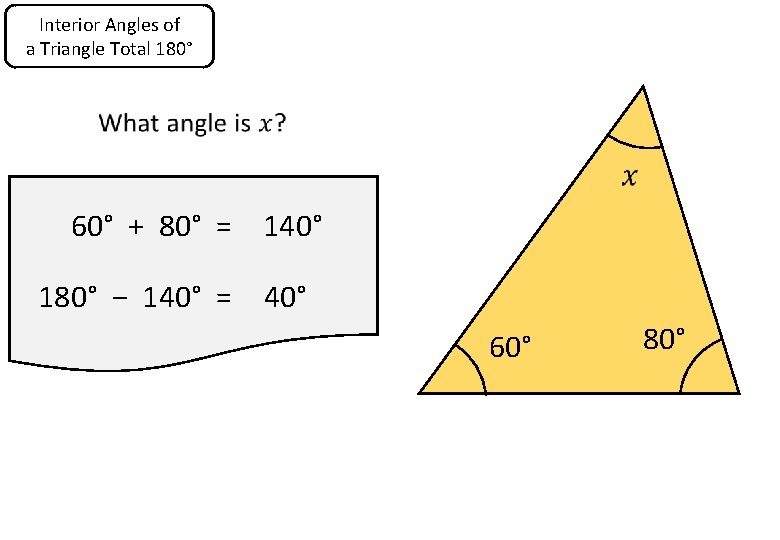
Interior Angles of a Triangle Total 180° 60° + 80° = 140° 180° − 140° = 40° 60° 80°

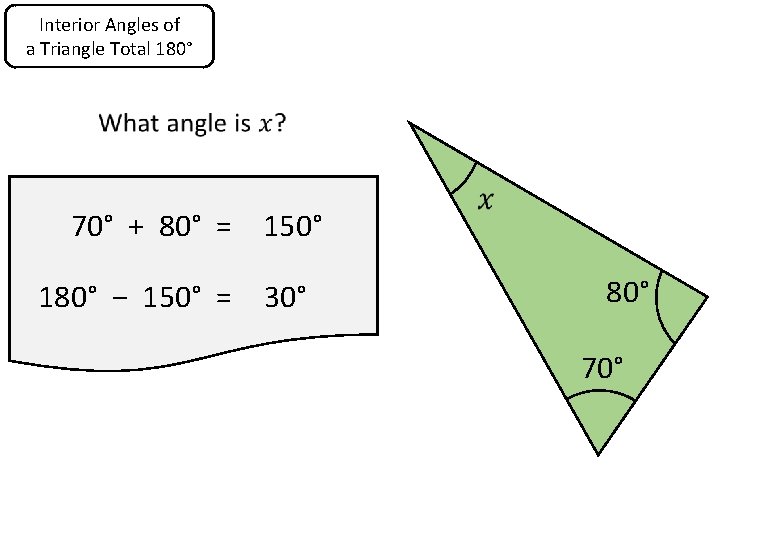
Interior Angles of a Triangle Total 180° 70° + 80° = 150° 180° − 150° = 30° 80° 70°

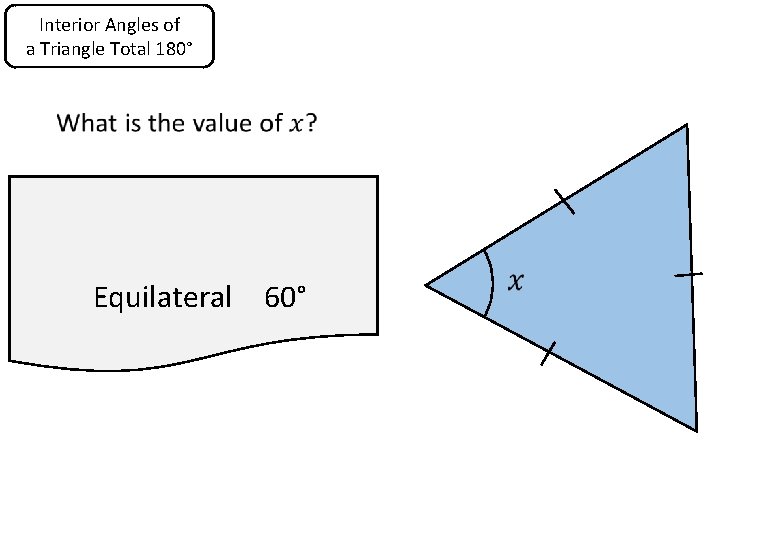
Interior Angles of a Triangle Total 180° Equilateral 60°

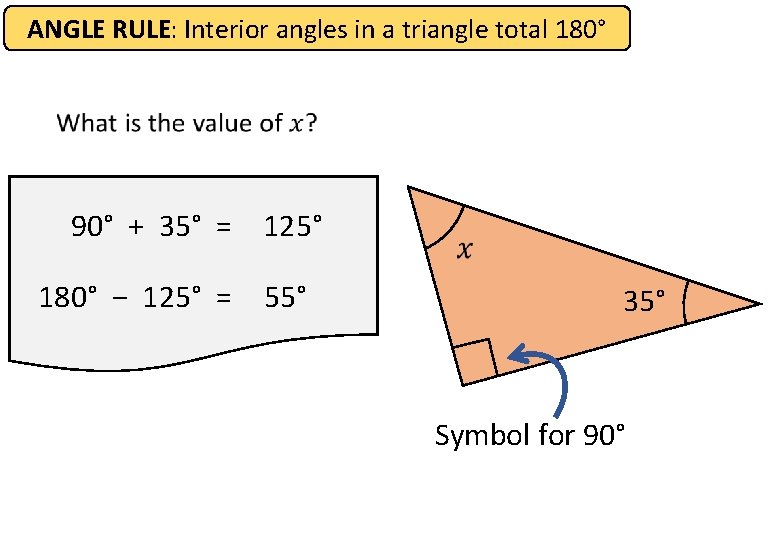
ANGLE RULE: Interior angles in a triangle total 180° 90° + 35° = 125° 180° − 125° = 55° 35° Symbol for 90°

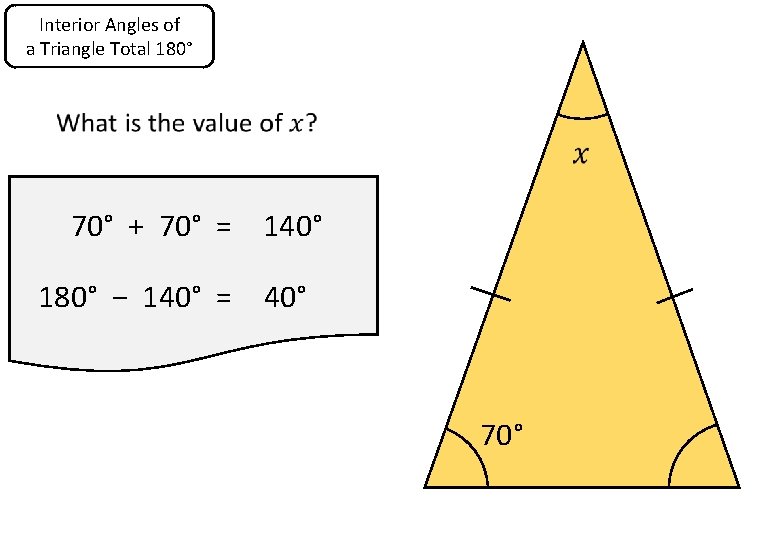
Interior Angles of a Triangle Total 180° 70° + 70° = 140° 180° − 140° = 40° 70°

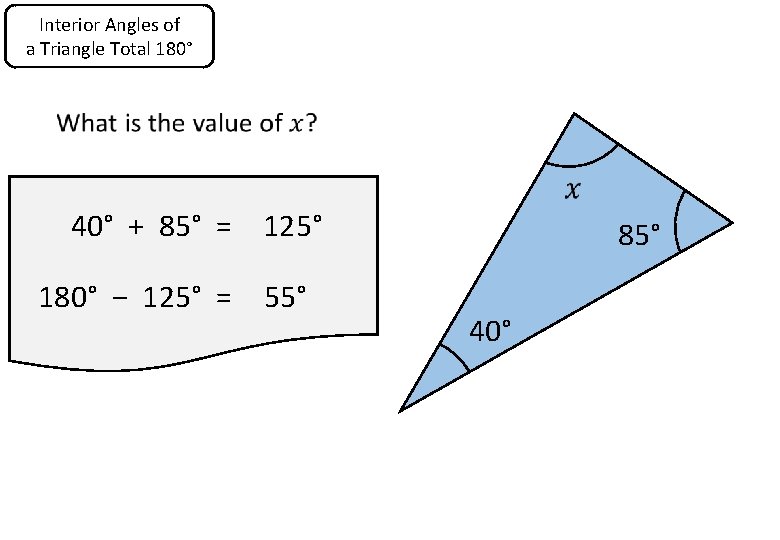
Interior Angles of a Triangle Total 180° 40° + 85° = 125° 180° − 125° = 55° 85° 40°

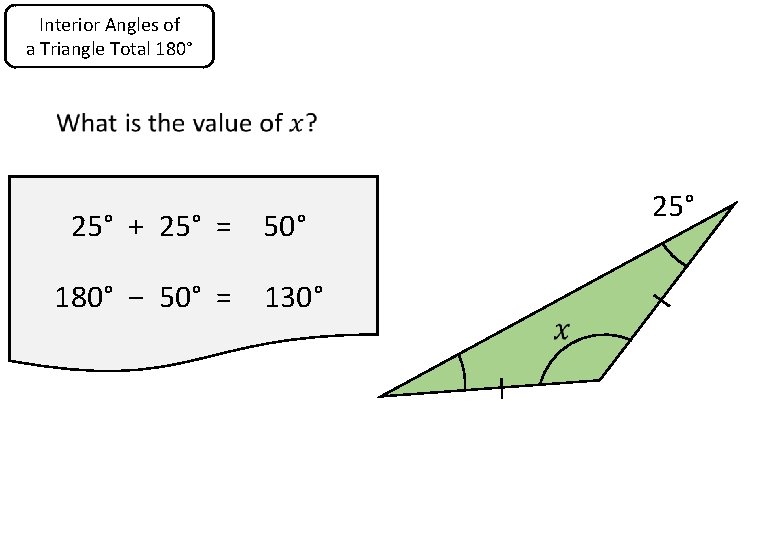
Interior Angles of a Triangle Total 180° 25° + 25° = 50° 180° − 50° = 130° 25°

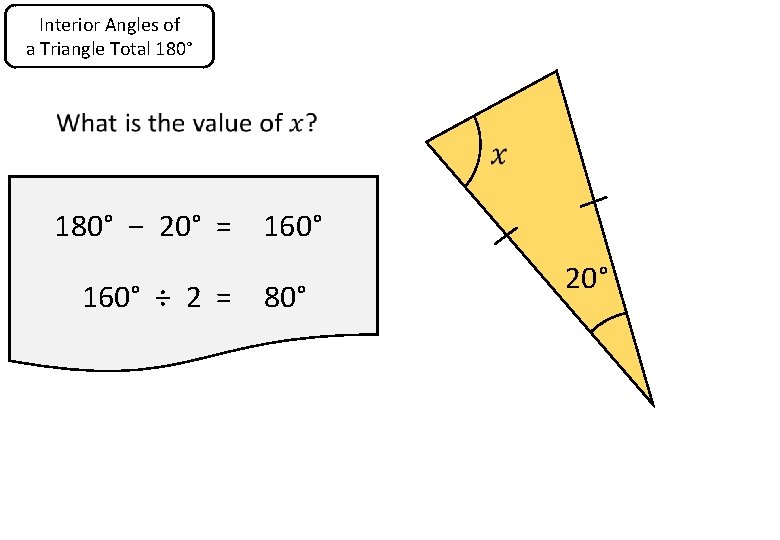
Interior Angles of a Triangle Total 180° − 20° = 160° ÷ 2 = 80° 20°

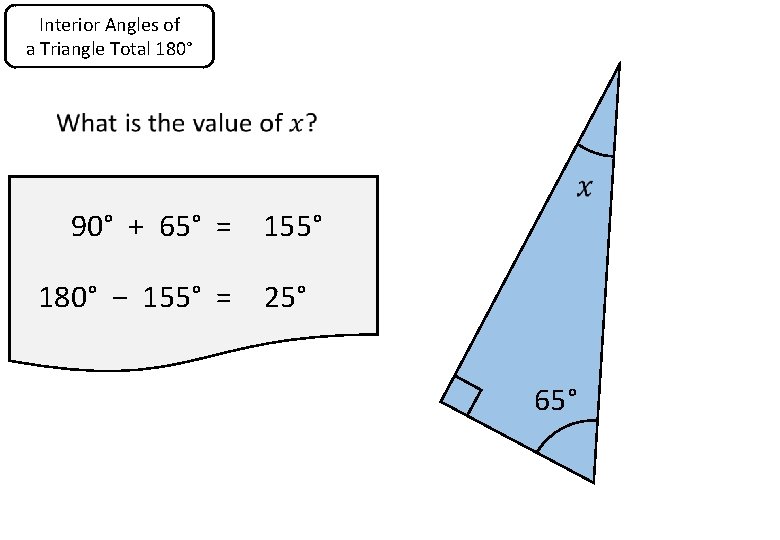
Interior Angles of a Triangle Total 180° 90° + 65° = 155° 180° − 155° = 25° 65°

Questions? Comments? Suggestions? …or have you found a mistake!? Any feedback would be appreciated . Please feel free to email: tom@goteachmaths. co. uk