Angles Triangles Activity A Printing To print handouts

Angles – Triangles – Activity A

Printing To print handouts from slides Select the slide from the left. Then click: File > Print > ‘Print Current Slide’ To print multiple slides Click on a section title to highlight all those slides, or press ‘Ctrl’ at the same time as selecting slides to highlight more than one. Then click: File > Print > ‘Print Selection’ To print double-sided handouts Highlight both slides before using ‘Print Selection’. Choose ‘Print on Both Sides’ and ‘Flip on Short Edge’.

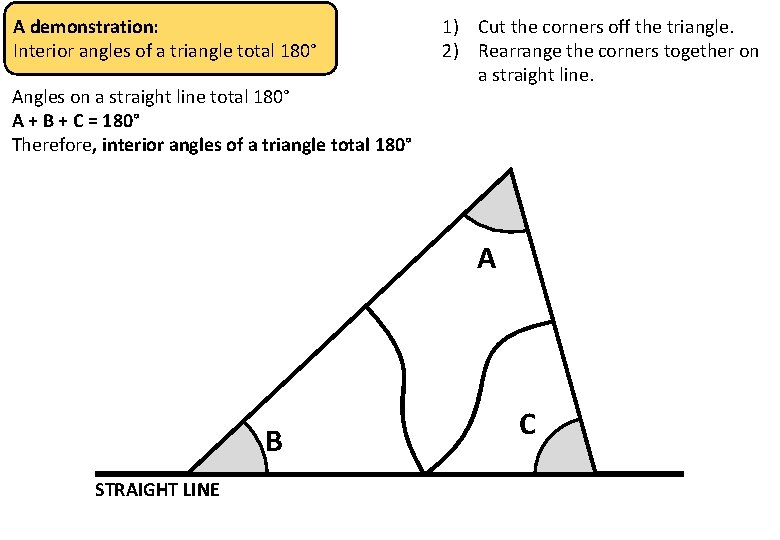
A demonstration: Interior angles of a triangle total 180° Angles on a straight line total 180° A + B + C = 180° Therefore, interior angles of a triangle total 180° 1) Cut the corners off the triangle. 2) Rearrange the corners together on a straight line. A B STRAIGHT LINE C

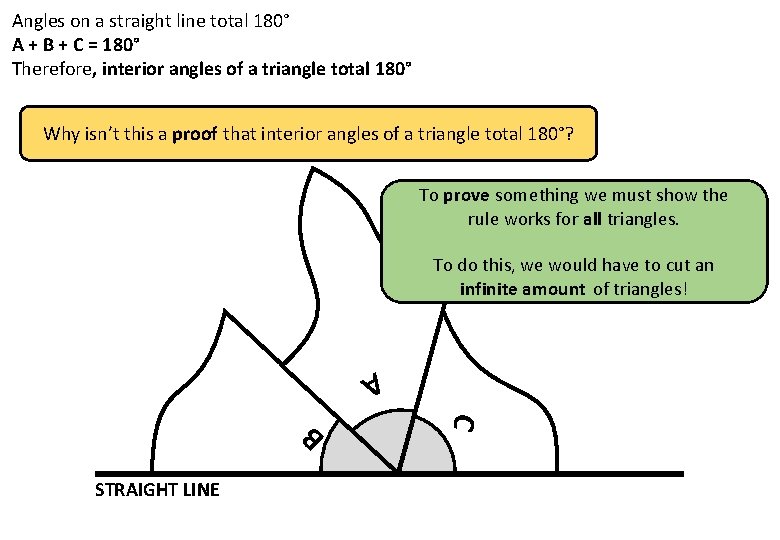
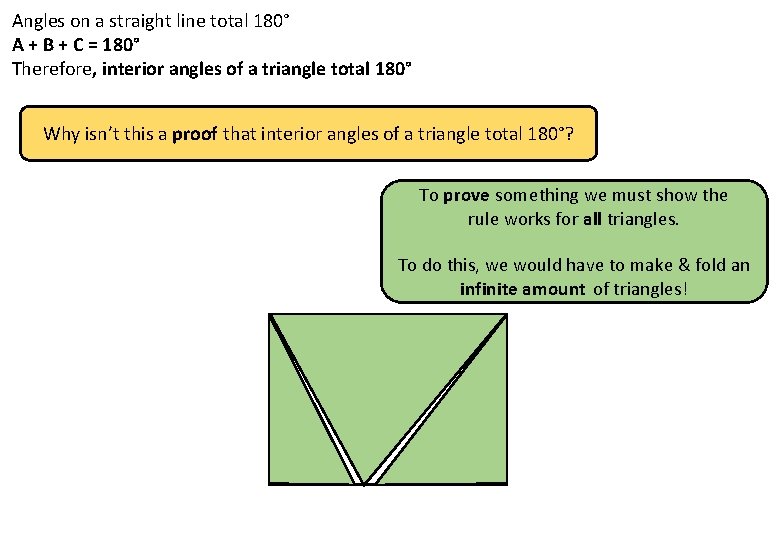
Angles on a straight line total 180° A + B + C = 180° Therefore, interior angles of a triangle total 180° Why isn’t this a proof that interior angles of a triangle total 180°? To prove something we must show the rule works for all triangles. To do this, we would have to cut an infinite amount of triangles! A C B STRAIGHT LINE

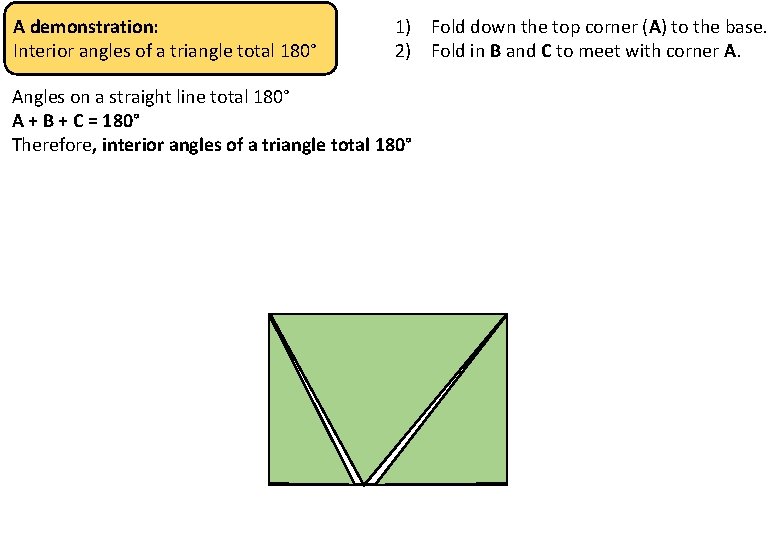
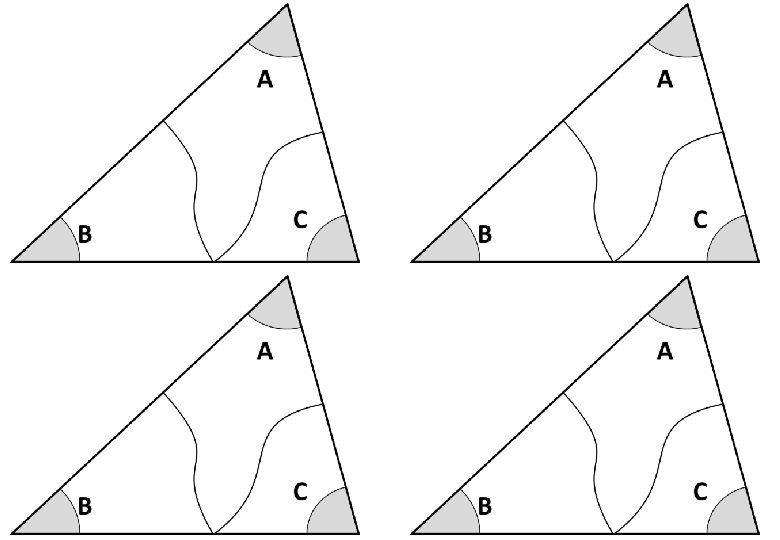
1) Fold down the top corner (A) to the base. 2) Fold in B and C to meet with corner A. A demonstration: Interior angles of a triangle total 180° Angles on a straight line total 180° A + B + C = 180° Therefore, interior angles of a triangle total 180° A B C

Angles on a straight line total 180° A + B + C = 180° Therefore, interior angles of a triangle total 180° Why isn’t this a proof that interior angles of a triangle total 180°? A To prove something we must show the rule works for all triangles. To do this, we would have to make & fold an infinite amount of triangles! B C

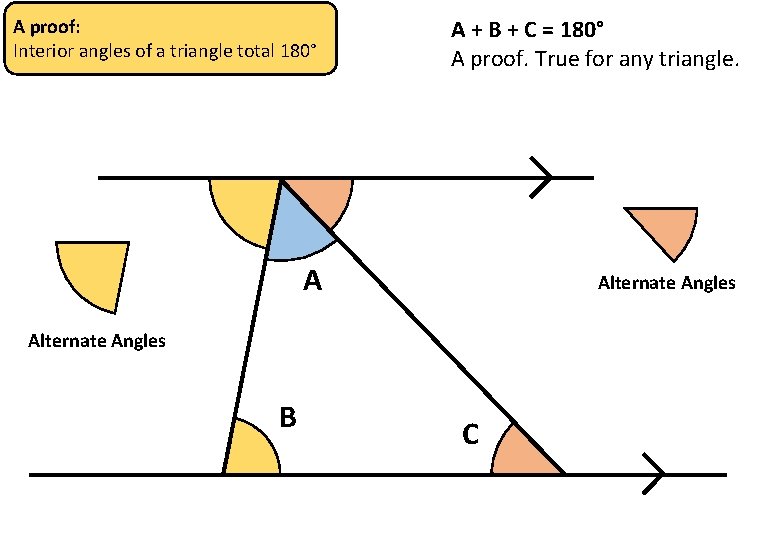
A proof: Interior angles of a triangle total 180° A + B + C = 180° A proof. True for any triangle. A Alternate Angles B C

Questions? Comments? Suggestions? …or have you found a mistake!? Any feedback would be appreciated . Please feel free to email: tom@goteachmaths. co. uk