Angles Regular Polygons Complete Lesson Preview the presentation

Angles – Regular Polygons – Complete Lesson Preview the presentation to check ability-level, AFL questions, and the animations during demonstrations. It is recommended to delete slides/sections not needed for your class.

Starter A task at the beginning of the lesson that reviews a skill required for the learning. Knowledge Check Questions to assess students’ current understanding and to consequently show progress. Real-Life Example A ‘hook’ to raise interest and provide a concrete example. Demonstration Slides for a teacher to lead students – didactically or via questioning – through a mathematical method. AFL Questions Assessment For Learning Questions, used to assess students’ competency for independent tasks/activities. Plenary An opportunity for students to prove/evaluate their learning.

Printing To print handouts from slides Select the slide from the left. Then click: File > Print > ‘Print Current Slide’ To print multiple slides Click on a section title to highlight all those slides, or press ‘Ctrl’ at the same time as selecting slides to highlight more than one. Then click: File > Print > ‘Print Selection’ To print double-sided handouts Highlight both slides before using ‘Print Selection’. Choose ‘Print on Both Sides’ and ‘Flip on Short Edge’.

Use the numbers below to make… Count 226 8 6 9 3 UP 4 5 2 1

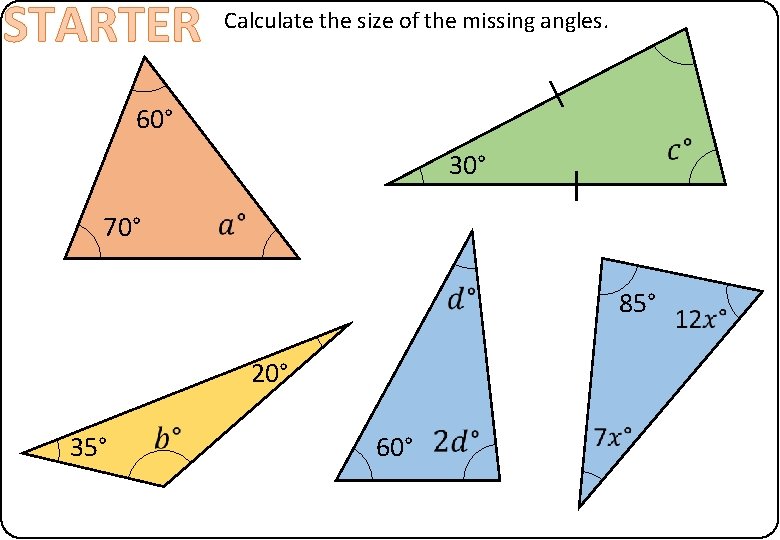
STARTER Calculate the size of the missing angles. 60° 30° 70° 85° 20° 35° 60°

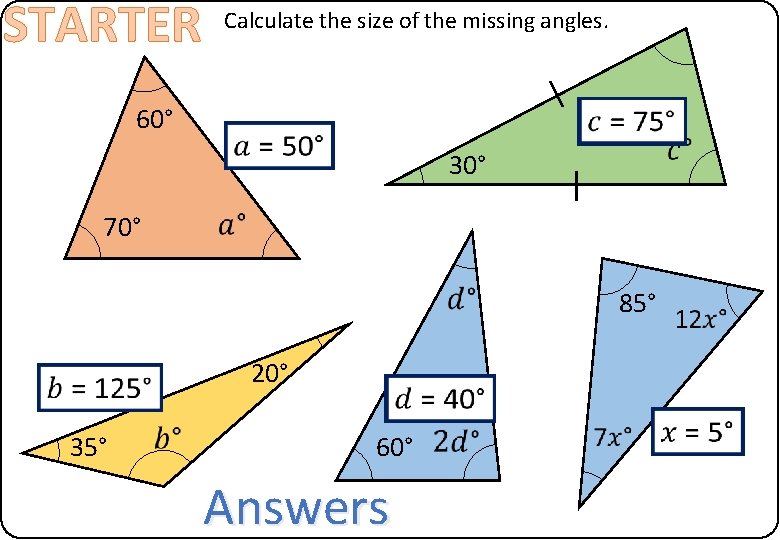
STARTER Calculate the size of the missing angles. 60° 30° 70° 85° 20° 35° 60° Answers

June 2021 Interior & Exterior Angles of Regular Polygons

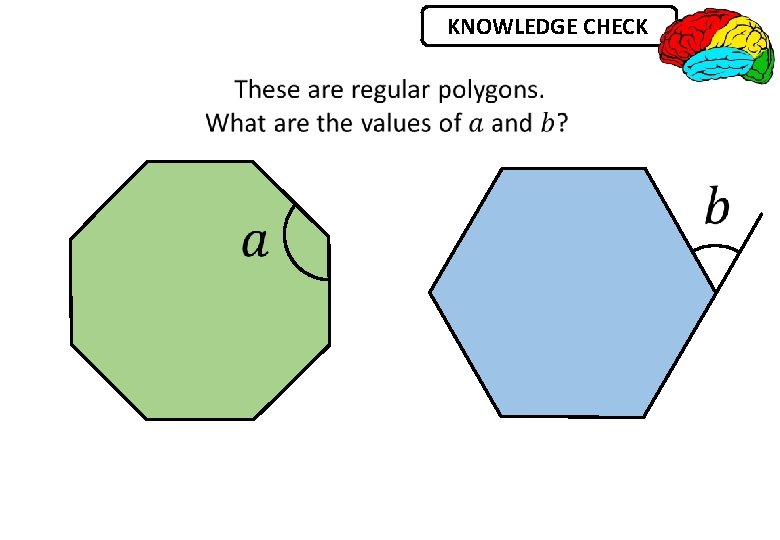
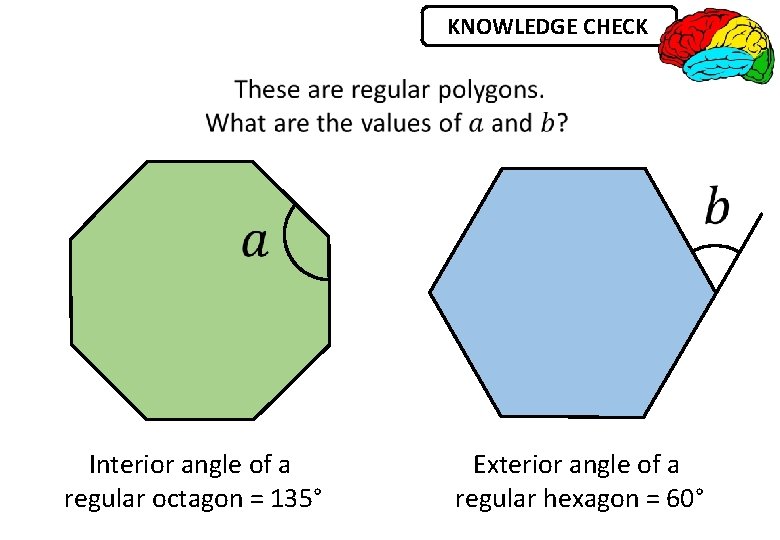
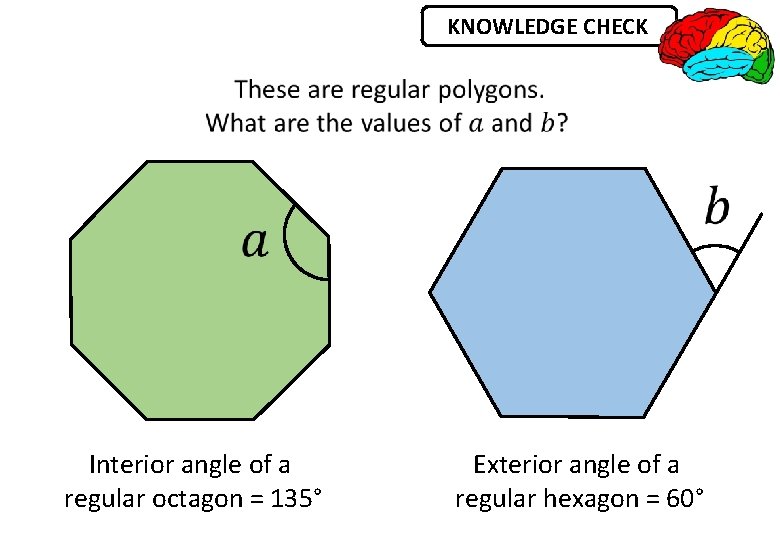
KNOWLEDGE CHECK

KNOWLEDGE CHECK Interior angle of a regular octagon = 135° Exterior angle of a regular hexagon = 60°

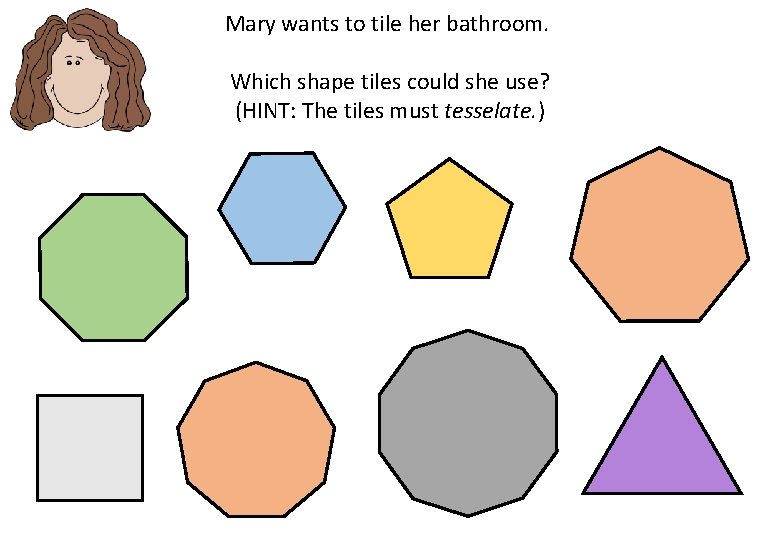
Mary wants to tile her bathroom. Which shape tiles could she use? (HINT: The tiles must tesselate. )

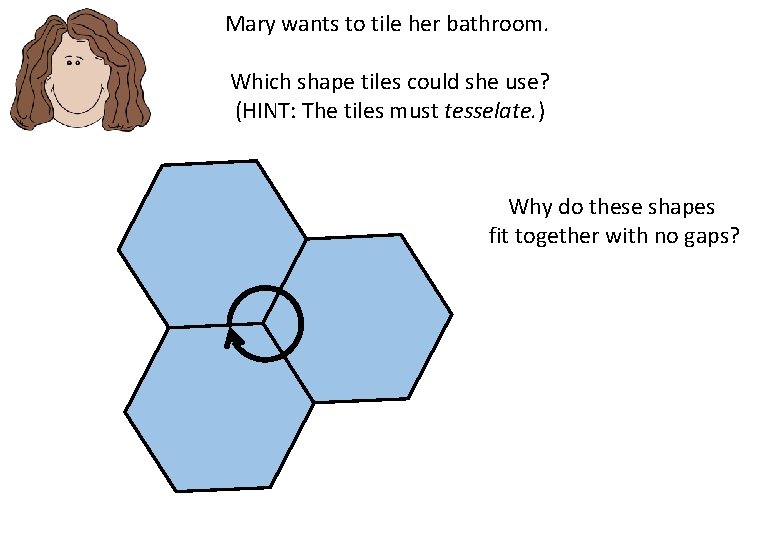
Mary wants to tile her bathroom. Which shape tiles could she use? (HINT: The tiles must tesselate. ) Why do these shapes fit together with no gaps?

Mary wants to tile her bathroom. Which shape tiles could she use? (HINT: The tiles must tesselate. ) Why do these shapes fit together with no gaps?

Mary wants to tile her bathroom. Which shape tiles could she use? (HINT: The tiles must tesselate. ) Why do these shapes fit together with no gaps?

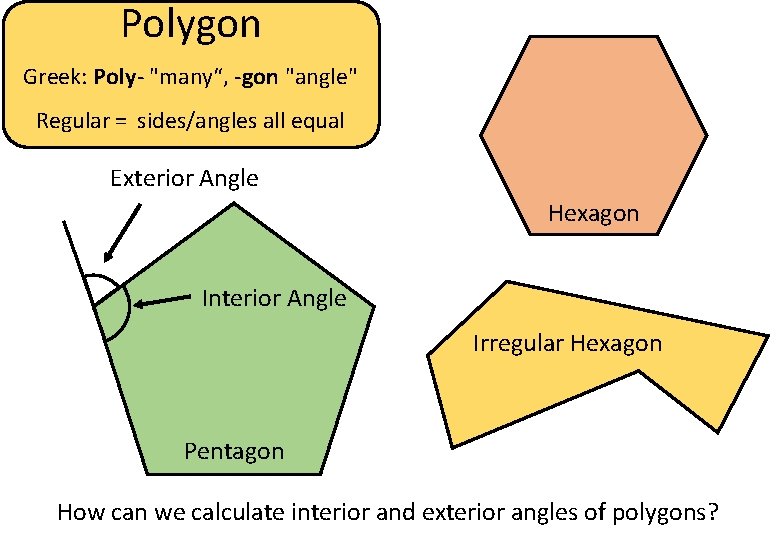
Polygon Greek: Poly- "many“, -gon "angle" Regular = sides/angles all equal 3. 2. 1. 5. Which of these shapes are polygons? Which are regular? Which are irregular? Can you name them? 6. 4. 7. 8. 10. 9. 11. 12.

Polygon Greek: Poly- "many“, -gon "angle" Regular = sides/angles all equal Regular Hexagon 2. 1. 5. 6. Which of these shapes are polygons? Which are regular? Which are irregular? Can you name them? Irregular Hexagon 3. Regular Decagon 4. Irregular Octagon 7. Irregular Hexagon 8. 11. 10. Regular Octagon 12. 9. Regular Pentagon Regular Triangle

Polygon Greek: Poly- "many“, -gon "angle" Regular = sides/angles all equal Exterior Angle Hexagon Interior Angle Irregular Hexagon Pentagon How can we calculate interior and exterior angles of polygons?

We know the interior angles of a triangle total 180°. 60° 50° How can we work out the interior angles of a quadrilateral? 70° If we divide it into 2 triangles, we can see the interior angles must total 360°.

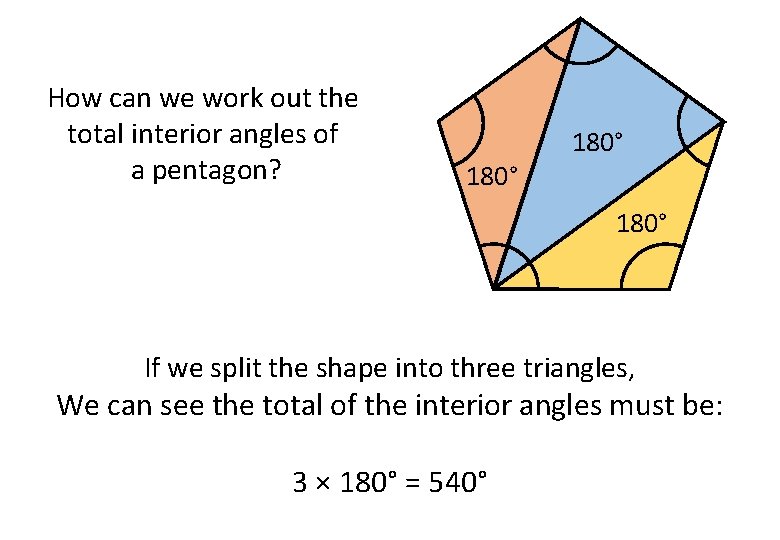
How can we work out the total interior angles of a pentagon? 180° If we split the shape into three triangles, We can see the total of the interior angles must be: 3 × 180° = 540°

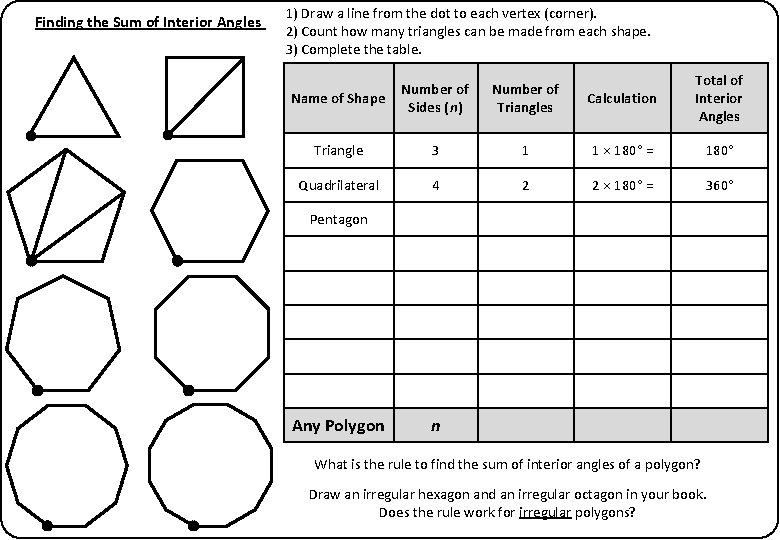
Finding the Sum of Interior Angles 1) Draw a line from the dot to each vertex (corner). 2) Count how many triangles can be made from each shape. 3) Complete the table. Name of Shape Number of Sides (n) Number of Triangles Calculation Total of Interior Angles Triangle 3 1 1 × 180° = 180° Quadrilateral 4 2 2 × 180° = 360° Pentagon Any Polygon n What is the rule to find the sum of interior angles of a polygon? Draw an irregular hexagon and an irregular octagon in your book. Does the rule work for irregular polygons?

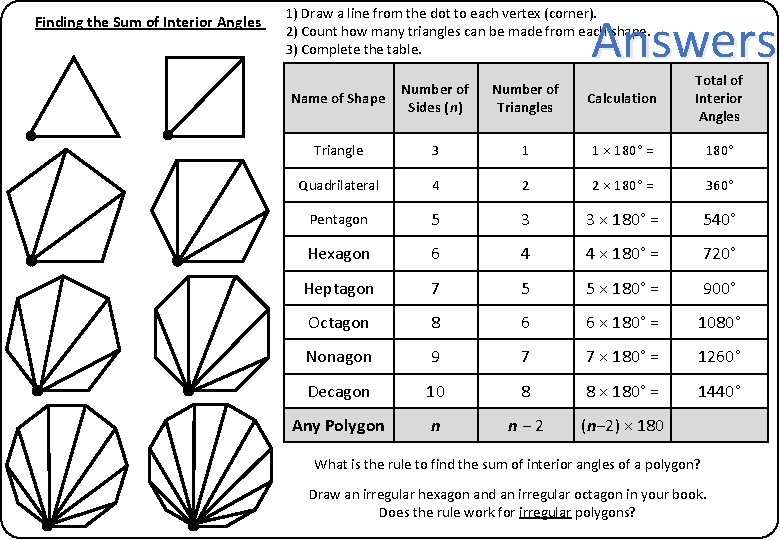
Finding the Sum of Interior Angles 1) Draw a line from the dot to each vertex (corner). 2) Count how many triangles can be made from each shape. 3) Complete the table. Answers Name of Shape Number of Sides (n) Number of Triangles Calculation Total of Interior Angles Triangle 3 1 1 × 180° = 180° Quadrilateral 4 2 2 × 180° = 360° Pentagon 5 3 3 × 180° = 540° Hexagon 6 4 4 × 180° = 720° Heptagon 7 5 5 × 180° = 900° Octagon 8 6 6 × 180° = 1080° Nonagon 9 7 7 × 180° = 1260° Decagon 10 8 8 × 180° = 1440° Any Polygon n n− 2 (n− 2) × 180 What is the rule to find the sum of interior angles of a polygon? Draw an irregular hexagon and an irregular octagon in your book. Does the rule work for irregular polygons?

We can see that any polygon can be divided into triangles. The amount of triangles is two less than the number of sides (n). Regular Pentagon Irregular Octagon Total Interior Angles = 3 × 180° = 540° Total Interior Angles = 6 × 180° = 1080° The formula for any regular or irregular polygon is: Sum of Interior Angles = (n− 2) × 180

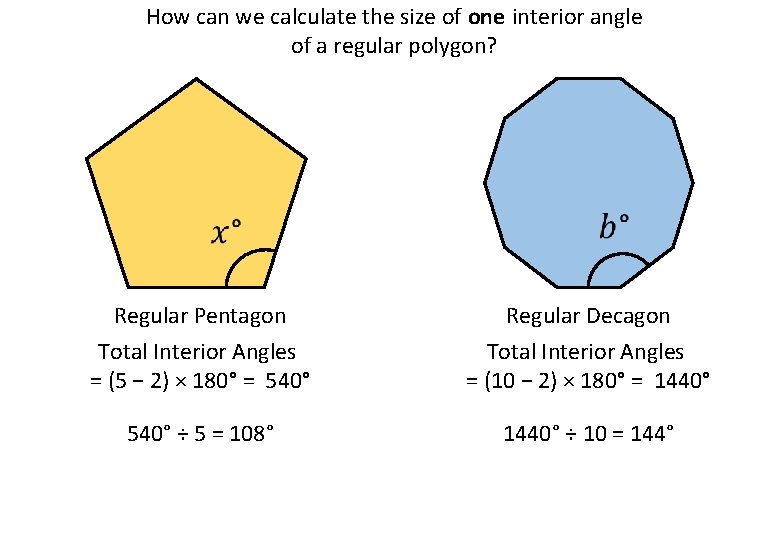
How can we calculate the size of one interior angle of a regular polygon? Regular Pentagon Regular Decagon Total Interior Angles = (5 − 2) × 180° = 540° Total Interior Angles = (10 − 2) × 180° = 1440° 540° ÷ 5 = 108° 1440° ÷ 10 = 144°

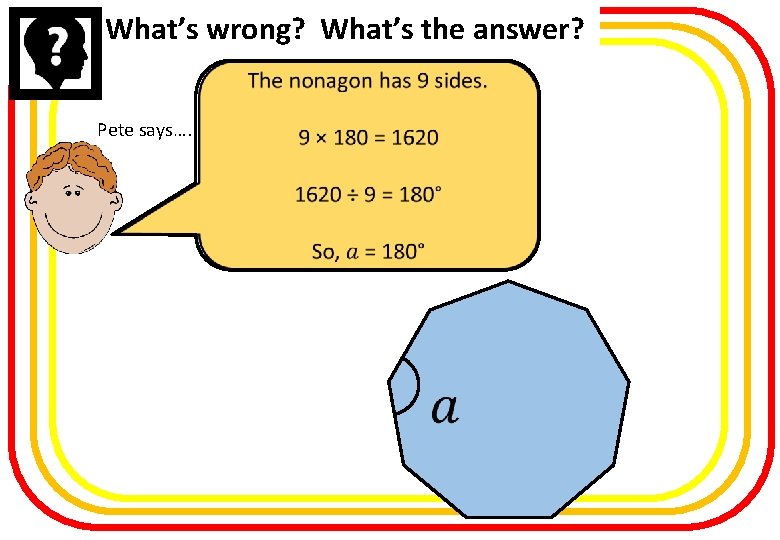
What’s wrong? What’s the answer? Pete says….

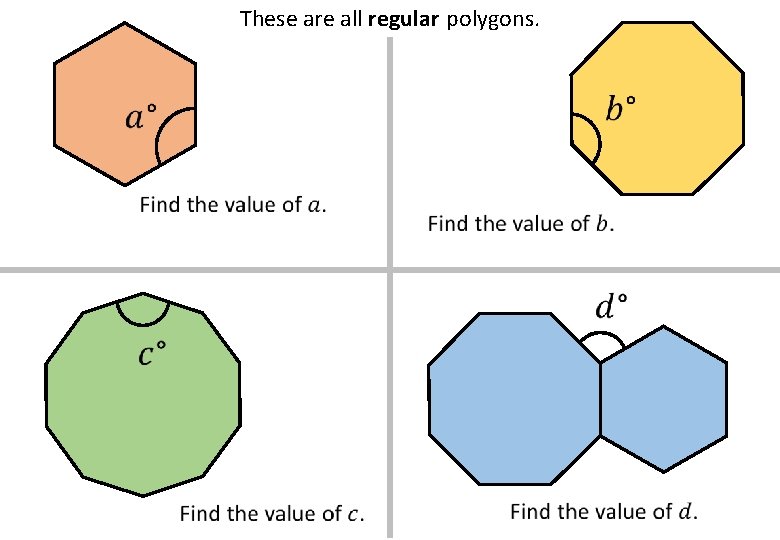
These are all regular polygons.

These are all regular polygons. Answers

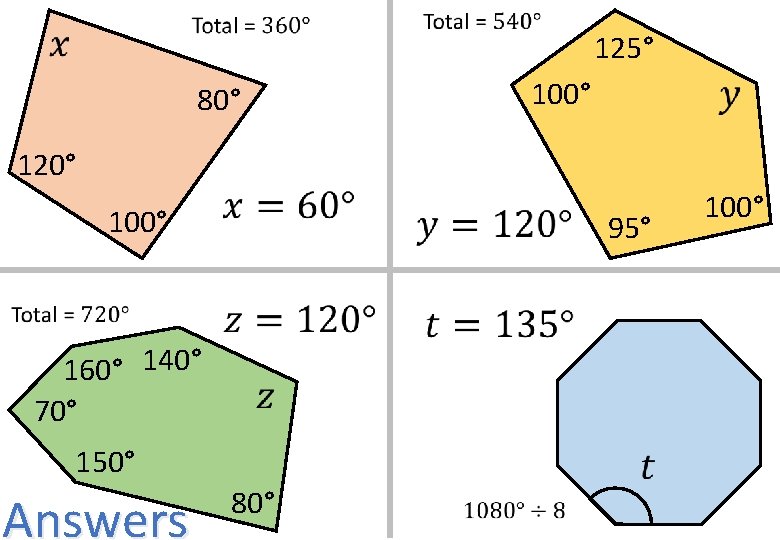
125° 80° 100° 120° 100° 95° 160° 140° 70° 150° 80° 100°

125° 80° 100° 120° 100° 95° 160° 140° 70° 150° Answers 80° 100°

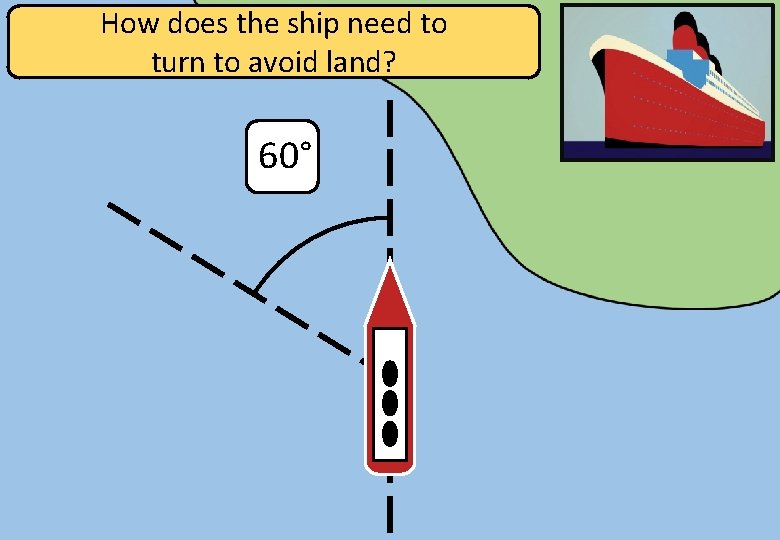
How does the ship need to turn to avoid land? 60°

The ship wants to sail in a rectangle around the island. What is the total of the four turns? 90° 4 × 90° = 360° 90°

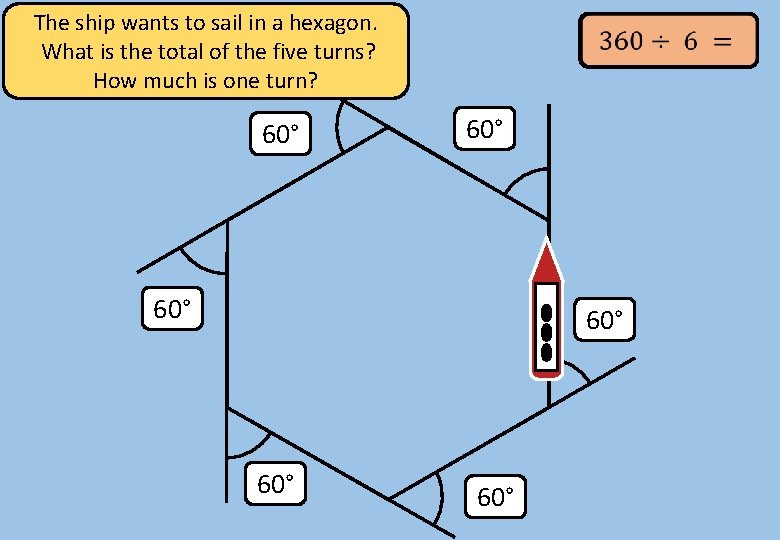
The ship wants to sail in a hexagon. What is the total of the five turns? How much is one turn? 60° 60° 60°

The ship wants to sail in a pentagon. What is the total of the five turns? How much is one turn? 72° 72° 72°

The ship is going to describe an irregular octagon. What is the total of the eight turns? 20° 50° 100 + 20 + 50 + 80 + 40 +70 = 360° 80° 40° 70°

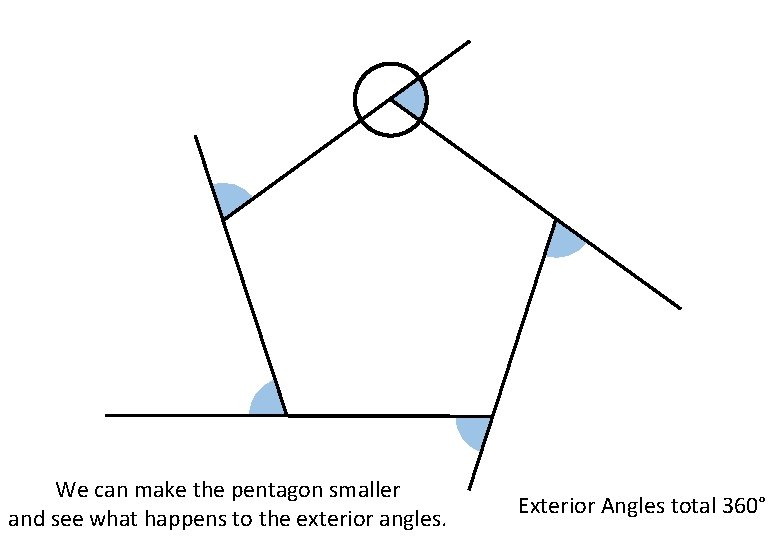
We can make the pentagon smaller and see what happens to the exterior angles. Exterior Angles total 360°

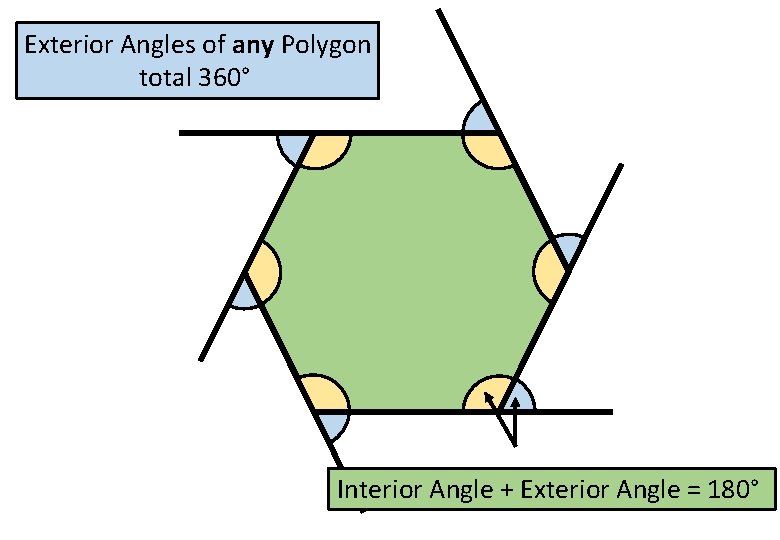
Exterior Angles of any Polygon total 360° Interior Angle + Exterior Angle = 180°

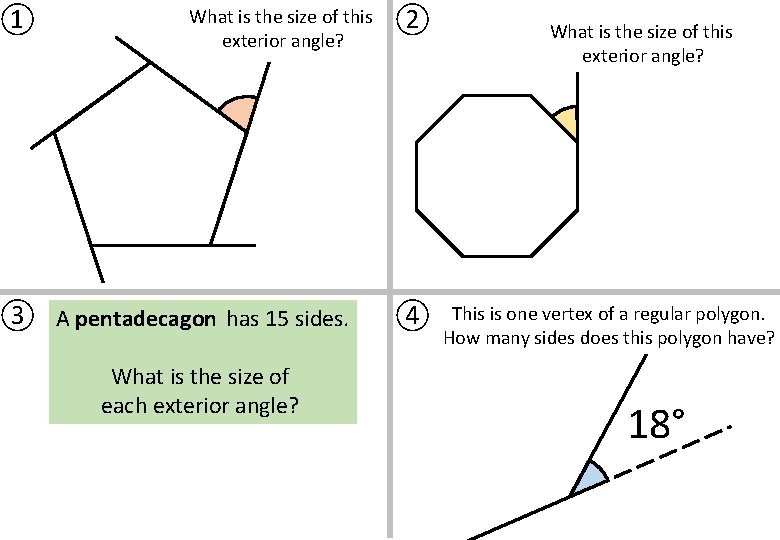
① What is the size of this exterior angle? ③ A pentadecagon has 15 sides. What is the size of each exterior angle? ② ④ What is the size of this exterior angle? This is one vertex of a regular polygon. How many sides does this polygon have? 18°

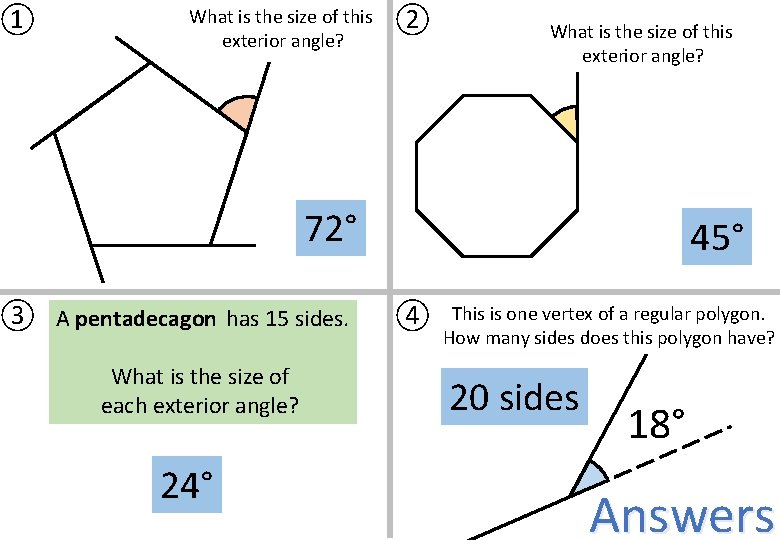
① What is the size of this exterior angle? ② What is the size of this exterior angle? 72° ③ A pentadecagon has 15 sides. What is the size of each exterior angle? 24° 45° ④ This is one vertex of a regular polygon. How many sides does this polygon have? 20 sides 18° Answers

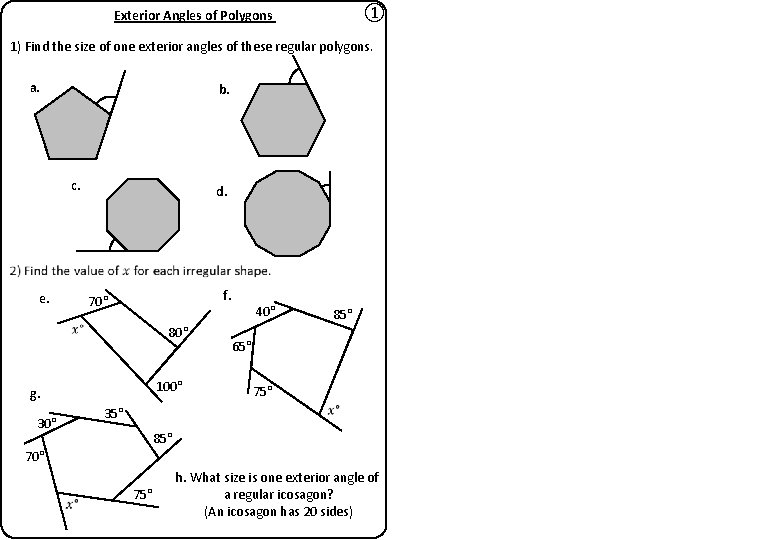
① Exterior Angles of Polygons 1) Find the size of one exterior angles of these regular polygons. a. b. c. e. d. f. 70° 80° 100° g. 30° 40° 85° 65° 75° 35° 85° 70° 75° h. What size is one exterior angle of a regular icosagon? (An icosagon has 20 sides)

① Exterior Angles of Polygons 1) Find the size of one exterior angles of these regular polygons. a. b. c. e. d. f. 70° 80° 100° g. 30° 40° 85° 65° 75° 35° 85° 70° 75° h. What size is one exterior angle of a regular icosagon? (An icosagon has 20 sides) Answers a) 72° b) 60° c) 45° d) 30° e) 110° f) 95° g) 65° h) 18°

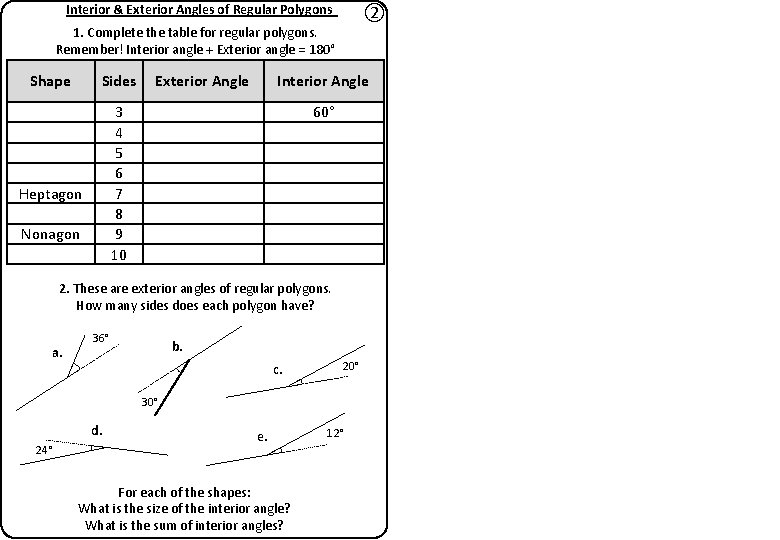
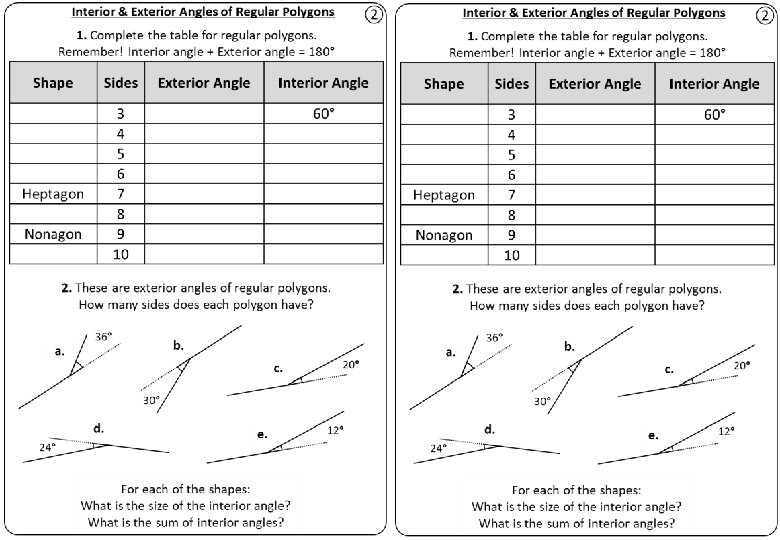
Interior & Exterior Angles of Regular Polygons ② 1. Complete the table for regular polygons. Remember! Interior angle + Exterior angle = 180° Shape Sides Exterior Angle Interior Angle 3 4 5 6 7 8 9 10 Heptagon Nonagon 60° 2. These are exterior angles of regular polygons. How many sides does each polygon have? a. 36° b. c. 20° 30° d. 24° e. For each of the shapes: What is the size of the interior angle? What is the sum of interior angles? 12°

Interior & Exterior Angles of Regular Polygons ② 1. Complete the table for regular polygons. Remember! Interior angle + Exterior angle = 180° Shape Sides Exterior Angle Interior Angle Triangle Quadrilateral Pentagon Hexagon Heptagon Octagon Nonagon Decagon 3 4 5 6 7 8 9 10 120° 90° 72° 60° 51. 4° 45° 40° 36° 60° 90° 108° 120° 128. 6° 135° 140° 144° 2. These are exterior angles of regular polygons. How many sides does each polygon have? a. 24° 36° b. a) 10, 144°, 1440° 20° c. b)30° 12, 150°, 1800° c) 18, 160°, e. 2880° 12° d. d) 15, 156°, 2340° For each of the shapes: 5040° e) 30, 168°, What is the size of the interior angle? What is the sum of interior angles? Answers

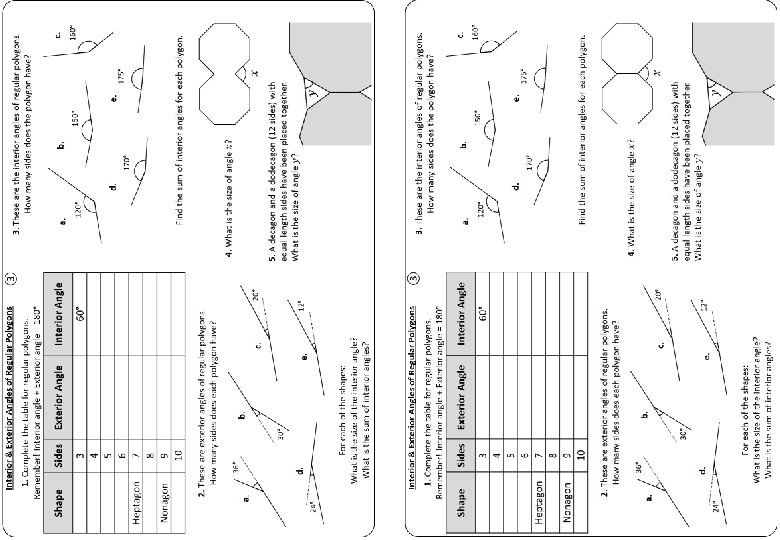
Interior & Exterior Angles of Regular Polygons ③ 1. Complete the table for regular polygons. Remember! Interior angle + Exterior angle = 180° Shape Sides Exterior Angle Interior Angle 3 4 5 6 7 8 9 10 Heptagon Nonagon e. 170° 175° Find the sum of interior angles for each polygon. b. c. 20° 30° 24° 160° 150° d. 36° d. c. b. a. 120° 60° 2. These are exterior angles of regular polygons. How many sides does each polygon have? a. 3. These are the interior angles of regular polygons. How many sides does the polygon have? e. For each of the shapes: What is the size of the interior angle? What is the sum of interior angles? 12°

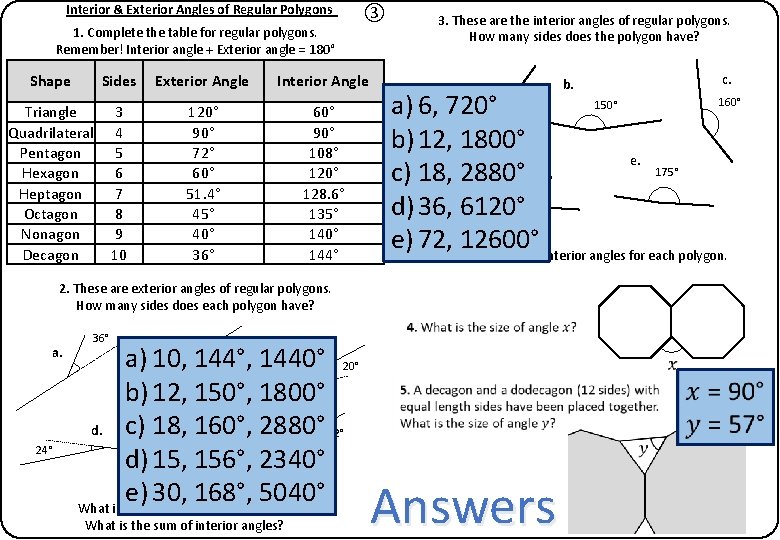
Interior & Exterior Angles of Regular Polygons ③ 1. Complete the table for regular polygons. Remember! Interior angle + Exterior angle = 180° Shape Sides Exterior Angle Interior Angle Triangle Quadrilateral Pentagon Hexagon Heptagon Octagon Nonagon Decagon 3 4 5 6 7 8 9 10 120° 90° 72° 60° 51. 4° 45° 40° 36° 60° 90° 108° 120° 128. 6° 135° 140° 144° 3. These are the interior angles of regular polygons. How many sides does the polygon have? a. 24° b. a) 10, 144°, 1440° 20° c. b)30° 12, 150°, 1800° c) 18, 160°, e. 2880° 12° d. d) 15, 156°, 2340° For each of the shapes: 5040° e) 30, 168°, What is the size of the interior angle? What is the sum of interior angles? c. 160° 150° 120° a) 6, 720° b) 12, 1800° d. e. 175° c) 18, 2880° 170° d) 36, 6120° e) 72, Find 12600° the sum of interior angles for each polygon. 2. These are exterior angles of regular polygons. How many sides does each polygon have? 36° b. Answers

KNOWLEDGE CHECK

KNOWLEDGE CHECK Interior angle of a regular octagon = 135° Exterior angle of a regular hexagon = 60°

Check your success! I can calculate the sum of interior angles of regular polygons. I can calculate interior and exterior angles of regular polygons. Using an exterior angle, I can calculate the number of sides of a regular polygon.

Check your success! I can calculate the sum of interior angles of regular polygons. I can calculate interior and exterior angles of regular polygons. Using an exterior angle, I can calculate the number of sides of a regular polygon.

Write a text message to a friend describing… Why exterior angles total 360°

Questions? Comments? Suggestions? …or have you found a mistake!? Any feedback would be appreciated . Please feel free to email: tom@goteachmaths. co. uk