Angles Learning Objectives G 3 apply the properties

Angles

Learning Objectives • G 3 apply the properties of angles at a point, angles at a point on a straight line, vertically opposite angles; understand use alternate and corresponding angles on parallel lines; derive and use the sum of angles in a triangle (e. g. to deduce and use the angle sum in any polygon, and to derive properties of regular polygons

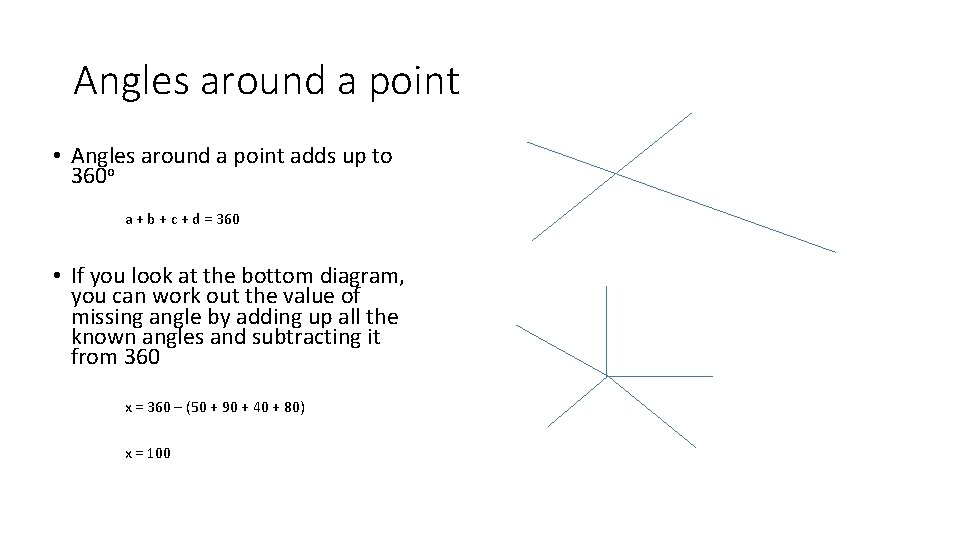
Angles around a point • Angles around a point adds up to 360 o a + b + c + d = 360 • If you look at the bottom diagram, you can work out the value of missing angle by adding up all the known angles and subtracting it from 360 x = 360 – (50 + 90 + 40 + 80) x = 100

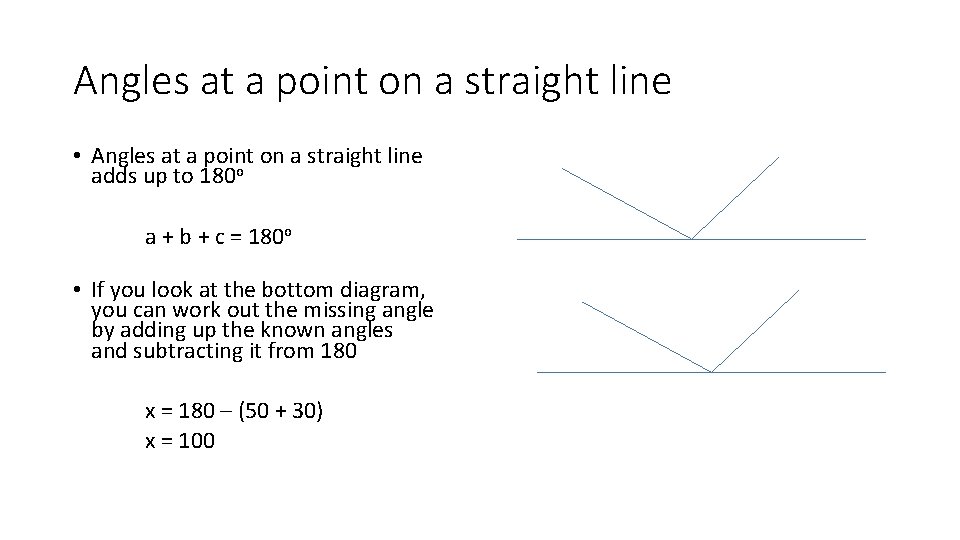
Angles at a point on a straight line • Angles at a point on a straight line adds up to 180 o a + b + c = 180 o • If you look at the bottom diagram, you can work out the missing angle by adding up the known angles and subtracting it from 180 x = 180 – (50 + 30) x = 100

Angles around a point and straight line - Practice Questions

Vertically Opposite and Alternate Angles When two lines intersects, two pairs of opposite angles are formed. Vertically opposite angles are equal When a straight line cross two parallel lines, it forms two pairs of alternate angles (it normally forms a Z shape). Alternate angles are equal

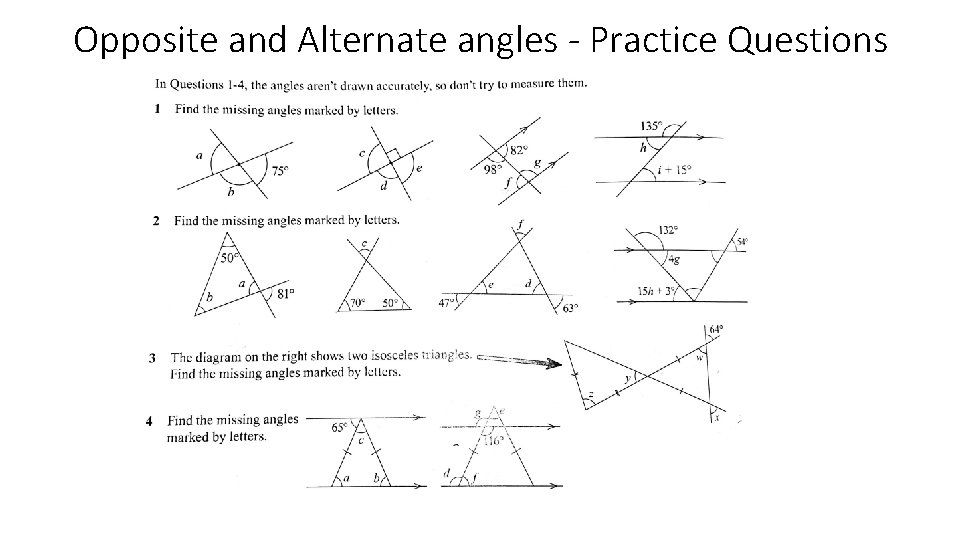
Opposite and Alternate angles - Practice Questions

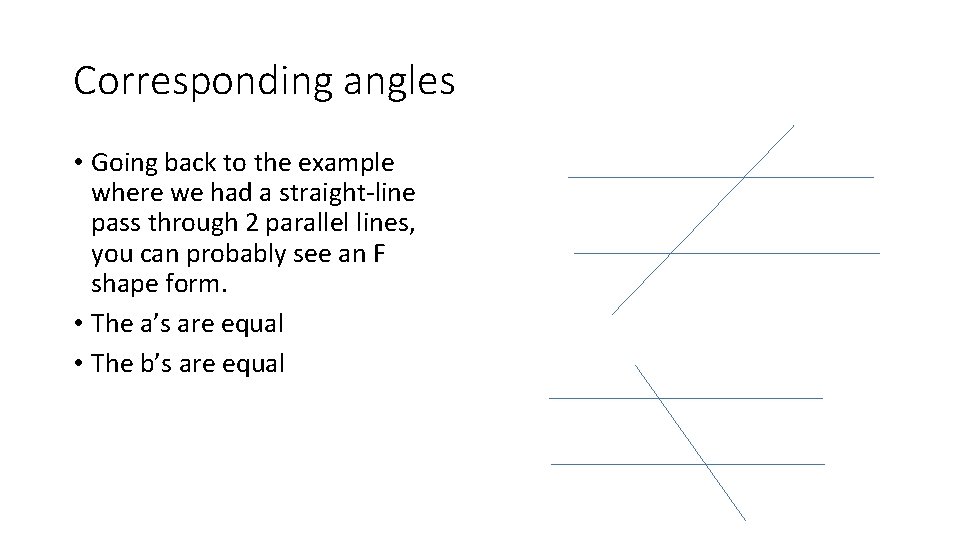
Corresponding angles • Going back to the example where we had a straight-line pass through 2 parallel lines, you can probably see an F shape form. • The a’s are equal • The b’s are equal

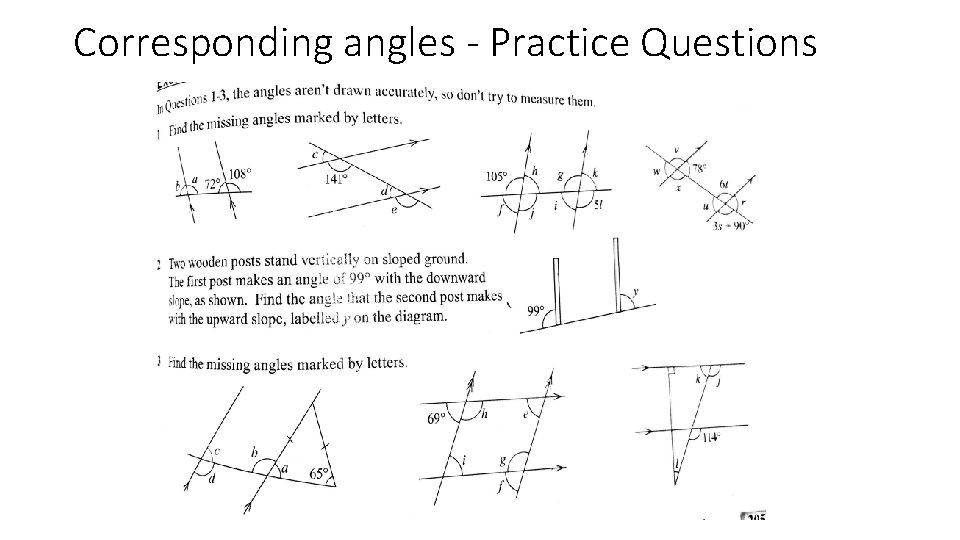
Corresponding angles - Practice Questions

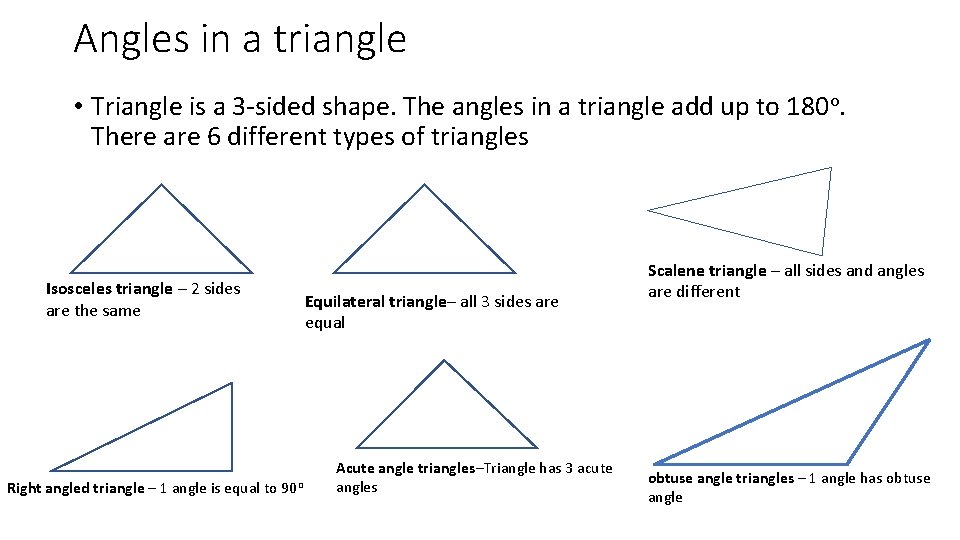
Angles in a triangle • Triangle is a 3 -sided shape. The angles in a triangle add up to 180 o. There are 6 different types of triangles Isosceles triangle – 2 sides are the same Right angled triangle – 1 angle is equal to Equilateral triangle– all 3 sides are equal 90 o Acute angle triangles–Triangle has 3 acute angles Scalene triangle – all sides and angles are different obtuse angle triangles – 1 angle has obtuse angle

Angles in a triangle - Practice Questions

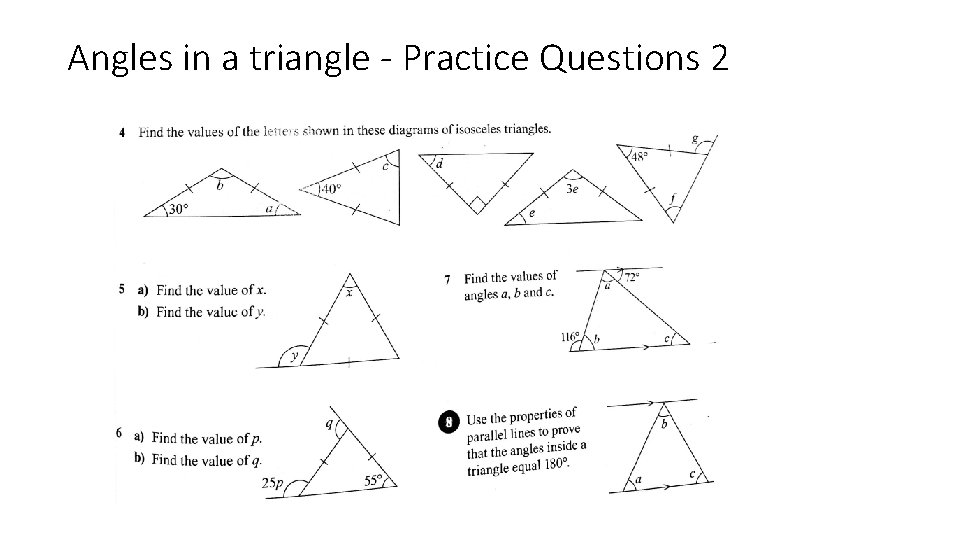
Angles in a triangle - Practice Questions 2

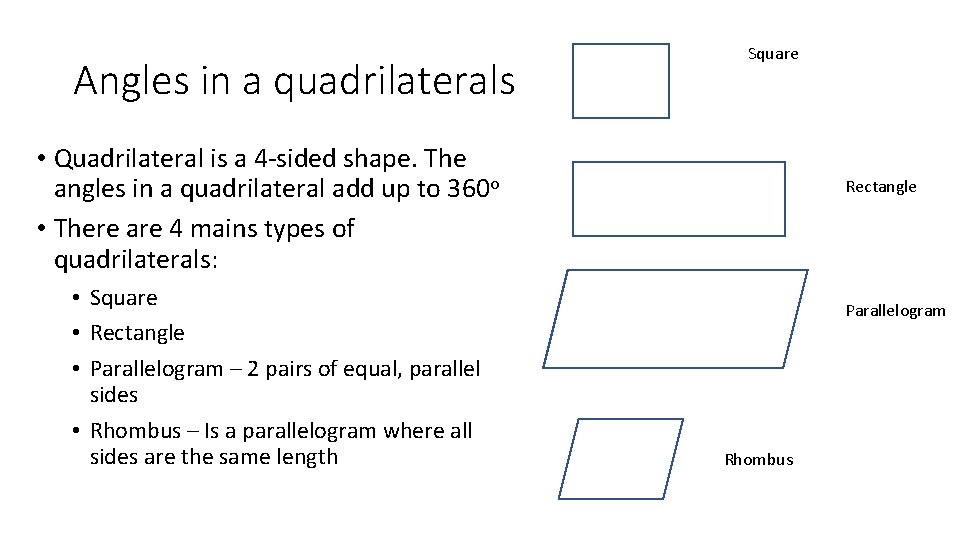
Angles in a quadrilaterals Square • Quadrilateral is a 4 -sided shape. The angles in a quadrilateral add up to 360 o • There are 4 mains types of quadrilaterals: • Square • Rectangle • Parallelogram – 2 pairs of equal, parallel sides • Rhombus – Is a parallelogram where all sides are the same length Rectangle Parallelogram Rhombus

Quadrilaterals - Practice Questions

Polygon • Polygon is a name given to a shape where all the lines are straight • Polygons have a special names depending on the number of sides they have: • • Triangle – 3 -sided shape Quadrilaterals – 4 -sided shape Pentagon – 5 -sided shape Hexagon – 6 -sided shape Heptagon – 7 -sided shape Octagon – 8 -sided shape Nonagon – 9 -sided shape Decagon – 310 -sided shape • A regular polygon is when all the sides and angles of a polygon is equal to each other

Interior angles of polygon • Interior angles of a polygon are the angles inside of a polygon. • To work out the sum of a polygon’s interior angle, you can use the formula below • S = (n – 2) x 180 o Where n is the number of sides • For example, the sum of interior angles of a pentagon is S = (n – 2) x 180 o S = (5 – 2) x 180 o S = 540 o This means, all the angles in a pentagon adds up to 540 o. If you want to find angle of each interior angle of a regular pentagon, simply divide 540 by 5 = 108 o

Interior angle - Practice Questions

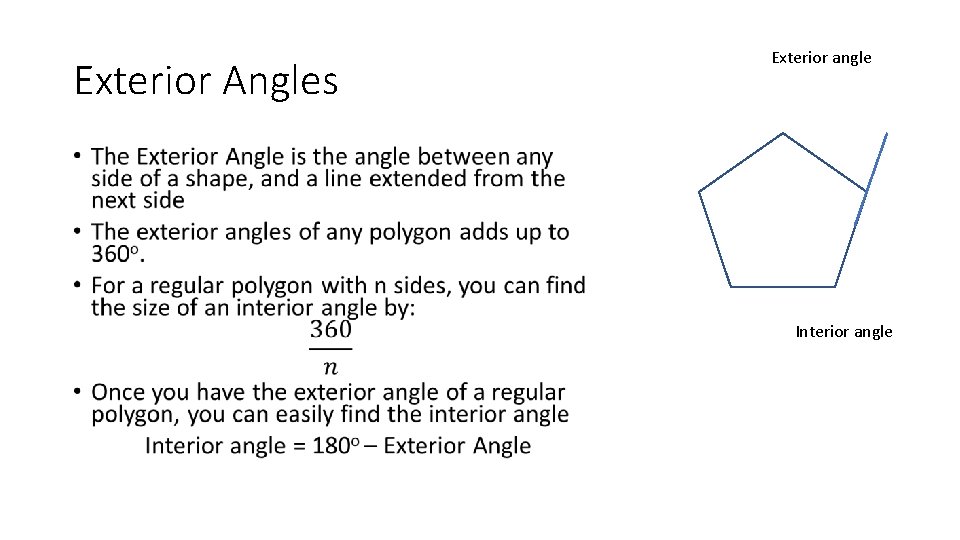
Exterior Angles Exterior angle • Interior angle

Exterior angle - Practice Questions

Exterior angle - Practice Questions 2

Exam style questions • https: //www. mathsgenie. co. uk/resources/2 -angles. pdf • https: //www. mathsgenie. co. uk/resources/4 -angles-in-parallellines. pdf • https: //www. mathsgenie. co. uk/resources/4 -angles-in-polygons. pdf